VI. Matière
Gaz parfaits
La loi des gaz parfaits, qui constitue la base de la thermodynamique, fut découverte expérimentalement au 19° siècle. Elle énonce qu'à température constante, si l'on diminue le volume alors la pression augmente :
P * V = N * kB * T
où N est le nombre de particules, et kB est la constante de Boltzmann.
Plus exactement, N est le nombre de moles du gaz (cf. infra #mole).
Afin de comprendre les mécanismes physiques de cette loi il faut prendre en compte la nature atomique (c-à-d non continue) de la matière. Étymologiquement le mot "gaz" vient du grec "chaos", ce qui traduit le fait que les particules qui le composent sont en mouvement permanent, provoquant ainsi des chocs sur les parois du récipient qui le contient. Ce mouvement permanent vient du fait que les atomes étant plongés dans le vide, ils ne subissent aucune force de frottement ⇒ ils conservent leur éventuel mouvement. L'idée vient alors de calculer la pression d'un gaz sur base des forces d'impact des particules sur les parois.
Ainsi la pression atmosphérique est la pression exercée par l'air sur les corps, vivants comme inertes.
Ce calcul est cependant extrêmement complexe, en raison du nombre de particules et de la diversité de leurs vitesses, directions et masses. La voie de simplification choisie par Maxwell et Boltzmann, les inventeurs de la théorie cinétique des gaz, est la physique statistique. Une voie encore plus simple, développée ici, est fondée sur la notion de force d'impact moyenne, appliquée au cas d'une expérience de la pensée.
Étape 1
On étudie d'abord le cas simplifié d'un volume de gaz (i) contenu dans un piston librement coulissant (pas de forces de frottement), et (ii) composé d'une seule particule en mouvement vertical d'allers-retours, et dont on connaît la masse et la vitesse. Comme d'autre part on introduit la gravitation dans l'expérience il en résulte que le piston a tendance à descendre.
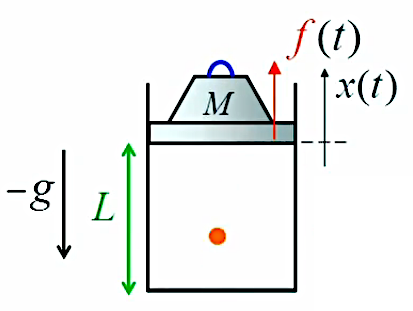
On veut alors identifier les conditions d'équilibre volumique de ce gaz, c-à-d telles que la force d'impact moyenne f– de cette particule contre le piston est égale au poids M * g de celui-ci, de sorte que ce gaz à une particule supporte le piston à une certaine hauteur. f– est donc une force imaginaire continue qui porte le piston comme si celui-ci reposait sur un socle (portage statique ≈ portage dynamique) :
f– = M * g
Cf. troisième loi de Newton ou principe "d'action-réaction" : toutes les forces apparaissent par couple de forces opposées.
Vu que g est connu il reste à déterminer M (puisque par hypothèse m et v sont connus).
Pour ce faire on recourt au principe selon lequel l'équilibre est caractérisé par la conservation des quantités de mouvement du piston (M*V) et du volume de gaz (m*v) :
M * V = m * v ⇔
NB : où m et v sont supposés connus.
M = m * v / V ⇒ il reste à déterminer V.
Or, soit x la position verticale du piston, on peut considérer que l'équilibre est caractérisé par xt=0 (la dynamique cyclique entre la particule et le piston est telle que celui-ci oscille autour d'une position xt=0) :
x = ( V * T ) - g / 2 * T2 = 0 (164) où V est la vitesse initiale du piston, et T le temps mis par la particule pour faire un aller-retour ⇔
V = g * T / 2 ⇒ il reste à déterminer T.
Or soit L la hauteur du volume de gaz :
v = 2 * L / T ⇔ T = 2 * L / v ⇒ substitué dans V :
V = g * L / v ⇒ substitué dans : M * V = m * v ⇒
M = m * v2 / g / L ⇔
M * g = m * v2 / L ⇔
f– = m * v2 / L
f– est ainsi déterminé puisque l'on connaît m, v et L. En outre on s'est affranchi de g dans son expression (ce qui est une bonne chose puisque les propriétés d'un gaz sont identiques en apesanteur ou à la surface de la Terre).
Si dans (188) on substitue L=T*v/2 ⇒
f– = M * g = 2 * m * v / T
qui exprime la condition d'équilibre du piston de masse M, autour d'une position d'équilibre, sous l'action de la quantité de mouvement m*v du gaz à particule unique.
On est alors en mesure de faire le lien avec la loi expérimentale grâce à Ec = m * v2 / 2 (185) que l'on substitue dans (191) ⇒
f– * L = 2 * Ec ⇒
Soit S la surface supérieure du cylindre :
( f– / S ) * ( L * S ) = 2 * Ec ⇔
P * V = 2 * Ec
qu'en comparant avec
P * V = N * kB * T
on pourrait qualifier de "loi des gaz parfaits à une particule". Il nous reste donc à généraliser au cas de N particules.
La comparaison des deux équations révèle également le lien entre énergie cinétique et température (le T de (187) est la température, et non pas la période traitée ci-avant).
Étape 2
On va maintenant généraliser les deux hypothèses principales de l'étape 1 : (i) on considère N particules, au lieu d'une seule ; (ii) leur direction est quelconque, et non plus uniquement verticale.
Nous raisonnons alors dans le cadre d'un gaz à l'équilibre tel que la force d'impact moyenne f– de ses particules contre chacune de ses parois est égale à la force de réaction exercée par celles-ci.
Pour ce faire on va poser comme hypothèse simplificatrice que ce gaz est parfait, c-à-d que ses particules constitutives (atomes ou molécules) n'interagissent pas entre elles (de sorte qu'elles n'interagissent qu'avec les parois du récipient), ce qui requiert :
de les considérer comme des "masses ponctuelles", c-à-d que leur volume étant (sous cette condition) d'un ordre de grandeur très inférieur à la distance moyenne qui les sépare, on considère qu'elles ne se rencontrent quasiment jamais (il n'y a donc pas d'interactions entre elles) ; on dit alors que le gaz qu'elles forment est "dilué", c-à-d que sa pression est faible ;
que sa température, et donc l'énergie cinétique et la vitesse de ses particules, ne soient pas trop basses, sans quoi il y aura des agrégats de particules c-à-d des interactions entre elles (et il ne s'agit alors plus d'un gaz parfait) : en effet si l'énergie cinétique est trop faible, alors elle sera insuffisante pour neutraliser les forces d'attractions électromagnétiques entres particules.
Il n'existe pas de gaz parfait, mais tout gaz peut se rapprocher des ces conditions de faible pression et température.
Les particules ponctuelles étant maintenant mobiles dans toutes les directions, il faut considérer leur vitesse non plus comme un simple scalaire mais comme un vecteur (cf. supra #vecteur).
f→(t) = m * dv→/dt
qui exprime les chocs sur la paroi et la subséquente modification de vitesse.
⇔ par (56) :
f→(t) = m * (dvx/dt * 1→x + dvy/dt * 1→y + dvz/dt * 1→z) ⇒
On fait alors une nouvelle hypothèse simplificatrice : on suppose que même à l'échelle microscopique la paroi est parfaitement lisse ⇒ deux des trois composantes cartésiennes de la vitesse sont inchangées lors des chocs contre une paroi (ce qui, en l'absence de cette hypothèse, est relativement vérifié en moyenne) ⇒ il n'y a que la composante perpendiculaire de la vitesse (disons vx) qui change lors d'un contact avec une paroi ⇒
f→(t) = m * dvx/dt * 1→x ⇔
f→(t), force d'impact moyenne d'une particule d'inclinaison quelconque, est donc orientée perpendiculairement à la paroi qui subit le choc.
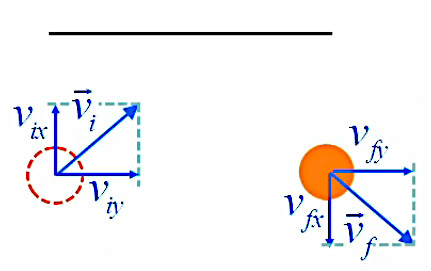
Bilan après le choc contre la paroi : viy = vfy
Dans l'étape théorique suivante les forces d'impact exercées par les N particules sur la paroi sont sommées en une force unique :
F = ∑n=1N f–n ⇒ par (188) :
F = ∑ m * vnx2 / L
⇔
F = N * m / L * ∑ vnx2 / N
⇔
F = N * m / L * < vx2 >
où < vx2 > est la moyenne "d'ensemble" (tandis que f– est une moyenne "temporelle") des vitesses en x.
Ensuite en raison de la distribution isotrope des vitesses (aucune des directions, donc aucune des composantes de la vitesse, n'est privilégiée puisqu'on se situe dans le vide) on a que :
< vx2 > = < vy2 > = < vz2 >
or par (51) :
∑ vn2 = ∑ vnx2 + ∑ vny2 + ∑ vny2
⇒ en divisant les deux membres par N :
< v2 > = 3 * < vx2 > ⇒
NB : 3 représente donc le nombre des dimensions de l'espace, c-à-d le nombre de liberté qu'on les particules de bouger.
F = N * m / L * < v2 > / 3 ⇔
en divisant par la surface S de la paroi supérieure :
P = N * m / V * < v2 > / 3 ⇔
P * V = N * 1/3 * m * < v2 > ⇒
si l'on compare avec l'égalité expérimentale
P * V = N * kB * T
on en déduit que
1/3 * m * < v2 > = kB * T ⇔
2 * < m * v2 / 2 > / 3 = kB * T
⇒ par (185) :
T = 2/3 * < Ec > / kB
où < Ec > est l'énergie cinétique moyenne par particule de gaz.
On comprend alors ce qu'est la température en termes physiques. On comprend en particulier pourquoi la température la plus basse qui puisse exister – le zéro absolu – est celle d'un gaz parfait dont l'énergie cinétique est nulle, niveau le plus bas que l'énergie cinétique puisse atteindre. On comprend également qu'en apportant de la chaleur à un gaz, donc en augmentant sa température, on augmente son énergie cinétique. On verra que l'énergie thermique est en fait de l'énergie cinétique (du moins pour les gaz monoatomiques).
Atomes
2. Isotopes
3. Tableau périodique
Modèle atomique
Un atome est une particule élémentaire de matière. On a recensé à ce jour environ 120 types d'atomes ("éléments"). Ils sont classés dans le tableau des éléments (cf. infra). On les représente physiquement sous forme d'une sphère (modèle atomique).
Nous verrons plus loin la différence entre "atome" et "élément" au travers de la notion d'atome isotope.
La taille d'un atome varie de 0,25 à 3 Å (un ångström vaut cent picomètres et 1 pm = 10 -10 m) selon le type de matière (hydrogène, carbone, etc). Ainsi la taille d'un atome (ordre de 10-10 m) par rapport à un pamplemousse est du même ordre de grandeur que la taille d'une sphère de 1cm de diamètre par rapport à la Terre.
Les atomes ne se distinguent pas que par leur taille, mais aussi (et surtout) par leur structure.
Dans le modèle atomique l'atome est composé de particules (dites "subatomiques") :
- un noyau, composé de deux types de "nucléons" :
- protons :
- charge électrique individuelle positive (1,602.10 -19 C = charge +1);
Le coulomb est la charge électrique (la quantité d'électricité) traversant une section d'un conducteur parcouru par un courant d'intensité de un ampère pendant une seconde (1 C = 1 A*s).
- masse individuelle = 1,673.10 -27 kg.
- charge électrique individuelle positive (1,602.10 -19 C = charge +1);
- neutrons
- sans charge électrique;
- masse individuelle = 1,675.10 -27 kg.
- protons :
- d'un nuage entourant le noyau et composé d'électrons, qui sont des particules :
- chargées négativement (charge -1);
- de masse individuelle = 9,109.10 -31 kg soit 1.838 fois moins lourde qu'un nucléon, de sorte qu'elle est souvent ignorée dans les calculs des chimistes (et comme les électrons sont environ deux fois moins nombreux que les nucléons il en résulte que le noyau est environ 4.000 fois plus lourd que son nuage).
Quel que soit le type d'atome, les protons ont donc la même masse, de même que les neutrons.
| Charge | Masse | |
|---|---|---|
| p + | +1 | 1 |
| n 0 | 0 | 1 |
| e - | -1 | négligeable |
La masse d'un atome est donc concentrée dans le noyau (99,97%), tandis que sa charge est répartie, entre protons du noyau et nuage électronique. La concentration de masse est encore plus impressionnante lorsque l'on se rend compte que le rapport entre la taille du noyau et celle de l'atome est équivalent à celui entre la tête d'une fourmi et un terrain de football (ordre de grandeur du rapport : 1/100.000).
Taille (ordre de grandeur)
| Atome | 10-10 m |
|---|---|
| Noyau | 10-15 m |
Unités de
mesure
Dès lors que la masse d'un proton est très proche de celle d'un neutron, on a simplifié la mesure en posant que la masse d'un nucléon (proton ou neutron) – notée mu – vaut une "unité de masse atomique" (notée u ou u.m.a.), dont la valeur est déterminée comme suit :
jusqu'en 2019 sa valeur était mesurée, en prenant comme référentiel l'atome isotope 12C (le plus fréquent des trois types d'atome de carbone : cf. infra pour la notion d'isotope) ; comme celui-ci comporte 12 nucléons (6 protons + 6 neutrons) on a donc que l'unité de masse atomique vaut un douzième de la masse de 12C :
mu ≈ 1 u ≡ m12C / 12 =
1,66053 8921 * 10 -27 kgdepuis 2019, l'unité de masse atomique n'est plus mesurée mais fixée par convention :
mu ≈ 1 u ≡ 1 / NA g =
1,66053 9066 * 10 -27 kg
où NA est le nombre d'Avogadro : au 19° siècle le physicien et chimiste turinois Avogadro avait démontré que deux volumes égaux de gaz différents, dans les mêmes conditions de température et de pression, contiennent un nombre identique de molécules ⇒ on en a déduit que 1g de n'importe quelle matière contient le même nombre NA de nucléons ; pour s'accorder sur une valeur précises de NA les scientifiques ont convenu :- jusqu'en 2019, que NA est le nombre d'atomes de carbone dans 12 grammes de carbone 12, soit 6,022140 86 * 1023 ;
- depuis 2019, que dorénavant la valeur de NA ne serait plus mesurée mais fixée par convention à NA ≡ N(1g) = 6,022140 76 * 1023
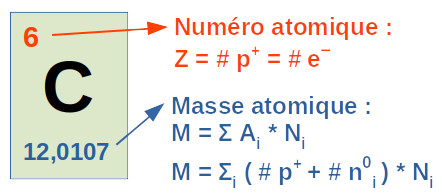
Mais ce qui caractérise essentiellement un type d'atome c'est le nombre de protons qu'il contient (exemple : le carbone est l'atome composé de six protons), appelé numéro atomique (noté Z, et annoté comme suit 6C, pour le carbone). NB : la matière est généralement neutre c-à-d que la charge électrique d'un atome est nulle ⇒ Z indique donc également le nombre d'électrons (#protons = #électrons).
Quant au nombre de nucléons (protons et neutrons) on l'appelle nombre de masse (noté A).
En résumé :
- Numéro atomique : Z = # p+ = # e‒
- Nombre de masse : A = # p+ + # n0
Le nombre de masse permet de calculer la masse atomique (exprimée en u). Mais pour cela il convient d'introduire la notion d'isotopes.
Isotopes
Sur base des définitions que nous venons d'énoncer, on pourrait s'attendre à ce qu'un atome de carbone pèse A u = 12 u. Or un atome de carbone pèse 12,01074 u [ on le sait en mesurant la masse d'une mole de carbone, qui vaut 12,01074 g (cf. infra #mole) ]. La raison en est qu'il existe différents types d'atomes, qui diffèrent par leur nombre de neutrons, et donc par leur masse : ce sont les isotopes de l'atome. Ainsi lorsque l'on pèse une certaine quantité d'un atome on pèsera un mélange de ces trois isotopes. La proportion de chaque isotope est appelée "abondance naturelle" (notée Ni) de l'isotope.
Par exemple pour le carbone on a : N(12C)≈98,93% ; N(13C)≈1,07% ; N(14C)≈0%. Et dans ce cas on constate bien que :
M(C) = ∑i Ai * Ni
⇒
M(C) = A(12C) * N(12C) + A(13C) * N(13C)+ A(14C) * N(14C) ⇔
M(C) ≈ ( 6 + 6 ) * 0,9893 + ( 6 + 7 ) * 0,0107 + ( 6 + 8 ) * 0 = 12,0107.
Il est important de bien comprendre que :
- la masse atomique est donc une moyenne pondérée des nombres de masse.
- quand l'unité de la masse atomique M(X) n'est pas spécifiée, on convient qu'il s'agit de l'unité de masse atomique "u" (190), et non de grammes ou de kilos !
Tableau périodique
Dans chaque case du tableau des éléments (cf. ci-dessous) le chiffre situé au-dessus du symbole de l'élément est son numéro atomique tandis que le nombre situé en dessous du symbole est la masse atomique (cf. supra #isotopes). Le tableau "périodique" peut se lire notamment de gauche à droite c-à-d dans l'ordre des numéros atomiques. Les "périodes" sont les lignes, tandis qu'à chaque colonne est attribué un numéro de groupe (ainsi par exemple les éléments du groupe IA réagissent de façon assez semblable aux élément du groupe IB). Dix familles d'éléments sont ainsi regroupées par couleurs.
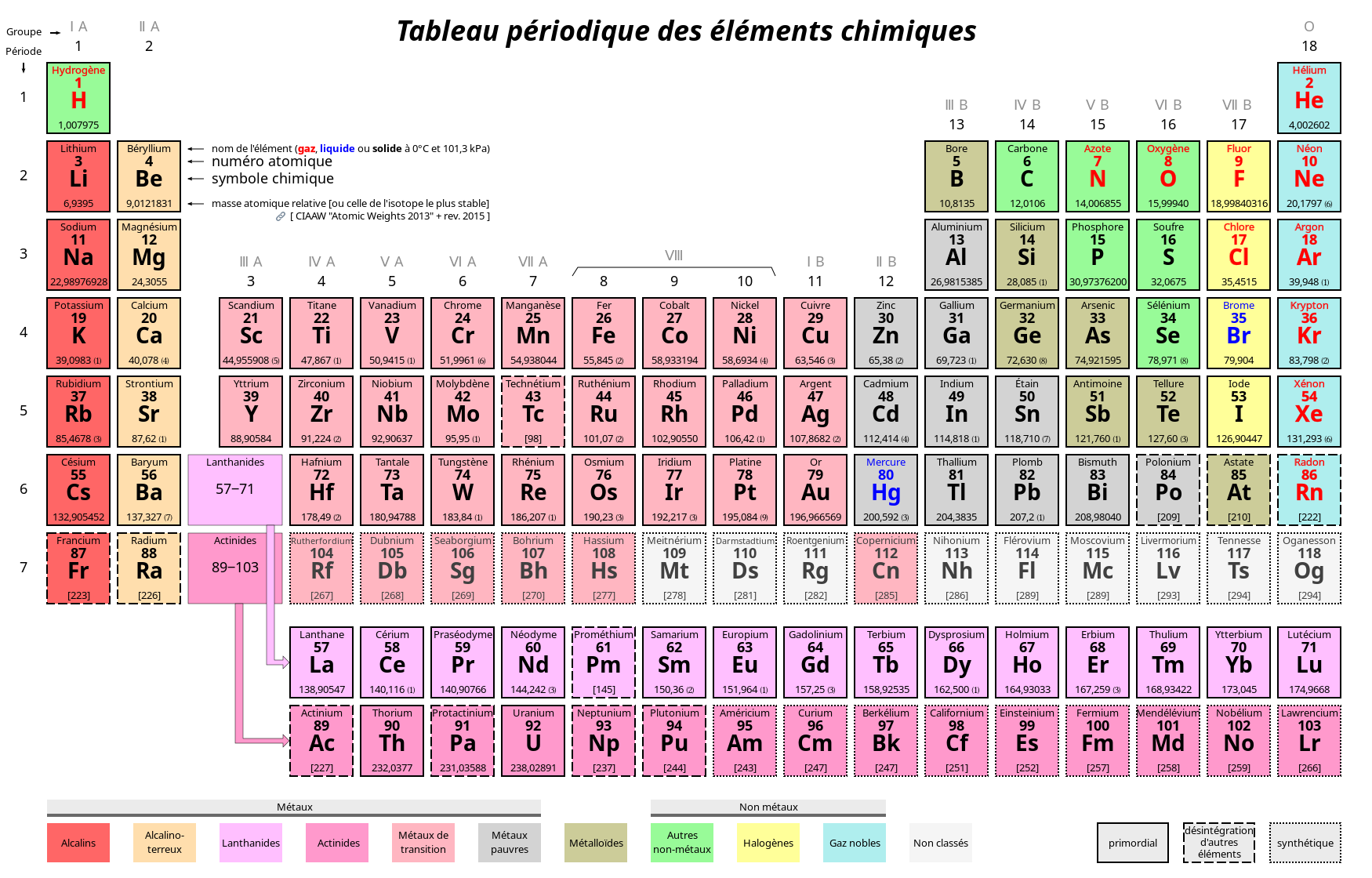
Pour agrandir : clic droit sur l'image > Afficher > cliquer sur l'image pour agrandir au maximum.
L'atome d'hydrogène (H) est le premier élément du tableau périodique (cf. infra) : c'est l'atome le plus petit, simple et léger : il est composé d'un seul proton, d'un seul électron et ne possède pas de neutron.
Description succincte des familles d'éléments :
- métaux alcalins (Li, Na, K, Rb, Cs, Fr) : réagissent fortement avec l'oxygène de l'air et de l'eau;
- halogènes (F, Cl, Br, I) : gaz diatomiques, et toxiques car il réagissent fortement (avec notamment les métaux alcalins);
- alcalino-terreux (Be, Mg, Ca, Sr, Ba, Ra) : il font les mêmes types de composés que les alcalins mais avec des taux de combinaison doubles;
- métaux de transition (Ti, Cr, Fe, Ni, Cu, Zn, Ag, Pt (catalyseur), Cd, Au, ...) : solides, conducteurs, ductiles, à haute température de fusion/ébullition, combinables entre eux (alliages), composables avec les non-métaux (oxydes, chlorures, sulfates, ...) en proportions diverses (exemple d'oxydes de fer : FeO, Fe2O3, F3O4) ;
- gaz nobles ou rares, inertes (He, Ne, Ar, Kr, Xe, Rn) : monoatomiques, très peu réactifs (ce qui en fait de bon gaz parfait) --> ils forment peu de composés (d'où leur nom de inertes ou nobles);
- non métaux (C, H, O, N, P, S) : jouent un rôle déterminant dans le métabolisme des organismes vivants, légers (faible masse atomique), combinables (acides aminés – Ala, Tyr, ... – constituant les protéines, molécules de phospholipides constituant les membranes cellulaires, molécules d'ADN, ...);
- métalloïdes (B, Si, Ge, As, Sb, Te, At) : moins bons conducteurs que les métaux (⇒ utilisés pour fabriquer des semi-conducteurs, transistors et circuits intégrés);
- métaux pauvres (Al, Ga, Sn, Pb, ...);
- lanthanides ou "terres rares" (La, Pr, Nd, ...);
- actinides (U, Pu, Md, ...) : les plus lourds, matières premières des centrales nucléaires.
Les éléments récemment découverts sont les plus lourds : ils contiennent le plus grand nombre de protons. Découvrir de nouveaux éléments requiert de plus en plus d'énergie ⇒ au fur et à mesure que nous pourrons mobiliser de plus grandes quantités d'énergie grâce au progrès technologique découvrirons-nous sans fin de nouveaux éléments ?
Masse et débit volumiques
• Débit volumique
La masse volumique ρ est la masse par unité de volume :
ρ = M / V
Ainsi la masse volumique du bois de pin (0,45 kg/dm3) est inférieure à la masse volumique de l'eau (1 kg/dm3 = 1 g/cm3 = 1 t/m3... par convention !). Grâce au tableau périodique des éléments (cf. infra #atomes) la comparaison de la masse atomique de l'aluminium et du plomb permet de donner l'explication atomique de la masse volumique. Ainsi le noyau du plomb contient dix fois plus de nucléons (270/27). Ce rapport est supérieur à celui des masses volumiques(11,4/2,7≈4,2) car les atomes de plomb sont plus volumineux.
De même la masse volumique de l'eau est inférieure à celle de l'aluminium car les molécules qui la composent sont plus volumineuses que les atomes d'Al tout en ayant moins de nucléons.
Maintenant comparons l'air à l'eau. L'air est composé de molécules d'oxygène (O2) et d'azote (N2) qui contiennent respectivement 32 et 28 nucléons. La molécule d'eau (H2O) comporte 2*1+16=18 nucléons. Pourtant l'air est manifestement plus léger que l'eau (sa masse volumique est inférieure : 1,3 g/dm3). La raison en est que les molécules d'oxygène et d'azote ne sont pas compactes (pas liées par des forces électriques) ⇔ il y en a moins par unité de volume. En effet l'air est un gaz.
La masse volumique est sensible à l'hétérogénéité du matériaux (exemple masse volumique de l'emmental) --> dans ce cas la masse volumique doit être considérée comme une grandeur moyenne. À l'extrême la masse volumique d'une machine n'a pas beaucoup de sens.
Enfin la masse volumique ne doit pas être confondue avec la densité, qui est, pour un même volume, le rapport entre la masse du matériaux et celle d'un matériaux de référence. Les volumes étant identiques la densité est donc le rapport des masse volumiques.
Commençons par rappeler ces grandeurs volumiques et massique standards : un litre représente un volume de 1.000 cm3 soit le volume d'un cube d'arrête de 10cm (⇒ 1 ml = 1 cm3), et un litre d'eau pèse 1kg.
Il importe de distinguer débit volumique DV = V / t et débit massique DM = M / t.
Débit volumique. Une autre façon, tout aussi intuitive, de formuler le débit volumique est :
DV = S * v
où S est la surface de la section du conduit, et v la vitesse du fluide dans ce conduit.
Démonstration :
DV = V / t ⇔
DV = S * L / t
par définition de la vitesse v = L / t
DV = S * v * t / t ⇒
DV = S * v
CQFD
Le débit massique peut se calculer à partir de la masse volumique ρ = M / V (193) :
DM = M / t = ρ * V / t.
Relation. On peut alors démontrer que DM = ρ * DV :
DM = ρ * V / t =
ρ * S * L / t =
ρ * S * v =
par (188) :
ρ * DV
CQFD
N.B. On notera le lien intuitif entre M = ρ * V et DM = ρ * DV
Chimie
2. Mole
3. Solution et concentration
4. Énergie et cinetique
Réaction chimique
Il est théoriquement possible de transmuter la matière, par exemple le plomb (82Pb) en or (79Au) : pour cela il faut enlever 82-79=3 protons à chaque atome de plomb. Cependant cela requiert tellement d'énergie que dans l'état actuel des technologies la transmutation est plus coûteuse que l'extraction.
Cette anecdote est l'occasion de préciser que le champ de la physique nucléaire se situe à l'échelle intra-atomique, qui est par nature plus petite que l'échelle inter-atomique de la chimie, dont le champ est le nuage électronique qui entoure le noyau des atomes (la biologie, ou plus exactement la biochimie, se situant quant à elle à une échelle encore plus grande : celle des molécules, qui sont des ensemble d'atomes).
Il en résulte qu'une réaction nucléaire est une transformation d'un ou plusieurs noyaux atomiques, de sorte qu'elle transforme un élément en un autre. Tandis qu'une réaction chimique ne concerne que les électrons ou les liaisons entre les atomes, donc conserve les éléments, mais transforme leurs composés que sont les molécules.
Une réaction chimique est un phénomène de transformation de la matière, que l'on observe dans certains cas lorsque l'on mélange des substances. Les composés se transforment ainsi en un ou plusieurs composés d'une autre nature (c-à-d avec des propriétés physico-chimiques différentes), cela tout en conservant la quantité de matière (N.d.A : cf. premier et second principes de la thermodynamique). Les réactions chimiques se distinguent notamment par leur intensité (on utilise parfois le terme de "violence") : ainsi par exemple lorsque l'on jette un morceau de sodium dans un récipient contenant de l'eau, le morceau de sodium se met à bouger en dégageant de la fumée, puis il brûle et enfin explose.
Autres exemples. Les organismes vivants sont le lieu de nombreuses et permanentes réactions chimiques, qui déterminent le métabolisme de ces organismes : respiration, nutrition, ... (cf. infra #metabolisme). Les réactions chimiques sont abondamment utilisées dans l'industrie, notamment pour produire des métaux à partir de minerais, ou encore des polymères (matières plastiques telles que le nylon). Elles sont également utiles pour le recyclage de déchets (cf. les stations d'épuration). Enfin nous sommes tous des chimistes, puisque l'art culinaire consiste en l'exploitation de réactions chimiques sur des aliments (exemple : réaction de maillard).
Revenons à la réaction de la vidéo, et écrivons son équation chimique :
Réactifs --> Produits
Na + H2O --> NaOH + H2
On constate que l'atome de sodium (Na) prend la place d'un des deux atomes d'hydrogène (H), qui est éjecté, ce qui produit une molécule d'hydroxyde de sodium et une molécule de dihydrogène (gaz). Cependant l'équation ci-dessus n'est pas correcte car le principe de conservation de la matière/énergie ("rien ne se perd, rien ne se créé") n'est pas respecté : on a plus d'atomes de H en produits (à droite de la flèche) qu'en réactifs (à gauche de la flèche) ⇒ il faut diviser la molécule de dioxygène par 2 :
Na + H2O --> NaOH + 1/2 * H2
mais comme dans la réalité il n'existe pas de "demi-molécule" il faut alors multiplier les deux membres par 2 afin d'équilibrer correctement l'équation :
2Na + 2H2O --> 2NaOH + H2
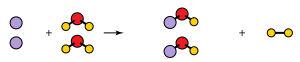
Mole
Les nombres situés à gauche des réactifs et produits de la section ci-dessus sont appelés "coefficients stœchiométriques". Ils constituent la base de la chimie quantitative. Celle-ci repose sur la notion de mole, qui exprime une relation entre la masse d'une certaine quantité de matière et le nombre d'atomes qu'elle contient. La notion de mole permet ainsi de quantifier correctement les réactifs d'une réaction chimique.
La mole est « la quantité de matière d'un système contenant exactement NA (nombre d'Avogadro) entités élémentaires (atomes, ions, molécules, etc.), et est telle que une mole de nucléons (protons et neutrons), c-à-d NA nucléons, pèse 1g ». Autrement dit, 1g de n'importe quelle matière contient 1 mole de nucléons :
NA * mu = 1 [g/mol]
où :
• mu : masse du nucléon (proton ou neutron) (190) ;
• NA : nombre d'Avogadro (191).
PS : on note l'unité [g/mol] au lieu de [g] pour préciser qu'il s'agit de la masse d'une mole.
La définition de "une mole de nucléons" (196) n'est donc qu'une reformulation de la définition de la masse du nucléon (mu), où 1g de n'importe quelle matière est exprimé comme correspondant à la masse du nucléon multipliée par NA .
Ainsi (196) permet d'associer une quantité de substance (membre de droite) à un nombre de nucléons (membre de gauche) et donc à un nombre d'atomes ou molécules.
Pour bien comprendre l'utilité de cette notion de mole, revenons à celle de masse atomique. Nous avons vu que la masse d'un atome est représentée à plus de 99% par celle du noyau. Par conséquent la masse d'un atome X vaut approximativement le produit du nombre de nucléons (c-à-d le nombre de masse AX) par la masse d'un nucléon (mu) :
mX ≈ mnoyau X = AX * mu [g]
⇔ en unités u :
mX = AX [u]
Cependant nous avons vu que ce raisonnement est trop simpliste. Il faut prendre en compte les isotopes : la masse d'un atome X est une moyenne pondérée de ses isotopes, notée Mx (192), et est mentionnée dans le tableau périodique des éléments (cf. supra #tableau-periodique). Par conséquent il faut réécrire les équations ci-dessus comme suit :
mX = MX [u] = MX * mu [g]
Notons que (197) vaut quelle que soit l'entité chimique X considérée : atome ou molécule. Ainsi la masse d'un atome de carbone (C) vaut 12 [u], et la masse d'une molécule d'H2O vaut 2*1+16=18[u].
Ensuite, à partir d'une "entité" (atome ou molécule), on définit sa masse molaire (masse d'une mole) en substituant mu de (196) dans (197) ⇒
entité : mX = MX / Na [g] ⇒
mole : NA * mX = MX [g/mol]
Ainsi par exemple la masse d'une mole de carbone (C) vaut 12g/mol, et celle d'une mole de H2O vaut [(2*1)+16]=18g/mol.
On notera qu'une "entité" de X (atome de C, molécule H2O, ...) pèse MX [u] (197), tandis qu'une mole de X pèse MX [g] (198).
Enfin, à partir de la masse molaire (198) on pourra calculer le nombre nX de moles de matière X contenues dans une masse qX de cette matière, en divisant celle-ci par la masse molaire MX :
nX = qX / MX
Appliquons maintenant ces principes de chimie quantitative à notre équation chimique de la section précédente :
- NA * mNa = 23g : une mole de Na pèse environ 23g;
- NA * mH2O = 18g : une mole de H2O pèse 2*1+16=18g
- NA * mNaOH = 40g : une mole de NaOH pèse 23+16+1=40g
- NA * mH2 = 2g : une mole de H2 pèse 2*1=2g
On peut associer coefficients stœchiométriques et nombre de moles d'une réaction :
| 2Na | + | 2H2O | ⇒ | 2NaOH | + | H2 |
| ⇒ en multipliant les deux membres par NA (ne pas confondre avec Na) : | ||||||
| 2 moles Na | + | 2 moles H2O | ⇒ | 2 moles NaOH | + | 1 mole H2 |
Ne pas confondre Na (sodium) et NA (nombre d'Avogadro).
De sorte qu'à partir de n'importe quelle quantité de Na (par exemple 46g) on peut alors déterminer celles des autres réactifs et produits correspondant à l'équation.
| 2Na | + | 2H2O | ⇒ | 2NaOH | + | H2 |
| 2 moles Na | + | 2 moles H2O | ⇒ | 2 moles NaOH | + | 1 mole O2 |
| 46g | + | 36g | ⇒ | 80g | + | 2g |
On constate que 46+36=80+2. Ainsi la masse de matière est conservée (tout comme le nombre d'atomes).
On peut également déduire que :
18g de H2O contient 1 mole de H2O ⇒
1g de H2O contient 1/18 mole de H2O = 0,055 mole de H2O = 0,055 * NA molécules de H2O.
Solution et concentration
Certaines matière se mélangent facilement (mélange homogène) et d'autres pas (mélange hétérogène). Ainsi du sable et de l'eau donneront (même après agitation) deux "phases" : solide (sable) et liquide (eau). Même type de résultat si l'on remplace le sable par de l'huile (on parlera alors plutôt de phases "organique" pour l'huile, et "aqueuse" pour l'eau).
Mais si l'on remplace l'huile par du lait, on obtient alors un mélange homogène, ... du moins à l'oeil nu. Le lait, à l'instar de la peinture, est en réalité un colloïde (du grec "kollôdês" signifiant "collant") c-à-d une suspension d'une ou plusieurs substances dispersée(s) régulièrement dans un liquide, formant un système à phases séparées mais sans que cela soit visible à l'oeil nu.
En fait la distinction entre produits miscibles ou non n'est généralement pas dichotomique mais plutôt en continuum. L'homogénéité peut être approchée par agitation ou encore ajout d'un émulsifiant, de sorte que l'on obtient un mélange appelé "émulsion" : vinaigre+huile (mayonnaise) ou encore air+graisse (mousse).
Lorsque le mélange est homogène au niveau moléculaire on parle de solution. C'est le cas de l'eau et du sel (NaCl) : l'image ci-contre montre que les ions Na+ et Cl- (solutés) sont entourés de molécules de H2O (solvant).
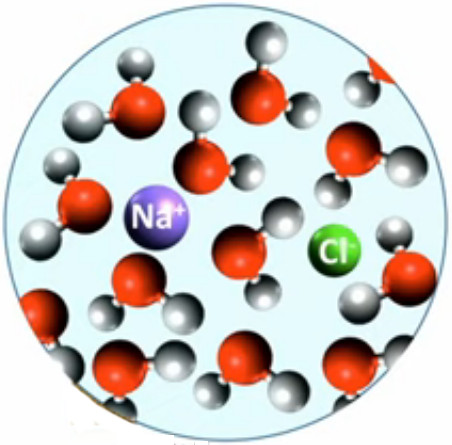
Dans le cas de solutions on peut alors considérer la concentration du soluté dans le solvant, par le rapport cc = quantité de soluté / volume de solvant
L'intérêt de la notion de concentration (cc) est qu'elle est indépendante de la quantité : une portion quelconque de solution a la même concentration que la solution puisque par nature la solution est spatialement homogène. La concentration est ainsi qualifiée de variable "intensive", à l'instar de la masse volumique ρ = M / V (193).
La cc se définit globalement par cc = quantité de soluté / volume de solvant. Mais on peut distinguer divers types d'indice selon la façon dont est mesuré le numérateur, c-à-d la quantité de soluté : masse, # moles, volume.
Concentration massique : Cm = masse soluté / volume solution [kg/m3 ou g/l]
Cependant du point de vue de l'analyse chimique on obtient plus d'informations en mesurant la quantité de soluté par le nombre de moles (et partant le nombre d'atomes) plutôt que par la masse :
Concentration molaire : CM = # moles / volume solution [mol/m3 ou mol/l]
On note parfois C ou [formuleMolécule] au lieu de CM
Calculons la cc molaire de 3g de NaCl dans 40ml de H2O :
CM = # molesNaCl / 0,04 ⇔ par (199) :
CM = mNaCl / MNaCl / 0,04 ⇔ par (198) :
CM = 3g / ( 23 + 35 ) / 0,04 = 1,3 mol/l
N.B. On voit que :
cc molaire = cc massique / masse molaire :
Démonstration :
CM = # moles / volume solution ⇔
CM = masse soluté / M / volume solution ⇔
CM = Cm / M
où M est la masse molaire (198).
Pourcentage en solution : volume de soluté / volume solution, comme dans le cas des boissons alcoolisées ("degrés" d'alcool).
Effets
La cc joue donc sur l'intensité d'une solution, et partant sur diverses propriétés telle que la couleur. Ainsi la couleur des pétales d'une plante est fonction de l'intensité de ses pigments, laquelle dépend de l'acidité (le "ph") du sol (qui vaut de 0-1 pour les acides forts à 13-14 pour une "base" (le contraire d'un acide). Et le ph est lui-même une variable intensive puisqu'il vaut le négatif de la cc en ion H3O+ : ph = -log[H3O+].
Une autre propriété déterminée par la cc est la vitesse de réaction entre deux solutés d'un solvant : plus leur cc est élevée, plus la probabilité de rencontre entre leurs particules est élevée, et partant la vitesse de réaction de l'ensemble du soluté mixte.
Énergie et cinétique chimique
Énergie
Dans la réaction illustrée par la vidéo supra, ce n'est pas le sodium "qui a brûlé" (cf. vidéo) : la réaction produit du dihydrogène H2 qui réagit à son tour avec l'oxygène de l'atmosphère, en provoquant ainsi une réaction de combustion. Cette réaction chimique est donc associée à un dégagement d'énergie sous forme de chaleur, on parle alors de réaction exothermique :
2H2 + O2 --> 2H2O (+ énergie)N.d.A. : sauf in vitro, une réaction chimique entraîne généralement d'autres réactions chimiques.
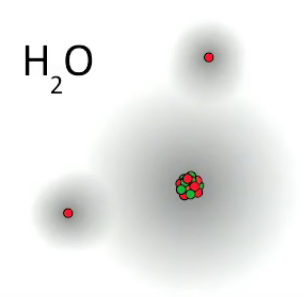
Dans une molécule chaque liaison entre atomes se fait par mise en commun d'un électron. Chaque liaison, ou plus exactement chaque électron de la liaison peut-être vu comme détenteur d'une sorte d'énergie potentielle (cf. supra #energie-potentielle). Ainsi par exemple dans la réaction de synthèse de l'eau, une molécule de dihydrogène vient briser le lien qui unit les deux atomes du dioxyde, cela libère une énergie qui propulse la molécule de H2O synthétisée. La réaction de combustion correspond à une émission d'énergie (thermique et mécanique), de sorte que le produit d'une réaction exothermique correspond à un état énergétique inférieur à celui des réactifs, en vertu du principe de conservation.
Le graphique ci-dessous représente l'évolution du bilan énergétique d'une réaction. On voit que le pic correspondant à l'énergie d'activation peut-être abaissé, grâce à un catalyseur. Par exemple en ajoutant de la mousse de platine aux réactifs H2 et O2 on pourra déclencher la réaction avec seulement une échauffement plutôt qu'une explosion (la réaction est donc plus lente).
Le graphe ci-dessous est celui d'une réaction exothermique : l'énergie d'activation (c-à-d requise pour briser les liaisons dans les réactifs) est inférieure à l'énergie de réaction (c-à-d dégagée par la formation des liaisons chimiques dans les produits de réaction).
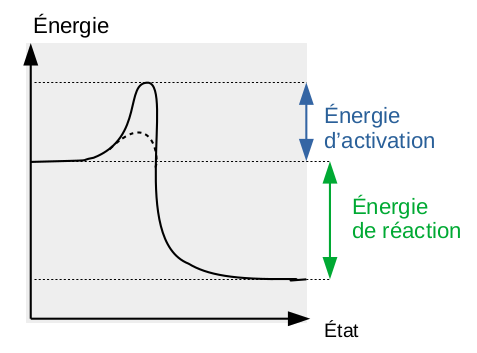
Réaction exothermique
La combustion est une réaction exothermique (NB : la réaction de combustion peut prendre des formes très subtiles, telles que la respiration).
Le graphe ci-dessous est celui d'une réaction exothermique : l'énergie d'activation (c-à-d requise pour briser les liaisons dans les réactifs) est supérieure à l'énergie de réaction (c-à-d dégagée par la formation des liaisons chimiques dans les produits de réaction).
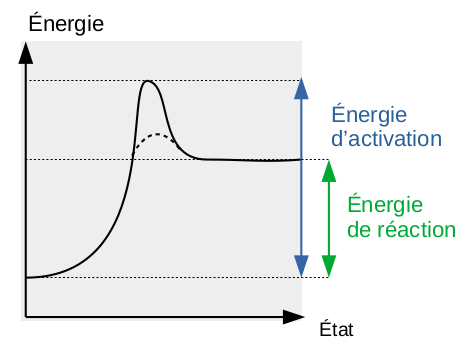
Réaction endothermique
La glace qui fond est une réaction exothermique.
Les notions d'énergie d'activation et de réaction endothermique illustrent le fait qu'il ne suffit pas toujours de mélanger des réactifs pour que la réaction se déclenche. Un apport d'énergie (électricité dans l'eau, flamme dans l'air, ...) peut être nécessaire. Ainsi en fournissant de l'énergie on pourra provoquer une réaction chimique inverse.
Par exemple, à l'inverse de la réaction exothermique (201), on peut produire du H2 et du O2 à partir de H2O. Pour ce faire une technique est l'électrolyse de l'eau, qui est une réaction endothermique :
2H2O (+ énergie) --> 2H2 + O2
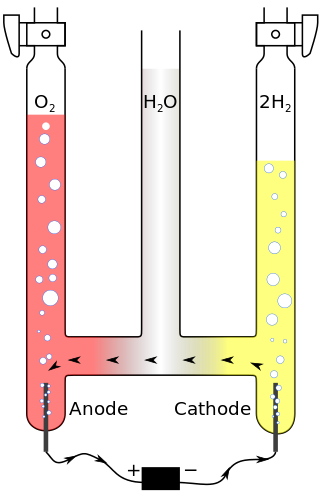
Électrolyse de l'eau
Le schéma ci-contre montre qu'en créant un courant électrique dans le système, on provoque une production de gaz dans les deux colonnes, et telle que le volume de gaz produit dans la colonne de droite est le double de celui de la colonne de gauche, ce qui correspond au rapport des coefficients stoechométriques du membre de droite : la réaction produit deux fois plus de molécules de H2 que de O2.
Cinétique
On voit que les réactions chimique se distinguent notament par leur vitesse : dans une explosion la réaction est quasiment immédiate tandis que dans d'autres phénomènes elle est beaucoup plus lente (par exemple la rouille sur un métal).
Cette observation nous conduit à la question : quel est le mécanisme d'une réaction chimique ? Elle se fait par le biais des électrons c-à-d des forces électromagnétiques. Et contrairement à la dynamique orbitale régulière des astres cosmiques (régie par la force gravitationnelle), les mouvements des électrons autour du noyau semblent chaotiques (aléatoires), de sorte qu'on ne parle pas d'orbites mais de probabilité de présence.
Une réaction chimique consiste dans la mise en commun d'électrons, ce qui requiert des chocs entre les atomes des réactifs (dans le cas de la dernière équation supra il faut que trois molécules se rencontrent : deux de H2 et une de O2). Or la probabilité de ces chocs diminue avec le nombre d'atome par unité volumique (concentration, pression) ainsi qu'avec l'agitation de ces atomes (liée à la température). D'autre part on pourrait penser qu'une réaction chimique requiert également un positionnement ad hoc des atomes, ainsi qu'une mobilisation efficace de l'énergie nécessaire. Mais comme tout cela est statistiquement peu probable de se produire simultanément il faut donc trouver une autre explication. C'est ce qu'ont fait les prix Nobel de chimie 1956 Hinshelwood & Semenov. Dans leur théorie les molécules sont d'abord cassées en leur "radicaux libres" qui, possédant sur leur couche externe un ou plusieurs électrons non appariés, sont généralement instables et réagissent fortement avec les autres réactifs (avec nouvelles productions de radicaux), provoquant de complexes réactions en chaînes ⇒ l'explosion de la vidéo.
On peut ainsi distinguer :
- thermodynamique chimique ⇔ notion de bilan énergétique : dans quel sens se produit la réaction ?
- cinétique chimique ⇔ notion de vitesse de réaction : pas de réaction < réaction modérée < explosion.
Cohésion électromagnétique
2. Orbites électroniques
3. Liaison covalente
Algèbre de l'électricité
Lors du big bang, une quantité phénoménale d'énergie a été libérée, ainsi que des neutrons. Ces particules élémentaires n'ont apparemment pas d'autre propriété que leur masse (leur charge électrique est nulle) ... du moins pendant une quinzaine de minutes, après lesquelles elles se mettent à vibrer puis émettent un électron (particule de charge négative), ce qui transforme le neutron en proton (particule de charge positive), et fait apparaître entre les deux particules une force d'attraction, dite "électrique". Sous certains aspects, celle-ci est comparable à la force de gravitation (force d'attraction entre tous les corps de masses significatives) : réciprocité de la force d'attraction entre les deux corps, intensité de cette force en fonction de la distance entre les corps. Mais elle est aussi beaucoup plus forte (facteur 1040 !) et plus complexe : la force électrique est attractive entre proton et électron, mais répulsive entre entre particules semblables (protons ou électrons).
L'attribution d'une charge positive au proton et négative à l'électron, plutôt que le contraire, n'est qu'une convention mathématique permettant de modéliser, au moyen d'une "algèbre de l'électricité", la détermination du sens des forces d'attraction et de répulsion observées entre particules : + = répulsion ; - = attraction ; - * + = - ; - * - = + ; + * + = +.

Ok, les types différents s'attirent. Mais qui va vers l'autre ? Réponse : tout est question de conventions ...
Au moyen de cet algèbre de l'électricité nous allons pouvoir étudier et formaliser la dynamique des forces intra-atomiques (c-à-d à l'intérieur des atomes) et inter-atomiques (c-à-d entre atomes) : en particulier les forces de cohésion et les orbites électroniques.
N.d.A. Il s'agit ici de l'approche purement mathématique. Au niveau physique c'est plus complexe. Ainsi l'effectuation de la force d'attraction n'est pas symétrique : ce sera plutôt l'électron qui se rapproche du proton, car la masse de ce dernier étant nettement plus élevée, son inertie l'est également. Ceci dit, le résultat est le même ...
Orbites électroniques
Lorsqu'un proton et un électron se rencontrent deux options sont possibles : soit ils forment un neutron, soit ils forment un atome d'hydrogène (le plus simple des atomes : 1 proton et 1 électron).
Forces électrique (attractive) et gravitationnelles ont un autre point commun : combinées avec une force centrifuge (en sens opposé, selon la loi d'action-réaction (169) ), elle provoquent un mouvement orbital (à une vitesse beaucoup plus grande dans le cas de la force électrique – de l'ordre du millions de m/s – que dans celui de la lune). Ainsi le système atomique composé d'un proton et d'un électron se déplaçant en orbite autour de son noyau (ici composé d'un seul proton et d'aucun neutron) est appelé "atome d'hydrogène" (noté H).
Le schéma suivant montre que lorsque deux atomes d'hydrogène sont suffisamment proches, ils peuvent être liés si la combinaison spatiale est telle que les forces d'attraction l'emporte sur les forces de répulsion. Dans ce cas ils vont alors former une molécule de dihydrogène (H2).
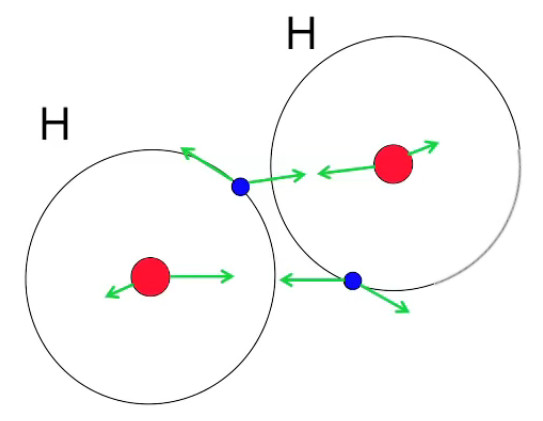
Dans cette nouvelle molécule les vecteurs d'attraction entre particules de signes différents sont toujours plus longs que les vecteurs de répulsion entre particules de mêmes signes. Et d'autre part la force d'attraction résultante est compensée par la force centrifuge de sens opposé, ce qui maintient la structure orbital des électrons dans un système atomique à deux noyaux (ici molécule H2).
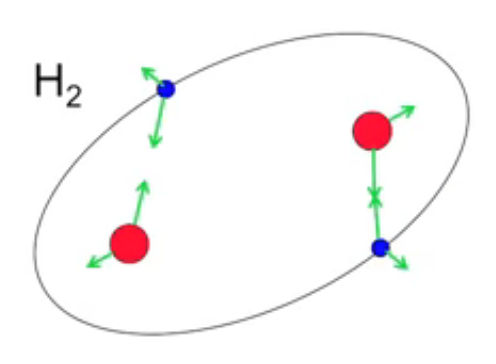
Molécule d'hydrogène, composée de deux atomes d'hydrogène, donc de deux protons (en rouge) et deux électrons (en bleu).
À l'échelle supérieure des interactions inter-moléculaires la force d'attraction entre molécules de dihydrogène est faible dans les conditions physico-chimiques de la surface de la Terre : des molécules de H2 qui entrent en collision ne provoquent généralement pas de réaction chimique. Cette absence d'interaction entre molécules fait de H2 ce que l'on appelle un "gaz".
Plasma
Les étoiles sont originellement des amas de gaz H2 dont la masse est tellement élevée que la force gravitationnelle devient supérieure aux forces électriques qui structurent chaque molécule de H2, de sorte que ces molécules sont brisées en protons et électrons. Cette "soupe" est appelée "plasma". Les mouvements de ces particules y sont permanents. Des neutrons sont alors formés par la rencontre de protons avec des électrons, et quand un neutron rencontre un proton on obtient un corps stable.
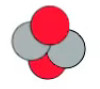
Lorsque ceux-ci collisionnent entre eux on obtient alors des corps à deux protons et deux neutrons où les neutrons jouent le rôle de "colle" entre les protons. Cette effet de colle joué par les neutrons est appelé "force nucléaire", ou encore "interaction forte" car elle est beaucoup plus forte que la force électrique qui repousse les deux protons entre eux. Ainsi dans l'image ci-contre la force de répulsion entre les deux protons (rouge, charges +) est plus que compensée par l'attraction de la force nucléaire exercée par les neutrons (gris, charges 0).
Des paquets de protons+neutrons de tailles différentes sont ainsi formés. Lorsqu'ils se trouvent à la surface de ces immenses corps célestes que sont les étoiles, ils sont alors dans des conditions physico-chimiques de plus faible pression et température (cette dernière n'étant plus que de quelques milliers de degrés) de sorte que des orbites électroniques sont possibles. Ainsi à l'amas de deux protons et deux neutrons de l'image précédente peuvent se lier en orbite deux électrons, de sorte que l'ensemble de ce système stable forme un atome d'hélium (He).
Par le même type de processus apparaissent tous les autres atomes repris dans le tableau périodique : des corps stables contenant des quantités différentes de protons et neutrons sont formés selon le même procédé que pour l'hélium, le nombre d'électrons (signe -) apparaissant étant égal à celui des protons (signe +). Ces électrons sont positionnés en couches composées de 2 électrons pour la première (la plus proche du noyau) et 8 par couche supplémentaire, sauf la dernière qui contient un nombre d'électrons inférieur ou égal à huit.
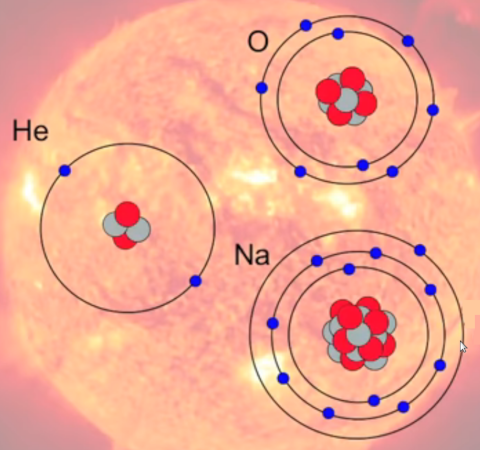
Neutrons en gris et protons en rouge. L'image ne peut représenter tous les nucléons (protons et neutrons) ainsi on peut constater dans le tableau périodique que l'atome d'oxygène contient 8 protons et l'atome de Na en contient 11.
Les étoiles sont donc des "fabriques à atomes" (cf. supra le #tableau-periodique des éléments).
Affinons notre compréhension de la dynamique des forces électromagnétiques et nucléaires. Plus un noyau est lourd, plus il a d'électrons (puisque la stabilité de l'atome requiert #protons=#électrons) ⇒ plus il y a d'orbites, moins forte est la force d'attraction du noyau sur les électrons des orbites plus éloignées (alors que ceux-ci sont repoussés par les électrons de la couche précédente). Ces électrons instables vont faciliter les réactions chimiques avec d'autres atomes.
Ions
Si l'on prend par exemple deux atomes Na et Cl on constate que la dernière couche du Na ne contient que 11-2-8=1 électron et va avoir tendance à le perdre lorsqu'il rentre en contact avec un atome tel que Cl dont la couche extérieure contient 17-2-8=7 électrons (notion d'affinité électronique qui est fonction du nombre d'électrons en couche externe et de la distance entre celle-ci et le noyau). L'atome Na devient donc un ion Na+ tandis que l'atome Cl devient un ion Cl – (un atome est neutre tandis qu'un ion a une charge électrique non neutre). Étant de signes opposés ces ions Na+ et Cl – vont alors s'attirer, et ainsi former des amas à structure symétrique que l'on appelle des cristaux (exemple : le sel NaCl).
D'autre part on comparera utilement la formation de la molécule de NaCl avec celle de H2O. Dans ce dernier cas il n'y a pas transfert mais mise en commun d'électrons de deux atomes d'H avec une atome d'O de sorte que la dernière couche orbitale de l'atome d'oxygène (8-2=6) est complétée à 8.
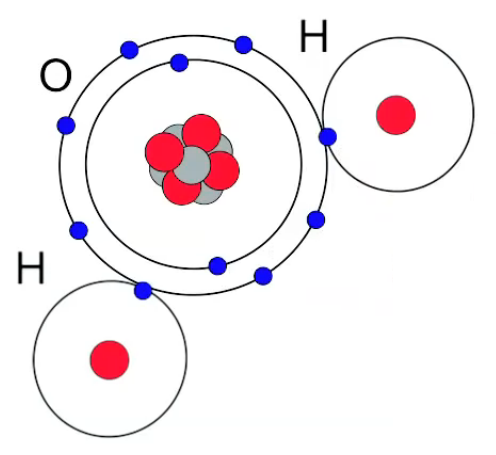
H2O : interaction intra-moléculaire.
Au niveau des interactions inter-moléculaires, on peut considérer chaque atome H d'une molécule H2O comme chargé 1+, et l'atome O de cette molécule comme chargé 2+. Ainsi l'image ci-contre montre que l'atome H d'une molécule H2O est attiré par un atome O d'une autre molécule H2O (on parle de "liaison hydrogène"). Mais cette attraction est relativement faible, ce qui fait de H2O un liquide (dans des conditions de température ni trop élevée ⇒ vapeur, ni trop basse ⇒ glace). De même cette attraction inter-moléculaire est forte chez les solides et quasiment inexistante chez les gaz.
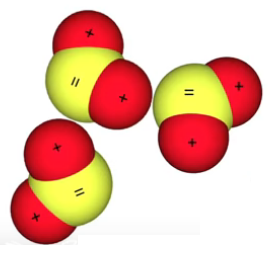
H2O : interaction inter-moléculaire. NB : "=" signifie "2-".
Dans le cas de la molécule de silice SiO2 la force d'attraction intermoléculaire est beaucoup plus forte, il s'agit d'un solide, qui le sera d'autant plus si dans les interstices viennent s'imbriquer des atomes de calcium, formant ainsi des silicates (roches, grains de sables, ...).
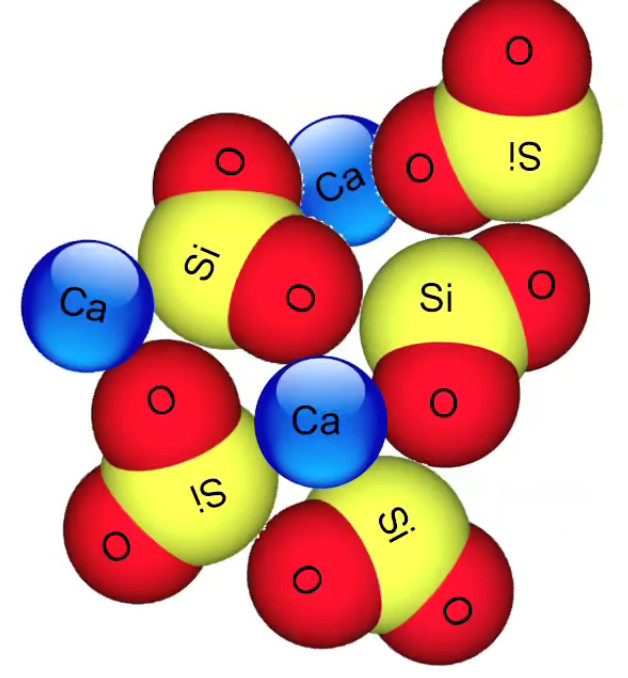
Les interactions électriques sont également à la base des grandes et complexes molécules organiques, composées de C, O, H, N, ..., telles que l'ADN, molécule composée de milliards d'atomes, et contenant le code génétique des organismes vivants. Le nombre de combinaisons possibles est quasiment infini.
Enin les phospholipides sont des molécules en forme de "tête" avec deux "queues", celles-ci forment des chaînes avec d'autres molécules de phospholipides, constituant ainsi les membranes cellulaires. Les têtes peuvent s'emboîter les unes avec les autres, formant ainsi des êtres pluricellulaires. Tout cela par l'effet des forces d'attraction électriques.
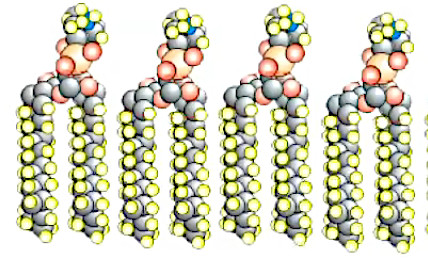
La force électrique est donc à la base de la vie.
Liaison covalente
Des atomes identiques ou différents peuvent former des molécules en se liant par partage de deux électrons libres de leur couche externe (appelée "couche de valence"). Ce doublet d'électrons joue donc le rôle de "colle", appelée liaison covalente. Plus un atome disposent d'électrons libres, plus il est à même de faire des liaisons covalentes avec d'autres atomes.
La règle de l'octet permet de déterminer le nombre d'électrons libres. Les atomes avec un numéro atomique Z ≥ 4 tendent à se combiner de façon à avoir huit électrons dans leur couche de valence (ce qui leur donne la même structure électronique qu'un gaz noble). N.d.A. : ainsi # e- libres = 8 - ( numéro atomique - # e- des couches inférieures) (PS : nous verrons plus loin qu'il existe des exceptions à cette règle).
-
Oxygène (O). Son numéro atomique est 8 (cf. supra #atomes) ⇒ # e- libres = 8 - ( 8 - 2 ) = 2 électrons libres. Il peut ainsi faire deux liaisons covalentes simples (exemple : H2O) ou une liaison covalente double (exemple : O2).
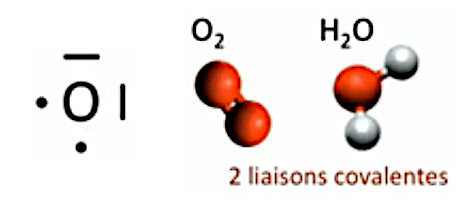
Azote (N). Son numéro atomique est 7 ⇒ # e- libres = 8 - ( 7 - 2 ) = 3 électrons libres. Il peut ainsi faire trois liaisons simples (exemple : NH3 appelé "ammoniac") ou une liaison triple (exemple : N2).
Carbone (C). Son numéro atomique est 6 ⇒ # e- libres = 8 - ( 6 - 2 ) = 4 électrons libres. Il peut ainsi faire quatre liaisons simples (exemple : CH4 appelé "méthane"). Lorsque toutes ses liaisons simples sont avec d'autres atomes de carbone, il forme un cristal de carbone, un des matériaux les plus solide qui soit (il ne fond qu'aux températures les plus élevées), dont un type célèbre est le "diamant".
Les liaisons permettent de nombreuses combinaisons en formant diverses chaînes atomiques. Partons ainsi du C5H12 (pentane) où les deux atomes de carbone externes de la chaîne sont liés à trois hydrogènes tandis que chacun des atomes de carbone internes est alors lié à 4-2=2 hydrogènes (cf. image ci-contre).
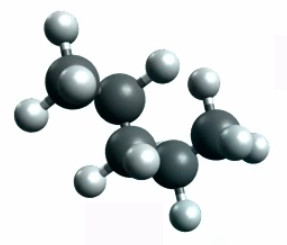
Pentane (C5H12) : deux des douze atomes H ne sont pas visibles car représentation 3D.
Si à partir du pentane ci-dessus on transforme les second et quatrième carbones de telle sorte qu'ils forment avec le carbone qui les précède une liaison double, on aura automatiquement 2*2=4 atomes H en moins ⇒ on obtient du C5H8 (pentadiène). Il y a ainsi modification de la composition et de la géométrie de la molécule, ce qui implique généralement une modification de ses propriétés physico-chimiques. En l'occurrence, alors que le pentane C5H12 est dit "saturé" (en H), car on a associé aux atomes de C le maximum possible d'atomes H, le pentadiène C5H8 est quant à lui "insaturé".
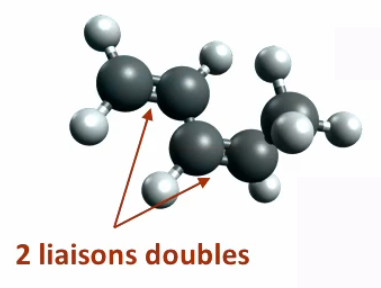
Pentadiène (C5H8).
Si, toujours à partir du pentane C5H12, on referme celui-ci en une boucle, il faudra pour cela retirer un atome H au deux carbones externes ⇒ on obtient du C5H10 (cyclo-pentane). Et à cette nouvelle configuration de la composition et de la géométrie de la molécule, correspondent de nouvelles propriétés physico-chimiques.
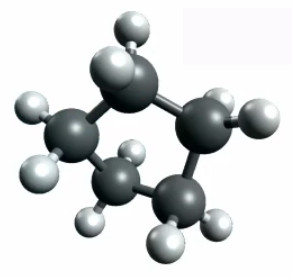
Cyclopentane (C5H10).
Fonctions
Pour modifier les propriétés physico-chimiques d'une molécule on peut également lui ajouter une "fonction", en lui ajoutant un atome de nouveau type. Prenons ainsi le cas de l'éthane (C2H6) : si l'on place un oxygène entre un hydrogène et son carbone, on obtient alors de l'éthanol (C2H5OH). En l'occurrence on obtient une "fonction alcool" (OH).
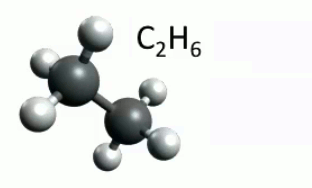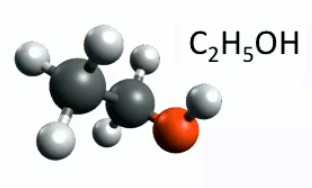
Animation : ajout d'une fonction alcool.
On peut aussi obtenir de l'alcool à partir de sucre au moyen de levures. D'autres bactéries peuvent à leur tour transformer l'alcool C2H5OH en acide éthanoïque (ou acétique) CH3COOH (vinaigre) : les deux H du carbone voisin du O sont remplacés par un liaison double avec un autre C ⇒ On a ainsi transformé la "fonction alcool" (OH) en "fonction acide carboxylique" (COOH).
Bactéries et levures sont des micro-organismes vivants (encore appelés microbes). La notion d'organisme vivant sera développée plus loin (#la-vie).
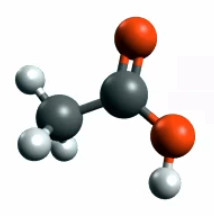
Acide éthanoïque (ou acétique) CH3COOH.
On peut ajouter plusieurs fonctions. Par exemple si, partant de l'acide éthanoïque ci-dessus on remplace un des trois H du C externe de la chaîne, par un azote (qui est lié à deux H puisque l'azote a trois électrons libres) ⇒ on ajoute ainsi une "fonction amine" (NH2), qui donne de la glycine NH2CH2COOH. La combinaison de fonctions acide et amine est appelée fonction "acide aminé". Les acides aminés sont une des "briques de base" pour fabriquer des protéines (macromolécules constitutives des cellules vivantes).
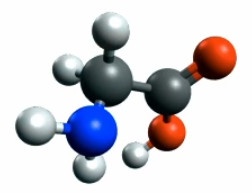
Glycine NH2CH2COOH.
Ainsi les doubles liaisons, les cycles (boucles), les ramifications et les fonctions ouvrent la porte à une nombre immense de combinaisons possibles d'atomes et de molécules.
Cohésion nucléaire
• Datation au carbone 14
La théorie électromagnétique permet d'expliquer la dynamique des force inter-atomiques, c-à-d entre atomes. Nous verrons infra que sa formulation est F(r) = kC * q1 * q2 / r 2 (202), où q1 et q2 sont deux charges électriques, r la distance qui les sépare, et kC une constante universelle.
Mais pour ce qui concerne la cohésion intra-atomique c-à-d entre particules constitutives du noyau atomique (protons + et neutrons 0), la théorie électromagnétique n'est plus suffisante puisque, étant de même signe, les protons se repoussent. Or les atomes sont généralement stables. Les physiciens ont donc été conduits à en conclure qu'au niveau du noyau atomique intervient une autre force, plus forte que la force électrique. C'est la force attractive, dite "nucléaire".
Nous allons voir que celle-ci est une force par laquelle les neutrons jouent le rôle de "colle" entre les protons du noyau atomique (nous verrons plus loin que l'on considère en pratique deux types de force nucléaire : forte et faible). Sa formulation est nettement plus complexe que celle de la force électromagnétique (elle fait appel à la mécanique quantique), et est encore l'objet de propositions diverses, dont un exemple est l'équation de Klein-Gordon (dont le développement sort du cadre de cette publication) :
N.d.A. La fonction d'onde Ψ(r,t) exprime la position d'une particule à la position r et à l'instant t. Elle est telle que Ψ( r →, t ) = < r | Ψ(t) > qui exprime que ... (à faire).
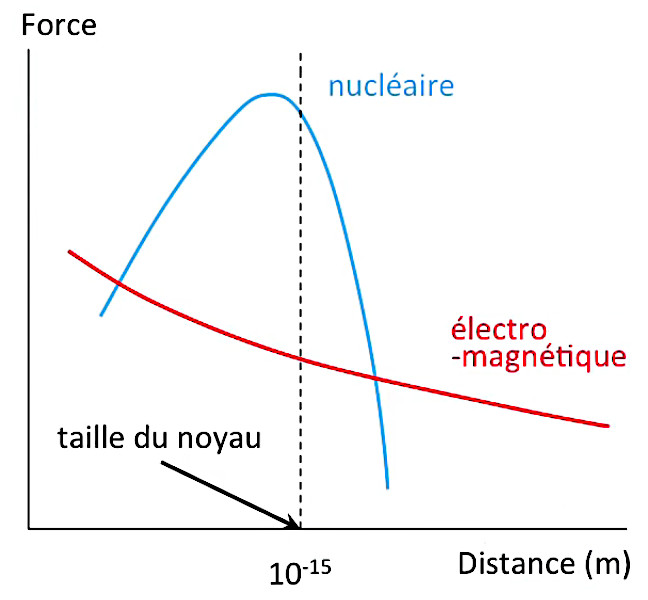
Le graphique ci-dessous illustre le fait qu'à l'échelle de taille du noyau atomique (10-15 m), la force nucléaire est nettement plus puissante que la force électromagnétique.
Le schéma suivant exprime le nombre de neutrons d'un atome en fonction de son nombre de protons (c-à-d son numéro atomique Z). Il montre donc le nombre d'isotopes (cf. supra #isotopes) de chaque atome (isotopes également appelé "nucléides" lorsqu'on les caractérise en outre par leur état d'énergie nucléaire).
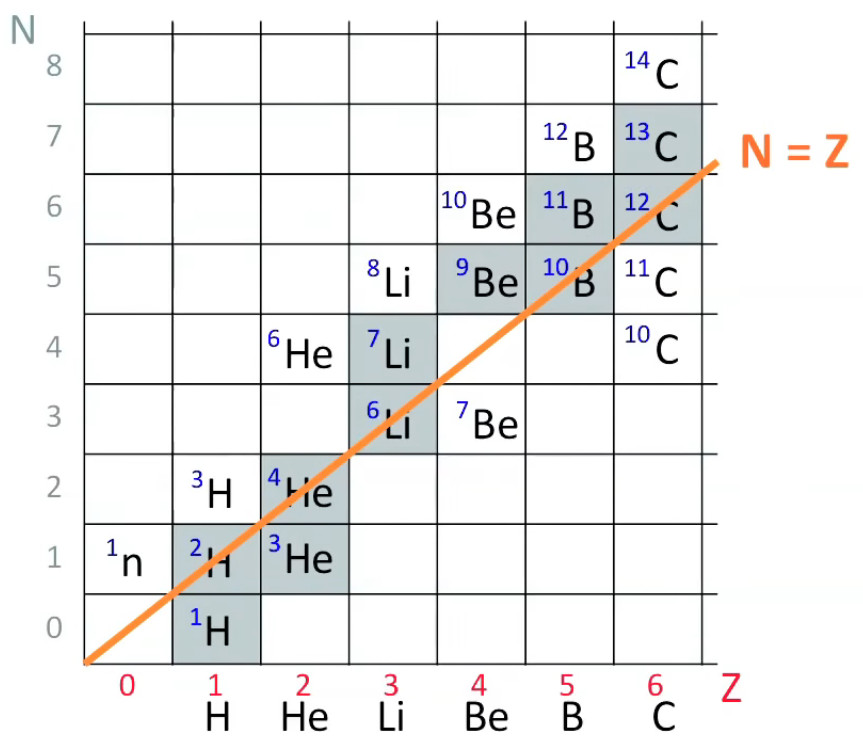
Notons qu'outres les isotopes naturels, d'autres isotopes peuvent être créés au moyen d'un accélérateur de particules (cf. infra #accelerateur-particule). Les cases intermédiaires vides, telles que la case (2,3), correspondent à des isotopes fugaces c-à-d qui disparaissent très vite. Les cases grises correspondent aux isotopes les plus stables, qui sont généralement les isotopes naturels. Les isotopes mentionnés en cases blanches constituent une classe intermédiaire d'isotopes dits "instables".
On constate dans ce graphique que les isotopes naturels (cases grises) sont les plus proches de la diagonales c-à-d qu'ils ont généralement un nombre de neutrons proche de leur nombre de protons. Cela est cohérent avec le fait que la force nucléaire est plus forte entre nucléons différents (proton-neutron) qu'entre nucléons identiques (proton-proton, neutron-neutron).
N.d.A. Autrement dit : FN = kN * / ( #protons - #neutrons ) ⇒ la force de cohésion nucléaire est d'autant plus forte que #protons - #neutrons est petit c-à-d que #neutrons est proche de #protons.
Cependant le graphique ci-contre montre que cette propriété selon laquelle les isotopes les plus stables sont ceux avec un même nombre de protons et neutrons est de moins en moins vraie au fur et à mesure qu'augmentent le nombre de protons, et partant la masse atomique.
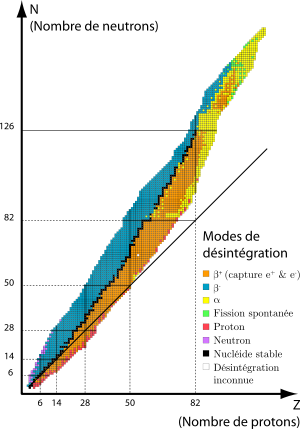
L'explication de ce phénomène est qu'avec l'augmentation du nombre de protons, il y a augmentation relative des forces électromagnétiques répulsives entre ces nucléons identiques, et cela alors que la force nucléaire est moins forte entre nucléons identiques qu'entre nucléons différents. Par conséquent la cohésion de l'atome ne peut être alors préservée que par une augmentation plus importante du nombre de neutrons (d'où l'expression de "colle" pour décrire la fonction de cohésion exercée par les neutrons dans la force nucléaire).
Dans le graphique supra on voit que l'élément stable le plus lourd est le Plomb (126 neutrons pour 82 protons). La droite noire allant de ce point à l'origine des axes est appelée "vallée de la stabilité", car les isotopes instables situés aux alentours ont tendance à se désintégrer (notion de radio-activité) pour dériver vers l'état stable
N.d.A. Il y a là une analogie avec la notion de "puits de potentiel" (que nous étudierons dans le chapitre suivant consacré autres interactions entre les corps).
Radioactivité
Ce phénomène physique par lequel des noyaux atomiques instables se transforment spontanément en d'autres atomes (en émettant simultanément des particules de matière et de l'énergie) est appelé "radioactivité". Dans le graphique ci-dessus les couleurs aux alentours de la ligne de stabilité correspondent à des modes de désintégration c-à-d de radioactivité.
Prenons le cas de la radioactivité du 14C : un des 8 neutrons se transforme en 1 proton, 1 électron et 1 antineutrino. L'augmentation du nombre de protons, de 6 à 7, transforme l'atome de carbone en atome d'azote (transmutation, cf. supra #tableau-periodique). D'autre part l'émission d'un électron correspond à une émission d'énergie que l'on appelle rayonnement/désintégration/radiocativité β–. Nous verrons plus loin qu'il existe différents type de radioactivité, selon le type de particule émise : β+, β–, α.
Radiothérapie. Le phénomène de radioactivité, donc de désintégration de noyaux d'atomes, est utilisé pour détruire des cellules cancéreuses en leur faisant subir un rayonnement radioactif. Celui-ci a pour effet de provoquer une mutation de leur ADN, de sorte que leur reproduction sera bloquée. Un avantage de la radiothérapie est qu'elle ne nécessite pas d'opérer le patient. La radiothérapie doit cependant veiller à ce que ses effets collatéraux c-à-d la destruction de cellules saines ne l'emporte sur la destruction de cellules cancéreuses.
Période
radioactive
La désintégration d'un isotope n'est évidemment pas instantanée, elle dure une certaine période, très variable selon le type d'isotope. D'autre part la vitesse de désintégration est proportionnelle à la quantité d'isotope subsistant (en grammes ou moles), c-à-d qu'à chaque intervalle de temps Δt la quantité N0 diminue du même facteur. Ainsi si le facteur vaut 2 ⇒ on obtient la série de points de coordonnées cartésiennes suivante :
( 0 , N0 )
( 1 , N0 / 2 )
( 2, N0 / 4 )
( 3 , N0 / 8 ), etc.
Ainsi le graphe de la quantité d'un isotope en fonction du temps est une exponentielle.
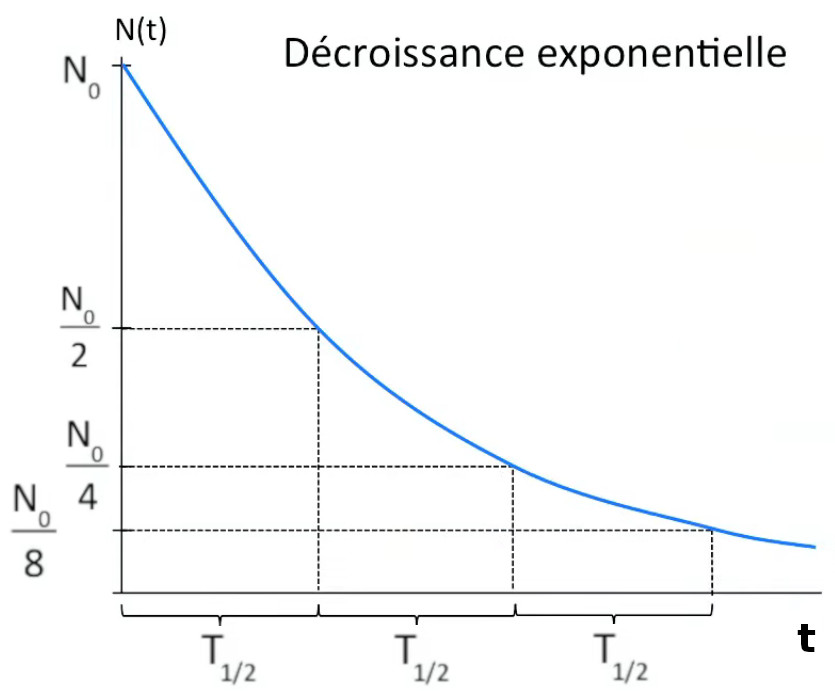
La période T1/2 est la durée au terme de laquelle la quantité a diminué de moitié. Elle est appelée "période radioactive" ou plus simplement "période" d'un isotope. On utilise parfois aussi la dénomination "temps de demi-vie" ou plus simplement "demi-vie" (NB : qui ne signifie pas que l'isotope s'est totalement désintégré au terme de la seconde demi-vie, puisque la courbe est asymptotique à l'axe du temps). La demi-vie constitue donc une mesure temporelle de la radioactivité : plus un nucléide est radioactif ⇒ plus vite il se désintègre ⇒ plus courte est sa période. Il y a donc relation inverse entre période et radioactivité c-à-d entre durée et intensité de la radioactivité.
Le tableau ci-contre montre que la période varie considérablement entre isotope, l'écart couvrant plusieurs ordres de grandeur. On constate notamment la période tellement courte du béryllium-8 (8Be), expliquant pourquoi il n'est pas repris dans le graphe supra #neutron=F(#protons).

C'est typiquement le cas d'un isotope "non naturel" c-à-d qu'on ne peut observer (brièvement) qu'au moyen d'un #accelerateur-particule. Le molybdène-99 (99Mo), qui a une période de 66 heures, sert de précurseur d'éléments utilisés en radiothérapie. La période du célèbre carbone-14 (14Ca) – utilisé pour la datation archéologique – est d'environ 5.730 années. Le carbone-14 est donc plus radioactif que le plutonium-239 (239Pu), utilisé dans les bombes atomiques, et dont la demi-vie est de 24.000 ans. Enfin l'uranium-235 (235U), combustible primaire de la plupart des centrales nucléaires, est encore moins radioactif puisque sa demi-vie est d'environ 700 millions d'années.
C'est à partir d'une période d'un milliard d'années que l'on considère un isotope comme "faiblement radioactif". On considère qu'un élément est stable si sa période est d'au moins mille milliards d'années.
N.d.A. Le scientifique de Clipedia reconnaît que les critères permettant de qualifier un élément de "faiblement" ou "fortement" radioactif ne sont "pas clairs". Il n'en dit malheureusement pas plus. Je suppose que les critères sont d'ordre médical. Il serait intéressant d'en savoir plus, alors que les conditions d'affections sévères causées par la radioactivité semblent semblent être plus difficilement réunies que ce que l'on croyait, comme le suggèrent l'état de la faune et de la flore dans la région de Tchernobyl [source] ou encore la très faible augmentation du nombre de cancers suite à l'accident de Fukushima [source]. Pour une analyse économique de cette problématique voir konfedera.org/developpement-durable#problematique-energetique.
Étudier la technique de datation au carbone-14 est l'occasion d'illustrer des phénomènes physiques et biologiques très importants. À commencer par la photosynthèse, processus par lequel les végétaux captent le CO2 de l'atmosphère et la lumière ambiante comme sources de matière première et d'énergie, pour fabriquer leur matière organique et permettre ainsi leur croissance. Ce CO2 se retrouve donc dans les végétaux et les animaux qui se nourrissent de végétaux, ainsi que les animaux prédateurs d'herbivores. D'autre part une partie constante du carbone dans l'atmosphère est composée de carbone-14 : 14CO2 / CO2 ≈ 10-12. Cette constance est due au fait que la désintégration naturel du 14CO2 en azote est compensée par le fait que dans la haute atmosphère se produit une réaction nucléaire entre rayons cosmiques et azote, qui transforme celui-ci en 14CO2. Le taux de 10-12 se retrouve donc dans les végétaux et animaux, et s'y maintient jusqu'à leur mort (puisque la quantité de 14CO2 est renouvelée par le métabolisme des organismes vivants, et que leur espérance de vie est très inférieure à la période du carbone-14). AU décès des organismes vivants leur métabolisme s'arrête, de sorte que seule opère la désintégration du 14CO2. Par conséquent le taux de 14CO2 contenu dans un débris d'organisme mort permet de déduire la date de celle-ci à partir du graphique supra où N0=10-12. La datation au carbone-14 est suffisamment précise pour des organismes décédés il y a moins de cinquante mille ans. Mais au-delà la quantité de 14CO2 est trop faible que pour être mesurée avec suffisamment de précision (⇒ on utilise aujourd'hui d'autres isotopes pour la datation archéologique).