II. Mesure
Unités de mesures
Les notions de mesure, dimension et unités sont indispensables pour résoudre des problèmes scientifiques concrets.
Mesure
et unité
Mesurer une longueur/distance, c'est compter le nombre d'unités de mesure qu'elle contient. Ainsi lorsqu'une mesure donne le résultat formulé par L = 4 cm, cette notation est une façon simplifiée d'exprimer que L = 4 * 1 * cm où 1 * cm = 1 cm est l'unité de mesure de la grandeur mesurée (qui est en l'occurrence une longueur).
Dimension
Il y a différentes natures (types) de grandeurs physiques. Cependant le terme mathématique n'est pas "nature" ou "type" mais dimension. Il existe sept dimensions fondamentales [source] :
| Dimension | Unité |
|---|---|
| Longueur (L) | mètre : m |
| Masse (M) | kilogramme : kg |
| Temps (T) | seconde : s |
| Courant électrique | ampère : A |
| Température thermodynamique | kelvin : K |
| Quantité de matière | mole : mol |
| Intensité lumineuse | candela : cd |
N.B. Plusieurs unités de mesure peuvent correspondre à une même dimension. Par exemple :
- longueur : cm, m, km, ...
- masse : g, kg, ...
- temps : s, m, h, ...
Dimension
et unité
dérivées
Pour illustrer la notion de dimension et unité dérivées, prenons le cas du calcul de la surface d'un rectangle :
S = L * l
par exemple :
S = 5 cm * 4 cm ⇔
S = 5 * cm * 4 * cm ⇔
S = 5 * 4 * cm * cm ⇔
S = 20 cm2
Algébriquement, les unités de mesure doivent donc être traitées comme de simples nombres. Apparaît alors ici que l'unité de surface est le carré de l'unité de longueur considérée.
On peut généraliser de cet exemple que :
- la surface est une dimension dérivée de la dimension de base longueur ;
- le cm2 est une unité de surface dérivée du cm.
Appliquons maintenant ces connaissances à un cas un peu plus complexe : le calcul d'une vitesse :
v = l / t
par exemple :
v = 14 mm / 7 s ⇔
v = 14 * mm / ( 7 * s ) ⇔ (cf. supra /preambule#fractions) :
v = 14 * mm / 7 / s ⇔
v = 14 / 7 * mm / s ⇔
v = 2 mm/s
On peut donc généraliser de cet exemple que :
- la vitesse est une dimension dérivée des dimensions de base longueur et temps ;
- le mm/s est une unité de vitesse dérivée du mm et de la s.
Un dernier petit exercice pour nous familiariser avec ces notions :
Soit :
• v = 20 m/s
• t = 30 s
étant donné que :
l = v * t ⇒
l = 20 m/s * 30 s ⇔
l = 20 * m / s * 30 * s ⇔
l = 20 * 30 * m / s * s ⇔ (cf. supra /preambule#fractions) :
l = 600 * m * s / s ⇔
l = 600 m
Unite de surface (N.d.A.)
Reprenons les notions développées supra, sur base d'un cas simple : la surface d'un carré de 10 mètres de côté vaut :
10 m * 10 m =
10 * m * 10 * m =
10 * 10 * m * m =
102 * m2 =
100 * m2 =
100 m2
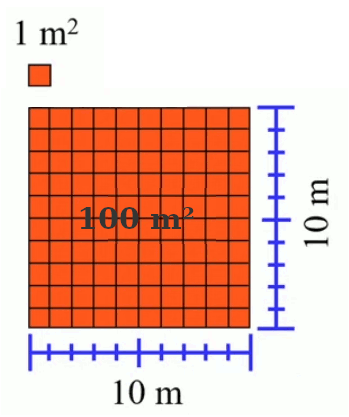
100 m2 c'est bien cent fois (ici 10*10) l'unité de surface (1 m2).
Généralisation :
x m2 =
x1/2 * x1/2 m2=
x1/2 m * x1/2 m
Le cas particulier de l'unité de surface 1 m2 c-à-d pour x=1 :
1 m2 =
11/2 m * 11/2 m =
1 m * 1 m
Ainsi la caractéristique de l'unité de surface (1 m2) est qu'elle a la même valeur numérique que les longueurs qui la composent (1 m), lesquelles sont toutes deux égales à l'unité de longueur (1m). Cette particularité – qui fait d'elle l'unité de surface – la distingue de toute autre mesure de surface : par exemple, la surface 100 m2 n'a pas la même valeur numérique que les deux longueurs qui la composent (10 m * 10 m, ou encore 100 m * 1 m), et ces longueurs ne sont pas toutes deux égales à l'unité de longueur.
Les notations d'unité doivent être traitées algébriquement comme les nombres.
Surfaces
Ainsi pour l'unité de surface (x*y) en mètres (m) :
S = x m * y m = x * y m m = x * y m2
N.B. On ne place pas le signe de multiplication avant l'indicateur d'unité, ce signe est donc implicite.
Supposons maintenant qu'on veuille calculer le nombre N de briques de surface latérale de 75 cm2 nécessaire pour construire un mur de 3 m2 :
N = 3 m2 / ( 75 cm2 ) =
3 m m / ( 75 cm2 ) =
3 * 100 cm * 100 cm / ( 75 cm2 ) =
3 * 10.000 cm cm / ( 75 cm2 ) =
3 * 10.000 cm2 / ( 75 cm2 ) =
NB : les unités de mesure au numérateur et dénominateur s'annulent comme des nombres :
30.000 / 75 = 400
NB : ce nombre de brique est dit "sans dimension" : aucune unité de mesure ne lui est associée.
N.d.A. Autre exemple : 1 µm2 = 1 µ2 m2 = (10-6)2 m2 = 10-12 m2
Vitesse
Passons maintenant aux unités composées. Quelle est la vitesse moyenne en km/h atteinte par le recordman du monde du 100 mètres (9s58, Usain Bolt, 2009) ?
v = 100 m / 9,58 s
or 1 km = 1000 m ⇔ 1 m = 1 / 1000 km
et 1 h = 60 m = 60 * 60 s = 3600 s ⇔ 1 s = 1 / 3600 h
⇒
v = 100 * 1 / 1000 km / ( 9,58 * 1 / 3600 h ) ⇔
v = 100 / 1000 / 9,58 * 3600 km/h = 37,6 km/h
N.B. Il s'agit là de la vitesse moyenne. Or la vitesse de départ est de zéro ⇒ il y a une accélération conduisant à une vitesse maximale vers la fin de course. Cette vitesse de pointe atteinte par Bolt fut d'environ 45 km/h (PS : l'antilope et le guépard peuvent atteindre une vitesse de pointe d'environ 95 km/h : source).
Température
Le passage des mesures de température entre degrés Celsius et Fahrenheit se fait selon l'équation T C = ( T F - 32 ) / 1,8.
Angles
Nous allons montrer ici la différence entre la mesure d'un angle en radians ou en degrés, et l'avantage de la mesure en radians.
Angle en radian. On définit un angle de 1 radian comme celui qui intercepte, dans un cercle de rayon R, un arc de cercle de longueur égale à R. Formellement, pour un angle α en radians, on a α = L / R où L est la longueur de l'arc. Ainsi, si L=R, alors α=1 radian.
Autrement formulé, α = a radians ⇔ arc(α) = a * R
.
où arc(α) – qui correspond à L dans la formulation supra – est donc exprimé en unités de longueur de R.
En particulier α = 1 radian ⇔ arc(α) = R : exprimer l'angle α en radians (rad) c'est donc l'exprimer par rapport à une unité correspondant à une longueur d'arc égale au rayon R.
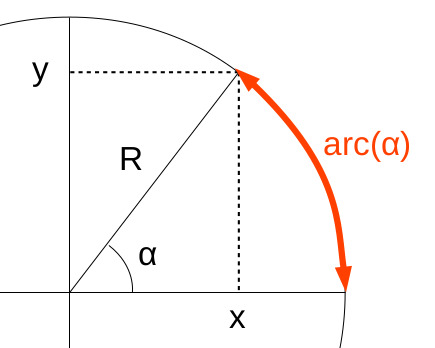
N.d.A. Le radian n'est pas la longueur de l'arc (qui est L), mais une mesure d'angle. On définit 1 radian comme l'angle central qui intercepte un arc de cercle dont la longueur est égale au rayon. Autrement dit, il s'agit d'un rapport (L/ R) qui est sans dimension, et non d'une mesure de longueur.
Angle en degré. Le degré est défini par rapport au radian et au nombre π ("Pi"). Soit C la circonférence d'un cercle de rayon R :
π = C / R / 2
⇔
C = 2 * π * R
or par définition :
360 deg = C / R rad ⇒
360 deg = 2 * π rad ⇔
1 deg = π / 180 rad
⇔
1 rad = 180 / π deg ≈ ⇔
1 rad ≈ 180 / 3,1416 deg = 57,3 °
Le tableau suivant résume les développements ci-dessus sous forme de règles de trois.
| RAD | ARC | DEG |
|---|---|---|
| θ | θ * R | ? |
| 2 * π | 2 * π * R | 360 |
| 1 | R | 360 / ( 2 * π ) |
| 1 | R=1 | 180 / π ≈ 180 / 3,1416 = 57,3 |
Un intérêt du radian, en liant toute grandeur d'angle à une longueur d'arc correspondante (pour un R déterminé *), est de faciliter la mesure des angles : on mesure la longueur de l'arc ⇒ on en déduit la taille de l'angle en degrés (alors que pour mesurer directement en degré il faut utiliser un rapporteur).
(*) Mais dans le cercle trigonométrique on suppose toujours R=1
Puissance et exposant
L'expression a2 se lit "a exposant 2" ou encore "a puissance 2". Mais elle se lit aussi "a carré" car a2 est la surface d'un carré de côté de longueur a. De même a3 se lit "a exposant 3" ou encore "a puissance 3". Mais elle se lit aussi "a cube" car a3 est la surface d'un cube d'arrête a.
La notion de puissance est illustrée dans nombre d'applications du monde physique :
- au 19° siècle Ludwig Boltzmann a démontré que tout corps chauffé émet de la lumière dont l'intensité est proportionnelle à la puissance quatre de sa température : I = c * T 4 exprimant ainsi une forte sensibilité de l'intensité lumineuse par rapport à la température du corps : quand on double la température l'intensité est multipliée par 24=16.
- au 17° siècle Isaac Newton a montré que la lune est attirée par la Terre par une force (dite "gravitationnelle") proportionnelle à l'inverse du carré de la distance séparant les deux astres : F = C / d 2 : si cette distance doublait cette force diminuerait d'un facteur 1/22=1/4.
- la notation exponentielle (ou "scientifique") permet également d'exprimer simplement des grandeurs très élevées, telles que la vitesse de la lumière :
c = 300.000.000 m/s ⇔
c = 3 * 100.000.000 m/s ⇔
c = 3 * 108 m/s
 Vidéos Clipedia : Puissance et exposant : règles de calcul // Puissances négatives : règles de calcul
Vidéos Clipedia : Puissance et exposant : règles de calcul // Puissances négatives : règles de calcul
Par définition de l'exposant :
a pi = π pi a
Règles de calcul :
- produit de puissances :
π n ( a pi ) = a ∑ n pi
Exemple : ( a u * a v ) = a u+v
Démonstration :
π n ( a pi ) =
π n ( π pi a ) =
π p1 a * ... * π pn a =
a ∑ n pi
CQFD
P.S. On peut alors démontrer que a 0 = 1 (sauf si a=0, dans lequel cas il y a indétermination) :
a m * a 0 = a (m+0) ⇔
a m * a 0 = a m ⇔
a 0 = 1
CQFD - puissance de produit :
( π a ) n = π ( a n )
Exemple : ( x * y ) n = x n * y n
Démonstration :
( π a ) n =
par définition de l'exposant
π n ( π a ) =
par commutativité du produit
π ( π n a ) =
π ( a n )
CQFD - puissance de puissance :
( a m ) n = a m * n
Démonstration :
( a m ) n =
π n ( a m ) =
par (5) :
a ∑ n m =
a m * n
CQFD - quotient de puissance :
a m / a n = a m - n
Démonstration :
a m / a n =
π m ( a ) / π n ( a ) =
π m-n ( a ) =
a m - n
CQFD
Ce qui permet d'introduire la notion d'exposant négatif en posant m=0 dans (9) :
a 0 / a n = a 0 - n ⇒
par (6) :
1 / a n = a - n qui est donc la définition de a - n.
Logarithme
Définition
Soit la fonction exponentielle y (x) = b x ou b est appelé "base de la fonction exponentielle", on appelle alors "fonction logarithmique en base b" la fonction logb (y) = x. La définition du logarithme est donc (en simplifiant y (x) par y) :
y = b x ⇔ logb (y) = x
- L'opération de gauche à droite est appelée "passage au logarithme".
- Par convention lorsque b=10 on ne mentionne pas la base : log x = log10 x
Autrement dit (en lisant l'équivalence de droite à gauche) : le logarithme en base b (logb) d'un nombre y est la puissance en base b qui donne ce nombre y.
Fonctions réciproques. Les fonctions logarithme log(x) et exponentielle exp(x) sont réciproques, c-à-d que log( exp(x) )= exp( log(x) ) = x :
- exp( log(x) ) = x : en substituant la valeur de x du membre de droite de l'équivalence (10) dans le membre de gauche ⇒ y = b logb (y) ;
- log( exp(x) ) = x : en substituant la valeur de y du membre de gauche de l'équivalence (10) dans le membre de droite ⇒ logb ( b x ) = x.
Applications
Nous allons maintenant montrer l'utilité du logarithme pour (i) rendre possible la comparaison de mesures d'ordres de grandeurs très différentes ; (ii) faciliter le calcul du produit de grand nombres ; (iii) mesurer la perception auditive.
Ordre de grandeurs. Dans l'échelle de mesure suivante, dont l'unité est le mètre, on peut comparer un humain et un cétacé, mais on ne peut distinguer les corps d'ordres de grandeur inférieurs au mètre, ni mesurer ceux d'un ordre de grandeur dépassant la largeur de l'écran (ici un séquoia).
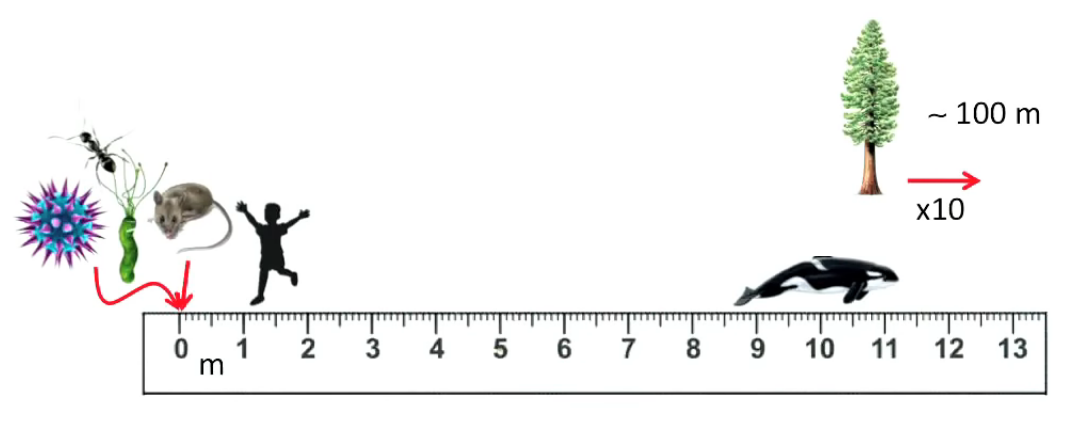
Pour résoudre ce problème il suffit de passer à la notation scientifique (ou notation exponentielle) des ordres de grandeur :
| virus | ~ 0,1 µm | 10- 7 m |
| bactérie | ~10 µm | 10- 5 m |
| fourmi | ~ 1 mm | 10-3 m |
| souris | ~ 1 cm | 10-2 m |
| humain | ~ 1 m | 100 m |
| cétacé | ~ 10 m | 101 m |
| séquia | ~ 100 m | 102 m |
Il suffit alors de passer au exposant pour obtenir l'échelle dite "logarithmique", qui est telle que 10 - (n-1) / 10 - n = 10 (rapport constant), alors que l'échelle précédente correspond à un rapport n / n - 1 (le rapport tend vers 1 lorsque n augmente).
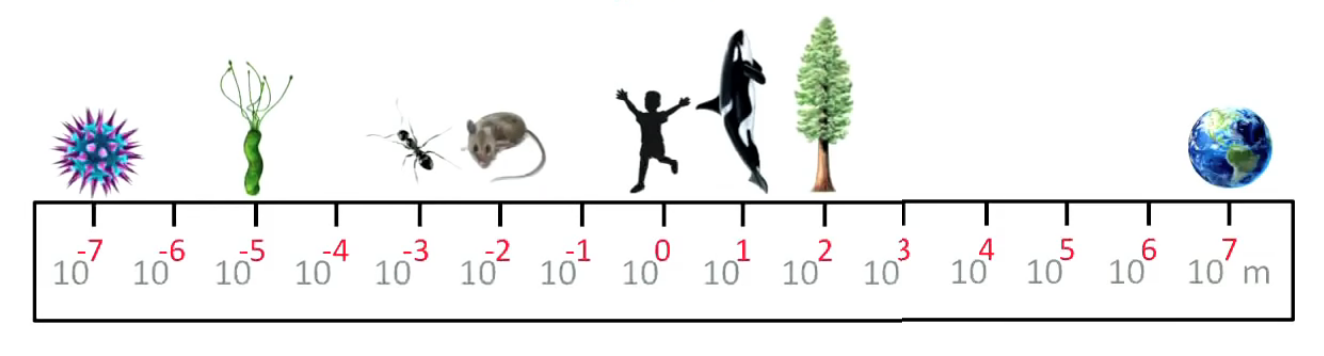
Cette échelle fait bien appel à la notion de log. Ainsi prenons le cas de la fourmi : log(1mm)=log(0,001m)=-3 car 0,01=10-3.
Simplification de calculs. La notion de logarithme a été développée au 17° siècle par John Napier pour faciliter les calculs impliquant des grands nombres (exemple : 3.5478.341 * 6.148.632). Cette technique de simplification exploite la propriété π n ( a ei ) = a ∑ n ei (5) :
Soit 3.5478.341 = A et 6.148.632 = B ⇒ par (5) :
log ( A * B ) = log (A) + log (B) ⇒
pour calculer A * B il suffit de :
1. chercher log(A) et log (B) dans la table des logarithmes
2. calculer log (A) + log (B) ⇒ on connaît log ( A * B ) ⇒
3. chercher log ( A * B ) dans la table de logarithmes
4. on trouve A * B à la même ligne de la colonne adjacente.
CQFT
Perception auditive. L'échelle logarithmique correspond à divers phénomènes naturels tels que l'audition. L'oreille humaine moyenne peut percevoir des intensités sonores comprises entre 10-12 W/m2 (noté I0 et appelé "seuil d'audibilité) et 1 W/m2 (appelé "seuil de dommage" : au-delà l'intensité commence à provoquer des lésions).
Mais l'intensité perçue par l'oreille humaine ne répond pas à la même dynamique que l'intensité mesurée par un appareil de mesure (microphone + sonomètre). Ainsi le graphique suivant montre que si la puissance de la source sonore est doublée la perception de cette variation par l'oreille est inférieure à ce facteur 2, et en outre cet effet d'amortissement (ou plutôt de saturation) augmente avec le niveau de puissance de la source. Le graphique suivant exprime cela de façon inverse : pour doubler la perception d'un son par l'oreille humaine il faut multiplier la source par un facteur croissant. Il apparaît que cette croissance est exponentielle : pour augmenter la perception de n à 2n la source doit augmenter de 10n (exemple : pour que la perception passe de 4 à 8 la source doit augmenter de 104.
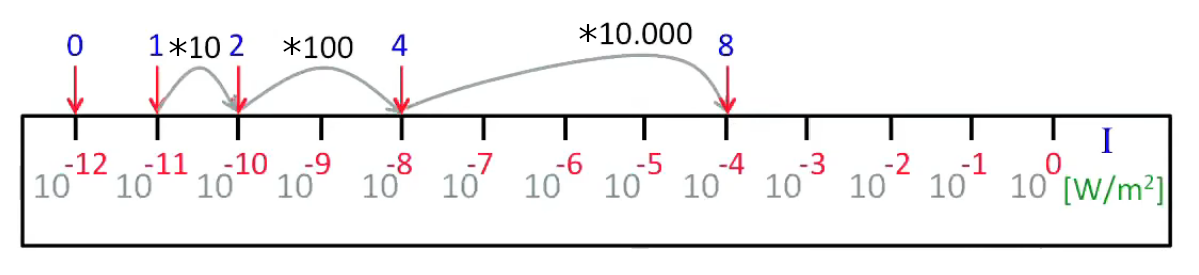
Le zéro est placé à I0 et l'unité est fixée arbitrairement à 10 * I0.
On peut alors concevoir une unité sonore spécifique à l'oreille humaine pour obtenir une échelle mesurant l'intensité perçue par l'oreille humaine. Pour ce faire on opère en deux phases :
- Dans la seconde règle du graphique ci-dessous on exprime l'intensité sonore I en x unités du seuil d'audibilité I0 : I = x * I0 = x * 10-12 W/m2 :
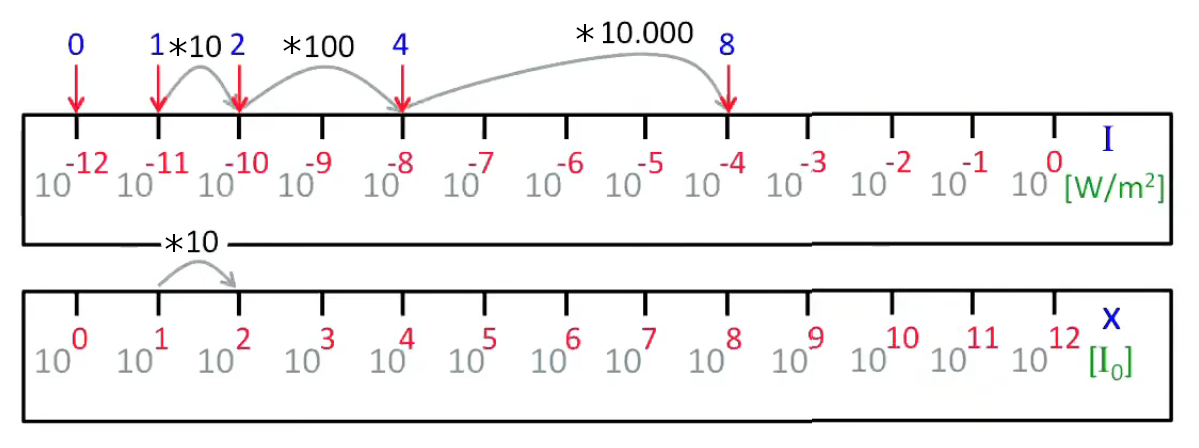
Notez les unités différentes (à droite en vert).
Dans ces conditions y = log x traduit le fait que l'intensité sonore perçue (y) répond de façon logarithmique à l'intensité sonore mesurée (x). L'unité de y est appelée "bel" (en hommage à Graham Bell), mais en pratique on utilise plutôt le dB : y = 10 log x [dB].
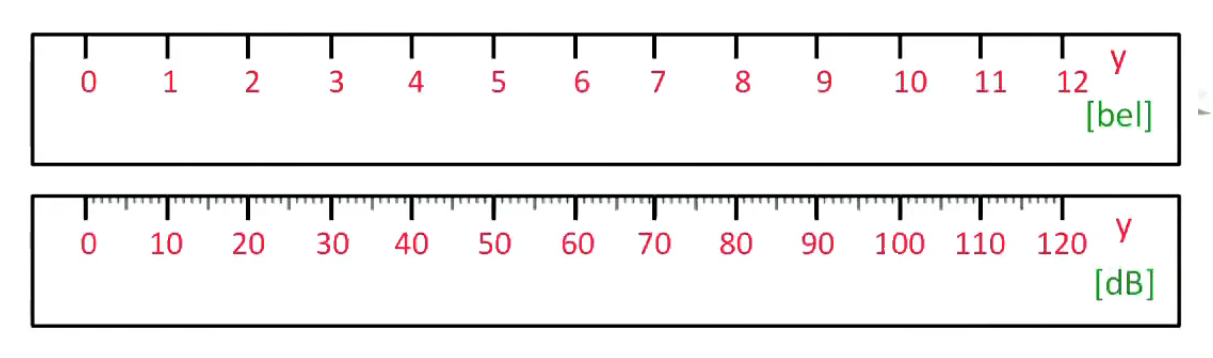
Comparons les intensités sonore de la voiture (V) et de la moto (M) :
40 = 10 (log xV)
80 = 10 (log xM)
⇔
xV = 10 4
xM = 10 8
⇒ par (9) :
xM / xV = 10 4
Interprétation : alors que la puissance sonore mesurée du moteur de moto est 10.000 fois supérieur à celle de la voiture nous ne percevons qu'une différence par un facteur 80/40=2 (PS : quant à la différence, perçue ou mesurée, entre voiture et moto, c'est grâce à la longueur plus grande de son pot d'échappement que la voiture amortit mieux la pression acoustique émise par les pistons du moteur à explosion).
Propriétés
Si dans l'équivalence y = b x ⇔ logb (y) = x (10) on substitue la valeur de y du membre de gauche de dans le membre de droite, on obtient que :
logb b x = x
c-à-d que le logarithme de l'exponentielle, c'est la fonction identité.
Et si dans cette même équivalence y = b x ⇔ logb (y) = x (10) on applique la fonction exponentielle à l'égalité de droite, alors on en déduit, par comparaison avec l'égalité de gauche, que :
b logb y = y
c-à-d que l'exponentielle du logarithme, c'est aussi la fonction identité.
Logarithme et exponentielle sont donc des fonctions réciproques.
On obtient le graphe de la fonction log à partir de la fonction exp par deux rotations : 90° à sens horaire, puis 180° de bas en haut.
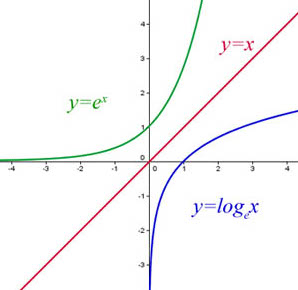
Les nombres négatifs ne font pas partie du domaine de la fonction log (exemple : -3 = 10 ?).
| logb 0 = - ∞ | car | 0 = b - ∞ |
| logb 1 = 0 | car | 1 = b 0 |
| logb ∞ = ∞ | car | ∞ = b ∞ |
Règles de calcul :
- logarithme d'un produit :
En remplaçant pi par logb(pi) dans π n b pi = b ∑ n pi (5) ⇒
π n b logb pi = b ∑ n logb pi ⇒ par (13) :
π n pi = b ∑ n logb pi ⇔
log π n pi = log ( b ∑ n logb pi ) ⇔ par (11) :
logb π n pi = ∑ n logb pi - logarithme d'une puissance :
en remplaçant m par logba dans ( b m ) n = b m * n (8) ⇒
( b logb a ) n = b n * logb a ⇔
a n = b n * logb a ⇔
logb a n = n * logb a - logarithme d'un quotient :
en remplaçant m par logbm et n par logbn dans a m / a n = a m - n (9) ⇒
a logb m / a logb n = a logb m - logb n ⇔
m / n = a logb m - logb n ⇔
log ( m / n ) = logb m - logb n -
Soit
x = a loga x ⇒
b = a loga b
substitué dans :
x = b logb x ⇒
x = ( a loga b ) logb x ⇔
x = a loga b * logb x ⇒
égalité entre les membres de droite des 1° et 5° égalités ⇒
loga x = loga b * logb x
En particulier si x=a ⇒
loga a = loga b * logb a
1 = loga b * logb a ⇔
loga b = 1 / logb a
Enfin on notera que dans la pratique ce sont essentiellement trois bases qui sont utilisées : 10, 2 (notamment en informatique) et e=2,718281... (où loge est noté ln et appelé logarithme népérien en honneur à John Napier).
Numération de position
La vidéo reproduit de manière fictive la mise au point d'une technique de comptabilité ("compter et enregistrer le résultat par une écriture") d'un cheptel de moutons, cela à une époque (4° millénaire av. J.C.) où l'écriture, qui venait à peine d'être inventée, se faisait sur des tablettes d'argile. Ce type d'enregistrement peut également servir dans le cas de contrats de vente.

Marquer sur la tablette un trait par mouton constitue un système de comptabilité assez primaire. N'étant fondé sur un vocabulaire composé que d'un seul symbole, il n'est pratique que pour un nombre limité de moutons/traits, au delà duquel la quantité écrite ne peut plus être lue par le cerveau humain mais doit être comptée (N.d.A : la limite se situant disons autour de six). Le seul véritable progrès à ce stade est que le comptage des moutons ne doit plus être fait en présence du cheptel, grâce cet l'enregistrement (pour autant que celui-ci soit à jour et sans erreur).

La "main arbre" est un figure fractale.
Pour améliorer ce système on va utiliser un outil de comptage portatif, en l'occurrence la main, dont les cinq doigts vont constituer un référentiel. Cette main, ou plutôt le nombre de doigts qui la constituent, vont être représentés par le signe |||| : une forme ancienne de notre chiffre 5 vient d'être ainsi inventée !
N.d.A. : |||| devient la représentation écrite de la quantité que représentent les doigts de la main, et peut donc être qualifiée de "chiffrement par regroupement".
Cette technique de comptabilité est clairement plus efficace : si par exemple l'information de quantité que le cerveau pouvait enregistrer en une fois (c-à-d lire sans compter) était de six avec la technique du trait unique, cette limite est désormais repoussée à 5*6=30 (quantité correspondant au nombre de doigts de six mains).

Cependant le nombre de paquets de cinq ne correspond pas nécessairement au nombre de moutons ⇔ il faut pouvoir également comptabiliser d'éventuelles unités restantes en nombre inférieur à celui d'un paquet.
Pour ce faire, on va marquer sur la plaque d'argile un long trait pour séparer l'écriture des paquets (à gauche) et des unités (à droite), de sorte qu'à gauche un paquet va pouvoir être représenté non plus par |||| mais par une "unité de cinq", et donc par un trait unique (cf. la "main arbre" supra). NB : cette innovation introduit donc la notion de position dans l'écriture de quantités, c-à-d dans la numération ⇒ le titre de la vidéo : "Numération de position".

Ainsi l'on repousse à nouveau la limite de lecture-vs-calcul, cette fois de 5*6=30 à 5*30=150 ! En effet, à gauche un paquet n'est pas un paquet d'unités mais un paquet de paquets : à gauche, |||| est l'équivalent de |||| |||| |||| |||| |||| à droite.

En outre ce principe de position peut être reproduit à une troisième colonne (cf. principe fractale de la "main arbre" supra).
Dans notre système de comptabilisation, désormais composé de trois positions et deux caractères (| et ||||), les unités de la colonne de gauche représentent 25 unités de la première colonne, tandis que la colonne centrale représente 5 unités de la première colonne. Par conséquent 27 moutons ne doivent plus être représentés par 27 traits, mais par seulement trois : un dans la troisième colonne et deux dans la première.

Visualisation intuitive : un trait de la colonne de gauche représente le nombre de doigts de la "main arbre" supra
NB : le nombre de traits dans une colonne sera toujours ≤4, car dès que l'on dépasse quatre on passe à la colonne suivante (vers la gauche). Et c'est évidemment dans cette limitation à quatre traits que réside la facilité de lecture. Ainsi la tablette ci-contre (fictive) acte un contrat passé entre Xavier et Thorgan, qui ont convenu d'échanger neuf moutons contre cinquante trois poulets.

Ce système de numération peut cependant être encore amélioré. On voudrait notamment trouver un moyen de supprimer les traits de séparation. Pour ce faire, sans semer la confusion, il suffit de deux opérations :
- remplacer les traits d'unité verticaux par des traits obliques enchaînés, de sorte de /\ représente deux unités, \/\ représente trois unités, et \/\/ représente quatre unités ;
- remplacer la représentation d'un colonne vide || par le signe 0.
Ainsi ll||lll s'écrira désormais /\0\/\ pour représenter notre 53 (NB : dans les trois cas on a bien 50+0+3).
Notre système de numération est désormais composé de cinq symboles : 0, |, /\, \/\, \/\/. NB : malgré que la main fut notre référence initiale, il n'est pas étrange qu'il n'existe pas de symbole de base pour le nombre cinq, car lorsque l'on dépasse quatre, c-à-d dès que l'on atteint cinq, on change de position : ainsi "cinq" s'écrit l0. Ce nombre qui détermine le passage à une position (colonne) supérieure, et qui est également le nombre de symbole du système, s'appelle la base du système de numération (nous sommes donc ici dans un système de base 5).
On peut en effet concevoir une infinité de systèmes de numération de position, chacun déterminé par sa base ! Ainsi nous allons voir que :
• la représentation du nombre cinq en base 10 (soit 5) s'écrit (l0) en base 5 ;
• le nombre dix en base 5 s'écrit /\0.
N.d.A. Par convention, la base utilisée pour mentionner l'ordre d'une base est la base d'ordre 10.
Notre système de numérotation (0,1,2,3,4,5,6,7,8,9) étant composé de dix symboles, nombre qui constitue le passage à une position supérieure, est donc de base 10. Ce système serait né en Inde, dont les perspicaces savants avaient remarqué que nous avions deux mains. Ainsi dans le système de notation avec les seuls traits verticaux, mais en base 10, le nombre vingt-quatre s'écrit ll|llll ⇒ dans notre écriture fictive /\ \/\/ ⇒ dans notre écriture arabe 24.
La dernière ligne du tableau suivant montre que lorsqu'on travaille avec diverses bases, on éviterait de possibles confusions si l'on utilisait des symboles spécifiques pour chaque base. Mais il faudrait pour cela connaître autant de séries de symboles qu'il y de bases différentes ...
| Base 5 | Base 10 | |
|---|---|---|
| | l | ll | lll | l | lll |
| 0 l /\ \/\ \/\/ | /\ \/\ | l \/\ |
| 0 1 2 3 4 5 6 7 8 9 | 23 | 13 |
La dernière base apparue est la base 2, qui est particulièrement adaptée au mode de fonctionnement des appareils électroniques (dont les ordinateurs), où l'absence de courant est associé au symbole 0, et la présence d'un courant au symbole I.
| Base 2 | Base 5 | Base 10 | |
|---|---|---|---|
| | l | l | l | | l | l | l | | ll | ll | lllllll |
| 0 1 | 11011 | ||
| 0 1 2 3 4 | 102 | ||
| 0 1 2 3 4 5 6 7 8 9 | 27 |
N.d.A. Systèmes de numérotation : formalisation
Commente convertir un nombre exprimé en une base quelconque vers une autre base.
Exemple : pour convertir 6,3 (base 10) vers la base 2, on procède en trois étapes :
conversion de la partie entière (6), en divisant successivement par la base (2) et en notant les restes par rapport à la partie entière du quotient (c-à-d qu'on ignore les décimales) :
• 6 / 2 = 3,... ⇒ reste 6 - 3 * 2 = 0 ⇒ on recommence avec la partie entière du quotient :
• 3 / 2 = 1,... ⇒ reste 3 - 1 * 2 = 1 ⇒ on recommence avec la partie entière du quotient :
• 1 / 2 = 0,... ⇒ reste 1 - 0 * 2 = 1 ⇒ stop car la partie entière du quotient est zéro.
⇒ en lisant les restes de bas en haut, on obtient : 610=1102
Et pour faire la conversion inverse il suffit de calculer :
0 * 20 + 1 * 21 + 1 * 22 = 6N.B. : (40)10 = 0 * 100 + 4 * 101
conversion de la partie fractionnaire (0,3), en multipliant successivement par la base (2), et on prend la partie entière de chaque résultat, jusqu'à obtenir un résultat fractionnaire nul (ou approchant, car parfois on tombe dans un cycle infini) :
• 0,3 * 2 = 0,6 ⇒ on retient la partie entière (0) comme premier chiffre après la virgule en base 2, puis on continue avec la partie fractionnaire (0,6) :
• 0,6 × 2 = 1,2 ⇒ on retient la partie entière (1) comme second chiffre après la virgule en base 2, puis on continue avec la partie fractionnaire (0,2) :
• 0,2 × 2 = 0,4 ⇒ on retient la partie entière (0) comme troisième chiffre après la virgule en base 2, puis on continue avec la partie fractionnaire (0,4) :
• 0,4 × 2 = 0,8 ⇒ on retient la partie entière (0) comme quatrième chiffre après la virgule en base 2, puis on continue avec la partie fractionnaire (0,8) :
• 0,8 × 2 = 1,6 ⇒ on retient la partie entière (1) comme cinquième chiffre après la virgule en base 2, puis on remarque que la fraction revient à 0,6 (deuxième étape ci-dessus), ce qui va recommencer le cycle ⇒ stop ⇒ 0,310 = 0.01–0–0–1–2 où la partie 1–0–0–1–2 est périodique.
Et pour faire la conversion inverse il suffit de calculer :
0 * 2-1 + 1 * 2-2 + 0 * 2-3 + 0 * 2-4 + 1 * 2-5 = 0 + 1/4 + 0 + 0 + 1/32 = 9/32 = 0,28135 ≈ 0,3Meilleures approximations suivantes :
0,28135 + 2-6 = 0,296975
0,296975 + 2-9 = 0,298928125
etc.- Réunir parties entière et fractionnaire ⇒ : 6,310 = 110.01–0–0–1–2
NB : wims.univ-cotedazur.fr donne 110.0100110.0100110011001... où je ne comprends pas la partie surlignée en rouge ...
La comparaison des additions permet d'affiner la compréhension intuitive des systèmes de numérotation. Ainsi le tableau suivante montre que 2+3=5 en décimal correspond à 10+11=101 en binaire, ce que l'on peut vérifier ... en n'oubliant pas que toute addition se calcule en commençant par la droite :
– un plus zéro donne un et je ne retiens rien ;
– un plus un donne deux, je pose zéro et je retiens un ;
– un plus zéro donne un.
ce qui donne 101 [source, p.391, édition 2024].
| Décimal | Binaire |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| ... | ... |
Exercice. Calculez la colonne de droite comme pour celle de gauche :
1=0+1
2=1+1
3=2+1
4=3+1
etc
Notation hexadécimale
Alors que la conversion entre base 2 et base 10 est laborieuse, celle entre la base 2 et une base puissance de 2 est beaucoup plus maniable, en raison du la règle des faisceaux (non démontrée ici) selon laquelle chaque groupe de n chiffres d’un nombre binaire correspond à un chiffre de ce nombre converti en base 2n. La valeur n=4 correspond à la notation hexadécimale c-à-d en base 16. Les chiffres de la notation hexadécimale les chiffres arabes de 0 à 9 et les lettres majuscules de A à F qui notent respectivement les nombres 10 à 15 [source, p.394, édition 2024].
Prenons un exemple avec un nombre binaire de m=12 bits que nous voulons convertir en base 2n = 24 = 16 (soit en hexadécimal). Pour ce faire, nous allons regrouper les bits par blocs de n=4.
Considérons le nombre binaire suivant :
101111010110
On peut regrouper ce nombre en trois blocs de 4 bits :
1011 1101 0110
Ensuite, on convertit chaque bloc en base 16 :
1011 = 1110 = B16
1101 = 1310 = D16
0110 = 610 = 616
Le nombre binaire 101111010110 devient donc BD6 en base 16.
On notera qu’un octet correspond à un nombre compris entre 0 et 255 (111111112 = 25510), représenté en hexadécimal par deux chiffres (FF). Ce mode de représentation est très utilisé par les informaticiens.
https://clipedia-txt.net/mesure#systemes-numerotation