I. Préambule

Culture générale scientifique

Quoi

Cette publication vous permet d'apprendre ou revoir l'essentiel de la matière scientifique supposée connue à la fin des études secondaires (orientation sciences) en mathématique et physique, ainsi que (dans une moindre mesure) chimie et biologie.

Elle intéressera donc particulièrement les personnes se préparant à des études supérieures scientifiques, ou souhaitant simplement se doter d'une culture générale scientifique de base, tout en développant leurs capacités intellectuelles (conseil : pratiquez des séances courtes mais quotidiennes, par exemple le soir, en substitut de la télévision).

Clipedia PDF

Comment

Pour ce faire, clipedia-txt.net présente des synthèses écrites (et illustrées) des exceptionnelles vidéos de clipedia.be. Ces vidéos sont réalisées par une équipe dirigée par Marc Haelterman, professeur à l'École polytechnique de l'Université libre de Bruxelles.

Responsabilité. La publication clipedia-txt.net est mon initiative personnelle. Je suis seul responsable des éventuelles erreurs d'interprétation ou d'incompréhension de ma part. D'autre part, j'ajoute parfois des réflexions ou éléments personnels, que j'identifie par "N.d.A".

Pour réaliser un résumé, je procède à (au moins) trois visionnages de la vidéo :

1. sans prises de notes ;
2. en rédigeant en parallèle le résumé (plus traitement des images) ;
3. lectures parallèles de la vidéo et du résumé, pour y apporter corrections et améliorations.

Exhaustivité

Selon Haelterman, il faudrait environ 500 vidéos pour couvrir l’essentiel du programme de l’enseignement des sciences et des mathématiques du niveau secondaire et du niveau de la première année d’études supérieures scientifiques. Or clipedia.be en est aujourd'hui à environ 230 vidéos réalisées. Pour donner un coup de pouce financier à clipedia.be (ils en ont bien besoin ...), c'est par ici.

Intuition

Les vidéos de clipedia.be privilégient l'approche pratique et intuitive, plutôt que la rigueur mathématique pure : c'est ce qu'on appelle de façon imagée "faire des maths avec les mains".

Syllabus

La publication web en édition continue clipedia-txt.net constitue donc un "syllabus web" (dont la taille est actuellement de 527 pages en équivalent PDF). D'une part la matière est structurée de façon "logico-historique", par un sommaire numéroté, composé de chapitres, sections et sous-sections. En outre, les formules importantes sont numérotées (en rouge) et peuvent être ainsi référencées par lien hypertexte (en bleu) à d'autres endroits (plus souvent supra que infra) de la publication.

En début de chaque section de clipedia-txt.net est mentionnée la vidéo correspondante (lien hypertexte renvoyant vers la video sur clipedia.be).

Complémentarité

Les vidéos de clipedia.be et leurs synthèses écrites (+ images) de clipedia-txt.net sont idéalement complémentaires, les synthèses facilitant notamment la révision et l'approfondissement des vidéos. Le tableau suivant illustre de façon synthétique la complémentarité entre les deux approches, et qui fait de clipedia.be + clipedia-txt.net un système de formation unique au monde (francophone, à ma connaissance) :

	clipedia.be	clipedia-txt.net
Interface	vidéo (⇒ accès séquentiel)	texte + images (⇒ accès direct)
Structuration	classement alphabétique (approche en graphe)	classement numérique (approche historique)

Il me semble que l'approche en graphe de clipedia.be reflète mieux la complexité – interconnectée et rétroactive – du savoir scientifique, de sorte qu'elle sera probablement préférée par les chercheurs. Cependant l'approche historique de clipedia-txt.net peut faciliter l'approche de cette complexité par les enseignants et étudiants.

Symboles scientifiques

Via les liens suivants, la lectrice trouvera la signification des symboles et lettres utilisés en sciences :

• table des symboles mathématiques ;
• table des symboles littéraux en mathématiques ;
• usage des lettres grecques en sciences.

Affichage

Concernant l'affichage des symboles mathématiques (problématique illustrée en profondeur dans la section suivante, consacrée aux fractions) j'ai choisi la voie présentant à mon avis le meileur arbitrage entre simplicité et portabilité : la combinaison opérateurs mathématiques UTF-8 + CSS, plutôt que (par exemple) les balises MathML.

Notation et calculs de fractions

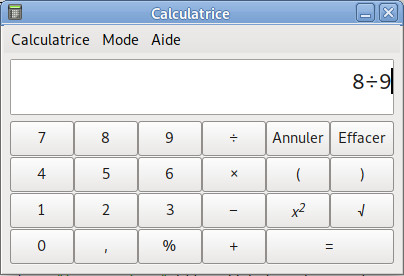
Dans la présente publication nous utilisons le signe " / " pour représenter l'opérateur de division (exemple : 12 / 3 = 4). Comme vous pouvez le constater, il diffère de celui de l'écriture manuscrite : le dénominateur se situe à droite du numérateur plutôt qu'en dessous (notation horizontale plutôt que verticale), et il n'y a qu'une seule longueur possible pour ce signe de division. La notation manuscrite semble à priori plus intuitive, mais est pourtant à l'origine de fréquentes erreurs de calcul chez les étudiants. D'autre part, la notation horizontale des ratios étant celle de la plupart des machines à calculer, il est nécessaire de parfaitement la maîtriser...

Il se fait que Clipedia a réalisé une série de vidéos sur le calcul des fractions. Cette série constitue donc une parfaite entrée en matière ... que nous introduisons par les remarques suivantes.

2 / 2 / 2 =
( 2 / 2 ) / 2 =
1 / 2 =
0,5
Mais :
2 / 2 / 2 ≠
2 / ( 2 / 2 ) =
2 / 1 =
2

N.B. Les parenthèses ne sont pas nécessaire dans le premier cas, mais bien dans le second (pour indiquer que le troisième deux est au dénominateur du second).

Alors que ce problème ne se pose pas pour la multiplication :
2 * 2 * 2 = ( 2 * 2 ) * 2 = 4 * 2 = 8
2 * 2 * 2 = 2 * ( 2 * 2 ) = 2 * 4 = 8

La raison en est que le produit est commutatif, alors que la division ne l'est pas :
4 / 2 = 2
2 / 4 = 0,5

Règle : on lit de gauche à droite, et on ne met des parenthèses que dans deux conditions :

• c'est absolument nécessaire (exemple : ( a + b ) / c ... alors que la notation manuscrite avec barre de division horizontale permet de se passer des parenthèses) ;
• c'est éventuellement utile, pour faciliter la lecture d'une formule complexe.

Quelques développements directs pour s'habituer :

a / b * c =
a * c / b

Ainsi 1 / x * x = 1 puisque :
1 / x * x = x * 1 / x = x / x = 1

a / b / c =
( a / b ) / c =
( a / b ) * ( 1 / c ) =
a / ( b * c )

N.B. Dans le développement ci-dessus, les parenthèses ne sont nécessaires que dans la dernière ligne, pour indiquer que "c" est, comme b, au dénominateur de "a".

a * b / c / a =
b / c

Des difficultés pour comprendre ces égalités ? Alors ce qui suit est faite pour vous...

Pour ne pas commettre les erreurs illustrées dans les vidéos, il importe de bien comprendre ce qu'est une fraction. Pour ce faire, deux approches sont possibles : intuitive et mathématique.

Soit :
N : numérateur
D : dénominateur
Q : quotient
c-à-d :
N / D = Q

Interprétation
intuitive

« Le quotient (Q) est le nombre de fois que ne dénominateur (D) rentre dans le numérateur (N) ».

Démonstration :
N / D = Q   ⇔
N = Q * D

N.d.A. : on notera que, de même, D est le nombre de fois que Q rentre dans N.

Exemple non littéral :
1 / 1 / 2 = 2
car :
2 est le nombre de fois que ( 1 / 2 ) rentre dans 1

Interprétation
mathématique

« Diviser c'est multiplier par l'inverse » : a / b ≡ a * 1 / b. C'est un fait évident, et qu'il est utile de se rappeler pour faire apparaître comme une évidence la résolution de la division précédente par 1/2 : 1 / ( 1 / 2 ) = 1 * 2 (2 est bien l'inverse de 1/2) :

Démonstrations :
a / b =
a * 1 / b / ( b * 1 / b )
or par définition de l'inverse : b * 1 / b = 1  ⇒
a * 1 / b

Exemple non littéral :
1 / ( 1 / 2 ) =
2 * 1 / 2 * ( 1 / 2 ) =
2 / 1 =
2

Nous pouvons ainsi démontrer les trois exemples présentés à la fin de l'introduction de la présente section :

a / b * c =
a * ( 1 / b ) * c =
a * c * ( 1 / b ) =
a * c / b

N.B. Les parenthèse ne sont marquées que pour clarifier : elles ne sont pas ici nécessaires.

a / b / c =
a * 1 / b * 1 / c =
a * 1 / ( b * c ) =
a / ( b * c )

N.B. Les parenthèse sont ici nécessaires, pour indiquer que "c" est au dénominateur de "a".

a * b / c / a =
a * b * 1 / c * 1 / a =
a * b * 1 / ( c * a ) =
a * b / ( c * a ) =
b / c

On notera que les deux derniers exemples opèrent une simplification par réduction du nombre de divisions.

Addition
de fractions

Cette même technique de multiplications est appliquée dans l'addition de fractions, qui requiert d'amener celles-ci à un même dénominateur commun, afin d'additionner "des pommes avec des pommes" :

a / b + c / d =
a * d / ( b * d ) + c * b / ( d * b ) =
( a * d + c * b ) / ( d * b )

Complétons la démonstration en démontrant le passage entre la seconde et la troisième ligne c-à-d que x / y + z / y = ( x + z ) / y :
x / y + z / y =
x * 1 / y + z * 1 / y =
( x + z ) * 1 / y =
( x + z ) / y

De même vous comprenez que :
( a + b ) / b ≠ a
( a + b ) / b ≠ a + 1
car vous comprenez que :
( a + b ) / b =
a / b + b / b =
a / b + 1

L'égalité erronée illustrée dans la première vidéo :
a / b + c / d ≠ ( a + c ) / ( b + d )
résulte du fait que sont additionnés "des pommes avec des poires". Il y a confusion entre somme de fractions et combinaison de proportions. Or, contrairement à la fraction, une proportion n'est pas un nombre.

N.d.A. Soulignons la signification de la nomenclature "numérateur vs dénominateur", qui accorde au second terme une valeur de nature et au premier une simple valeur d'état ("3/4 est un quart à l'état trois"). Cette hiérarchie prend toute sa signification dans la notion de "dénominateur commun".

Fraction
de fraction

Pour interpréter correctement une fraction de fractions il importe de percevoir correctement la hiérarchie des barres de division, qui en écriture manuscrite est déterminée par leur longueur, et dans la présente notation (/) est déterminée au moyen de parenthèses (lorsque nécessaire).

Dès lors qu'une fraction de fractions est correctement interprétée on peut alors la simplifier, en réduisant le nombre de fractions grâce à la propriété évoquées dans les deux vidéos précédentes : « diviser, c'est équivalent à multiplier par l'inverse du dénominateur ». Ainsi diviser par a par b/c, c'est multiplier a par l'inverse de b/c, c-à-d multiplier par c/b :
a / ( b / c ) =
a * ( c / b ) =
a * c / b

On notera également que diviser une première fois par deux (donc multiplier par 1/2), et puis une seconde fois par trois (donc multiplier ensuite par 1/3), cela est équivalent à diviser par 2x3 (c-à-d multiplier par 1/6) :
1 / 2 / 3 =
1 * 1 / 2 * 1 / 3 =
1 * 1 / ( 2 * 3 ) =
1 / ( 2 * 3 ) =
1 / 6

Fraction
négative

Que vaut 3 / ( - 2 ) = ?. La réponse est certes évidente, mais il est frappant de constater que l'interprétation intuitive exposée supra n'est ici plus du tout intuitive : la valeur cherchée ("?") est le nombre de fois qu'un nombre ...négatif rentre dans un nombre positif ...

Cependant la voie mathématique permet de démontrer la réponse. En l'occurrence il s'agit de multiplier par -1 aux numérateur et dénominateur :
3 / ( - 2 ) =
( - 1 ) * 3 / [ ( - 1 ) * ( - 2 ) ] =
- 3 / 2

Voilà, vous êtes maintenant armée pour entrer dans le vif du sujet. Commençons par les fondations : la mesure.