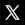III. Géométrie
Du triangle au trapèze
Nous allons montrer que la surface S d'un triangle quelconque vaut :
S(triangle) = ( B * H ) / 2 où :
- B est la base (n'importe lequel des trois côtés) ;
- H est la hauteur correspondant à la base choisie, et qui est telle que (cf. schéma ci-dessous) :
- elle est perpendiculaire à la (droite comprenant la) base choisie ;
- elle va de la base à l'angle opposé à celle-ci (N.d.A. : autrement dit, elle est perpendiculaire à la parallèle à la base passant par cet angle).

N.B. La hauteur n'est pas toujours inscrite dans le triangle. C'est le cas ci-dessus, en raison de l'angle obtu (supérieur à 90°).
On peut démontrer (19) par une expérience de la pensée (cf. illustration ci-dessous), consistant à découper le triangle en tranches horizontales, et à faire tendre leur nombre vers l'infini (et par conséquent leur épaisseur vers zéro), de sorte que leur surface totale correspond à celle du triangle.
Ces tranches peuvent être translatées parallèlement à leur base, et indépendamment les unes des autres, jusqu'à ce qu'elles forment un triangle rectangle de base B et hauteur H. Or, la surface d'un triangle rectangle vaut la moitié du rectangle qu'il détermine.
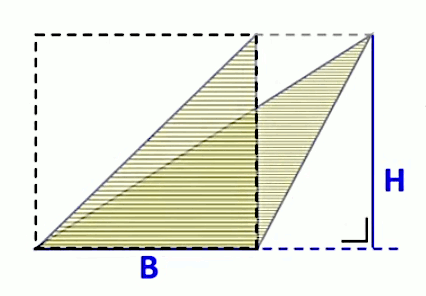
Dès lors que la translation des tranches laisse inchangées leurs longueurs respectives ainsi que leur hauteur, il en résulte que cette transformation du triangle ne modifie pas sa surface. Par conséquent, (19) exprime bien la surface du triangle originel. CQFD.
Une autre démonstration géométrique consiste à intégrer le triangle dans le rectangle de mêmes base b et hauteur h, puis à dessiner la hauteur passant par l'angle qui la définit, puis enfin de constater que celle-ci (hachurée dans schéma ci-dessous) détermine deux sous-rectangles, dont les deux moitiés rouges constituent le triangle. Par conséquent la surface du triangle vaut donc la moitié de celle du rectangle global, soit b * h / 2.

N.d.A. Démonstration algébrique de la surface d'un triangle rectangle
Dans le chapitre /algebre#integrale, nous verrons qu'une démonstration algébrique de (19) consiste à calculer l'intégrale S correspondant, dans le graphique ci-dessous, à la droite passant par les points (0,H) et (B,0) et donc d'équation y(x) = H - H/B * x :
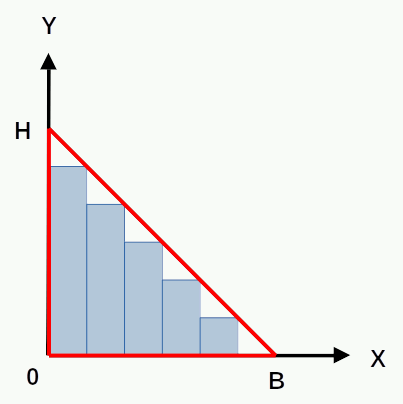
S = ∫ 0 B y(x) * dx ⇔
S = Y(B)- Y(0) ⇔
S = H * ( B - B/2 ) - 0 = B * H / 2
P.S. La première égalité ci-dessus exprime, sur le schéma ci-contre, la somme des produits de la longueur y(x) de n tranches verticales par leur largeur commune dx, lorsque n tend vers l'infini et, partant, dx vers zéro (NB : le symbole "intégrale" ∫ ressemble à un S).
Le parallélogramme est un quadrilatère (une forme fermée composée de quatre côtés) dont ses côtés opposés sont parallèles (et par conséquent de mêmes longueurs).

Nous allons montrer que la surface S d'un parallélogramme vaut :
S(parallélogramme) = B * H où :
- B est la base (n'importe lequel des quatre côtés) ;
- H est la hauteur correspondant à la base choisie, c-à-d la perpendiculaire entre les deux droites parallèles déterminées par la base et son côté opposé.
On peut le démontrer par la même expérience de pensée que pour le calcul de la surface du triangle (cf. supra). En découpant le parallélogramme en tranches horizontales, puis en les translatant horizontalement, on peut transformer le parallélogramme en son rectangle correspondant, de même surface.
Une autre démonstration repose sur la nature symétrique du parallélogramme, qui est composé de deux triangles identiques, déterminés par les axes de symétrie que sont les diagonales du parallélogramme. Par conséquent, la surface du parallélogramme vaut le double de celle de ce triangle, soit :
2 * B * H / 2 = B * H
où la base B du triangle est également un côté du parallélogramme.

B * H / 2 = D * HD / 2
Le trapèze est un quadrilatère comportant une paire de côtés parallèles.
Sa surface vaut S(trapèze) = ( B + b ) * H / 2
où :
B est la grande base du trapèze, b sa petite base, et H sa hauteur.
On démontre cette formule en exploitant le fait que la surface du trapèze vaut la somme des surfaces des deux triangles déterminés par la diagonale du trapèze. Ce calcul est facilité par le fait que de la présence de deux côtés parallèles dans le trapèze implique que la hauteur correspondante est également celle correspondant aux côtés de longueurs respectives b et B des triangles :
S(trapèze) = B * H / 2 + b * H / 2 = ( B + b ) * H / 2

On notera que le parallélogramme (cf. vidéo précédente) est un cas particulier de trapèze dont les deux bases sont d'égales longueurs. Ainsi il résulte de (21) que :
S(parallélogramme) = B * H / 2 + B * H / 2 = 2 * B * H / 2 = B * H
Théorème de la médiane
Comment tracer un cercle en utilisant une équerre plutôt qu'un compas ?
Réponse en quatre étapes :
- Préparer les points fixes : planter deux clous (ou marquer deux points fixes) sur une surface plane, séparés par la longueur du diamètre du cercle souhaité.
- Positionner l'équerre : caler l'équerre contre les deux clous, ceux-ci étant situés à l'intérieur de l'équerre, par exemple en posant un côté de l'équerre contre les deux clous (cf. début de l'animation ci-dessous).
- Tracer un demi-cercle : après avoir fixé un crayon à l'intersection de l'angle droit (⇒ dans l'exemple ci-dessus, il pointe alors sur un des deux points fixes), faire pivoter l’équerre, en veillant à maintenir le contact entre ses deux bords perpendiculaires et les clous. La pointe du crayon va alors dessiner un demi cercle dont le diamètre est la distance entre les deux clous.
- Tracer l'autre demi-cercle.. Pour obtenir un cercle entier, répéter les opérations 2 et 3 en inversant la position de l’équerre.

Pour expliquer ce phénomène, nous allons invoquer la notion de médianes d'un triangle, c-à-d les trois droites passant par l'intersection d'un angle et le milieu du côté opposé. On peut démontrer (mais on ne le fera pas ici) que ces médianes se croisent en un même point.

Les trois médianes d'un triangle quelconque se coupent en un même point.
Pour démontrer le théorème de la médiane, nous allons considérer la médiane de l’hypoténuse (de longueur h) d'un triangle rectangle. Si, partant du centre de l'hypoténuse, on trace deux droites perpendiculaires aux deux autres côtés, on obtient deux triangles rectangles identiques, et dont les hypoténuses (de longueur h/2) correspondent aux deux moitiés de hypoténuse du grand triangle rectangle.

On peut en déduire que les deux perpendiculaires passant par le milieu de l'hypoténuse (i) coupent les cotés opposés en leur milieu, et (ii) constituent par conséquent un axe de symétrie autour duquel chacun des triangles rectangles correspondant peut pivoter à 180° pour confondre son hypoténuse h/2 sur la médiane de longueur m. Par conséquent m = h/2. On a ainsi démontré le théorème de la médiane (dans un triangle rectangle) : « dans un triangle rectangle, la longueur de la médiane relative à l'hypoténuse vaut la moitié de celle-ci ».
Autrement dit, la médiane de l'hypoténuse d'un triangle rectangle est le rayon d'un cercle dont cette hypoténuse est un diamètre.

Il en découle le corollaire que « des triangles rectangles qui partagent la même hypoténuse ont tous le sommet de leur angle droit sur un unique cercle, pour lequel l'hypoténuse constitue un diamètre. ».

C'est bien ce résultat que reproduit la méthode proposée plus haut pour dessiner un cercle avec une équerre qui pivote autour des deux extrémités d'un diamètre de ce cercle.

Le théorème réciproque du théorème de la médiane (pour un triangle rectangle) permet de déterminer que « un triangle est rectangle si la médiane de son plus grand côté vaut la moitié de celui-ci ».
On peut le démontrer géométriquement en montrant que si la médiane relative au plus grand côté d'un triangle vaut la moitié de ce côté, alors la rotation de ce triangle autour de l'axe de symétrie constitué par l'hypoténuse forme nécessairement un rectangle, ce qui implique que le triangle pivoté est un triangle rectangle.

Partant d'un parallélogramme quelconque dont une diagonale vaut L, si l'on ramène l'autre diagonale à cette même longueur L, le parallélogramme devient rectangle.
Théorème de Thalès
Le théorème de Thalès, dont nous verrons les nombreuses applications, énonce un fait assez intuitif : une droite parallèle à l'un des côtés d'un triangle (BD dans le schéma ci-dessous) définit, avec les droites des deux autres côtés, un nouveau triangle (ABD) dont les côtés sont proportionnels à ceux du premier (ACE).
N.d.A. Le triangle dérivé pourrait évidemment être le plus grand ...
Autrement dit, le rapport entre côtés homologues du petit et du grand triangle est constant.

N.d.A. Ainsi ces deux triangles (le grand ACE et le petit ABD) sont dit "semblables", car ils ne diffèrent que par leur taille. Une expression du théorème de Thalès est donc que « le rapport entre côtés homologues de triangles semblables est constant ».
L'animation suivante illustre ces égalités de proportions, de façon intuitive. On dessine la section parallèle (h), puis la perpendiculaire (C) aux deux droite parallèles, de sorte que l'on obtient deux couples de triangles rectangles équivalents (parties supérieure et inférieure).

Il est alors plus facile (cf. schéma suivant) de percevoir intuitivement que dans chacun de ces deux couples, le rapport entre côtés homologues du petit et du grand triangle est constant :
dans le couple de triangles supérieur, la droite parallèle h1 détermine deux triangles rectangles équivalents tels que c / C = r = e / E
dans le couple de triangles inférieur, la droite parallèle h2 détermine deux triangles rectangles équivalents tels que c / C = r = l / L

Nous avons donc r = c / C = e / E = l / L. Reste à traiter le cas de h / H, ce que l'on fait par un système de trois équations :
h1 = r * H1
h2 = r * H2
h = h1 + h2
⇒ en substituant les deux premières égalités dans la troisième :
h = r * H1 + r * H2 ⇔
h = r * ( H1 + H2 ) ⇔
h = r * H ⇔
r = h / H
Soulignons que ces développements ne constituent pas une démonstration rigoureuse mais une illustration intuitive, fondée sur la réduction de la problématique au cas de deux triangles rectangles, le triangle rectangle permettant une illustration relativement intuitive de la notion de proportionnalité.
Le cadre conceptuel du théorème de Thalès repose sur les cinq points d'intersection créés par quatre droites dans un plan. Deux de ces droites sont parallèles, tandis que les deux autres ne le sont pas (droite "sécantes").
Ces cinq intersections déterminent deux triangles semblables, c-à-d dont leur seule éventuelle différence est la surface (d'où les expressions de "grand" et "petit" triangles semblables déterminés par ces quatre droites).
Dans la précédente vidéo, nous avons montré que la démonstration du théorème est composé de deux parties, concernant les côtés homologues de ces deux triangles semblables :
- les rapport entre les 2x2 côtés homologues situés sur les droites sécantes sont égaux;
- le rapport entre les 2 côtés homologues situés sur les deux droites parallèles est égal aux deux précédents rapports.
Nous allons ici démontrer la première égalité, c-à-d celle concernant les 2x2 côtés homologue situés sur les droites sécantes.
Cette démonstration, proposée par Euclide (≈ 300 av. J.C.), consiste en trois étapes :
dans le parallélogramme déterminé par les quatre intersections déterminées par les deux droites parallèles, les deux diagonales déterminent deux triangles de même base (c) et hauteur (h), et donc de même surface (SA = SB) :

on calcule alors cette surface de deux autres façons, en utilisant comme bases respectives celles situées sur les droites sécantes :
( A - a ) * hA / 2 = ( B - b ) * hB / 2
enfin, pour se débarrasser de hA et hA, on calcule leurs valeurs respectives, en exprimant la surface du petit triangle semblable (S) en fonction de ces deux hauteurs :
S = a * hA / 2 = b * hB /2 ⇔
hA / 2 = S / a
hB / 2 = S / b
que l'on substitue dans l'équation du point 2 ⇒
( A - a ) * S / a = ( B - b ) * S / b ⇔
A / a = B / b ⇔
a / A = b /B
CQFD
Exercice (N.d.A.). Visualiser la démonstration en prenant cette fois la grande section parallèle (C) comme base des deux triangles de même surface. Constater que dans ce cas, on se débarrasse des deux nouvelles hauteurs en exprimant cette fois la surface du grand triangle semblable en fonction de celles-ci. Enfin, refaire les deux visualisations dans le cas où l'intersection de deux droites non parallèles se situe cette fois entre les deux droites parallèles (configuration dite "en papillon" du théorème de Thalès). Conclusion : ce système de 2x2 droites (2 parallèles, 2 sécantes) dans un plan est donc caractérisé par une certaine symétrie (même si la symétrie géométrique n'y est pas nécessairement parfaite).
Le théorème de Thalès (cf. supra #Thales) conduit à la notion de triangles semblables, qui est très utile pour résoudre divers types de problèmes.
La configuration de Thalès (deux droites sécantes coupées par deux droites parallèles) correspond à deux triangles (A,B,C) et (a,b,c) dits "semblables", c-à-d (cf. schéma infra) :
- tels que les rapports des côtés homologues sont égaux:
a / A = b / B = c / C = r (où r est appelé "rapport de similitude") ; - ou encore tels que les angles homologues sont égaux, puisque :
- les angles bleu-vert sont déterminés par deux parallèles (bleues) à une même droite (verte) ;
- les angles bleu-rouge sont déterminés par deux parallèles (bleues) à une même droite (rouge) ;
- le troisième triangle (vert-rouge) est commun au deux triangles.

C'est dans l'équivalence de ces deux approches corollaires – égalité des rapports des côtés homologues et égalité des angles homologues, de deux triangles semblables – que réside l'aspect pratique du théorème de Thalès : si l'une de ces deux égalités est vérifiée, alors l'autre peut en être déduite.
D'autre part, un autre corollaire de l'égalité des rapports des côtés homologues de triangles semblables :
a / A = b / B = c / C = r
est l'égalité des rapports des côtés d'angles homologues :
a / A = b / B ⇔ a / b = A / B
a / A = c / C ⇔ a / c = A / C
b / B = c / C ⇔ b / c = B / C
C'est sur base de ces corollaires que le théorème – qui fut démontré par Euclide (cf. section précédente) – fut attribué (plus tard) à Thalès, qui l'aurait utilisé pour calculer la hauteur de la pyramide de Khéops, à partir de la mesure de son ombre et de celle d'un piquet planté à proximité.

La configuration du schéma ci-dessus est bien celle du théorème de Thalès : le sol et les rayons solaires correspondent aux deux sécantes, et les deux hauteurs aux deux parallèles.
Et l'on constate en effet que (i) les deux angles rouge-vert déterminés par le sol et les rayons du soleil sont identiques, dans la mesure où l'on peut considérer les rayons du soleil parallèles et le sol plat ; (ii) les angles bleu-rouge correspondant aux hauteurs sont droits et donc égaux ; (iii) les angles bleu-vert sont également identiques puisque leurs droites composantes sont parallèles.
On peut donc en déduire l'applicabilité du corollaire ci-dessus, et ainsi calculer la hauteur H de la pyramide :
H / L = h / l ⇔
H = h / l * L
Il reste alors à mesurer :
la longueur (l dans le schéma ci-dessous) de l'ombre portée par un piquet (de hauteur h) planté à proximité de la pyramide ;
la longueur de l'ombre de la pyramide, augmentée de la moitié de sa base (L).
Nous allons ici montrer comment le théorème de Thalès permet de déterminer la distance à laquelle placer un objet que l'on veut photographier avec un appareil photo dont le système de mise au point serait inopérant.
Mais commençons par montrer le fonctionnement d'un appareil photographique. Dans le schéma suivant, la bougie photographiée est à gauche. La distance do qui la sépare de la lentille de l'appareil est appelée "distance objet". La distance di entre la lentille et le point de convergence des rayons est appelée "distance image".

L'animation ci-dessus montre que la mise au point consiste à faire en sorte que la surface d'impression de l'image dans l'appareil se situe au point de convergence des rayons, c-à-d à la distance image di.
N.d.A. La "distance focale" f dépend des caractéristiques de la lentille (courbure des rayons et indice de réfraction). Si la distance image est égale à la distance focale (di = f), cela signifie que l'objet est situé à une très grande distance, de sorte que les rayons sont quasiment parallèles (c'est le cas, par exemple, pour la lumière provenant d'étoiles). Pour approfondir les principes élémentaires de l'optique (et comprendre notamment pourquoi l'image de la bougie est à l'envers et plus petite) cf. /action-a-distance#optique.
Si le système de mise au point de l'appareil est inopérant par le fait qu'il est impossible d'adapter la distance de la surface d'impression à la distance image di, alors il faut faire l'inverse, c-à-d fixer la distance objet do de telle sorte que le point de convergence des rayons lumineux (la distance image di) corresponde à la distance de la surface d'impression. Ainsi le schéma suivant montre qu'en rapprochant la bougie de la lentille, la pente du rayon passant par le centre augmente, de sorte que son intersection avec le rayon d'origine horizontale se fait plus loin, là ou est bloquée la surface d'impression.

C'est ici que le théorème de Thalès permet de calculer cette valeur de do. L'animation suivante montre que la méthode consiste à repérer, dans la représentation schématique supra, deux configurations "en papillons" du théorème de Thalès :
- l'une de longueur do+di, et dont le noeud est le centre de la lentille;
- l'autre de longueur di, et dont le noeud est le point de focale ou "foyer" de focale.

On peut alors appliquer, pour chacune des deux configurations, le principe d'égalité des rapports des côtés homologues (22), et ainsi obtenir un système de deux équations à deux inconnues ( do et hi ) :
- configuration papillon de largeur do+di :
ho / hi = do / di - configuration papillon de largeur di :
ho / hi = f / ( di - f )
De sorte que :
do / di = f / ( di - f ) ⇔
do = f / ( di - f ) * di ⇔
do = di * f / ( di - f )
Ainsi, par exemple, si :
• f = 5 cm
• la surface d'impression de l'appareil est bloquée à 7 cm, et que par conséquent on souhaite que di = 7 cm
⇒
do = 7 * 5 / ( 7 - 5 ) = 35 / 2 = 17,5 cm
Cette application du théorème de Thalès concerne la mécanique. Le schéma suivant représente un conducteur poussant, le long d'une pente de 12 % de déclivité, sa voiture de masse 500 kg, tombée en panne. Avec ces seules données, les théorèmes de Thalès et de Pythagore vont nous permettre de calculer la force minimale que doit exercer le conducteur pour pousser sa voiture (qui est la force qu'elle exerce sur lui – loi d'action-réaction, ou "troisième loi de Newton" (cf. /dynamique#chute-des-corps) – et dont la direction est parallèle à la route).
Une masse de 500 kg correspond à un poids de 500 kg-force (aussi noté kg'), en vertu de la seconde loi de Newton : F = m * a (cf. /dynamique#loi-newton).
Une déclivité de x % signifie que pour s'élever de x mètres, il faut parcourir une distance de 100 mètres, horizontalement (et non le long de la pente comme cela est affirmé erronément dans la vidéo) [source]. Autrement dit la déclivité est l'inclinaison de l'hypoténuse de ce schéma, et sa mesure correspond à la tangente de l'angle que fait l'hypoténuse avec l'axe horizontal (47).
Le schéma illustre le fait que tout corps subit son propre poids, qui est de direction verticale et orientée vers le bas. C'est la force de gravitation P = m * g (où g est l'accélération due à la gravitation, soit environ 9,81 m/s2 sur Terre). On peut la décomposer en deux forces d'action-réaction (perpendiculaires) :
entre la voiture et la pente sur laquelle elle repose, cette force étant perpendiculaire à la pente ;
entre la voiture et le pousseur, c-à-d la force qu'il doit exercer pour que le véhicule ne descente pas la pente (NB : on fait abstraction des forces de frottement), et qui est la projection orthogonale de la force de gravitation dans la direction de la force de réaction de la route sur la voiture.

Apparaissent alors deux triangles rectangles (schéma ci-dessus) :
le grand (dans ce schéma), dont l’hypoténuse correspond à la pente ;
le petit (dans ce schéma), dont l’hypoténuse correspond à la direction de la force de gravitation.
Ces deux triangles sont semblables car :
- leurs petits angles adjacents à l'angle droit sont égaux, car leur côtés sont perpendiculaires deux à deux ;
- leurs grands angles adjacents à l'angle droit sont égaux, car leur côtés sont parallèles deux à deux.
On peut donc placer ces deux triangles dans une configuration de Thalès :

Dans certains cas, pour placer deux triangles semblables en configuration de Thalès, la seule rotation dans le plan ne suffit pas : il faut la combiner avec un retournement dans l'espace à trois dimensions.
Il nous suffit alors d'appliquer la règle de Thalès : les rapports des côtés homologues sont égaux (22) ⇒
H / F = D / P
où D est la longueur de la pente, donnée par le théorème de Pythagore (23) : √(1002+122)≈100,7 m ⇒
F = H / D * P ≈ 12 / 100,7 * 500 = 59.6 kg'
Théorème de Pythagore
Théorème de Pythagore : dans un triangle rectangle :
R2 = x2 + y2 : "le carré de l'hypoténuse (R) vaut la somme du carré des deux autres côtés du triangle (rectangle)".
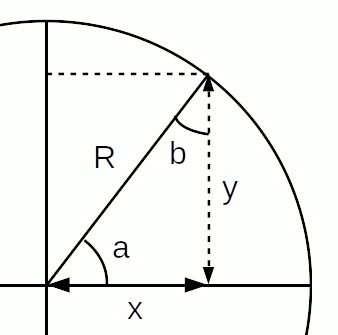
Nous verrons une démonstration algébrique du théorème de Pythagore dans la section consacrée au produit scalaire (60).
Historiquement, le théorème de Pythagore fut d'abord démontré géométriquement. Voici l'une des ces démonstrations visuelles (cf. schéma ci-dessous) :
la première des trois parties du schéma illustre la rotation d'un triangle rectangle d'hypoténuse R, autour du coin supérieur gauche du carré bleu ;
dans la première des quatre positions du triangle, le petit côté adjacent de son hypoténuse correspond au côté inférieur du carré rouge (de surface x2), et le grand côté adjacent de son hypoténuse correspond au côté gauche du carré bleu (de surface y2) ;
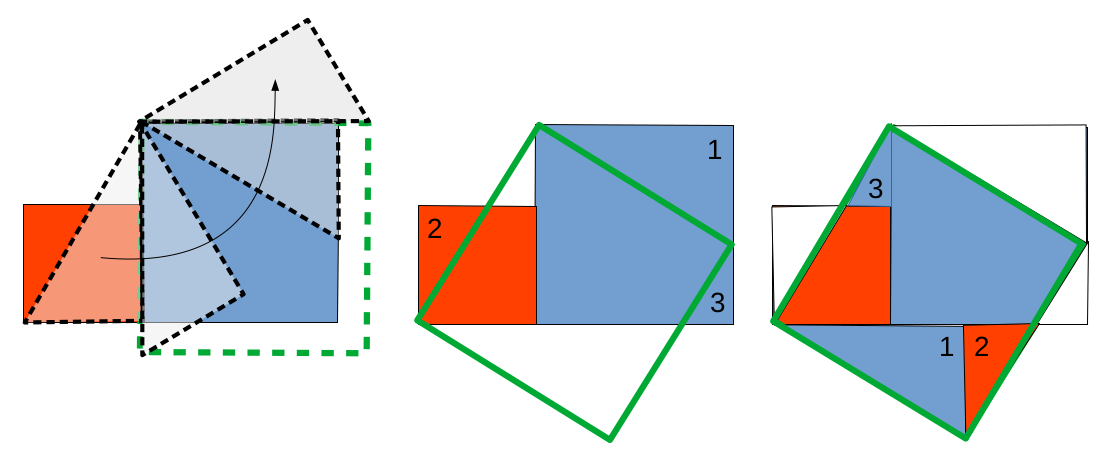
à l'hypoténuse du triangle correspond un carré vert de surface R2, qui peut pivoter autour du même point que le triangle ;
la partie 2/3 du schéma, suggère que la somme des trois surfaces colorées situées à l'extérieur de R2 (1, 2, et 3) correspondent à la surface totale des deux aires blanches de R2, ce que confirme la partie 3/3 du schéma ;
on a ainsi démontré que la surface du carré vert, c-à-d le carré de l'hypoténuse du triangle, est bien égal à la somme des carrés rouge et vert, c-à-d à la somme des carrés des deux autres côtés du triangle rectangle : R2 = x2 + y2.
N.d.A. Voila qui illustre que la géométrie est un lien entre la réalité physique et l'abstraction mathématique. Ainsi cette démonstration expérimentale, que l'on peut réaliser physiquement avec des bouts de papier, peut être confirmée mathématiquement, c-à-d de façon abstraite (cf. infra (60) ).
N.d.A. On constate que le théorème de Pythagore est l'équation d'un cercle de rayon R, et centré sur le point (0,0) :
R2 = x2 + y2 ⇔
y = +/- √(R2 - x2)
Et l'on obtient l'équation pour un cercle centré sur un point quelconque (a,b) en remplaçant x par x-a et y par y-b :
R2 = ( x - a )2 + ( y - b )2 ⇔
y = +/- √( R2 - ( x - a )2 ) + b
Le nombre pi et le cercle
• Aire du cercle
Le nombre "pi ", noté π, est la valeur (constante) du rapport entre le périmètre (P) d'un cercle et son diamètre (D) : π = P / D.
π est l'équivalent de la lettre P dans l'alphabet grec, première lettre du mot "périmètre".
- Le périmètre d'un cercle porte le nom spécifique de circonférence.
Interprétation. Autrement dit, le nombre π :
- est la circonférence d'un cercle dont le diamètre vaut une unité de longueur (D=1) ;
- est le nombre de fois que la longueur du diamètre D s'inscrit dans celle de la circonférence P.
Ce ratio est donc universel : il concerne les cercles de toute taille.
La valeur exacte de π est inconnue car π est un nombre "irrationnel" et "transcendant" :
- irrationnel signifie qu'il ne peut pas être exprimé comme une fraction de deux nombres entiers. Sa représentation décimale est infinie et non périodique, c'est-à-dire qu'il n'y a jamais de répétition dans les décimales de π. Ainsi π commence par 3,14159... (≈ 3,142) mais il continue indéfiniment sans suivre de schéma régulier.
- transcendant signifie qu'il ne peut pas être la solution d'une équation algébrique à coefficients entiers (comme une équation du type a * xn + b * xn-1 + ... + k = 0).
Même si nous ne connaissons pas la valeur exacte de π, les savants ont développé, dès l'antiquité, des méthodes extrêmement précises pour calculer ses premières décimales. Aujourd'hui, avec les ordinateurs, on a pu calculer des milliers de milliards de décimales de π, bien plus que nécessaire pour toute application pratique (comme en ingénierie ou en physique).
Une de ces méthodes consiste à approcher le cercle par un polygone, dont le nombre de faces peut être augmenté à volonté, selon la précision de π que l'on veut obtenir. Dès l'antiquité, Archimède a découvert une méthode (complexe) valable pour n'importe quel nombre de côtés, donc pour un polygone qui se rapproche du cercle autant que nécessaire. Nous allons ici montrer ce principe dans le cas simple d'un polygone à six côtés (c-à-d un hexagone), inscrit dans un cercle de diamètre D (cf. schéma suivant). Nous pourrons ainsi calculer une valeur minimale de π : il est en effet intuitif, à la vue du schéma ci-dessous, que le périmètre de l'hexagone est inférieur à celui du cercle qui l'entoure (considérons un côté : la ligne droite entre deux point est plus courte que n'importe quelle courbe entre ces deux points).

L'animation suivante montre que, l'hexagone étant composé de triangles équilatéraux ⇒ chaque côté de ces triangles vaut D/2 ⇒ le périmètre de l'hexagone vaut Ph = 6 * D / 2 = 3 * D.

Par conséquent, le périmètre P du cercle qui entoure l'hexagone est tel que P > 3 * D.
Le schéma suivant montre que, selon le même principe, le diamètre D du cercle est égal au côté du carré qui l'entoure ⇒ on peut en déduire que le périmètre du cercle est tel que P < 4 * D.

Résumons : 3 * D < P < 4 * D. Et le schéma suivant suggère que la circonférence P est plus proche du périmètre de l'hexagone (3D) que de celui du carré (4D).

Pour obtenir une mesure plus précise, sans recourir à la méthode complexe d'Archimède, on peut réaliser une expérience (cf. animation ci-dessous) afin de calculer π = P / D, en mesurant le diamètre D d'une roue, et le déroulement de sa circonférence P.

Lecture : constatez (i) le déroulement du cercle rouge (P) entourant la roue de diamètre D=1 ; (ii) le losange bleu retrouve le rouge après un tour de roue, ou encore à une distance π [source].
On obtiendra une valeur proche de celle calculée, de façon nettement plus précise, par Archimède.
On ne peut exprimet π sous forme de ratio, mais un ratio proche de π est 22 / 7 = 3,1428... ≈ 3,143 (soit une différence avec deux zéros après la virgule). N.d.A. : avec l'aide de ChatGPT, j'ai conçu ce script Python qui permet de trouver des ratios avec plus de zéros après la virgule (notamment six zéros après la virgule, avec 355 / 113) ... et de constater que le temps de calcul de l'ordinateur augmente assez rapidement avec le degré de précision souhaité (sur ma machine, de 2 sec. à 20 sec. entre x=7 et x=8). Pour approfondir, voir fr.wikipedia.org/wiki/Approximation_de_π.
Applications. Les applications de π sont nombreuses en géométrie, dans toutes sortes de calcul de périmètres, surfaces et volumes, que nous allons développer ...

Le nombre π intervient également dans de nombreuses mesures de physique :
- mécanique (N-E dans illustration ci-dessous) : calcul de la vitesse v de défilement d'un disque de diamètre D et effectuant un tour en un temps T ;
- magnétisme (S-E) : calcul du champ en fonction de la distance par rapport au courant électrique ;
- électricité (N-O) : calcul de la force électrique entre deux charges électriques ;
- mécanique quantique (S-O): expression mathématique du principe d'incertitude dans le cas d'un photon (particule de lumière). ;

Dans la vidéo précédente on a évoqué le fait que dès l'antiquité, des savants ont découvert qu'il existe un rapport constant entre le périmètre et le diamètre du cercle – π = P / D – et que l'on peut facilement en mesurer une valeur approximative.
À cette époque, Archimède a découvert une méthode permettant, non plus de mesurer, mais de calculer π, avec autant de précision que souhaité. Elle consiste à approcher le cercle par un polygone dont le nombre de côté peut être arbitrairement élevé.
Nous allons montrer ici que cette méthode permet également de déterminer la formule du périmètre du cercle, et puis celle de sa surface.
Périmètre
Pour déterminer la formule du périmètre, la première étape consiste à approcher le cercle par un simple hexagone. Or celui-ci a pour propriété d'être composé de six triangles équilatéraux, de sorte que les côtés de ces angles sont également le rayon R du cercle entourant l'hexagone (cf. schéma infra). Ce rayon vaut évidemment la moitié du diamètre :
R = D / 2 ⇔
D = 2 * R
substitué dans la formule du périmètre du cercle en fonction de son diamètre :
P = π * D (25) ⇒
le périmètre du cercle en fonction du rayon vaut :
P = 2 * π * R

Surface
Pour déterminer la formule de la surface du cercle, la première étape consiste à calculer la surface de l'hexagone contenu dans le cercle. Le schéma suivant montre qu'il suffit pour cela de recomposer l'hexagone en joignant horizontalement ses parties supérieure et inférieure, de sorte que l'on obtient un parallélogramme, dont la surface est tout simplement le produit de la base (3 * R) par la hauteur (h) [cf. (20)].

N.d.A. Pour plus de clarté, nous allons infra noter S par Sp, et P par Pp.
D'autre part, on peut voir dans le schéma ci-dessous que le périmètre de l'hexagone vaut 6 * R, soit deux fois la base du parallélogramme :

Pp = 6 * R = 2 * ( 3 * R ) ⇔
3 * R = Pp / 2
substitué dans :
Sp = 3 * R * h ⇒
Sp = Pp / 2 * h
On a ainsi exprimé la surface de l'hexagone non plus en fonction du rayon du cercle mais du périmètre de l'hexagone (qui approche celui du cercle) et de la hauteur h du parallélogramme correspondant. On pourrait calculer h grâce au théorème de Pythagore (23), mais nous n'allons pas emprunter cette voie. Nous allons plutôt exploiter un fait visuellement évident dans le schéma suivant : R est plus grand que h, mais lorsque l'on augmente le nombre de faces du polygone, la longueur R se rapproche de la longueur h.

On peut alors appliquer la méthode imaginée par Archimède, c-à-d augmenter "à l'infini" le nombre des triangles (qui ne sont plus équilatéraux mais isocèles), de sorte que :
le rayon R du cercle tend vers la hauteur h du parallélogramme ⇒ on peut alors, dans la formule exprimant la surface du parallélogramme (donc du polygone), remplacer h par R ⇒ Sp ≈ Pp / 2 * R ;
corrélativement, la base de ces triangles isocèles tend vers zéro ⇔ le périmètre du polygone tend vers celui du cercle ⇒ on peut alors, dans l'approximation ci-dessus de Sp, remplacer Pp par P = 2 * π * R (26), et Sp par S ⇒
la surface du cercle vaut : S = π * R2
N.B. Alors que le périmètre du cercle P = 2 * π * R (26) est fonction de R (en mètres), sa surface S = π * R2 (27) est logiquement fonction de R2 (en mètres carrés). D'autre part, dans le premier cas la valeur 2 est en facteur, alors que dans le second elle est en exposant.
Conclusion : par cette d'approche combinant l'infiniment grand (le nombre des triangles isocèles constituant le polygone approchant le cercle) et l'infiniment petit (les bases ces triangles, dont la somme approche le périmètre du cercle), Archimède a posé les bases du calcul infinitésimal.
N.d.A. Soulignons ainsi – en anticipation du chapitre /algebre#integrale-theorie – que le périmètre est la dérivée de la surface du cercle :
Soit S(r) = π * r2 ⇒ dS / dr = 2 * π * r
c-à-d, "à rebrousse-poil", que la surface peut être calculée par intégration infinitésimale du périmètre :
S(R) = ∫0R 2 * π * r * dr = π * R2
(103).
Le cône
• Volume

Un cône est entièrement caractérisé par sa hauteur H et son rayon R. La formule de sa surface sera donc fonction de ces deux grandeurs.
Commençons par souligner que le cône est une surface réglée, c-à-d composée de droites (à l'instar du cylindre). En l'occurrence chacune de ces droites passe par la pointe du cône et un point du périmètre de sa base.
On peut ainsi décomposer la surface du cône en une somme de "presque triangles". "Presque" car ces surfaces d'apparence triangulaire ont une base courbée. Cependant on peut toujours découper la surface du cône en un nombre suffisamment grand de ces "presque triangles", de sorte que leur base b devient infinitésimale et peut alors être considérée comme "presque droite". Dans ces conditions, la surface des "presque triangles" peut être approximée par la surface du triangle s = b * h / 2 (19).

N.B. Ne pas confondre la hauteur H du cône avec sa longueur h (qui est aussi la hauteur des triangles).
Décomposition infinitésimale. Selon le même principe, alors que la surface de l'océan est clairement sphérique, la surface de l'eau d'une surface relativement infinitésimale, telle que celle d'une piscine, peut être considérée comme "presque plane" : sa courbure est imperceptible pour l'oeil d'un humain. P.S. : l'analogie s'arrête ici car, comme nous verrons plus loin, contrairement à la sphère, le cône est une surface développable.
Soulignons ici la distinction entre la hauteur H du cône et sa longueur h, qui n'est autre que l'hypoténuse du triangle rectangle dont les deux autres côtés sont de longueur H et R (cf. schéma ci-dessous), de sorte que la valeur de h est donnée par le théorème de Pythagore : h = √ ( H2 + R2 ) (23)

En substituant h = √ ( H2 + R2 ) dans s = b * h / 2 on peut alors exprimer la valeur de la surface de chaque triangle plan en fonction des grandeurs H et R déterminant le cône :
s = b * √( H2 + R2 ) / 2
⇒ soit N le nombre de "presque triangles" composant la surface S du cône, alors celle-ci vaut :
S = N * b * √( H2 + R2 ) / 2
Or N * b n'est autre que le périmètre de la base du cône, soit P = 2 * π * R (25)
de sorte que la surface du cône vaut finalement :
S = 2 * π * R * √( H2 + R2 ) / 2 ⇔
S = π * R * √( H2 + R2 )
CQFD
Une autre démonstration repose sur le développement de la surface conique en une surface plan (N.B. : le cône est une surface développable).

N.d.A. On devine ici qu'il est facile, une fois déployée la couverture d'un tipi, de l'enrouler autour d'un axe, ce qui facilite son transport.
Notez que la longueur de l'arc du "morceau de tarte" (le terme mathématique est plutôt "secteur circulaire") que constitue le cône déployé vaut évidemment la longueur du périmètre de la base du cône, soit 2 * π * R (NB : R est le rayon de la base du cône, tandis que le rayon du secteur circulaire est h). Et par conséquent, la surface développée constitue seulement un secteur du cercle car :
R < h ⇒
2 * π * R < 2 * π * h

Observons maintenant la relation entre le secteur circulaire (d'arc 2 * π * R) et son cercle (de rayon h). Le rapport entre les longueurs de l'arc de cercle (2 * π * R) et de la circonférence (2 * π * h) est logiquement le même qu'entre les surfaces du secteur circulaire (S) et de son cercle (π * h2) :
2 * π * R / 2 * π * h = S / π * h2 ⇔
S = π * R * h
qui exprime donc la surface du cône en fonction de son rayon et de sa longueur h, plutôt qu'en fonction de son rayon et de sa hauteur H.
Commençons par raisonner dans l'espace à deux dimensions, où l'on constate cette relation simple entre triangle et rectangle de mêmes bases et hauteurs : l'aire du triangle (cf. supra #triangle-trapeze) vaut alors la moitié de celle du rectangle

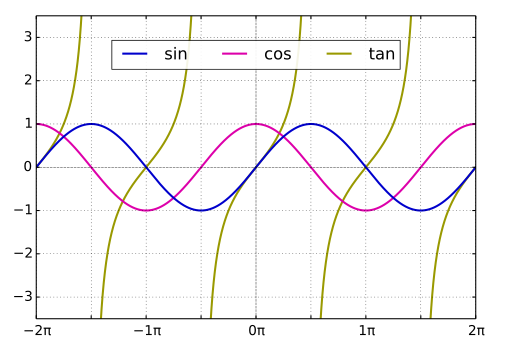
Aparté. La seconde étape de la démonstration est un aparté (auquel nous reviendrons évidemment plus loin) : comment calculer la somme des nombres de 1 à N (1 + 2 + 3 + ... + n + ... + N), que l'on formule mathématiquement sous la forme d'une suite arithmétique ∑n=1N n = ?
Le chapitre infra /algebre#suites-mathematiques répond à cette question de façon algébrique, mais nous allons ici le faire par une méthode géométrique. Celle-ci consiste à représenter une unité algébrique par une unité géométrique sous la forme d'un petite surface carrée. Les nombres de la suite sont alors alignés verticalement dans une grille de NxN unités géométriques.

N = 10.
On constate alors que la surface totale de la suite des petits carrés semble correspondre à la moitié de la surface de la grille carrée. Enfin presque, car si l'on compare le bord en escalier de ce presque triangle avec la diagonale passant par les coins N-E et S-O du carré, on constate que le triangle vaut la moitié du carré ...plus N demi-carrés, soit N/2 petits carrés. On peut alors poser que notre suite arithmétique vaut la moitié de la surface de la grille plus N/2 :
∑n=1N n = N2 / 2 + N / 2
N.d.A. L'erreur d'approximation vaut :
( N / 2 ) / ( N 2 / 2 ) = 1 / N
et diminue donc lorsque N augmente.
Il est facile de visualiser que si l'on diminue la surface des petits carrés, on peut alors placer plus de ces unités géométrique dans la même grille. Et plus on diminue la taille des ces unités en augmentant leur nombre, plus le bord en escalier du triangle se confondra avec la diagonale de la grille carrée, de sorte que la surface du presque triangle approchera celle de la moitié de la grille carrée c-à-d N2 / 2 ⇒
∑n=1N n ≈ N2 / 2
N.d.A. Le paragraphe suivant diverge quelque peu de la vidéo par son approche plus algébrique que géométrique.
Et lorsque N tend vers l'infini, le terme N / 2 du membre de droite de :
∑n=1N n = N2 / 2 + N / 2
devient insignifiant relativement au terme N2/ 2, ce que l'on peut démontrer algébriquement comme suit :
∑n=1N n = N2 / 2 + N2 / 2 / N ⇔
∑n=1N n = N2 / 2 * ( 1 + 1 / N ) ⇒
limN→∞ [ ∑n=1N n ] = limN→∞ [ N2 / 2 * ( 1 + 1 / N ) ] ⇒
limN→∞ [ ∑n=1N n ] = N2 / 2
Le volume. Cet aparté étant terminé, revenons au calcul du volume du cône. Nous allons utiliser la méthode géométrique proposée par Archimède au III° siècle av. J.C., qui consiste à assimiler le cône à une pile de N cylindres, dont le rayon diminue en fonction de la hauteur H du cône. Il est alors visuellement intuitif que :
- la hauteur de chaque cylindre vaut H / N
- la somme des largeurs des N marches vaut R (rayon du cône) ⇒ cette largeur vaut R / N.

Il ne nous reste alors plus qu'à calculer la somme des volumes de ces cylindres, pour obtenir une approximation du volume du cône, celle-ci étant d'autant plus proche de la valeur réelle que N sera grand :
- largeur des marches : limN→∞ ( R / N ) = 0
- hauteur des marches : limN→∞ ( H / N ) = 0
Puisque le rayon du cylindre situé au sommet vaut logiquement R / N, alors le rayon du cylindre de rang n vaut n * R / N, de sorte que son volume vaut :
Vn = π * ( n * R / N )2 * H / N ⇔
Vn = π * R2 * H / N3 * n2
La somme des volumes des N cylindres se formule alors algébriquement comme suit :
VN = ∑n=1N Vn ⇒
VN = ∑n=1N π * R2 * H / N3 * n2 ⇔
VN = π * R2 * H / N3 * ∑n=1N n2
Mais que vaut le facteur ∑n=1N n2 ? Pour répondre à cette question, nous allons nous inspirer de l'aparté supra, où nous avions montré, avec la méthode d'alignement d'unités géométriques, que ∑n=1N n ≈ N2 / 2. Mais cette fois nous allons utiliser des cubes au lieu de carrés. On applique alors le même principe d'alignement des N unités géométriques, mais cette fois cubiques, et donc dans un cube de dimension NxNxN, au lieu d'un carré NxN.

∑n=1N n2 est donc le nombre de petits cubes formant cet objet pyramidal. Pour déterminer ce nombre, constatons la symétrie de cette pyramide à l'intérieur du grand cube : le volume de celui-ci correspond au volume total de ces trois pyramides, de sorte que la réponse approximative à notre question est donc :
∑n=1N n2 ≈ N3 / 3

- ∑n=1N n ≈ N 2 / 2
- ∑n=1N n2 ≈ N 3 / 3
Il reste alors à substituer cette valeur dans :
VN = π * R2 * H / N3 * ∑n=1N n2
pour obtenir une approximation du volume du presque cône :
VN ≈ π * R2 * H / N3 * N3 / 3 ⇔
VN ≈ π * R2 * H / 3
Par conséquent le volume du cône est :
V = limN→∞ VN ⇒
V = π * R2 * H / 3
On notera que le volume du cône vaut le tiers du cylindre de même base et hauteur. Et l'on se rappellera que la surface du triangle vaut la moitié de celle du rectangle de même base et hauteur.
Ce faisant, Archimède a posé les bases conceptuelles du calcul intégral que Newton et Leibniz formaliseront algébriquement deux mille ans plus tard (17-18° siècle).

Trigonométrie
2. Angles dans le cercle
3. Sinus, cosinus, tangente
Somme des angles du triangle
La somme des angles d'un triangle quelconque vaut 180° ou π rad.
Pour le démontrer géométriquement, il suffit de translater le triangle (c-à-d le déplacer parallèlement à lui-même) pour placer sa copie de sorte que les angles a du triangle supérieur et c du triangle inférieur forment 180° avec l'angle qui les séparent (cf. graphique ci-joint). Or celui-ci est nécessairement le troisième angle b puisque le triangle a été déplacé parallèlement à lui-même.
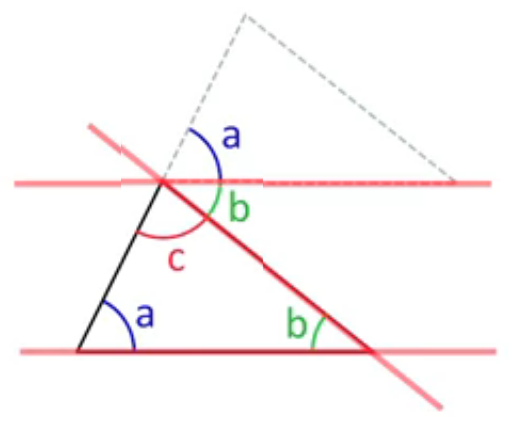
N.d.A. : autre démonstration. La somme des angles d'un rectangle vaut 4*90°=360° ⇒ la somme des angles de chacun des deux triangles dessinés par la diagonale représente 360°/2=180°. Or ce résultat est inchangé si l'on transforme ce rectangle en parallélogramme de même surface, et les deux triangles rectangles deviennent ainsi quelconques.
Angles dans le cercle
Nous allons voir ici deux théorèmes importants :
Le théorème de l’angle au centre dit qu' "un angle au centre d’un cercle (en rouge dans le schéma suivant) vaut le double de tout angle inscrit au cercle et interceptant le même arc de ce cercle" (en violet).

Les angles bleu et vert interceptent le même arc de cercle (en violet)) que l'angle au centre (en rouge).
Pour démontrer le théorème on va commencer par le cas particulier (cf. schéma suivant) où un des côtés de l'angle inscrit recouvre un des côtés de l'angle au centre, de sorte qu'il constitue ainsi un diamètre du cercle.
N.B. Dans ce cas, une des extrémités de l’arc intercepté par les deux angles (point E) se situe sur le même diamètre que le sommet de l’angle inscrit (point C).

N.d.A. Je propose ici un début de démonstration différent de celui de la vidéo. Sur la gauche apparaît alors un triangle isocèle – deux de ses côtés sont de grandeurs égales (au rayon du cercle) – de sorte que les deux angles déterminés avec eux par le troisième côté sont égaux (c) ⇒ puisque la somme des angles d'un triangle vaut 2π (30), alors le troisième angle vaut :
2π - 2 * c
or la somme de cet angle et de l'angle o vaut également 2π :
2π - 2 * c + o = 2π ⇔
o = 2 * c
On va pouvoir maintenant se baser sur ce résultat pour généraliser le théorème. Dans le schéma suivant on trace la droite hachurée passant par C et le centre du cercle, ce qui étend l'arc de cercle de D-E à D-F.

Ce faisant, on fait apparaître deux configurations (c1, o1) et (c2, o2) .... correspondent au cas que nous venons de démontrer ⇒
o1 = 2 * c1
o2 = 2 * c2
à quoi on peut ajouter que :
c = c1 + c2
o = o1 + o2
⇒ en substituant les deux premières égalités dans la quatrième, le système se réduit à deux équations :
c = c1 + c2
o = 2 * c1 + 2 * c2
⇔
o = 2 * c
CQFD
Ces principes valent évidemment également pour le cas où le diamètre se situe à l'intérieur des triangles : on tire toujours une droite de C vers O, etc.


Le théorème de l'angle au centre permet de montrer que l'oeil, en raison de sa forme sphérique, neutralise le grossissement des objets situés en bord du champ de vision, distorsion typique des appareils photographiques en raison de la forme planaire du film photographique.
Dans le schéma suivant, l'objet renvoie un faisceau jaune vers l'appareil, mais celui-ci est orienté de telle sorte que l'objet se trouve sur le bord droit du champ de vision de l'appareil. Il en résulte que l'image de l'objet sur le film photographique est élargie, car le film est incliné par rapport au faisceau lumineux reflété par l'objet.

Nous allons montrer, grâce au théorème de l'angle au centre, qu'en raison de la forme sphérique de l'oeil, l'image d'un objet au bord du champ de vision n'est pas déformée.
Le schéma suivant montre deux angles au centre (en rouge) :
celui du dessus, qui correspond à l'image de l'objet lorsqu'il se trouve près du bord droit du champ de vision de l'appareil (ce champ de vision étant centré autour de la flèche grise) ;
celui du dessous, qui correspond à l'image de l'objet s'il se trouvait au centre du champ de vision de l'appareil (c-à-d si la flèche grise, passant à travers le diaphragme, était horizontale).
Le théorème de l'angle au centre nous permet de démontrer que l'image correspondant à la situation du dessus est identique à l'image correspondant à celle du dessous, et donc non déformée, car les deux arcs de cercle sont de même longueur. En effet, ces deux arcs de cercle correspondent tous deux à un angle inscrit d'amplitude c, de sorte que, selon le théorème, ils correspondent tous deux un à un angle au centre d'amplitude o=2c, et ont donc la même longueur.

Le théorème de l'angle inscrit stipule que deux angles inscrits qui interceptent le même arc ont la même mesure.

La démonstration en est triviale puisqu'il s'agit d'un simple corollaire du théorème de l'angle au centre ↑ : deux angles inscrits qui interceptent le même arc valent tous deux le double de l'angle au centre (o) correspondant à cet arc, et ont par conséquent la même valeur o / 2.

En raison de son importance, les scientifiques ont élevé ce corollaire au statut de théorème, sans plus de référence au théorème de l'angle au centre.
Pour étudier les propriétés physico-chimiques du soleil, une méthode déductive consiste à analyser la lumière qu'il émet (spectroscopie). La lumière du soleil est composée de différentes couleurs correspondant chacune à une longueur d'onde lumineuse spécifique.
Les couleurs composant la lumière du soleil sont observables dans un arc-en-ciel : bleu, vert, jaune, rouge, etc. Le graphique suivant est une mesure du spectre du soleil. Il exprime l'intensité lumineuse en fonction de la longueur d'onde : des ultraviolets (courtes longueurs d'onde) aux infrarouges (grandes longueurs d'onde).
Spectre de la lumière solaire

Différentes techniques permettent de décomposer la lumière en ses composantes de couleurs. On peut observer ce phénomène sur un CD-ROM (cf. illustration ci-dessous). Sa surface est gravée de rayures concentriques très proches (de l'ordre du micron), ce qui a pour effet qu'un rayon lumineux qui vient la frapper est réfléchi selon un angle (noté θ) fonction de la longueur d'onde (notée λ). Ainsi la couleur bleue, ayant une longueur d'onde plus courte que le rouge, est réfléchie selon un angle plus petit. Ce système qui sépare les couleurs angulairement permet ainsi de décomposer la lumière.
Décomposition de la lumière

La lentille a pour effet de paralléliser les rayons divergents issus de la source lumineuse. La caméra représente un oeil observant le CD-ROM.
Mais dans la configuration ci-dessus, le spectre enregistré par la caméra est confus : les zones de couleurs ne sont pas parfaitement regroupées. Le schéma suivant montre que pour regrouper les couleurs, il faut éloigner la caméra du réseau de diffraction.


Si l'on éloigne encore la caméra jusqu'à ce que les zones d'interférences disparaissent complètement, on obtient alors le spectre suivant.

Mais nous allons voir que ce spectre mesuré par le système de spectrométrie ci-dessus n'est qu'une représentation grossière du spectre de la lumière solaire.

Pour nous en rendre compte, commençons par une source lumineuse plus simple que le soleil, composée de la superposition de trois rayons lasers de différentes longueurs d'onde : bleu, vert et rouge.

La particularité du laser est qu'il émet une longueur d'onde très précise. Un spectroscope précis devrait donc produire un spectre composé de trois lignes, correspondant chacune à la longueur d'onde spécifique de chaque laser.

Or nous avons vu que le système spectrométrique supra ne pourra produire qu'un spectre très grossier, composé de trois bandes de couleurs contiguës.
Une solution, proposée par Henry Rowland (1848-1901), consiste à remplacer le réseau de diffraction plan par un réseau courbé, ce qui va permettre d'exploiter la propriété de l'angle inscrit.
Plaçons une source laser (par exemple la bleue) sur le cercle, orientée vers un point du réseau de diffraction courbe. Le rayon bleu est diffracté selon l'angle λ correspondant à sa longueur d'onde. Sa projection détermine l'autre bout de l'arc de cercle correspondant à l'angle inscrit de grandeur λ et commençant à la source lumineuse. En vertu de théorème de l'angle inscrit, il en ira de même de tous les rayons bleus provenant de la source de lumière bleue, de sorte qu'ils convergeront tous vers l'autre bout de cet arc.

Il en va évidemment de même pour les deux autres couleurs issues du même point source, mais elles convergent chacune vers leur propre point correspondant à leur propre angle de diffraction, déterminé par leur longueur d'onde spécifique. La mesure de ces trois points de convergence correspond au spectre en bâtonnets représenté plus haut.

Ce système inventé par Rowland permet d'obtenir un spectre très fin de la lumière solaire (cf. les trous dans le spectre solaire, correspondant aux longueurs d'ondes de faible intensité). Ces données livrent des informations permettant de déduire des propriétés physico-chimiques du soleil.
Spectre de la lumière solaire

Sinus, cosinus, tangente
N.d.A. La première définition mathématique moderne du sinus aurait été donnée par l'astronome et mathématicien indien Aryabhata (476-550) [source].
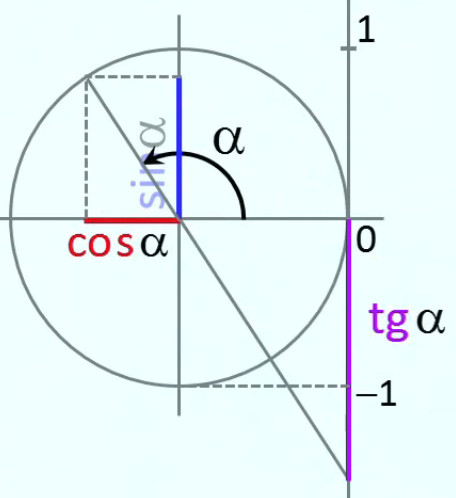
Par définition (⇒ ne se démontre pas), dans un triangle rectangle, le sinus d'un angle est le rapport entre son côté opposé et l'hypoténuse :
sin(a) ≡ y / R
⇔ y = R * sin(a) : y est la projection de R par sin(a) ... où a est l'angle opposé à y
⇔ R = y / sin(a) : R est la projection de y par 1/sin(a)
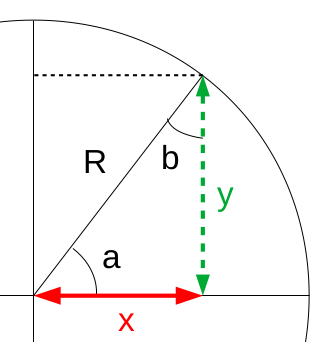
N.B. : si R = 1 ⇒ y = sin(a).
Par définition, dans un triangle rectangle, le cosinus d'un angle est le rapport entre son côté adjacent (c-à-d celui qui le relie à l'angle droit) et l'hypoténuse :
cos(a) ≡ x / R
⇔ x = R * cos(a) : x est la projection de R par cos(a) ... où a est l'angle adjacent à x
⇔ R = x / cos(a) : R est la projection de x par 1/cos(a)
N.B. : si R = 1 ⇒ x = cos(a).
Par (31) et (32) :
cos(a) = sin (b) ⇒
par (30) :
cos(a) = sin (90-a)
⇔
sin(a) = cos(90-a)
Loi de projection. On peut alors généraliser en disant que :
- tout côté adjacent de l'hypoténuse est la projection de celle-ci : soit par le cosinus de l'angle qu'il forme avec elle, soit par le sinus de l'angle opposé ;
- l'hypoténuse est la projection de chacun des autres côtés : soit par l'inverse du cosinus de l'angle qu'il forme avec lui , soit par l'inverse du sinus de l'angle opposé.
Loi des sinus : dans un triangle quelconque, le rapport entre le sinus d'un angle et son côté opposé est identique pour les trois angles ⇒
sin(α) / a = sin(β) / b = sin(γ) / c .
Démonstration par (34) :
H = c * sin(β) = b * sin(γ) ⇔
H = c / sin(γ) = b / sin(β) ⇒
même principe en prenant un autre côté commé référentiel ⇒ CQFD.
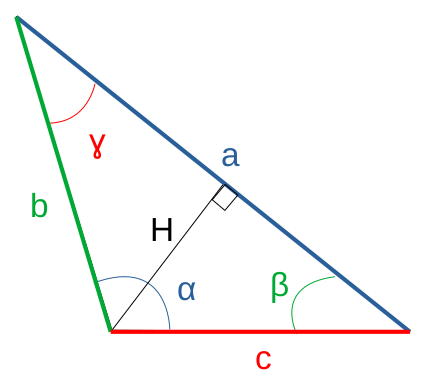
- c = a * sin(γ) / sin(α) où l'on a bien que si α=π/2 ⇒ c= a/sin(γ).
- c = b * sin(γ) / sin(β) où l'on a bien que si β=π/2 ⇒ c= b/sin(γ).
Par (31) et (32) substitués dans (23) :
sin2(a) + cos2(a) = 1
Addition : soient a et b deux angles quelconques dans le cercle trigonométrique de rayon 1 :
- sin(a+b) = sin(a) * cos(b) + cos(a) * sin(b)
- cos(a+b) = cos(a) * cos(b) - sin(a) * sin(b)
.png)
Pour démontrer sin(a+b) on détermine un référentiel pour l'angle b, obtenu par rotation du référentiel de a par la valeur de a. On va alors projeter sin(b) et cos(b) sur l'axe des sinus dans le référentiel de a :
(i) le segment rouge continu est la projection du rayon R=1 par cos(b) c-à-d cos(b) ; par (33) sa projection sur le segment rouge hachuré vaut sin(a) * cos(b) ;
(ii) le segment bleu continu est la projection du rayon R=1 par sin(b) c-à-d sin(b) ; sa projection sur le segment bleu hachuré vaut cos(a) * sin(b) (PS : c'est bien l'angle a que l'on retrouve là car ses côtés sont perpendiculaires à ceux de a originel).
Nous verrons plus loin dans le cours que l'on peut démontrer ces propriétés algébriquement, plus simplement, en faisant appel à la fonction exponentielle.
Un cas particulier de (42) est :
cos(2a) = cos2(a) - sin2(a)
or sin2(a) + cos2(a) = 1
(37) ⇒
cos(2a) = 2 * cos2(a) - 1
cos(2a) = 1- 2 * sin2(a)
Même principe pour démontrer cos(a+b), mais cette fois ci on va projeter sin(b) et cos(b) sur l'axe des cosinus dans le référentiel de a :
(i) le segment fléché en violet est la projection de R=1 par cos(a+b);
(ii) le segment fléché en rouge est la projection de cos(b) par cos(a);
(iii) le segment fléché en bleu est la projection de sin(b) par sin(a) (PS : c'est bien l'angle a que l'on retrouve là car ses côtés sont perpendiculaires à ceux de a originel);
(iv) or on voit que le segment violet vaut le rouge moins le bleu.
.png)
Et en remplaçant b par -b on trouve facilement que :
- sin(a-b) = sin(a) * cos(b) - cos(a) * sin(b)
- cos(a-b) = cos(a) * cos(b) + sin(a) * sin(b)
Pour résoudre de nombreux calculs il est utile de connaître le sin et cos des "angles clés" que sont 30° et 45°.
Si a=30° alors son symétrique par rapport à l'axe X forme avec a un angle de 60° ⇒ comme il y a symétrie chacun des deux autres angles vaut donc (180-60)/2=60° ⇒ le triangle est équilatéral ⇒ les trois côtés valent 1 ⇒
sin(30) = 1/2
⇒ par (37) : 1/4 + cos2(30) = 1 ⇒
cos(30) = √3 / 2
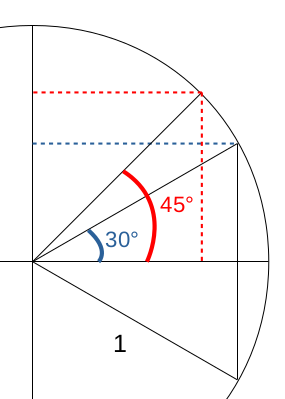
Si a=45° alors par symétrie sin(45)=cos(45) ⇒ par (37) :
sin(45) = cos(45) = 1 / √2
 Vidéos Clipedia :
La tangente : introduction // La fonction tangente // La circonférence de la Terre
Vidéos Clipedia :
La tangente : introduction // La fonction tangente // La circonférence de la Terre
Par définition, dans un triangle rectangle, la tangente d'un angle α (exprimé en radians) est le rapport entre sin(α) et cos(α) :
tan(α) ≡ sin(α) / cos(α)
ou encore entre ses côtés opposé (y) et adjacent (x) :
tan(α) = y / x :
• tan(α) est la pente de l'hypoténuse
• y = x * tan(α) : y est la projection de x par tan(α)
• x = y / tan(α) : x est la projection de y par 1/tan(α)
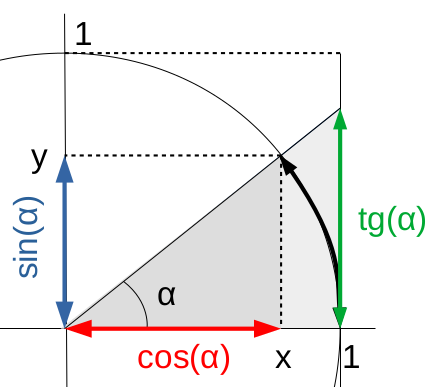
Propriétés visuelles remarquables :
• si α petit ⇒ sin(α) ≈ α et cos(α) ≈ 1 tg(α) ≈ α
⇔ la droite verte de longueur tg(α) et la courbe noire de longueur α se confondent (ainsi pour de petits angles la tangente vaut l'angle exprimé en radians).
À partir du graphique précédent, en augmentant progressivement l'angle α à partir de 0π radian , on peut construire le graphique suivant.
On visualise ainsi :
- le rythme imprimé par les segments de π/2 ;
l'explication algébrique du comportement asymptotique de la tangent, et de ses changements de signe, par l'égalité tg(α) = sin(α) / cos(α) ; NB : les sommets de la fonction tan() sont à l'infini, et correspondent à deux valeurs opposées (∞ et -∞ pour un même angle ...) ;
la période de la tangente (soit π), qui est la moitié de celle des sinus et cosinus ; tan(α) = tan(π-α) = - tan(α - π) NB : de par la seconde égalité la fonction tangente est dite "anti-symétrique" ; exemple : tan(225°) = tan(225°-180°) = tan(45°) = 1 .
Vecteur
2. Addition et multiplication
3. Produit scalaire
4. Produit vectoriel
Définition
 Vidéos Clipedia : Les vecteurs : introduction // La norme d'un vecteur // Les vecteurs à deux dimensions : introduction
Vidéos Clipedia : Les vecteurs : introduction // La norme d'un vecteur // Les vecteurs à deux dimensions : introduction
Un vecteur est entièrement déterminé par deux points de l'espace, l'un étant considéré comme l'origine du vecteur. Ainsi à eux deux ils déterminent :
- une direction, déterminée par la droite passant par ces deux points ;
N.d.A. Deux vecteurs ont même direction s'ils sont parallèles ⇔ aller dans la même direction ne signifie pas converger vers le même point (bien que deux droites parallèles, dans un espace de dimension 2, sont supposées converger ... à l'infini).
- un sens, allant du point origine vers le point extrémité (généralement représenté par une flèche) ;
- une grandeur (longueur, vitesse, force, ...) – encore appelée "norme" ou "module" – déterminée par la distance entre origine et extrémité du vecteur.
Le rayon d'une sphère correspond à cette triple définition, et est donc un vecteur.
Référentiel. Le schéma suivant illustre que – dès lors qu'à tout vecteur correspond un espace à une dimension (c-à-d une droite) qui le contient – il suffit alors de normer cet axe en y déterminant un point "zéro" et un point "unité", pour calculer la valeur de tout vecteur sur cette axe normé, comme étant la différence entre la coordonnée de son extrémité et celle de son origine.
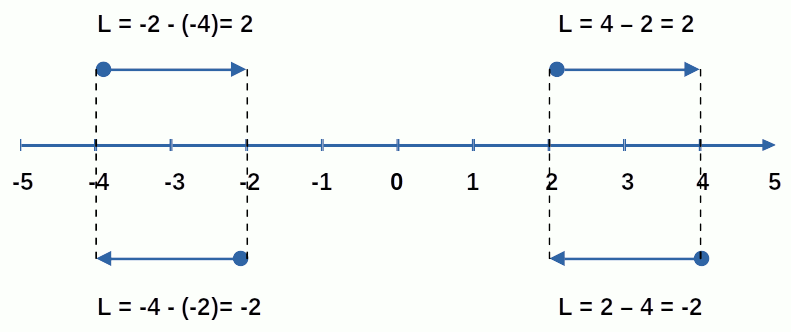
N.B. Les vecteurs de valeur négative sont orientés dans le sens opposé à celui de l'axe normé.
valeur = module≡longueur * signe≡sens :
- la longueur du vecteur (notion géométrique), c-à-d sa valeur absolue (notion algébrique), est appelée "module" ;
- le sens vecteur (notion géométrique) correspond à son signe (notion algébrique).
| Géométrie | Algèbre |
|---|---|
| Longueur | VA |
| Sens | Signe +/- |
Composantes Algébriquement, dans un espace de dimension n, un vecteur peut être formulé par un n-uplet de cordonnées cartésiennes. Ainsi dans l'espace de dimension 2 :
a→ = (ax, ay) (cf. schéma infra).
N.d.A. Soulignons que (50) est une égalité de notations : a→ est la notation géométrique, tandis que (ax, ay) est la notation algébrique.
Le schéma suivant montre deux positions du même vecteur a→ = (ax, ay) (ou encore, de deux vecteurs de même module, direction et sens). Ainsi un vecteur peut être situé aussi bien à l'origine du repère cartésien que, par translation, n'importe ou ailleurs dans ce repère. Au niveau terminologique, on distingue :
- "vecteur déplacement" (cf. partie gauche du schéma suivant) ⇔ ax et ay sont appelées composantes du vecteur : pour exprimer un déplacement entre l'origine et l'extrémité du vecteur ;
- "vecteur position" (cf. partie droite du schéma) ⇔ ax et ay sont appelées coordonnées du vecteur : pour exprimer la position du point déterminé par l'extrémité du vecteur, lorsque celui-ci est positionné à l'origine (0,0) du repère cartésien.
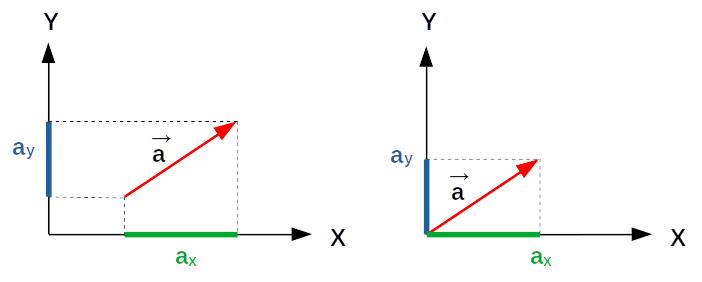
N.d.A. La notion de vecteur implique celles de référentiel (le repère cartésien) et de relativité par rapport à différents référentiels (cf. /dynamique#relativite).
Le vecteur ci-dessus, qui est inscrit dans le plan (X,Y), sera noté dans l'espace de dimension 3 (X,Y,Z) : a→ = (ax, ay, 0) où az=0.
Calcul. Le schéma précédent révèle que le module de a→, noté || a→|| , peut être calculé par le théorème de Pythagore ("le carré de l'hypoténuse vaut la somme des carrés des deux autres côtés") (23) :
|| a→|| = √(ax2 + ay2)
Par convention on écrit souvent simplement a au lieu de || a→|| .
On parle de module en cas de grandeur physique (avec une unité spécifique – par exemple le Newton (N) dans le cas de la force F = m * a [kg * m / s2 = N] (168) – et de norme dans le cas d'une grandeur grandeur mathématique sans dimension (c-à-d sans unité).
Addition et multiplication
Addition. Les coordonnés cartésiennes permettent de calculer les coordonnées d'une somme de deux vecteurs en additionnant leurs composantes homologues : a→ + b→ = (ax , ay) + (bx , by) = ( ax + bx , ay + by )
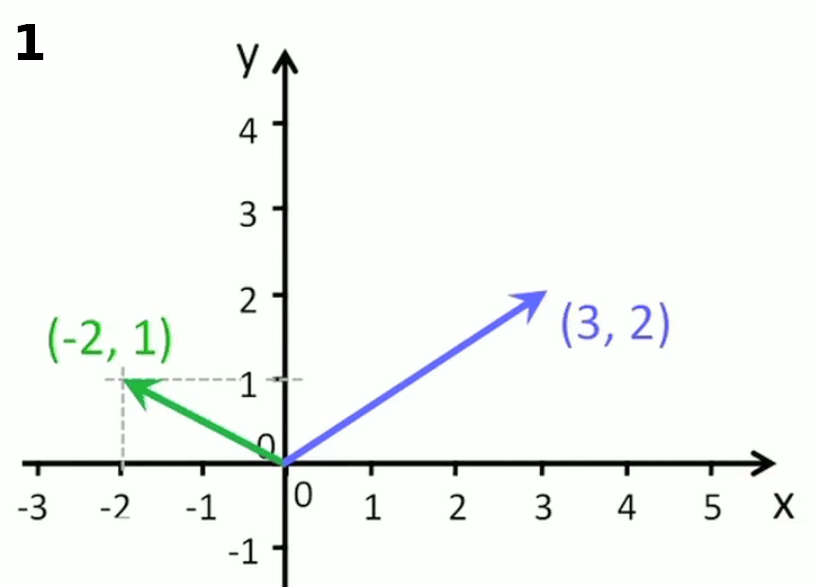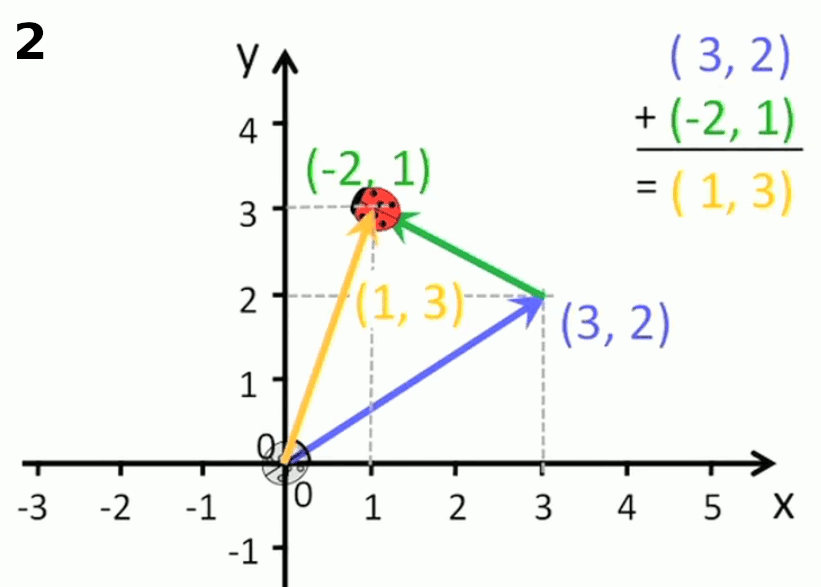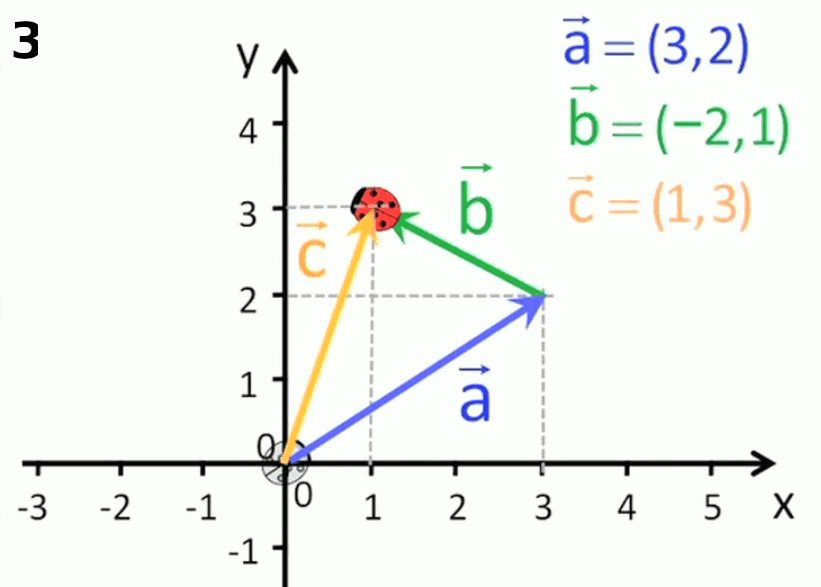
Ainsi dans l'animation suivante, le vecteur (-2,1) est translaté de l'origine du repère cartésien jusqu'à l'extrémité du vecteur (3,2). On constate alors que le vecteur allant de l'origine du premier vecteur à l'extrémité du second enchaîné a pour composantes l'addition des composantes homologies des deux vecteurs enchaînés.
Multiplication. Il en découle logiquement que la multiplication vectorielle, c-à-d le produit d'un vecteur par lui-même, se fait par multiplication des composantes par le facteur de multiplication : n * a→ = ( n * ax , n * ay )
Il suffit alors de poser n=-1 pour définir le vecteur opposé, et la soustraction vectorielle à partir de (52).
Géométriquement (graphique suivant) :
- a→ + b→ est le vecteur allant de l'origine de a→ à l'extrémité de b→ lorsque celui-ci est positionné à l'extrémité de a→.
- a→ - b→ est le vecteur allant de l'extrémité de b→ à celle de a→ lorsque les deux vecteurs sont positionnés à la même origine.
Ainsi l'on pourra vérifier dans le graphique ci-dessous que b→ + (a→ - b→) = a→

- on dessine - b→, comme l'opposé de b→ à partir de son origine (non-dessiné ci-dessus);
- on translate - b→ à la suite de a→;
- apparaît a→-b→, de l'origine de a→ vers l'extrémité de la translation de - b→;
- on translante a→-b→ sur l'extrémité de b→ ⇒ on constate que l'extrémite de a→-b→ correspond à celle de a→, c-à-d que b→ + (a→ - b→) = a→. C'est la règle (55) énoncée ci-dessus.
Vecteur unitaire (N.d.A.)
Le vecteur unitaire est indispensable à la mesure du vecteur. Il permet ainsi de passer de la formulation géométrique à la formulation algébrique du vecteur. Le graphique suivant montre que :
1→ = 1x→ + 1x→ ⇔
1→ = (1x,0) + (0,1y) ⇔
1→ = (1x,1y)
En posant que 1→ = (1x,1y) plutôt que le cas particulier 1→ = (1,1), on a la possibilité de poser 1y = k * 1x, ce qui permet par exemple d'écraser ou étirer une image vectorielle en jouant sur la valeur de k.
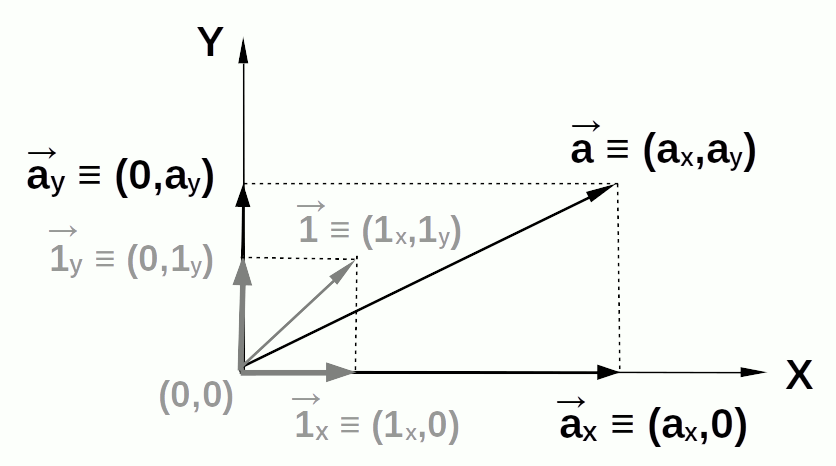
Exprimer un vecteur quelconque en fonction du vecteur unitaire :
par définition de l'addition vectorielle :
a→ = ax→ + ay→ ⇔
a→ = (ax,0) + (0,ay) ⇔
par définition de la multiplication vectorielle :
a→ = ax * (1x,0) + ay * (0,1y) ⇔
a→ = ax * 1x→ + ay * 1y→
D'autre part :
(ax,0) = ax * (1x,0) ⇔
ax→ = ax * 1x→ ⇔
1x→ = ax→ / ||ax→||
⇔
plus généralement :
« le vecteur unité est le rapport entre un vecteur de même direction et la norme de ce vecteur ».
Quant à la relation entre le vecteur unité 1→ et un vecteur quelconque a→, le graphique supra montre trivialement que a→ = 1→ + ( a→ - 1→ )
Le lecteur trouvera une application très explicite de la notion de vecteur unitaire dans le chapitre consacré au passage de la forme scalaire de la loi de Coulomb à sa forme vectorielle : cf. infra #loi-coulomb.
Produit scalaire
Supposons une boule déposée sur une pente, puis laissée à elle-même. Elle va alors descendre le long de la pente (d'angle θ mesuré par rapport à la verticale), sous l'effet de la force f→. Le schéma infra montre que cette force est résultante de deux autres, selon la définition de l'addition vectorielle (54), c-à-d en l'occurrence, telle que f→ = F→ + (- A→) où :
F→ : attraction terrestre (dite force de gravitation) :
- module constant ;
- verticale et orientée vers le bas.
A→ : résistance exercée par le sol contre le poids de la boule :
- module variable en fonction de l'angle θ ;
- perpendiculaire au sol et orientée vers le haut.
f→ : force résultante (pour un angle θ donné) :
- module variable en fonction de l'angle θ ;
- parallèle à la pente et orientée vers le bas (dès lors que 0° < θ < 90°). Autrement dit, pour pousser la boule vers le haut, il faut contrer f→ (orientée vers le bas) par f→ (orientée vers le haut).
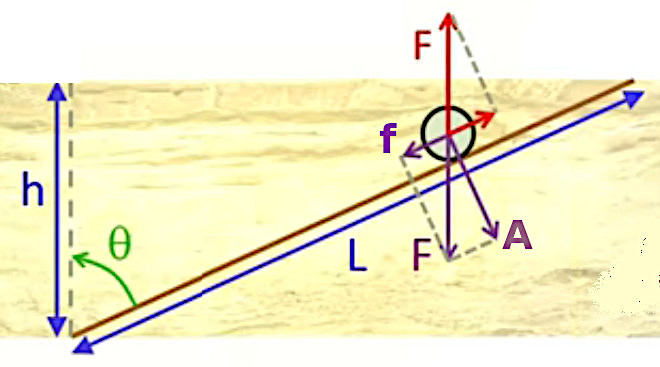
N.B. Ce sont les modules qui sont ici représentés. Ainsi la flèche A correspond bien au module de - A→.
Ainsi, lorsque la pente passe de l'horizontale (A = F et f = 0) à la verticale (A = 0 et f→ = F→) ⇒ A diminue de F à zéro, tandis que f augmente de zéro à F. La pente telle que 0° < θ < 90° agit donc comme un outil qui permet d'élever la boule avec une force f < F mais sur une distance d'autant plus longue que θ est élevé c-à-d que la pente est faible (« on a rien sans rien » : nous y reviendrons dans un instant...).
D'autre part, le schéma ci-dessus montre deux projections concomitantes :
- la hauteur h est la projection de la longueur L par le cosinus de l'angle (θ)) qu'elles forment ⇔ h = L * cos(θ) par (32).
- f est la projection de F sur la pente (c-à-d dans la direction déterminé par A), de sorte que l'angle formé par f et F→ est ce même angle θ ⇒ f = F * cos(θ) .
Enfin, le principe de conservation de l'énergie nous dit que le travail W = force * distance (173) fourni pour élever la boule d'une hauteur h en la poussant le long d'une pente d'inclinaison θ quelconque (ou longueur L correspondante selon h = L * cos(θ) (32)) est identique à la force nécessaire pour élever la boule verticalement à cette même hauteur h :
W(L) = W(h) ⇔
f * L = F * h ⇒ en remplaçant :
- dans le membre de gauche, f par sa son expression en projection
- dans le membre de droite, h par son expression en projection.
⇒
F * cos(θ) * L = F * cos(θ) * L
N.B. L'égalité qui conclut le développement ci-dessus démontre donc le prémisse de ce développement, à savoir la loi de conservation de l'énergie !
L'égalité ci-dessus montre donc que le travail W peut être interprété de deux façons :
- membre de gauche : L fois la projection de la force F via l'angle θ sur le sens du déplacement L ;
- membre de droite : F fois la projection du déplacement L via l'angle θ sur la direction de F.
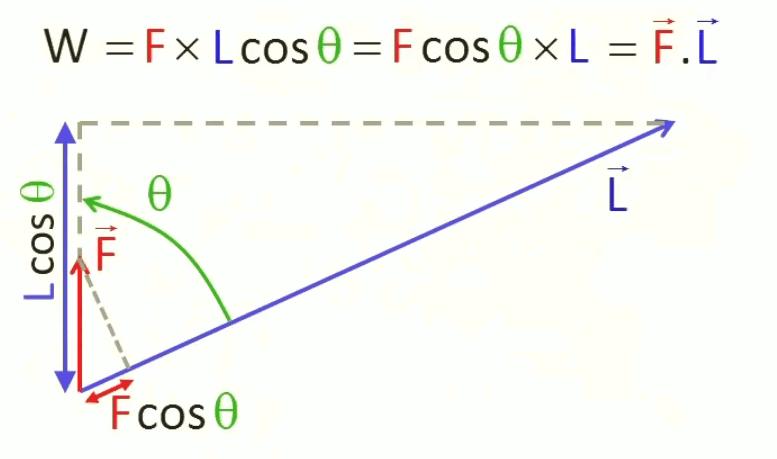
Interprétation spécifique : la notion de produit scalaire permet ici de comparer deux interprétations du même travail : effectué verticalement vs le long de la pente d'angle θ (calculé relativement à la verticale).
Cette situation de symétrie est souvent observée dans les phénomènes physiques. Et pour la noter de façon compacte, on va utiliser une notion appelée "produit scalaire" de F→ (vecteur "force") et L→ (vecteur "déplacement") :
F→ . L→ = || F→|| * || L→|| * cos θ
c-à-d :
« le produit des modules des deux vecteurs, multiplié par le cosinus de l'angle que forment ces vecteurs ».
ou encore :
« le produit du module d'un vecteur par la projection sur lui du module de l'autre vecteur ».
Interprétation générale. Le produit scalaire permet donc de multiplier le module de deux vecteurs, dont l'un est sa projection sur l'autre.
N.B. Il ressort du membre de droite de (58) que le produit des deux vecteurs du membre de gauche n'est pas un vecteur mais un nombre ! C'est pourquoi ce produit est dit "scalaire".
La formulation algébrique du produit scalaire – c-à-d en fonction de ses composantes cartésiennes plutôt que angulaires – repose sur le fait que les vecteurs "force" et "déplacement" sont caractérisés par leurs angles spécifiques, dont l'angle θ est la différence (cf. schéma ci-dessous, représentant les deux vecteurs dans un repère cartésien).
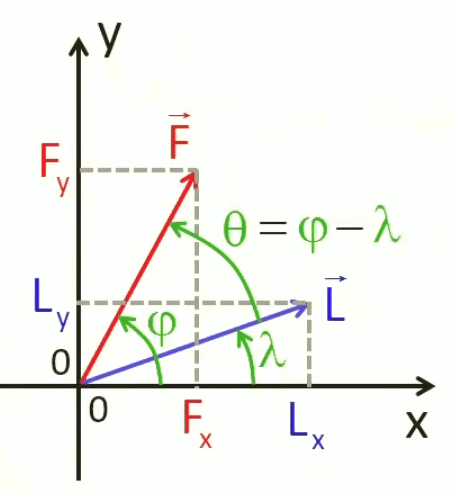
Les vecteurs F→ et L→ sont représentés dans ce repère cartésien en fonction de leur composantes en X et Y : (Fx, Fy) et (Lx, Ly).
La formulation algébrique du produit scalaire de F→ et L→ se déduit de la formulation trigonométrique :
F→ . L→ = F * L * cos θ (58) ⇔
F→ . L→ = F * L * cos ( φ - λ ) ⇒ par (42) :
F→ . L→ = F * L * ( cos φ * cos λ + sin φ * sin λ ) ⇔
F→ . L→ = F * cos φ * L * cos λ + F * sin φ * L * sin λ ⇒
par (31) et par (32) :
F→ . L→ ≡ (Fx, Fy) . (Lx, Ly) = Fx * Lx + Fy * Ly
: « le produit scalaire est donné par la somme des produits des composantes homologues » (PS : il est donc bien un nombre, d'où le qualificateur de scalaire ("échelle" en latin) car ce nombre correspond à une position sur cette échelle normée qu'est la droite des réels).
Illustrons le cas de Fx dans le graphique supra : il s'agit bien de la projection de F→ par l'angle φ.
En résumé, le graphique suivant représente les deux formulations du produit scalaire :
- cartésienne (algébrique) : « somme des produits des composantes homologues » ;
- trigonométrique (géométrique) :
- « produit des modules des deux vecteurs, multiplié par le cosinus de l'angle que forment ces vecteurs » ;
- « produit du module d'un vecteur par la projection sur lui du module de l'autre vecteur ».
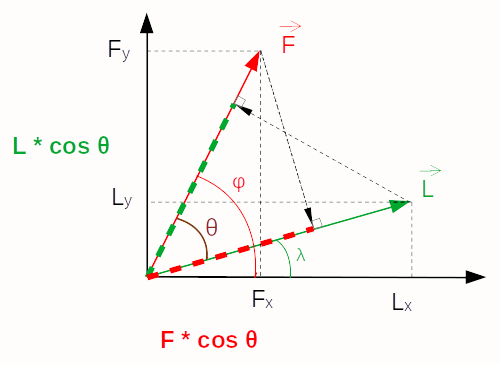
Formulation trigonométrique (géométrique) : F * cos(θ) * L = L * cos(θ) * F. Les deux membres sont bien égaux, et sont plus simplement notés F→ . L→
Commutatif :
a→ . b→ = a * b * cos(θ) = b * a * cos(-θ) = b→ . a→
CQFD
La démonstration est encore plus triviale à partir de la formulation algébrique du produit scalaire (59).
Distributif :
par (50) :
a→ . ( b→ + c→ )
= (ax,ay) . [ (bx,by) + (cx,cy) ] ⇔ par (52) :
a→ . ( b→ + c→ )
= (ax,ay) . ( (bx + cx ) , ( by + cy ) ) ⇔ par (59) :
a→ . ( b→ + c→ )
= ax * (bx + cx) + ay * (by + cy) ⇔
a→ . ( b→ + c→ )
= ax * bx + ax * cx + ay * by + ay * cy ⇔
a→ . ( b→ + c→ )
= ( ax * bx + ay * by ) + ( ax * cx + ay * cy ) ⇔ par (59) :
a→ . ( b→ + c→ )
= a→ . b→ + a→ . c→
CQFD
Non associatif :
a→ . b→ . c→ ≠ ( a→ . b→ ) . c→ ≠ a→ . ( b→ . c→ )
car le produit scalaire de trois vecteurs ne fait pas sens puisque (i) le produit scalaire est un nombre, (ii) il se fait entre deux vecteurs ⇒
a→ . b→ . c→ ≠ ( a→ . b→ ) * c→ ≠ a→ * ( b→ . c→ )
D'autre part, la seconde égalité est une évidence : m * c→ ≠ n * a→
N.d.A. Le fait que le produit scalaire ne fasse sens que pour un nombre pair de vecteur est lié à la nature symétrique du produit scalaire, géométriquement fondé sur deux projections-concomitantes.
Notons enfin quelques valeurs ou propriétés remarquables :
- a→ . a→ = a * a * cos(0) = ||a→||2
or par la forme algébrique du produit scalaire (59) :
a→ . a→ = ... = ax2 + ay2 ⇒
||a→|| = √(ax2 + ay2)
Nous venons donc de démontrer le théorème de Pythagore. Le produit scalaire de deux vecteurs perpendiculaires vaut zéro, puisque cosθ=0 si θ=π/2 : ( a→ . b→ )⊥ = a * b * cos(0) = 0
- Si θ>π/2 ⇒ cos(θ)<0 ⇒ a→.b→<0 : lorsque la projection de ||b→|| sur ||a→|| se fait dans la direction opposée de a→ le produit scalaire est alors négatif !
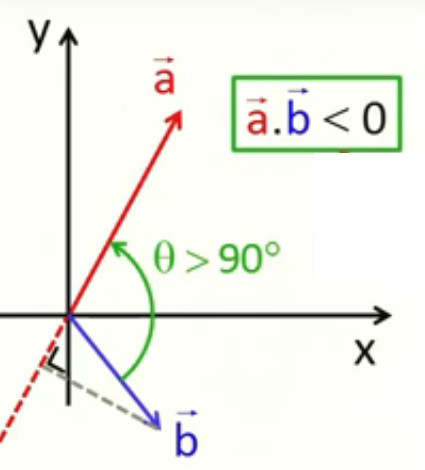
- On ne peut diviser par un vecteur. Autrement dit, il n'existe pas d'opération / b→ qui serait l'inverse de . b→ :
- division d'un vecteur par un vecteur, telle que :
- a→ / b→ = c→ ⇔
a→ = c→ . b→
ce qui ne fait pas sens puisque le membre de gauche est un vecteur alors que celui de droite est un scalaire. - a→ / b→ = c ⇔
a→ = c . b→
or un produit scalaire (.) multiplie un vecteur par un autre, et non un vecteur par un nombre ; en outre, même en écrivant :
a→ = c * b→
cela ne ferait pas plus sens puisque cette égalité signifie que a→ et b→ sont parallèles alors que dans l'égalité avec la division cela n'est pas le cas en toute généralité.
- a→ / b→ = c→ ⇔
- division d'un scalaire par un vecteur : a / b→ :
ne fait pas sens puisque, par définition de la division, cela signifierait qu'un vecteur rentrerait un certain nombre de fois dans un scalaire !
- division d'un vecteur par un vecteur, telle que :
Produit vectoriel
2. Calcul
3. Interprétation géométrique
Définition et propriétés
En introduction illustrative du produit vectoriel, nous évoquons la notion de moment de force, qui n'est étudiée que plus loin dans la présente publication, car elle repose sur les concepts de force et de levier (cf. /dynamique#rotation).
Soit un levier (en l'occurrence une clé) par rapport auquel est défini le moment de force (qui est un moment de torsion) τ = r * F * sin(θ) (178) où r est la longueur du bras de levier, et F la force exercée sur ce bras. Le moment de force exprime tout simplement la proportionnalité entre la force F*sin(θ) et la longueur du levier : en doublant celle-ci, on peut diminuer de moitié la force exercée sur lui (pour arriver au même résultat).
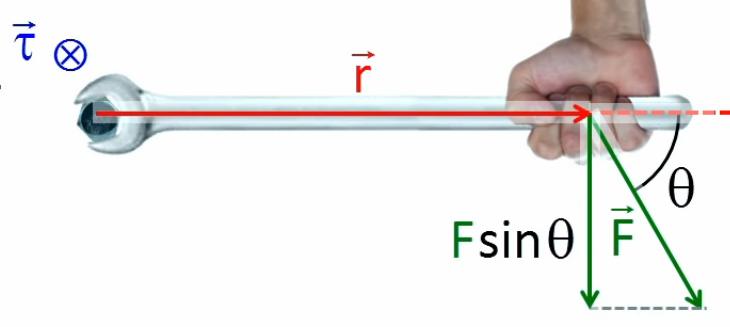
La composante longitudinale n'intervient pas dans la force de torsion → c'est F*sin(θ) que le moment τ rapporte à r.
Dans l'image ci-dessus la clé est utilisée par une personne quelque peu maladroite, qui exerce sa force dans la direction F→ plutôt que dans celle de la perpendiculaire à r→
Ce modèle mathématique qui quantifie l'intensité (le "module" infra) de l'effort de torsion ne dit cependant rien sur le sens de rotation qui est induit par cet effort (en l'occurrence on ne sait pas si on serre ou déserre). L'illustration géométrique ci-dessus donne certes la réponse, mais il reste à la formuler mathématiquement. Pour ce faire, le modèle a été complété par un outil mathématique appelé "produit vectoriel", consistant à représenter τ, r et F par des vecteurs : τ→ = r→ x F→ (179).
Notez le remplacement du signe * par le signe x, selon que le momeent de force est exprimé en tant que module τ = r * F * sin(θ) (178) ou en tant que vecteur τ→ = r→ x F→ (179).
Ainsi dans le graphique ci-dessus :
l'origine du vecteur "bras de levier" r→ représente le centre de rotation de la force, tandis que son extrémité représente le point d'application de cette force ;
- la direction du vecteur "force" F→ est donnée par l'angle θ.
NB : étant maintenant représentées sous forme de vecteurs, les grandeurs r→ et F→ ne doivent plus nécessairement être dessinées à la suite l'une de l'autre, mais peuvent aussi bien être ramenées à une origine commune.
On va ainsi généraliser sous forme vectorielle, en considérant des vecteurs quelconques (a→ et b→) à origine commune :
c→ = a→ x b→ = || a→|| * || b→|| * sin(θ) * 1→⊥
Le produit vectoriel se lit « a croix b ».
où :
• 1→, qui est un vecteur de longueur unitaire, convertit le nombre || a→|| * || b→|| * sin(θ) en vecteur;
• ⊥ indique que le produit vectoriel c→ est perpendiculaire au plan constitué par ses composantes a→ et b→, et que le signe (le sens) de 1→ est déterminé par la règle de la main droite.
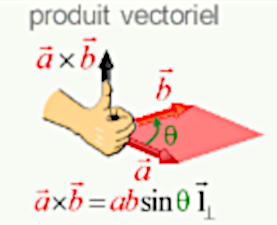
La formule trigonométrique du produit vectoriel (62) stipule que le vecteur c→ est perpendiculaire au plan déterminé par les vecteurs a→ et b→, dont il constitue le produit vectoriel. Cependant (62) ne dit rien sur le sens de cette direction. Pour cela, on a inventé la règle de la main droite.
Règle de la
main droite
La règle de la main droite est une convention qui permet de déterminer le sens du produit vectoriel c→ (soit le moment de force τ→ de notre exemple) : « quand le pouce de la main droite va dans le sens du vecteur c→, alors le sens dans lequel se plient les autres doigts indique le sens de rotation dans lequel l'angle θ est mesuré (l'autre sens correspondant à 2π-θ), ou encore le sens de rotation de l'axe déterminé par c→ ». Pratiquement : « soit le produit scalaire a→ x b→ = c→, replier la main droite sur l'angle formé par a→ et b→, à partir de a→, et dans le sens le plus court ⇒ le pouce indique le sens de c→ » (cf. schéma supra).
Ainsi dans le premier graphique illustrant le moment de force on appuie vers le bas et on visse (ce qui est indiqué par le signe "plume de flèche" ⊗, la direction opposée étant indiquée par signe "pointe de flèche" ⊙).C'est donc au travers du vecteur unitaire 1→⊥, et surtout de son signe, que la règle de la main droite est exprimée dans la formule du produit vectoriel.
Produit scalaire vs produit vectoriel
- Produit scalaire : a→ . b→ = || a→|| * || b→|| * cos(θ)
- Produit vectoriel : a→ x b→ = || a→|| * || b→|| * sin(θ) * 1→⊥
Le produit scalaire est un scalaire (nombre), tandis que le produit vectoriel est un vecteur.
Le produit scalaire projette le premier vecteur du produit perpendiculairement au deuxième vecteur (⇒ projection parallèle), tandis que le produit vectoriel projette le premier vecteur parallèlement au second (⇒ projection perpendiculaire).
https://clipedia-txt.net/geometrie#produit-scalaire-vs-vectoriel
Application
Force de Lorentz. Un exemple d'application du produit vectoriel est la force de Lorentz, c-à-d la force dite "magnétique" subie par une particule chargée dans un champ électromagnétique. Quand une charge électrique q se déplace à une vitesse v→ dans le champ magnétique B→ d'un aimant, elle subit une force :
f→ = q * v→ x B→
Le schéma suivant représente deux déplacements v→ de la charge q : celui de gauche est perpendiculaire au champ magnétique B→, tandis que le second lui est parallèle. La règle de la main droite permet alors de déterminer que dans le premier cas la force résultante (64) est dirigée vers le bas, tandis que dans le second elle est nulle (car l'angle θ est alors nul ⇒ son sinus également ⇒ le produit vectoriel q * v→ x B→ = q * v * B * sinθ * 1→⊥ également).
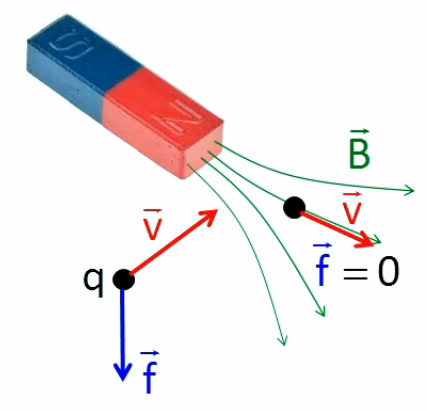
On constate ici toute la puissance du produit vectoriel, permettant de décrire par un simple produit vectoriel, un phénomène aussi complexe que celui décrit ici.
Reprenons maintenant le cas de la charge de gauche ci-dessus (direction perpendiculaire à celle du champ) mais d'un nouveau point de vue : cette fois en nous plaçant face au champ magnétique (NB : la "pointe de flèche" verte montre que le champ magnétique "sort de l'écran" dans notre direction). Exercez-vous à retrouver, grâce à la règle de la main droite, la direction de la force f→.
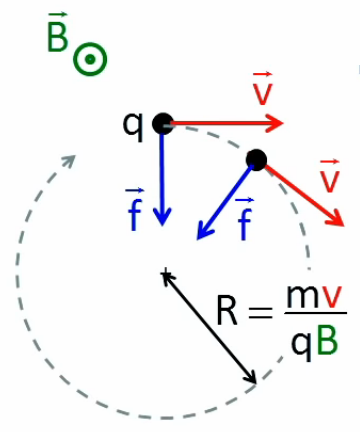
Le module de la force magnétique est f = q * v * B * sinθ où θ est l'angle entre la vitesse de la charge et le champ magnétique. Or comme on à posé θ=π/2 ⇒ sinθ=1 ⇒ f = q * v * B : la force exercée sur la charge est proportionnelle à la charge, sa vitesse, et à l'intensité du champ.
La force magnétique infléchit vers le bas la trajectoire composite de la charge, de sorte que cette trajectoire est courbée (la vitesse est donc inclinée vers le bas puisque la vitesse est toujours tangente à la trajectoire). Et comme, par définition du produit scalaire f→ = q * v→ x B→ = q * v * B * sinθ * 1→⊥ (62), la force magnétique f→ est perpendiculaire à la vitesse ⇒ ( v→ x B→ ) . v→ = 0 par (61) ⇒ le produit scalaire f→ . v→ = q * ( v→ x B→ ) . v→ = 0. Or on peut démontrer (en faisant référence à la mécanique avancée) que f→ * v→ traduit l'énergie fournie à la charge. Le champ électrique n'induit donc pas d'énergie cinétique ⇒ la vitesse de la particule est constante (en module). Or comme q et B sont donnés ⇒ f = q * v * B est également constante ⇒ la trajectoire est infléchie de façon constante ⇒ la courbure est constante ⇒ la trajectoire de la charge forme un cercle. Si on introduit alors la notion de force centrifuge qui équilibre la force centripète f (cf. (169) ), on peut alors montrer que le rayon de ce cercle (rayon de courbure) vaut R = m * v / ( q * B ) où m représente la masse de la particule. C'est grâce à la mesure de cette courbure que l'on peut identifier des particules élémentaires étudiées dans des laboratoires tels que le CERN. Si la particule est ralentie dans le détecteur ⇒ v ↓ ⇒ R ↓ ⇒ ce sont alors des spirales qui apparaissent jusqu'à former un point associé à la particule.
Rappelons que, dans le calcul du produit vectoriel a→ x b→ = || a→|| * || b→|| * sin(θ) * 1→⊥ (62), la règle de la main droite – symbolisé par l'indice ⊥ du vecteur unitaire – lève l'ambiguïté concernant le sens (horaire vs anti-horaire) dans lequel l'angle θ est considéré. En effet, la règle de la main droite stipule clairement que l'angle θ est calculé – et la règle de la main droit est appliquée – « de a→ vers b→ et dans le sens le plus court » (autrement dit : l'angle entre deux vecteurs ne peut dépasser 180° !).
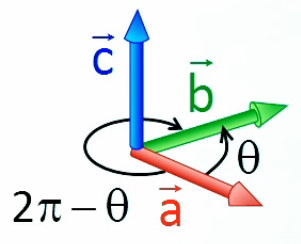
Les deux sens ne sont pas équivalents en terme de sinus : sin(θ) = - sin(2π-θ) ⇒
a→ x b→ = || a→|| * || b→|| * sin(θ) * 1→⊥ ⇔
a→ x b→ = - || a→|| * || b→|| * sin(2π-θ) * 1→⊥

Ce rappel étant fait, passons maintenant au propriétés du produit vectoriel.
Non commutatif.
a→ x b→ ≠ b→ x a→ ⇔
|| a→|| * || b→|| * sin(θ) * 1→⊥ ≠
|| b→|| * || a→|| * sin(-θ) * 1→⊥ ⇔
|| a→|| * || b→|| * sin(θ) * 1→⊥ ≠ -
|| a→|| * || b→|| * sin(θ) * 1→⊥
CQFD
PS : on dit également "anti-commutatif", ou encore "anti-symétrique" en raison du fait que seul le signe change :
soit c→ = a→ x b→ ⇒ b→ x a→ = - c→
Valeur remarquable : a→ x a→ = 0→ par (62) où θ=0.
Non associatif. Il résulte de (67) que :
a→ x ( a→ x b→ ) ≠ ( a→ x a→ ) x b→ = 0→
⇒ il existe au moins un cas où a→ x ( b→ x c→ ) ≠ ( a→ x b→ ) x b→ ⇔ on ne peut conclure que le produit vectoriel est associatif.
Distributif. La démonstration de la distributivité du produit vectoriel dans un espace 3D étant trop complexe on va se limiter ici à la démonstration dans un espace 2D :
a→ x ( b1→ + b2→ ) = a→ x b1→ + a→ x b2→ ⇔
a * ||b1→ + b2→ || * sinθ * 1→⊥ = a * b1 * sinθ1 * 1→⊥ + a * b2 * sinθ2 * 1→⊥ ⇔
||b1→ + b2→ || * sinθ * 1→⊥ = b1 * sinθ1 * 1→⊥ + b2 * sinθ2 * 1→⊥
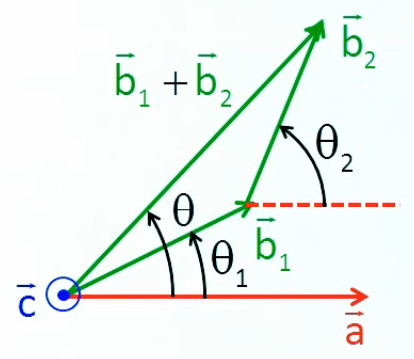
Malheureusement θ ≠ θ1 + θ2 puisque θ augmente si par exemple la norme de b1→ ou b2→ augmente.
On pourra néanmoins vérifier l'égalité supra en projetant ( b1→ + b2→ ), b1→ et b2→ sur la même perpendiculaire à a→, et en constatant qu'elles confirment l'égalité supra.
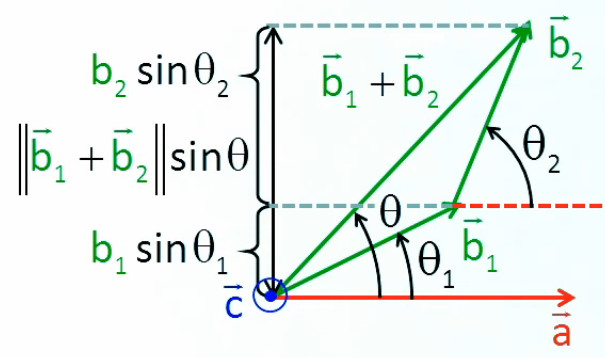
Calcul
À la fin de la vidéo précédente "Le produit vectoriel, propriétés", il est montré, à partir d'un exemple, que le calcul trigonométrique du produit scalaire (c-à-d à partir de a→ x b→ = || a→|| * || b→|| * sin(θ) * 1→⊥ (62)) est laborieux. Nous allons voir que son calcul algébrique est plus simple, grâce aux propriétés du produit scalaire exposées supra.
En exploitant les propriétés de distributivité et (67), on va développer une règle de calcul du produit vectoriel. N.B. : une condition est que le repère cartésien soit orthonormé (axes perpendiculaires) et dextrogyre (sens des axes déterminé par la règle de la main droite (63) ).
Si ces deux conditions sont respectées, on a alors que :
1→z = 1→x x 1→y
1→x = 1→y x 1→z
1→y = 1→z x 1→x
La lectrice pourra vérifier la cohérence des trois égalités ci-dessus (N.B. : qui ne contiennent aucun signe négatif) et l'application de la règle de la main droite à ces trois produits vectoriels unitaires représentés dans le schéma suivant.
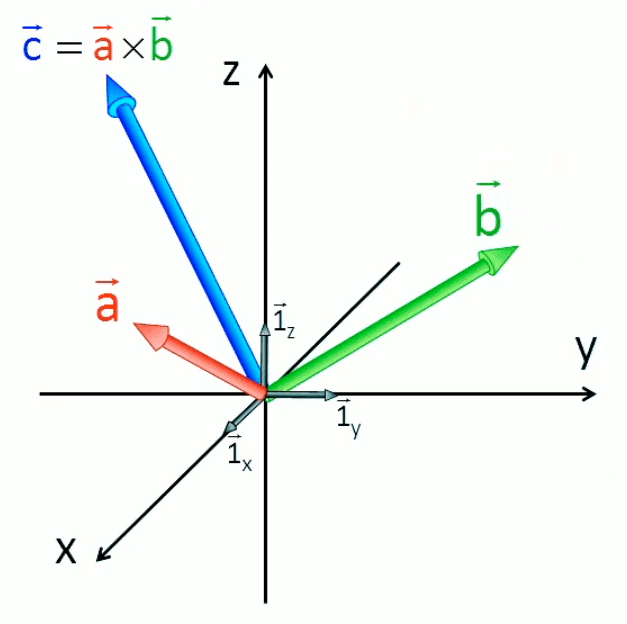
Il faut un peut d'exercice pour appliquer – à partir d'une image (donc en 2D), mais pour un produit vectoriel en 3D – la règle de la main droite « replier les doigts de la main droite, de a→ vers b→, et dans le sens le plus court ». Il faut se représenter le fait que le repliement se fait le long du plan formé par a→ et b→ (et par rapport auquel le produit vectoriel est perpendiculaire par définition).
Calcul algébrique du produit vectoriel dans un espace de dimension 3 :
par (56) :
a→ x b→ = ( ax * 1→x + ay * 1→y + az * 1→z ) x ( bx * 1→x + by * 1→y + bz * 1→z ) ⇔
... ⇔
a→ x b→ =
( ay * bz - az * by ) * 1→x -
( ax * bz - az * bx ) * 1→y +
( ax * by - ay * bx ) * 1→z
Il existe heureusement une notation mnémotechnique de (68), fondée sur la notion de déterminant (cf. infra #formule-generale-determinant) de a→ x b→ :
a→ x b→ =| 1→x | 1→y | 1→z |
| ax | ay | az |
| bx | by | bz |
... qui est la formulation algébrique standard du produit vectoriel.
NB : on constatera que le changement du signe de 1→y dans le cas du croisement L1-C2 est cohérent avec l'application de la règle de la main droite à 1→x x 1→z.
Interprétation géométrique
Dans le schéma suivant, la partie droite représente le produit vectoriel représenté à gauche, mais cette fois vu à la verticale (⇒ le symbole "pointe de flèche" 🞊 représentant le vecteur du produit scalaire, et déterminé par la règle de la main droite).
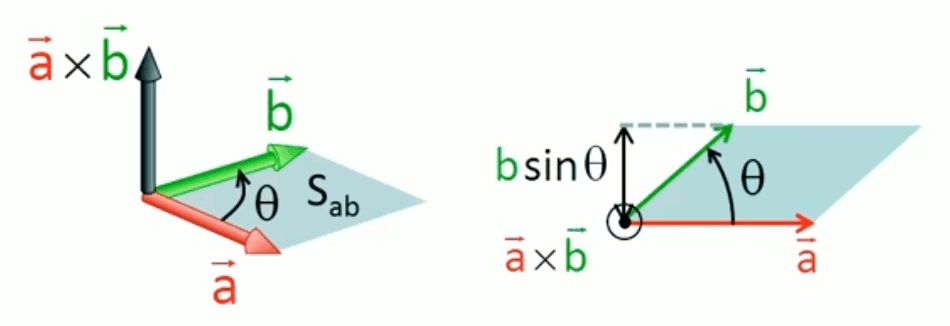
Surface. Il apparaît ainsi que le produit scalaire a→ x b→ = || a→|| * || b→|| * sin(θ) * 1→⊥ (62) correspond à la surface du parallélogramme construit sur les vecteurs a→ et b→ : a→ x b→ = Sab * 1→⊥ où Sab est donc le module du produit vectoriel.
La problématique du calcul de la surface du parallélogramme quelconque est identique à celle du triangle quelconque (revoir supra : #triangle-trapeze).
Volume. Par conséquent, soit un vecteur quelconque c→, il résulte de la propriété ci-dessus que le produit scalaire (par c→) du produit vectoriel a→ x b→, noté ( a→ x b→ ) . c→ et appelé "produit mixte" (prononcer "a croix b fois c"), est tel que :
( a→ x b→ ) . c→ =
Sab * 1→⊥ . c→ =
Sab * c * cos(φ) =
Sab * h
soit le volume du parallélépipède quelconque (c-à-d pas nécessairement rectangle) formé par les angles du produit vectoriel a→ x b→ ) et un angle quelconque c→.
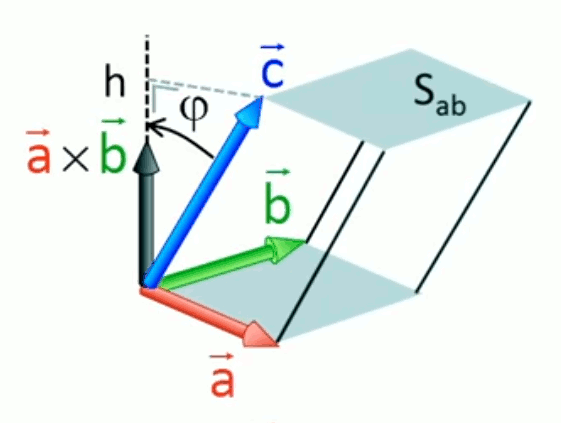
La valeur de ce volume se calcule à partir de (69) : ( a→ x b→ ) . c→ =
| 1→x | 1→y | 1→z |
| ax | ay | az |
| bx | by | bz |
| cx | cy | cz |
| ax | ay | az |
| bx | by | bz |
On démontre cette égalité en remplaçant le déterminant du premier membre par un vecteur quelconque u→ (= a→ x b→), puis en montrant que pour obtenir le produit scalaire de celui-ci avec c→ il suffit de remplacer les coordonnée de 1→ par celles de c→ :
par (56) :
( ux * 1→x + uy * 1→y + uz * 1→z )
.
( cx * 1→x + cy * 1→y + cz * 1→z )
=
ux * cx + uy * cy + uz * cz
et par conséquent, dès lors que cette seconde égalité représente la première (celle avec les déterminants), on constate dans la seconde, que l'expression algébrique du membre de droite (qui correspond au déterminant de droite) s'obtient en remplaçant simplement dans le premier facteur du membre de gauche (qui correspond au déterminant de gauche) les coordonnée de 1→ par celles de c→. Donc le déterminant de droite, c'est bien celui de gauche dont on a remplacé les coordonnée de 1→ par celles de c→.
CQFD
⇒ il reste alors à appliquer la règle de calcul du déterminant, pour obtenir la forme algébrique de produit mixte :
( a→ x b→ ) . c→ =
cx * ( ay * bz - az * by ) -
cy * ( az * bx - ax * bz ) +
cz * ( ax * by - ay * bx )
Équation de la droite
2. Équation paramétrique
3. Équation cartésienne
Introduction à la géométrie analytique
Cette série de vidéos consacrées à l'équation de la droite commence par une question pratique précise : comment donner instructions à une imprimante 3D de tracer un "lieu de points" quelconque ?
Le graphique ci-dessous en illustre deux :
- le segment vert d'équation :
y = ( ay / ax = tgα ) * x
0 < x < ax - le cercle rouge, que l'on peut formuler de deux façons :
y = +/- √(32 - x2) (24)
-3 < x < 3
N.B. On notera l'indication +/-, pour prendre en compte que y devient négatif dès que α dépasse π/2. C'est pourquoi on préférera généralement la formulation trigonométrique : y = 3 * sinα (31)
x = 3 * cosα
0 < α < 2π
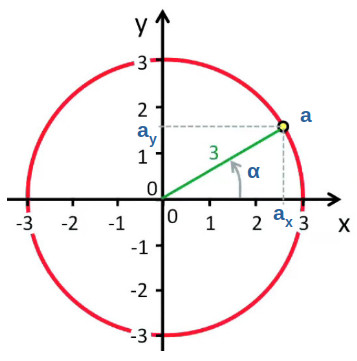
On constate une différence importante entre les deux formulations du cercle : la seconde fait apparaître un paramètre : l'angle α (c'est pourquoi elle est qualifiée de "paramétrique", la première étant la forme "cartésienne" car elle utilise les coordonnées cartésiennes).
Équation paramétrique
Soit deux points a et b définis par leur vecteurs position a→ et b→, le segment entre les points a et b est alors représenté par le vecteur b→ - a→ (55). De la même manière on peut définir le vecteur "courant" r→ tel que :
r→ = a→ + λ * ( b→ - a→ )
λ ∈ [0,1]
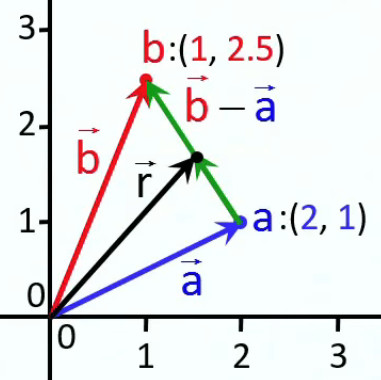
Ainsi en faisant varier la valeur de λ on dessine le segment de droite entre les points a et b. Et l'on peut même dessiner un segment de longueur arbitraire en remplaçant la contrainte [0,1] par la contrainte correspondante. Il reste maintenant à déterminer les composantes (x,y) du vecteur courant r→ :
x = ax + λ * ( bx - ax )
y = ay + λ * ( by - ay )
x = ax
y = ay + λ * ( by - ay )
de sorte que y devient le paramètre ultime : c'est sa variation qui dessine la droite.
Cependant, plutôt que par deux points, une droite peut être définie par un point et un angle, celui-ci étant déterminé au moyen d'un "vecteur directeur" v→, de coordonnées (vx,vy) = (1,tgα), auquel la droite passant par le point doit être parallèle.
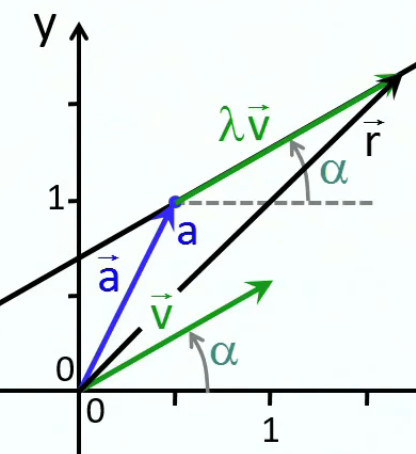
Il suffit alors de translater ce vecteur directeur à la suite du vecteur a→, où il va jouer le rôle du vecteur b→ - a→, de sorte que l'équation paramétrique :
r→ = a→ + λ * ( b→ - a→ )
devient :
r→ = a→ + λ * v→
⇒ exprimée en fonction de composantes des vecteurs :
x = ax + λ * vx
y = ay + λ * vy
Équation cartésienne
Nous allons développer l'équation générale de l'équation cartésienne de la droite, à partir de sa forme paramétrique (que nous venons de développer supra, et où nous remplaçons ici a→ = (ax,ay) par p→ = (px,py) ). Pour cela on va substituer λ entre les deux égalités de (72) de sorte que l'on exprime y en fonction de x :
( x - px ) / vx = ( y - py ) / vy ⇔
y = vy / vx * x + py - vy / vx * px
N.B. Il s'agit bien de la forme habituelle (qui n'est pas la forme générale) :
y = a * x + b
où
• a = vy / vx
• b = py - vy / vx * px
Mais cette forme n'est pas l'expression générale de l'équation cartésienne de la droite, car elle ne permet pas d'exprimer la droite verticale : en effet dans ce cas la pente vy / vx est infinie ⇒ (73) donne y = ∞ - ∞, qui est indéterminé. Pour contourner ce problème on multiplie les deux membres de (73) par vx ⇒ on obtient l'équation cartésienne sous sa forme générale :
- vy * x + vx * y = - vy * px + vx * py
N.B. Qui est de type :
a * x + b * y = c
où
• a = - vy
• b = vx
• c = - vy * px + vx * py
Et l'on constate que cette forme générale de l'équation cartésienne permet bien de prendre en compte le cas d'une droite verticale c-à-d telle que vx=0 ⇒ (74) donne x=px
La façon la plus simple de dessiner une droite à partir de son équation cartésienne a * x + b * y = c est de calculer le point ou les deux points d'intersection avec les axes X et Y : il suffit de poser x=0 et de calculer la valeur correspondante de y (=c/b), puis de poser y=0 et de calculer la valeur correspondante de x (=c/a).
Forme
vectorielle
On va maintenant développer une interprétation géométrique de l'équation cartésienne, sous forme vectorielle. Pour ce faire la contrainte imposée au vecteur "courant" r→ relativement au vecteur "position" p→ n'est plus le couple (paramètre λ, vecteur "directeur" v→) mais un vecteur "normal" n→ (perpendiculaire à la droite) :
n→ . r→ = n→ . p→ ⇔
n * r * cos(φ) = n * p * cos(θ)
soit un produit scalaire signifiant que p→ et r→ on la même projection sur n→.
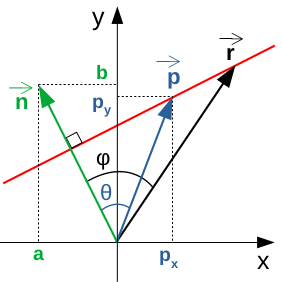
Enfin soient :
n→ = (a, b),
p→ = (px, py) et
r→ = (x, y)
⇒
par (59) :
a * x + b * y = a * px + b * py
L'on peut alors comparer (76) à (74) pour constater que les coordonnées du vecteur normal n→ = (a, b) ont remplacé les coordonnées (-vy, vx) ... qui sont bien celles du point déterminé par la rotation à 90° du vecteur directeur v→ !
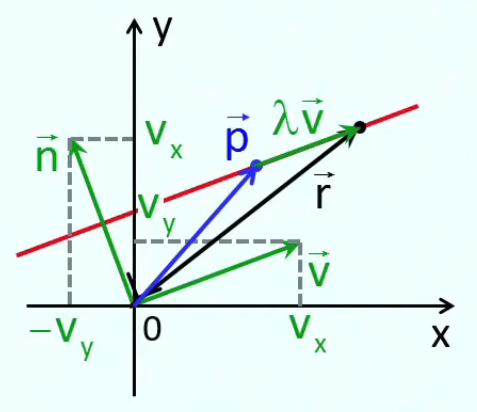
Cette forme vectorielle de l'équation paramétrique sera très utile pour le développement de l'équation du plan dans l'espace à trois dimensions.
Équation du second degré
Soit l'équation polynomiale de degré n :
∑i=0n ai * x i = 0
Si n=2 on obtient le polynôme du second degré a0 + a1 * x + a2 * x2, que l'on écrit plus souvent sous la forme a * x2 + b * x + c (forme "standard").
Si a * x2 + b * x + c = 0 est l'équation polynomiale du second degré, on pourrait se demander ce qu'est a * x2 + b * x + c = d. La réponse est que « c'est également une équation polynomiale du second degré » :
a * x2 + b * x + c = d ⇔
a * x2 + b * x + ( c - d ) = 0 ⇔
Résolution
algébrique
Pour trouver la solution de l'équation du second degré a * x2 + b * x + c = 0, c-à-d exprimer x en fonction de la valeur des paramètres, n'est pas évident. Une première tentative conduit à :
x = √( - ( b * x + c ) / a ) ⇒
Comment faire passer le x de droite dans le membre de gauche ...?
Voici une méthode en quatre étapes pour y arriver :
-
isoler x :
a * x2 + b * x + c = 0 ⇒
en posant : b * x + c = - h ⇒
a * x2 - h = 0 ⇔ x = +/- √ ( h / a ) -
passer à la forme canonique :
dans la relation biunivoque ci-dessus, on remplace x par x-e ⇒
a * ( x - e )2 - h = 0 ⇔ x = e +/- √ ( h / a )
-
calculer les équivalences en e et h, entre formes canonique et standard :
a * ( x - e )2 - h = 0 ⇔ (← forme canonique)
a * x2 - 2 * a * e * x + a * e2 - h ⇒
par comparaison avec :
a * x2 + b * x + c (← forme standard)
on voit que :
b = - 2 a * e
c = a * e2 - h
⇔
e = - b / ( 2 * a )
h = a * e2 - c = ⇒ h = b2 / ( 4 * a ) - c
-
Substituer les valeurs de e et h dans la solution canonique :
x = e +/- √ ( h / a ) (77)
x = - b / ( 2 * a ) +/- √ ( b2 / ( 4 * a2 ) - c / a ) ⇔
x = [ - b +/- √ ( b2 - 4 * a * c ) ] / ( 2 * a )
PS : ces deux valeurs (notez le +/-) sont appelées "racines de l'équation du second degré".
Pour qu'une solution existe il faut que la partie en racine carrée soit non négative : b2 - 4 * a * c ≥ 0 (car il n'existe pas de racine carrée d'un nombre négatif puisque tout carré est positif). Cette partie en racine carrée est appelée "discriminant" de l'équation (et notée Δ) car elle différencie les valeurs respectives des deux "racines" (on ne dit pas "solution" car c'est leur ensemble qui constitue la solution).
Interprétation
géométrique
Commençons par rappeler la différence entre le graphe y = a * x2 + b * x + c (la courbe rouge, telle que x est en abscisse et y(x) = a * x2 + b * x + c en ordonnée), et le cas particulier y = a * x2 + b * x + c = 0 déterminant les deux "zéros" du polynôme (les deux points jaunes).
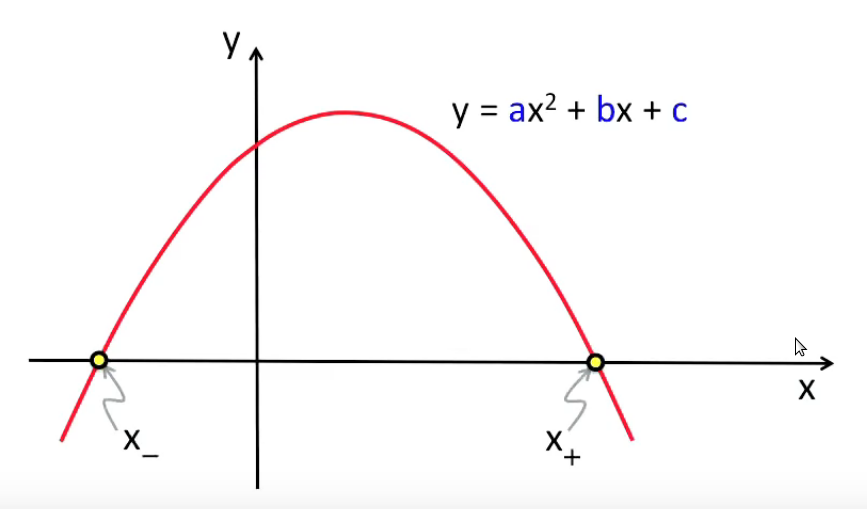
Poussons maintenant l'analyse géométrique en observant l'effet de divers paramétrages du polynôme, c-à-d l'effet de diverses valeurs des paramètres a, b et c (⇔ diverses valeurs des paramètres h, e et a de la forme canonique (77) ) sur le graphe de la fonction polynomiale y = a * x2 + b * x + c. Commençons par le cas de référence, tel que b=c=0 (⇔ h=e=0) ⇒ y = a * x2. Ensuite nous étudierons les cas où h puis e ne sont plus négatifs.
Le graphe suivant est illustre le cas de référence pour a=1/2.
Levons maintenant la restriction h=0 ⇒ y = a * x2 - h. Nous voyons que cela correspond à un mouvement vertical de la parabole vers le bas.
On voit alors (graphique ci-dessous) apparaître les "zéros" de la fonction. L'équation canonique x = e +/- √ ( h / a ) (77) montre que la condition nécessaire est h/a ≥ 0 .

Levons maintenant la restriction e=0 ⇒ y = a * ( x - e )2 - h, ce qui correspond à un mouvement horizontal de la parabole. Pour le comprendre il suffit de poser x=e ⇒ y=-h ⇔ la parabole se déplace horizontalement et vers la droite. Il en résulte que l'axe de symétrie est passé de x=0 à x=e.
On voit enfin que la valeur de a détermine l'ouverture de la parabole : plus a est grand, plus la valeur de y est élevée pour un x donné.
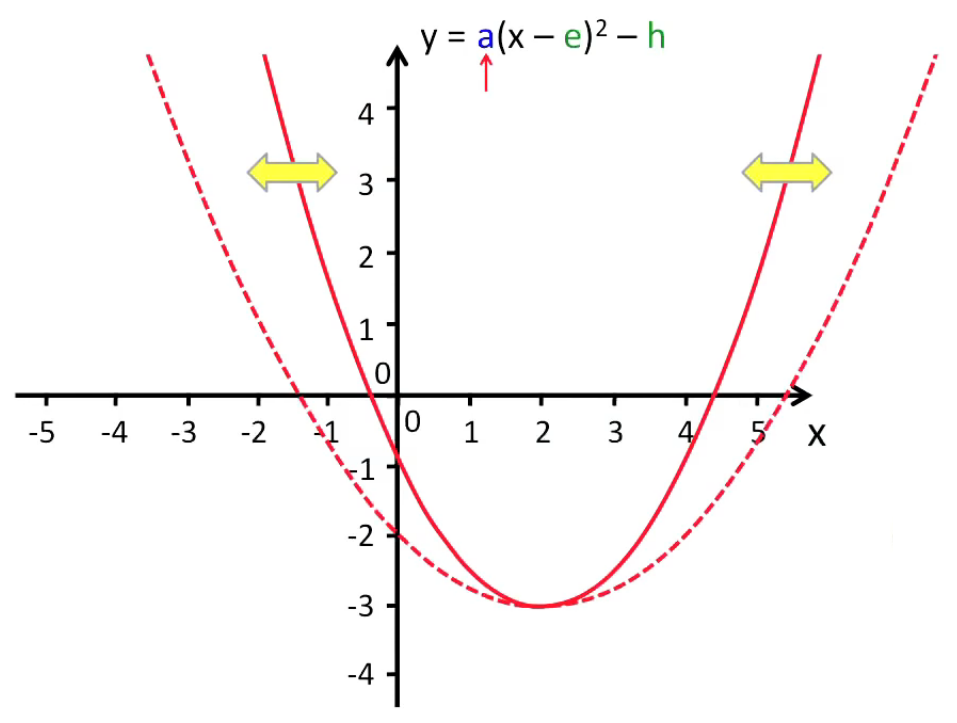
En résumé pour la forme canonique y = a * ( x - e )2 - h :
- h détermine le minimum de la parabole, et donc le déplacement vertical ;
- e détermine la position de l'axe de symétrie, et donc le déplacement horizontal ;
- a détermine l'ouverture de la parabole.
Le graphique suivant exprime la situation cette fois en termes standards.
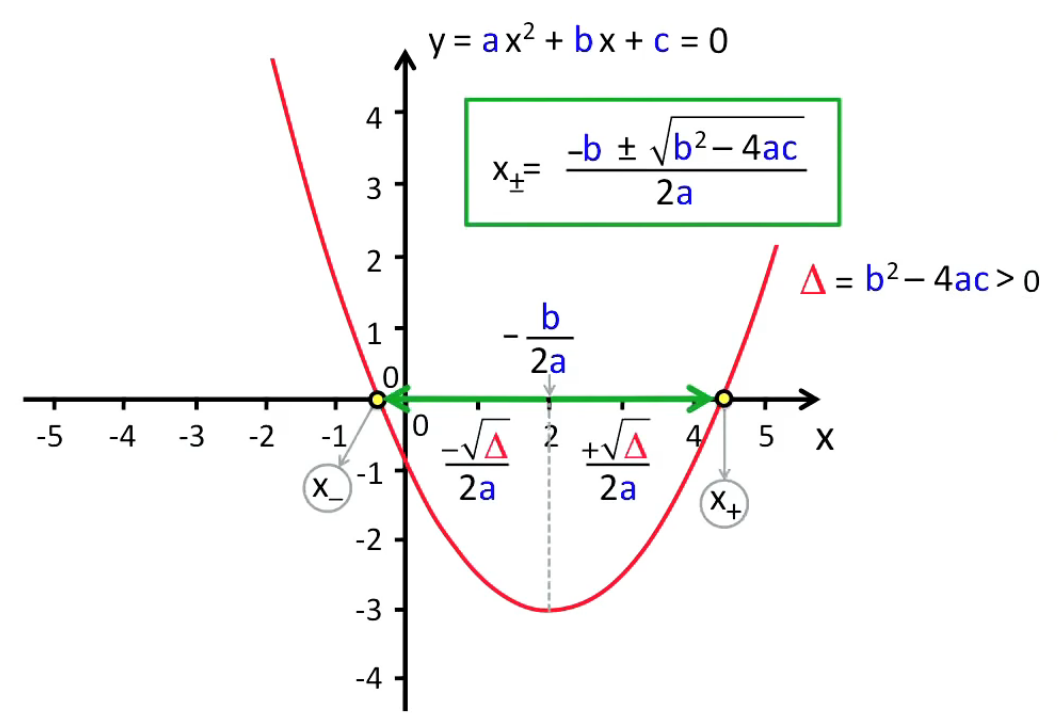
Distinguons dans la solution encadrée en vert les deux membres de l'addition/différence : le membre de gauche (-b/(2a) c-à-d e) détermine l'axe de symétrie, tandis que le membre de droite détermine l'ouverture de la parabole. Quant à la position du minimum de la parabole, elle est fonction du signe du discriminant Δ :
- Δ > 0 ⇔ minimum en-dessous de l'axe horizontal ⇔ deux "zéros" ;
- Δ= 0 ⇔ minimum sur l'axe horizontal ⇔ un seul "zéro" ;
- Δ < 0 ⇔ minimum au-dessus de l'axe horizontal ⇔ pas de "zéro".
Illustration
La trajectoire balistique d'un corps lancé dans l'espace en présence de gravitation est donnée par l'expression du graphique ci-dessous, qui est bien un polynôme du second degré. On notera le signe négatif lié à la gravitation g (puisque celle-ci est orientée vers le bas). Le signe du paramètre a dans y(x) = a * x2 + b * x + c étant ainsi négatif la parabole est bien concave. Il y a cohérence entre formulation théorique et réalité physique.
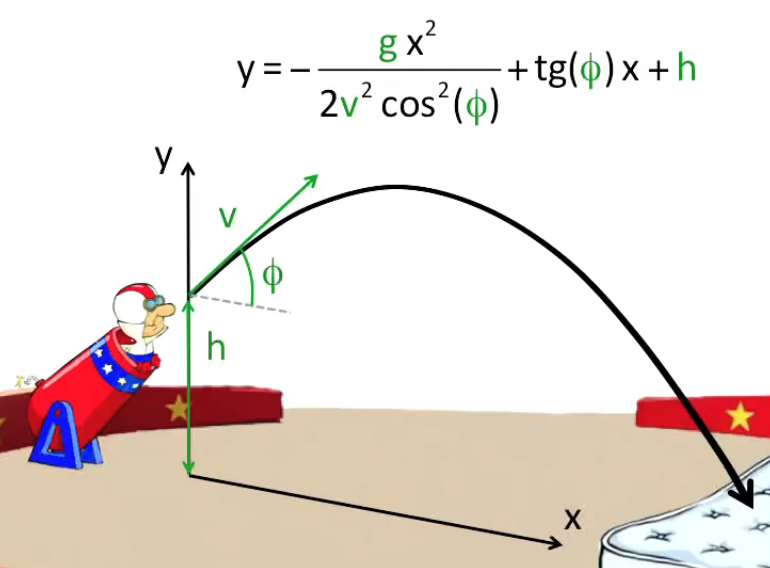
On veut calculer l'endroit où placer le matelas, c-à-d la valeur de x correspondant à y=0. L'équation a * x2 + b * x + c = 0 correspond donc à la problématique. La solution se trouve dans la valeur des racines dont nous avons calculé la formule. Les valeurs des paramètres g, v, φ et h étant connues, il en va de même pour les paramètres correspondants a, b et c. Il reste à calculer la valeur de x ... en veillant à utiliser les mêmes unités de longueur (PS : on notera à cet égard que la tangente n'a pas de dimension ⇒ ok pour x1).
Mais il reste à interpréter correctement les résultats, c-à-d en fonction de la réalité physique. En l'occurrence il apparaît qu'une des deux racine est nécessairement négative (puisqu'on a placé le zéro des abscisse au niveau du canon) et ne correspond ici à aucune réalité physique.
On va enfin calculer la hauteur maximale H que le clown va atteindre afin de vérifier que le chapiteau est suffisamment haut. L'équation du second degré correspondant à cette problématique est :
a * x2 + b * x + c = H ⇔
a * x2 + b * x + ( c - H ) = 0
Le graphique suivant montre que c'est évidemment au sommet de cette courbe que la hauteur est maximale. Or ce sommet correspond aux cas où il n'y a qu'une seule racine c-à-d tel que le discriminant est nul (NB : remplacer c par c'=c-H dans la formule du discriminant).