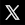V. Dynamique
Cinématique : MRU et MRUA
 Vidéos Clipedia :
Le mouvement : position et déplacement //
Le mouvement : fonction et graphe // Le mouvement rectiligne uniforme : introduction // Le mouvement rectiligne uniforme : généralisation
Vidéos Clipedia :
Le mouvement : position et déplacement //
Le mouvement : fonction et graphe // Le mouvement rectiligne uniforme : introduction // Le mouvement rectiligne uniforme : généralisation
Mouvement rectiligne uniforme (MRU) :
La vitesse v est la distance xt - x0 parcourue durant le temps t :
v = ( xt - x0 ) / t ⇔
xt = x0 + v * t ⇔
NB : v est la "pente" de la droite x(t)
xt - x0 = v * t ⇒
xt - x0 est la surface verte en dessous de la droite vt = v0
Lecture du graphique. La valeur de la longueur xt - x0 hachurée en vert (exprimée en m) est égale à la valeur de la surface verte, c-à-d au produit de sa hauteur v0 (en m/s) et de sa longueur t (en sec.), de sorte que son unité est bien m/s*s=m.
 Vidéos Clipedia :
Le Mouvement Rectiligne Uniformément Accéléré : introduction // Le Mouvement Rectiligne Uniformément Accéléré : généralisation
Vidéos Clipedia :
Le Mouvement Rectiligne Uniformément Accéléré : introduction // Le Mouvement Rectiligne Uniformément Accéléré : généralisation
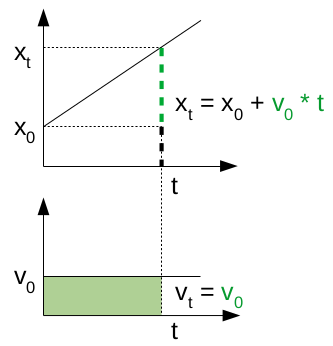
Mouvement rectiligne uniforme accéléré (MRUA) :
L'accélération a est la vitesse vt - v0 acquise durant le temps t :
a = ( vt - v0 ) / t ⇔
⇒ l'accélération exprime la progressivité dans la modification d'un mouvement.
vt = v0 + a * t ⇒ par (162) :
( xt - x0 ) / t = v0 + a * t ⇔
xt - x0 = v0 * t + [ ( v0 + a * t - v0 ) * t ] / 2 ⇔
NB : [ ( v0 + a * t - v0 ) * t ] / 2 est la moitié du rectangle au-dessus du rectangle vert
xt - x0 = v0 * t + a * t2 / 2 ⇔
xt = x0 + v0 * t + a * t2 / 2
⇔
xt = x0 + ( v0 + vt ) / 2 * t
NB : ( v0 + vt ) / 2 est une mesure moyenne de la vitesse.
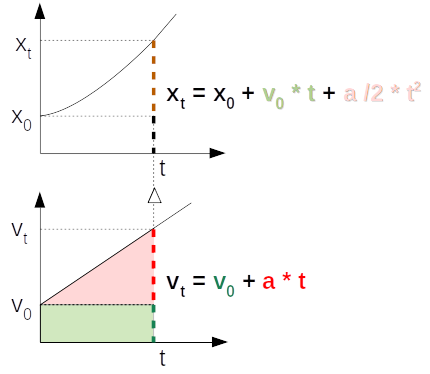
Lecture du graphique. La surface triangulaire rouge c'est bien la moitié de la surface rectangulaire base * hauteur = t * ( a * t )) ⇒ elle vaut donc bien 1/2 * a t2. On obtient alors la valeur de xt en ajoutant à celle de x0 la valeur de la surface totale en-dessous de la droite vt ⇔ la distance parcourue xt - x0 (ligne hachurée en brun) est égale à la valeur de cette surface.
Dans la section consacrée au calcul intégral nous avons calculé qu'effectivement :
xt - x0 = ∫ 0 t v(t') * dt' = v0 * t + a/2 * t2 (cf. /algebre#exemples-integrales).
Le graphique ci-dessous détaille la composition de la distance x(t). La composante 1/2 * a * t2 s'ajoute à la composante v0 * t, qui est mesurée à partir de x0.
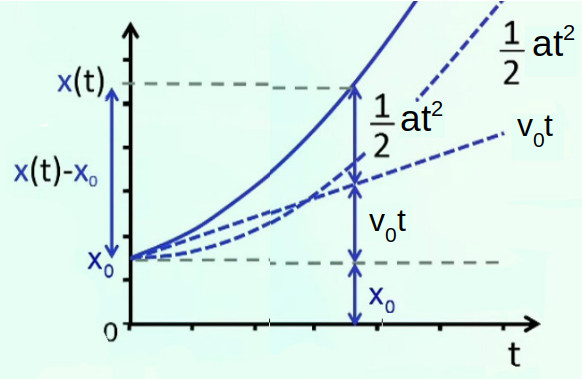
Les passages de la vidéo "Le Mouvement Rectiligne Uniformément Accéléré : généralisation" consacrés à l'interprétation de ces résultats en termes de référentiels me paraissent confus. Heureusement ces passages n'ajoutent rien de formel aux équations ci-dessus. Je ne mentionnerai donc ici que leur conclusion en termes de contributions des deux référentiels :
| v(t) = | v0 | + | a * t | (163) |
| x(t) = | x0 + v0 * t | + | 1/2 * a * t2 | (164) |
| Contrib. : | MRU | + | MRUA |
... dont l'avant dernier graphique donne l'interprétation géométrique.
NB : à partir des équations du MRUA on retrouve celles du MRU en posant a=0.
Cette analyse cinématique fait abstraction des masses qui caractérisent les corps, ainsi que les éventuelles forces qu'ils peuvent subir ou exercer en relation avec d'autres corps (on parle alors de cinétique). Cela est l'objet des sections suivantes.
Force et mouvement
2. Inertie
3. Loi de Newton
Relativité
Le principe de relativité affirme l'équivalence entre MRU et repos : ils constituent tous les deux un référentiel inertiel c-à-d tel que la vitesse est constante en direction et en norme (NB : une vitesse nulle n'est qu'un cas particulier de vitesse constante).
Pour comprendre ce principe à priori peu intuitif, commençons par étudier de plus près la notion de mouvement. Un mouvement est un changement de position d'un corps au cours du temps ⇒ par v = ( xt - x0 ) / t (162) le mouvement est dont intrinsèquement lié à la notion de vitesse (N.d.A. : on pourrait même définir le mouvement par sa vitesse). Par conséquent, poser la question de ce qui cause le mouvement, c'est poser la question de ce qui provoque un changement de vitesse. On pourrait donc penser que la vitesse d'un mobile serait proportionnelle à la force qui lui est appliquée : v ∝ F ?
En fait lorsque je lance une pierre, la force que j'exerce sur elle n'opère plus sur la pierre après qu'elle a quitté ma main. Et si la pierre finit par s'arrêter c'est à cause des forces de frottement. On peut expérimenter cela dans l'espace (qui est vide, donc sans frottements) : si on lance un objet, il suit sans fin la même direction, et à vitesse constante. Sa direction et vitesse ne seront modifiées que par l'action de forces extérieures.
Dès le 17° siècle Galilée avait déjà observé, avec son expérience d'un bille dévalant un plan incliné suivi d'un plan horizontal, que le trajet total de la bille augmentait d'autant plus qu'on lissait la surface de la bille et des plans, c-à-d qu'on réduisait les forces de frottement (et cela avec la même force initiale qui est la force d'attraction terrestre, la bille étant simplement lâchée au sommet du plan incliné).
Dans cette situation "immuable sauf forces extérieures" on dit que le corps est "inerte" ou encore "au repos". Mais cela signifie-t-il qu'il est immobile ? Réponse : cela est relatif ! Pour le comprendre imaginons un train en MRU, et ne subissant aucune force de frottement ⇒ la seule force qu'il subit est la force de pesanteur. Une balle lâchée dans ce train en mouvement tombe à la verticale devant l'expérimentateur ⇔ dans un train ou dans son salon, le lâcheur de balle observe le même phénomène. On en conclut que mouvement (rectiligne et uniforme) et repos sont relatifs, c-à-d que l'on peut considérer aussi bien que c'est le train qui est en mouvement et la Terre (le salon) qui est au repos, ... ou bien que c'est au contraire le train qui est au repos et la Terre en mouvement. Nous avons d'ailleurs tous expérimenté ce phénomène : assis dans le train dans une gare nous pensons qu'il démarre enfin, puis découvrons qu'en réalité c'est le train d'à côté qui démarre (dans l'autre sens). Et si je laisse tomber un objet dans le train en mouvement, il tombe de la même manière que si je faisais la même expérience au buffet de la gare (... pour autant que le train avance à vitesse constante et pas en virage, c-à-d en MRUA).
Par contre, lorsque l'avion prend son envol en accélérant, nous sommes poussés contre le dossier du siège. Pour expliquer cela il faut d'abord introduire le principe d'inertie, et ensuite celui de masse.
Inertie
Le principe d'inertie (aussi appelée "première loi de Newton) affirme que pour changer de mouvement (c-à-d de vitesse) un corps doit subir une force.
Référentiel
inertiel
La notion de relativité requiert de préciser dans quel référentiel une mesure est effectuée. Si du quai d'une gare j'observe tomber une balle lâchée dans un train en MRU, je n'observe pas la même trajectoire (une courbe) que celle observée par l'expérimentateur situé dans le train (une droite), bien que ces deux trajectoires dépendent de la même équation. La raison en est que dans le référentiel de la gare, la balle a une vitesse non nulle (celle du train), tandis que dans le référentiel du train sa vitesse est nulle. Et inversement, en raison du principe de relativité, si la balle est lâché par la personne sur le quai, l'observateur situé dans le train constatera une trajectoire courbe car dans (relativement à) son référentiel qu'est le train, la balle a une vitesse non nulle. Cela illustre bien le principe de relativité : chaque observateur constate des trajectoires différentes selon son propre référentiel, mais les observations obéissent aux mêmes lois physiques (les équations de la cinématique) dans chaque référentiel inertiel.
N.d.A. Une voiture qui démarre puis accélère jusqu'à se maintenir à une vitesse constante, puis freine jusqu'à s'arrêter subit quatre changements de référentiel :
MRU(v=0) ⇒ MRUA(a>0) ⇒ MRU(v=vc)⇒ MRUA(a<0) ⇒ MRU(v=0)
parties vertes : ∄ force ;
partie rouge : ∃ force.
Le principe de relativité vaut également pour les notions de décélération et accélération. Ainsi lorsque le pilote freine relativement au référentiel de la Terre, il démarre (vers l'arrière) dans celui de son véhicule qui était en MRU : il quitte le référentiel de son véhicule pour aller vers celui de la terre. Et inversement : lorsqu'il accélère relativement au référentiel de la Terre, il freine (vers l'arrière) dans le sien qu'il quitte.
Un corollaire du principe d'inertie est que la force engendre l'accélération (négative en cas de décélération). C'est Issac Newton, né l'année du décès de Galilée, qui va formuler cette relation en introduisant la notion de masse.
Loi de Newton
Un corps ne doit pas nécessairement subir une force pour être en mouvement (principe d'inertie), mais par contre la modification d'un mouvement ou du repos implique l'action d'une force. La (seconde) loi de Newton (la première étant la loi d'inertie) définit et formule cette force : exercer une force F c'est imprimer une accélération a au déplacement d'une masse m :
F = m * a [kg * m / s2 = N]
où le newton (N) est donc la force requise pour imprimer à une masse de 1kg une accélération de 1 m/s2.
Poids vs masse. Il ne faut pas confondre la masse (en kg, unité de masse) avec le poids (en N, unité de force), qui est la force subie par une masse dans un champ gravitationnel. Dans le champ gravitationnel terrestre, qui est tel que a≈10m/s2, une masse de 1kg subit donc une force de gravitation FG = 1 * 10 = 10N. La confusion vient du raccourci consistant à parler d'un poids de x "kilos" alors qu'il s'agit en réalité d'un poids de x "kilogramme-force", ou plus exactement x*10 newtons. Plus précisément : 1N=102g.
Pour vérifier la linéarité effective de la relation (168) imaginons un chariot propulsé sur un rail, et faisons abstraction de toutes forces de frottement. Si le chariot subit une force de propulsion constante, sa vitesse augmente constamment, et cela à un rythme constant. Cela se démontre géométriquement en additionnant, pour une courbe quelconque de la fonction v(t) sur un intervalle Δt, une suite de pentes Δv/Δt telles que Δt, et donc Δv, sont arbitrairement petits.
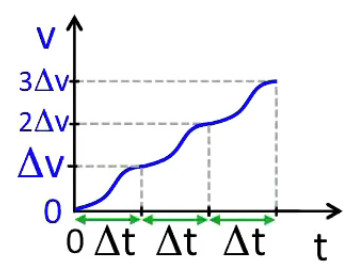
Il apparaît alors que dv/dt, qui est précisément l'accélération (162), est constante. C'est donc l'accélération, et non la vitesse, qui est proportionnelle à la force exercée : a ∝ F.
Nous venons ici d'effectuer une mesure de la force en mesurant la modification de mouvement (c-à-d de vitesse). Une autre manifestation de la force est la modification de forme, que l'on peut mesurer au moyen d'un dynamomètre. La force est ici mesurée par l'allongement d'un ressort dont la raideur est étalonnée : force = raideur × allongement.
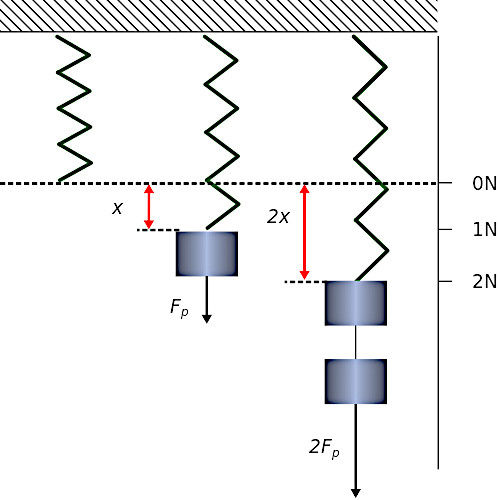
Ceci nous permet de compléter notre relation : l'accélération est proportionnelle à la force (avec laquelle elle augmente) et à la masse (avec laquelle elle diminue pour une force donnée) : a ∝ F, 1/m ⇔ F ∝ m, a ⇒ la façon la plus simple de définir la force est alors F = m * a, ce qui est confirmé par l'expérience de pensée consistant à attacher deux chariots propulsés, de sorte que l'on mesure bien que 2 * F = ( 2 * m ) * a.
La loi d'action-réaction, ou "troisième loi de Newton" (N.d.A. : qui est un corrolaire de la loi de conservation de l'énergie) énonce que toutes les forces apparaissent par couple de forces opposées (N.d.A. : toute action entraîne une réaction en sens contraire et de même ampleur).
La force que subit la particule 1 en raison de la présence de la particule 2 (F→1,2) est égale à l'opposé de la force que subit la particule 2 en raison de la présence de la particule 1 (F→2,1) :
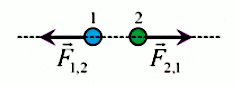
F→1,2 = - F→2,1
Exemples :
- soit l'accélération de pesanteur terrestre gT ≈ 9,8 mT/s2 ⇒ pour tenir/soulever dans ma main une masse de 1kg je dois exercer une force de 9,8 N, qui est le poids de cette masse c-à-d sa force d'inertie ;
- le passager en apesanteur dans un véhicule spatial qui démarre (MRUA) donne l'impression d'être projeté contre la paroi arrière du véhicule, mais c'est en réalité celle-ci qui s'avance vers lui, jusqu'au moment où il est rattrapé, ce qui marque son passage d'un référentiel inertiel à celui que constitue le véhicule; à partir de ce moment le passager subit deux forces : la force motrice qui propulse le véhicule en avant, et la force d'inertie, opposée, qui le maintient contre la paroi jusqu'à ce que la vitesse devienne constante (MRU) moment à partir duquel il retourne en apesanteur.
Selon Einstein cette force d'inertie qui maintient le passager non attaché contre la paroi est de même nature que la force de gravitation : c'est le principe d'équivalence, point de départ de la théorie de la relativité générale. On peut ainsi considérer que la surface de la Terre avance avec une accélération a=g. Autrement dit, la force gravitationnelle ne serait rien d'autre qu'une force d'inertie.
La Terre n'est donc pas un référentiel fixe.
Et on a là l'explication de la "chute des corps" avec la même accélération, indépendamment de leur masse : en réalité il ne s'agit pas de leur accélération mais de celle de la Terre !
En vertu du principe d'équivalence, en sautant ou tombant je passe dans un référentiel inertiel ⇔ je ne subis plus d'accélération ⇔ par (168) : Poids = m * g = m * 0 ⇔ je suis en apesanteur ⇔ "on ne tombe pas, on est rattrapé par la Terre" ⇒ il n'y a aucune raison pour que deux corps ne soient pas rattrapés en même temps, même si leurs masses diffèrent. CQFD par raisonnement logique. Mais des démonstrations expérimentales ont aussi été réalisées, comme le montre la vidéo suivante.
Démonstration expérimentale (4m41s)
Cette interprétation de Terre en MRUA permanent est pour le moins contre-intuitive puisqu'elle vaut pour tous les points de planète, donc également pour deux points diamétralement opposés : comment la Terre peut-elle se déplacer en MRUA dans toutes les directions à la fois ... ? Nous verrons dans la section consacrée aux ondes gravitationnelles que cette explication contre-intuitive est cependant cohérente si l'on introduit dans le raisonnement la notion de courbure de l'espace-temps à proximité d'un corps de masse non nulle. Malheureusement la complexité de cette théorie fait que dans les écoles est enseignée l'interprétation fausse de la "chute" des corps, plus intuitive que celle du rattrapage des corps par la Terre qui "monte" ...
Force et pression
2. Pression atmosphérique
3. Pression hydrostatique
Pression dans les solides
C’est la pression que la force engendre, et non pas la force elle-même, qui détermine la façon dont un matériau réagit sous la contrainte. Ainsi les fibres du bois d'un plancher se partagent le poids qu'elles supportent.
La pression c'est la force par unité de surface : Pression = Force / Surface [N/m2]
La résistance des matériaux est caractérisée par la pression. Ainsi au moyen d'une presse on peut mesurer la limite de rupture des fibres d'un bloc de bois (dans le cas du pin : 50 MN/m2 = 50 N/mm2 = 5 kgf/mm2. La pression exercée par un talon aiguille de 5mm de côté, et supportant une personne de 70kg, exercera une pression de 700N/25mm2=28N/mm2, ce qui n'étant pas très éloigné de la limite de rupture du pin explique l'emprunte du talon sur un plancher de pin.
Si la résistance du bois est de 1 (référence sans dimension), on a 5 pour l'acier, 20 pour la toile d'araignée et 1000 pour le béton. Il s'agit là évidemment d'ordres de grandeurs, car il y a des qualités différentes de chacun des ces matériaux.
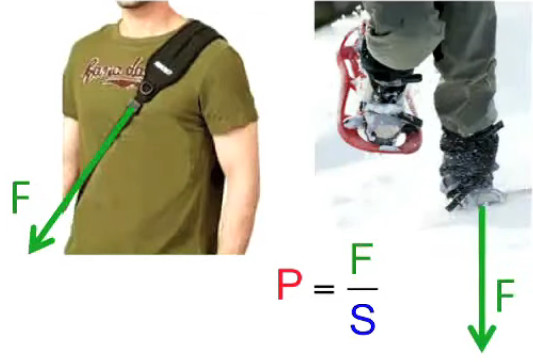
Les illustrations suivantes montrent deux applications technologiques fondées sur (170). Elles ont pour principes de répartir la force sur une certaines surface afin de réduire la pression par unité de surface : on s'enfonce moins dans la neige avec des raquettes, et la sensation de poids d'un sac en bandoulière est réduite par la largeur de la sangle.
Compression et traction sont très semblables : on parle ainsi de la pression comme une "contrainte de traction". Cela est illustré par les atomes d'un cristal de fer, qui s'organisent spatialement comme dans le schéma ci-dessous (NB : l'organisation est en 3D, contrairement à cette illustration en 2D).
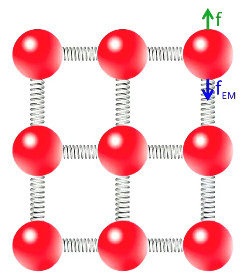
Sous l'effet de l'agitation thermique, ces atomes oscillent autour de leur position de repos. Mais globalement la structure est (très) stable, en raison de complexes interactions électromagnétiques, que l'on pourrait représenter par des ressorts. Un ressort ni comprimé ni tendu est en position de repos. L'image suivante illustre l'action d'une force de traction verticale contre la force de cohésion électromagnétique, à partir de la position de repos. Dans le cas d'une force de compression verticale, les deux flèches seraient dirigée l'une vers l'autre.
Cette notion de traction est illustrée par l'exemple du muscle. Il est constituée d'un ensemble de fibres dont les molécules peuvent se raccourcir selon des signaux nerveux envoyés par le cerveau. Un muscle fonctionne en traction, c'est donc bien une contrainte de traction qui est ainsi exercée.
On notera que la force d'un muscle n'est pas nécessairement proportionnelle à son volume mais à sa surface transverse.
Pression atmosphérique
Il est possible de sentir l'existence de l'air en bougeant rapidement un bras dans un mouvement de va et vient : on sent alors "le vent" sur la surface de notre peau. Cette sensation est l'effet des molécules constitutives de l'air, entrant en contact avec les cellules perceptives situées à la surface de la peau. L'air est un mélange gazeux dont les molécules sont essentiellement l'azote (78%) et l'oxygène (21%), plus d'autres molécules, dont le dioxyde de carbone (CO2 : 0,04%) [source].
Ces molécules sont continuellement agitées : c'est l'agitation thermique. L'énergie thermique est l'énergie cinétique d'agitation microscopique d'un objet, qui est due à une agitation désordonnée de ses molécules et de ses atomes. Plus la température est élevées, plus la vitesse d'agitation est élevée. Or à une température ambiante de 20 degrés la vitesse moyenne de ces particules de l'air est de 500 m/s (donc dans le vide), soit 1.800 km/h !
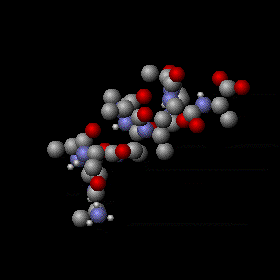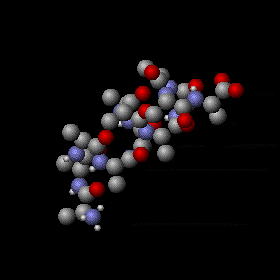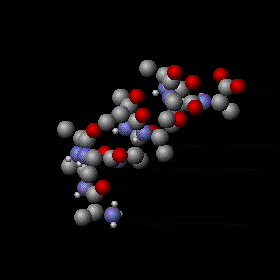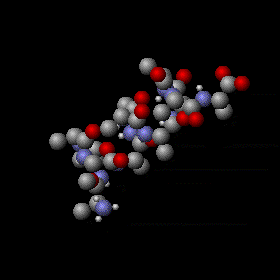
Mouvement thermique d'un segment de molécule d'une protéine.
Par conséquent, sur une paroi quelconque placée dans un milieu non vidé de son air, il y a en permanence des molécules de l'air qui viennent frapper la paroi. On peut considérer que ces forces d'impact s'additionnent et se répartissent sur l'ensemble de la paroi (et cela sera est d'autant plus vrai que l'on observe le phénomène à une grande échelle).
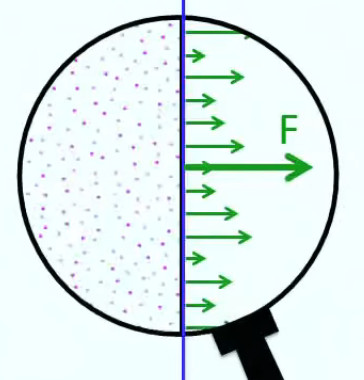
Et plus la surface est grande, plus cette force globale est grande (dès lors que celle-ci est proportionnelle au nombre de particules considérées). Le coefficient de proportionnalité entre force et surface c'est précisément ce qu'on appelle la "pression". On retrouve donc bien Pression = Force / Surface (170).
La pression exercée par un gaz sur son environnement caractérise donc ce gaz, relativement à d'autres gaz. Par conséquent la connaissance de la pression d'un gaz permet, grâce à (170), de calculer la force qu'il exerce sur une surface.
Notons que la force exercée par cette pression est dirigée perpendiculairement à la paroi, toujours en raison de l'approche moyenne des impacts causés par (ou plutôt expression de) l'agitation thermique. Et cela vaut quelle que soit l'orientation de la paroi. On dit ainsi que la pression est "isotrope" (par opposition à "vectorielle").
Dans la section consacrée aux gaz parfaits nous étudierons la relation de proportionnalité entre pression, nombre de particule (P∝N) et température (P∝T).
Pour étudier la pression atmosphérique, il faut faire référence à la théorie mécanique de Newton qui montre que la force moyenne exercée sur le sol par une balle qui rebondit est égale à la force exercée sur le sol par une balle identique qui ne rebondit pas, soit le poids de celle-ci (m*g). Par conséquent, la colonne d'aire délimitée par une surface S au sol exerce sur celle-ci une force M*g où M est la masse des particules constituant cette masse d'air. On a pu ainsi calculer que la pression atmosphérique, c-à-d la pression exercée par l'atmosphère (dont la hauteur est d'environ 100km : u delà on ne trouve quasiment plus aucune molécule constitutive de l'air) sur une surface de 1m2 (au niveau de la mer) vaut : Patm = M * g / 1 ≈ 10.000 * 10 N/m2 (Pa, pour pascals) = 10.000 kgf.
La notion de vide est un corollaire de celle de pression : un volume vide c-à-d ne contenant aucune molécule ni atome implique mécaniquement l'absence de pression dans ce volume. Le vide peut être facilement créé à l'intérieur d'une ventouse en écrasant sa base sur une surface, de sorte que la plupart des molécules d'air en sont éjectées. Par conséquent la pression interne exercée par les quelques molécules éventuellement subsistantes est très inférieur à la pression externe, exercée par la pression atmosphérique. Il en résulte que la ventouse est "collée" contre la paroi.
Pression hydrostatique
On suppose ici une masse de liquide immobile (sans courants). On comprends déjà intuitivement que la pression subie dans un liquide augmente avec la profondeur. Mais qu'en est-il exactement ? Pour répondre à cette question revenons brièvement à la pression atmosphérique. Dans (171) nous avions mentionné la valeur de 10.000 kgf pour la masse totale des particules atmosphériques. Cette masse atmosphérique n'est pas facile à calculer car la densité des particules atmosphériques diminue avec la hauteur.
Pression
hydrostatique
Dans le cas d'un liquide, ses particules sont également sujettes à l'agitation thermique. Mais contrairement aux molécules d'un gaz, qui ne sont pas liées, celles d'un liquide sont liées (de façon semi-rigide, ce qui confère la fluidité de leur ensemble). Ce sont les "ponts hydrogènes" (cas de l'eau), caractérisés par une attraction électromagnétique d'un atome d'hydrogène (H) par un atome d'oxygène (O).
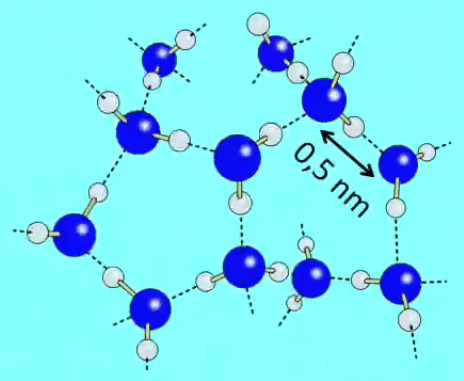
Or ces liens ne dépendent pas des forces extérieures que subissent les molécules (notion de "liquide incompressible", cas de la plupart des liquides) ⇔ la densité, et donc la masse d'un volume déterminé de liquide, varient relativement peu avec la profondeur ⇒ le calcul de la masse d'une colonne de liquide est plus facile que celui d'une colonne de gaz :
par (193) :
M = ρ * V = ρ * h * S où :
• ρ est la masse volumique du liquide ;
• h est la hauteur de la colonne ;
• S est la surface de la base de la colonne ;
⇒ par (170)
P = ρ * h * S * g / S ⇔
P = ρ * g * h
NB : où h est le seul paramètre libre.
NB : (172) n'est pas applicable aux gaz car dans ceux-ci ρ n'est pas constant.
Ainsi pour l'eau, à 10m de profondeur :
P ≈ 1.000 * 10 * 10 = 100.000 [kg / m3 * m / s2 * m = kg * m / s2 / m2= N / m2 = Pa]
Mais attention : pour obtenir la pression totale, il reste à ajouter la colonne atmosphérique située au-dessus de la colonne de liquide ⇒ par (171) : en passant du niveau de la mer à dix mètres de profondeur d'eau on double la pression.
Rappelons que le terme "hydrostatique" est générique, c-à-d utilisé pour tout liquide. Prenons le cas du mercure (Hg), un liquide métallique, dont 1cm3 pèse 13,5g (contre 1g pour l'eau) en raison du grand nombre de protons et neutrons que contient le noyau d'un atome de mercure : 202 contre 18 pour l'eau.
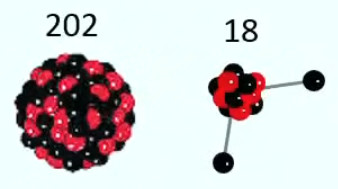
Atome Hg et molécule H2O
NB : 202/18=11,2 est plus petit que 13,5 car le volume de la molécule d'eau est légèrement plus élevé que celui d'un atome de mercure, en raison des deux atomes d'H situés à une certaine distance de l'atome d'O ⇔ la densité d'atomes du mercure est supérieure à celle de l'eau. Ainsi alors qu'avec une colonne de 10m d'eau on obtenait une pression de 100.000 Pa, pour le mercure il suffira de 10/13,5=0,74m.
Principe
de Pascal
Nous allons voir ici que la pression hydrostatique au fond d’un bassin d’eau ne dépend que de la hauteur d’eau et non de la quantité d’eau qui s’y trouve.
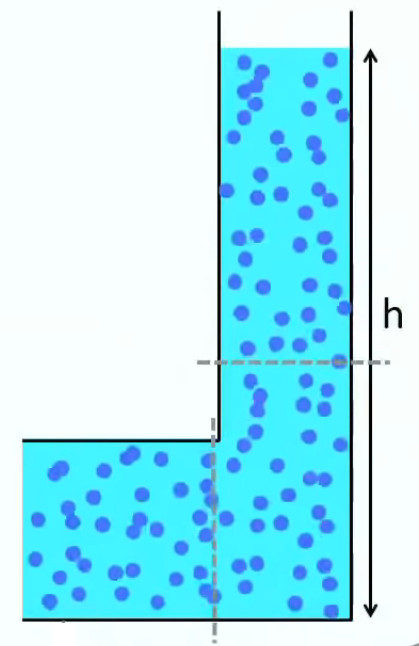
Pour comprendre ce résultat contre-intuitif il faut percevoir la combinaison de deux phénomènes :
- d'une part, l’origine microscopique de la pression : la pression sur une paroi est due aux collisions qu’elle subit de la part des molécules d’eau en mouvement d’agitation thermique. C'est la nature isotrope de la pression, qui explique la répartition uniforme de la pression à une hauteur donnée ;
- d'autre part, la pression exercée par la colonne sur sa base augmente avec la hauteur de la colonne. Mais à une hauteur déterminée, la pression est identique quelle que soit la largeur de la colonne, et donc quelle que soit la surface de sa base : ainsi dans le développement de (172) on voit bien que le facteur de surface S disparaît par la substitution de :
M = ρ * V = ρ * h * S
dans :
P = M * g / S = ρ * h * S * g / S ⇔
P = ρ * g * h (172)
La combinaison de ces deux phénomènes a pour effet que diminuer la largeur de la colonne du graphique ci-dessus ne changera rien à la pression en n'importe quel point de la base du bassin. Ce résultat constitue le principe de Pascal.

Crève-
tonneau
L'expérience du "crève-tonneau" est particulièrement parlante : avec une quantité d'eau ridiculement faible il est possible de crever un tonneau de bois. On voit que l'eau injectée dans la colonne joue comme un piston qui pousse sur la surface de l'eau. Le principe de Pascal permet ainsi d'expliquer le principe des vases communicants, ainsi que le principe du siphon.
Vases
communicants
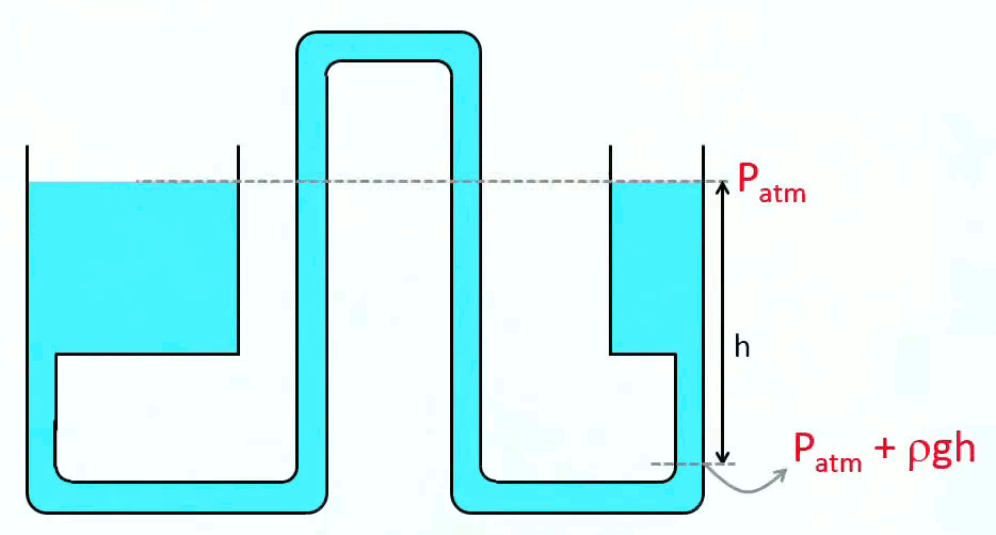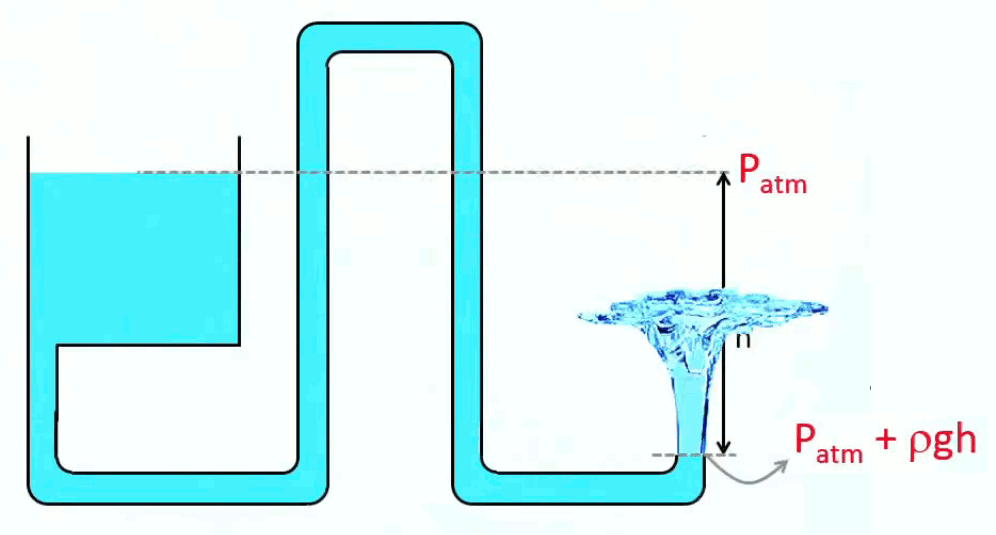
Le schéma suivant illustre deux vases communiquant par un tuyau. la vanne rouge est alors fermée, et puis du liquide est rajouté dans le vase de droite ⇒ la hauteur de la colonne augmente ⇒ la pression augmente dans la partie droite du système ⇒ si on ouvre la vanne rouge, la pression se propage dans la partie gauche, dont le niveau va monter jusqu'à ce que les hauteurs dans les deux vases soient au même niveau (qui sera évidemment plus élevé que le précédent niveau d'équilibre).
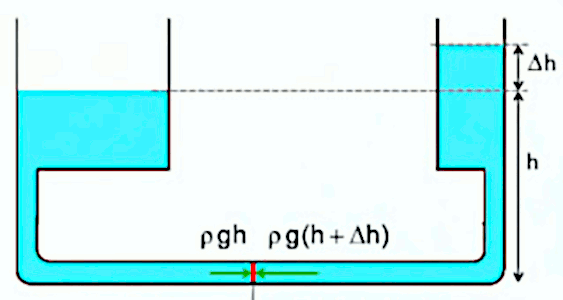
Le système illustré ci-dessous permet d'affiner notre compréhension du phénomène : que vaut la pression Px dans la partie la plus haute du tuyau ? On sait que :
- au niveau de la ligne hachurée la pression est partout la pression atmosphérique ;
- dans la partie haute du tuyau la pression Px est moins forte qu'au niveau de la ligne hachuré puisque cette partie haute ne subit pas la pression de la colonne h1
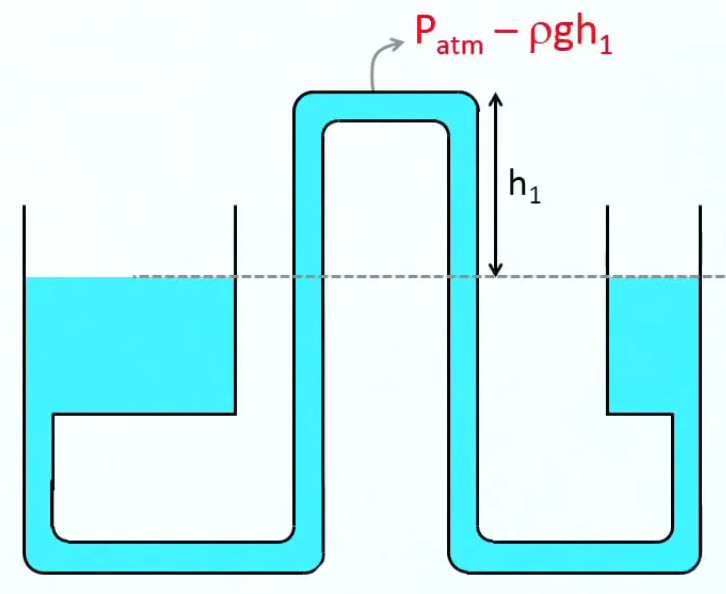
Par conséquent : Px = Patm - ρ * g * h1
Syphon
Si dans le graphique précédent on retire à droite une partie de la colonne à partir de là où la pression vaut Patm + ρ * g * h ⇒ la pression juste au dessus de la section ne sera plus égale qu'à Patm, et ne pourra donc contenir la pression Patm + ρ * g * h provenant d'en-dessous la section. On pourra ainsi vider le vase de gauche, par siphonnage.
Le principe d'Archimède est expliqué ici sans référence au calcul des pressions subies par les parois rigides d'un volume d'eau immergé (qui sont supérieures sur la partie inférieure que sur la partie supérieure).
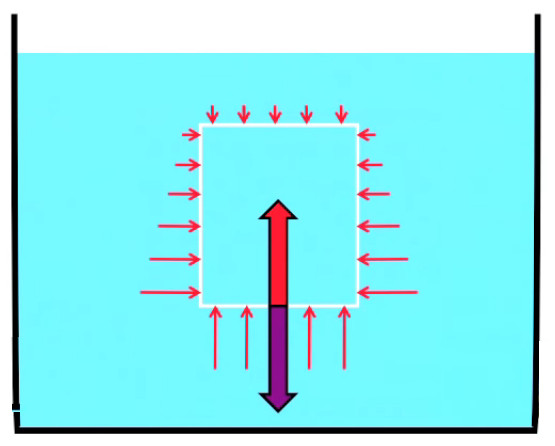
On peut néanmoins comprendre que ce volume est soutenu par la masse d'eau qui l'environne, par le jeu de ces pressions sur toute la surface du volume.
Si ce même volume est rempli de béton plutôt que de l'eau, alors il va s'enfoncer car son poids volumique est supérieur à celui de l'eau. Si au contraire le volume est remplis de bois, il va s'élever car le poids volumique du bois est inférieur à celui de l'eau. Une question qui vient alors à l'esprit est de savoir ce qui détermine la répartition entre volume immergé et volume émergé du volume total de bois flottant à la surface.
Le principe d'Archimède stipule que « tout corps plongé dans un fluide au repos, entièrement ou partiellement, subit une force dirigée de bas en haut, et opposée au poids du volume de fluide déplacé. Cette force appelée poussée d'Archimède s'applique au centre de masse du fluide déplacé ». Autrement dit, un corps qui flotte est tel que son poids (force gravitationnelle vers le bas) est égal à la poussée exercée vers le haut par le volume de liquide qu'il déplace.
Ainsi dans la partie droite de l'image suivante la partie immergée du bloc de poids est telle que son poids en eau est égal au poids total du bloc de bois ⇔ le volume de bois immergé est le même que le volume d'eau dont le poids vaut celui du bloc de bois.
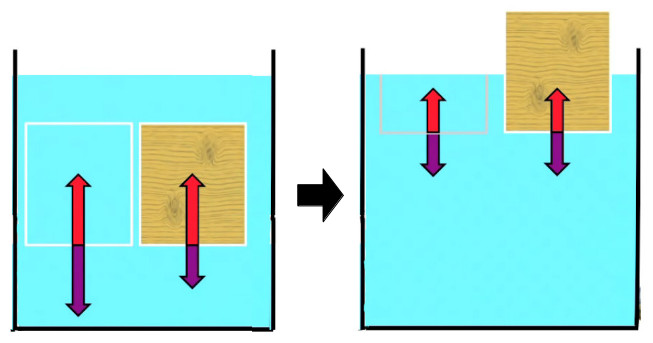
Gauche : le bloc de bois monte. Droite : il est à l'équilibre.
On comprends alors qu'il peut exister des bateaux en acier ou en béton : le volume ne contient ces matériaux qu'au niveau des parois, de sorte que le poids de l'ensemble de la structure flottante peut être égal au poids du volume en eau de la partie immergée. Dans ce cas la structure flotte.
Force et énergie
2. Rotation
3. Énergie cinétique
Travail
Tout travail réalisé (par un organisme vivant ou une machine) requiert de l'énergie. Toutes les formes que peut prendre l'énergie résultent de l'action de force et de déplacements.
N.d.A. Travail et énergie sont égaux en quantité, mais se différencient par leur nature : le travail est une action, tandis que l'énergie est un potentiel d'action. C'est par l'action du travail qu'une quantité d'énergie peut être transformée en une quantité égale d'une énergie d'un autre type.
Cela est évident pour laver le linge (à la main ou en machine) ou encore pétrir de la pâte (à la main ou par une machine). Nous allons montrer ici la combinaison force+déplacement dans des cas où la force et le déplacement sont à priori moins apparents.
Commençons par le cas du fil de cuivre, composé d'un ensemble d'atomes de cuivre. Ceux-ci ont pour caractéristique, lorsqu'ils sont à proximité les uns des autres de libérer des électrons. Un courant d'électrons peut ainsi être créé. Chacun de ces électrons qui entre en collisions avec un atome de cuivre, met celui-ci en vibration, laquelle se communique aux autres atomes de cuivre, de proche en proche. Cette agitation se manifeste par de la chaleur : on parle d'énergie calorifique. Le courant électrique créé de l'énergie calorifique, mais il faut préalablement de l'énergie pour créer le courant électrique.
Pour ce faire un générateur (de centrale électrique ou d'éolienne) consiste à exploiter la force de Lorenz (64) dans un système composé d'une bobine de fil de cuivre qui à l'aide d'un rotor est mise en mouvement dans un champ magnétique.

Un autre exemple pour illustrer l'énergie comme la combinaison d'une force et d'un mouvement est l'énergie électromagnétique. Ainsi une antenne est un fil de cuivre le long duquel les électrons se déplacent en aller-retours sous l'action de sources de tensions variables, et ce faisant provoquent une onde électrique qui va se propager puis être détectée par une antenne.

Flèche rouge : force électrique ⇒ flèche bleu déplacement des électrons
L'onde du champ électromagnétique n'est rien d'autre qu'un transport d'énergie, comme en témoignent les électrons dans le circuit de l'antenne réceptrice (originellement sans sources de tension), qui vont ainsi se mettre à de déplacer eux-aussi dans un mouvement de va-et-viens le long de l'antenne.
Les mêmes principes valent pour la lumière. Dans le filament de l'ampoule on observe des vibrations extrêmement rapides des électrons. Ces vibrations génèrent elles aussi des ondes électromagnétiques. Celles-ci peuvent être détectées par des récepteurs de l'oeil, sensibles à la force électrique portée par l'onde électromagnétique lumineuse.
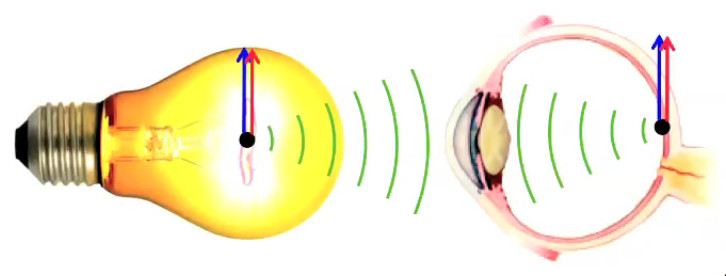
Un dernier exemple est donné par l'énergie nucléaire qui vient des noyaux atomiques, composés de neutrons (charges 0) et protons. Ces derniers étant tous de chargent +, ils se repoussent d'autant plus fort qu'ils sont extrêmement compactés. Dans les noyaux de grande taille, tels que ceux de l'uranium ou du plutonium, cela peut aller jusqu'à l'éclatement de l'atome, libérant ainsi une énergie considérable.
Réaliser un travail (noté W) est la forme la plus élémentaire d'énergie : cela consiste à exercer une force F sur une longueur L :
W = F * L [W = N * m = J (joule)]
L est généralement noté x(t) lorsqu'on souhaite exprimer la distance parcourue en fonction du temps.
On peut démontrer (173) par un double expérience de pensée. Soit W0 un travail de référence consistant à élever une masse M à une hauteur L ⇒ :
- si j'élève cette masse à une hauteur 2*L ⇒ je réalise un travail W=2*W0 ⇒ W∝L ;
- si j'élève une masse 2*M à une hauteur L ⇒ je réalise un travail W=2*W0 ⇒ W∝F ;
Leviers. Le principe du levier – qui permet de démultiplier une force – est une illustration très intuitive des notions de travail et de conservation de l'énergie.
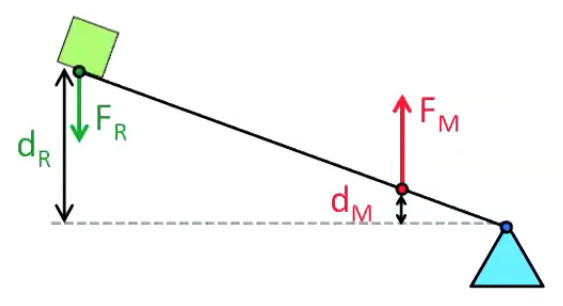
Le levier est un système mécanique caractérisé par trois points (cf. graphique infra) :
- point d'appui du levier ;
- point d'application de la force motrice FM sur le levier, à laquelle correspond la longueur du bras de levier moteur LM (toujours mesurée par rapport au point d'appui du levier) ;
- point d'application de la force résistante FR (là où se situe la masse) sur le levier, à laquelle correspond la longueur du bras de levier moteur LR (toujours mesurée par rapport au point d'appui du levier).
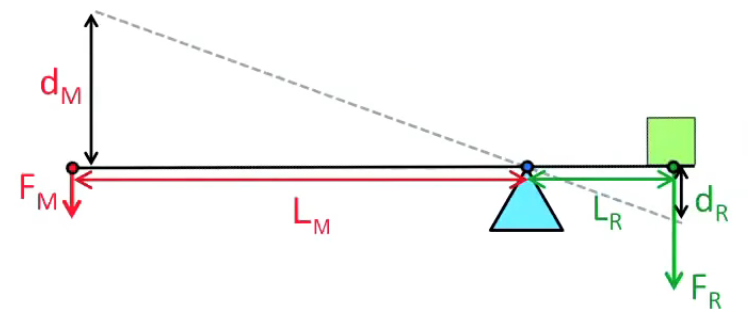
Levier de type "inter-appui"
Aux points d'application de FM et de FR correspondent les distances LM et LR, toutes deux mesurées par rapport au point d'appui.
On distingue divers types de levier, les plus simples étant :
- inter-appui : le point central est le point d'appui (graphique ci-dessus) ;
- inter-résistant : le point central est le point de résistance (cas de la brouette) ;
- inter-moteur : le point central est le point moteur (cas du bras) ;
Les deux systèmes sont identiques dans leurs situations extrêmes LR=0 et LM=0
La loi (d'équilibre) des leviers :
FM * LM = FR * LR
s'écrit plus simplement en l'exprimant comme l'égalité des moments de force (cf. infra #moment-force) :
τM = - τR
Une autre relation lie FM et FR via la force du point d'appui FA : FM + FA = FR. Mais elle ne joue pas car le bras de levier correspondant LA ≡ 0 par définition ⇒ τA ≡ 0 par définition.
Démonstration :
pour démontrer la loi des levier il faut introduire la notion de conservation de l'énergie : quelle que soit la nature (méthode) du travail effectué pour déplacer une masse M sur une distance L – par exemple un palan (cf. section suivante) plutôt qu'un levier – l'énergie impliquée sera toujours la même. En l'occurrence il s'agit de démontrer l'égalité entre d'une part le travail associé au déplacement dM du point d'application de la force motrice FM, et d'autre part le travail associé au déplacement correspondant dR du point d'application de la force résistante FR :
WM = WR ⇒
FM * dM = FR * dR
D'autre part on peut établir géométriquement la valeur du facteur de démultiplication (r) en constatant dans l'image supra la constance du rapport :
dM / LM = dR / LR
(cf. les deux triangles axés sur le point d'appui du levier) ⇔
dM / dR = LM / LR = r
qu'il suffit alors de substituer dans (175) ⇒
FM * LM = FR * LR
CQFD.
Il résulte de (174) et (176) que :
FM = FR / r
Les deux images suivantes illustrent le levier inter-moteur (cas des leviers du corps humain). Dans le cas du bras le facteur de démultiplication r = LM / LR = 1/7 < 1 ⇒ par (177) : FM = 7 * FR: pour soulever un poids de 1kgf je dois exercer une force de 7 kgf. Faut-il en déduire que le corps est une machine bien peu efficace ? Pas du tout, car la force importante qu'il faut exercer est compensée par (c-à-d "est le prix à payer pour") un long bras de levier résistant, c-à-d pour une grande amplitude de mouvement, ce qui pour un organisme vivant est une propriété qui peut s'avérer vitale (pour fabriquer des outils, ou encore se déplacer dans les branches d'un arbre).
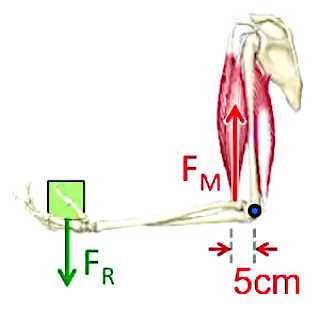
Le bras est un levier de type "inter-moteur".
Levier de type "inter-moteur" schématisé.
N.d.A. En comparant le levier au palan (système de levier à poulie) on constate que le progrès technologique ne peut faire autre chose que de rendre possible des combinaisons différentes de F et L pour une même quantité d'énergie/travail.
Le principe du palan est proche de celui du levier :
- on y retrouve les notions de force moteur et force résistante ;
- une corde remplace le levier
- la poulie joue un rôle de point d'appui.
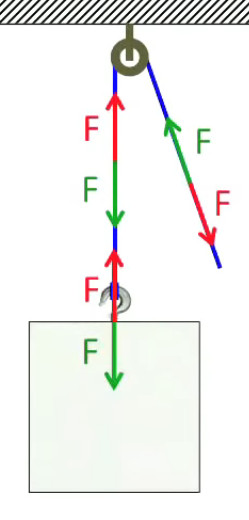
Une notion supplémentaire est introduite : la force de tension, qui est répartie sur toute la longueur de la corde, entre le point d'action de la force résistante et celui de la force moteur.
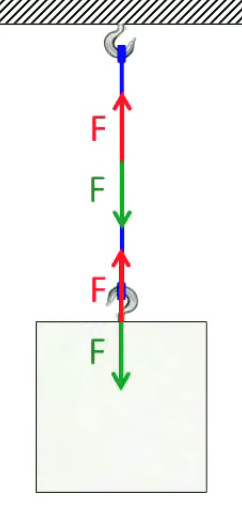
Le schéma suivant est l'illustration la plus simple de la force de tension : chaque point de la corde subit une force égale vers le haut et vers le bas (concrètement, les fibres de la corde, ou les maillons d'une chaînes, sont étirées dans les deux sens ⇒ la notion de "tension de rupture", fonction du matériau). C'est en réalité une version simplifiée de la poulie, où le point d'application de la force moteur est située au niveau du crochet supérieur.
Le palan est donc un système plus sophistiqué que le levier car il permet d'orienter la direction de la force moteur (quant à sa roue, elle a pour fonction de réduire les forces de frottement à un niveau minimum).
Dans ce système la force moteur à exercer pour soulever la masse est égale à son poids. On n'a donc pas encore d'effet de démultiplication permis par le système du levier. Nous allons montrer progressivement que pour cela il faut fixer la poulie sur la masse !
Commençons par montrer que le principe de démultiplication du palan repose sur le fait que si le point d'action de la force moteur est fixée sur la masse elle-même (donc par un second crochet), il en résulte que la force de tension est répartie sur les deux segments de corde, c-à-d qu'elle vaut F/2 en tout point ! Or rien n'empêche d'inverser le système : crochets en haut et poulie en bas.
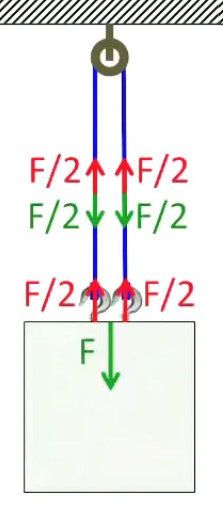
Ensuite si l'on remplace un des deux crochets du haut par un point d'application libre de la force moteur, la force à exercer pour soulever un poids est divisée par deux. Cependant il y a un "prix à payer". Pour le montrer abaissons le point d'application de la force moteur jusqu'à la poulie ⇒ toute la longueur L de la corde est sur l'autre côté ⇒ si je remonte le point d'application de la force moteur jusqu'en haut (c-à-d sur une hauteur L), la masse ne montera nécessairement que de la moitié de cette hauteur maximale.
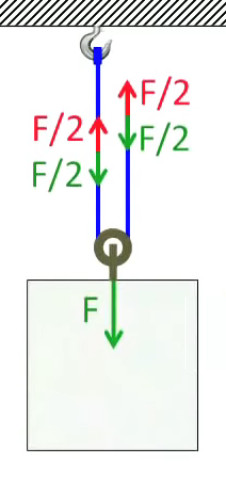
Ce prix à payer est l'illustration du principe de conservation de l'énergie : l'énergie ne se perd ni ne se créé, mais se transforme. Étant donné que l'énergie, c-à-d le travail, égale le produit de la force et de la distance :
- si le travail pour élever de L/2 la masse, sans palan, vaut : W = F * L/2
- alors le travail pour élever de L/2 la masse, avec ce palan, vaut : W = F/2 * L
Ainsi avec le système du palan, une personne de force insuffisante pourra néanmoins arriver à soulever la masse si elle est suffisamment endurante.
On peut améliorer le système du palan, c-à-d obtenir des rapports supérieurs à 2 en augmentant le nombre de poulies. Mais combien, et comment ? En ajoutant une poulie en haut on peut alors tirer vers le bas (ce qui est pratique), mais sans augmentation de la démultiplication, puisque le nombre de segments soutenant la charge n'a pas augmenté. Pour cela il faut ajouter une seconde poulie sur la masse ! Et dans ce cas puisque la tension est répartie sur quatre cordes, la force requise est divisée par 4, .... mais le point d'application de la force résistante se déplace quatre fois moins que le point d'application de la force moteur.
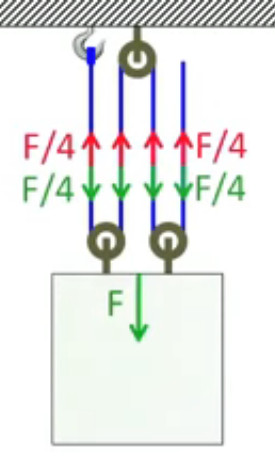
Pour le montrer abaissons le point d'application de la force moteur jusqu'à la poulie ⇒ toute la longueur L de la corde est répartie sur les trois autres segments ⇒ si je remonte le point d'application de la force moteur jusqu'en haut, c-à-d, de L/3, la masse ne montera nécessairement que de L/3 à L/4 c-à-d de L/3-L/4=L/12 ⇒ :
- si le travail pour élever de L/12 la masse, sans palan, vaut : W = F * L/12
- alors le travail pour élever de L/12 la masse, avec ce palan, vaut : W = F/4 * L/3
Nous avons vu jusqu'ici trois cas : un, deux et quatre segments porteurs ⇒ le cas avec trois segments porteur se déduit facilement : la règle pour déterminer le nombre de segments porteurs est double :
- on ne compte que les crochet et poulie(s) placés sur la masse ;
- crochet=1 ; poulie=2.
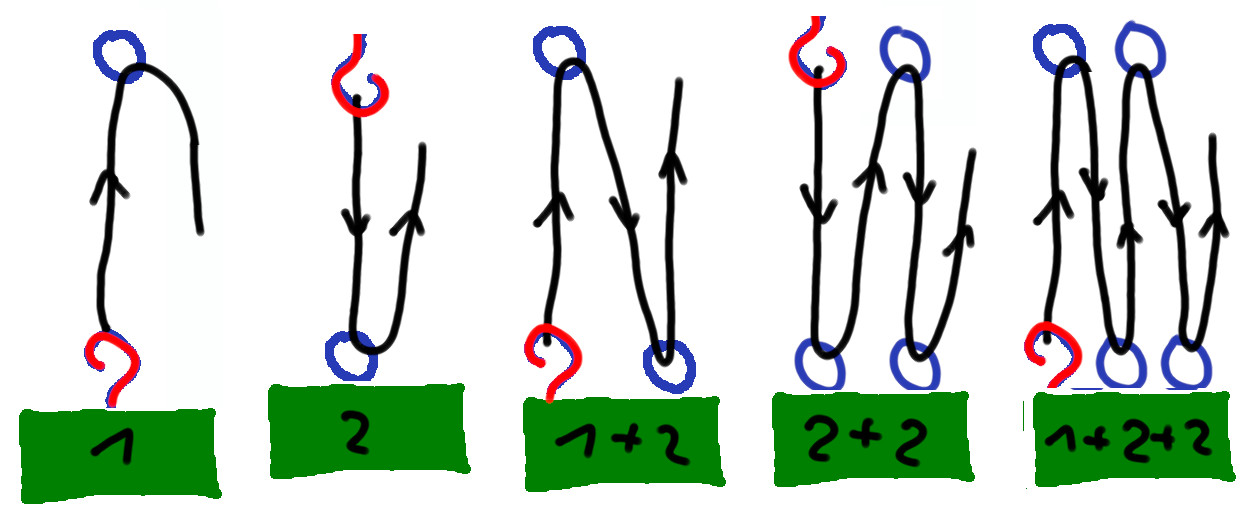
N.B. Alternance haut/bas du crochet ⇒ :
• crochet en bas ⇒ # impair de segments porteurs ;
• crochet en haut ⇒ # pair de segments porteurs.
Pour trois segments porteur le raisonnement est évidemment toujours le même. On abaisse le point d'application de la force moteur jusqu'à la poulie ⇒ toute la longueur L de la corde est répartie sur les deux autres segments ⇒ si je remonte le point d'application de la force moteur jusqu'en haut, c-à-d sur une hauteur de L/2, la masse ne montera nécessairement que de L/2 à L/3 c-à-d de L/2-L/3=L/6 ⇒ :
- si le travail pour élever de L/6 la masse, sans palan, vaut : W = F * L/6
- alors le travail pour élever de L/6 la masse, avec ce palan, vaut : W = F/3 * L/2
Rotation
Moment
de force
Nous avions déjà évoqué la notion de moment de force pour illustrer celle de #produit-vectoriel. Nous allons ici approfondir la notion de moment de force au regard de ce que nous avons appris entre-temps concernant la loi d'équilibre des leviers FM * LM = FR * LR ⇔ τM = - τR (174) (où la lettre grecque "Tau" exprime la torsion). Le principe est ici qu'un même moment de force peut correspondre à différentes combinaisons (F,L).
On appelle équilibre de rotation l'égalité τM + τR = 0. Il est facile de démontrer de τR peut être décomposée en une somme de moments de force correspondant chacun à un couple (Fi,Li) ⇒ τM + ∑in τRi = 0. Le moment de force est ainsi clairement une grandeur additive.
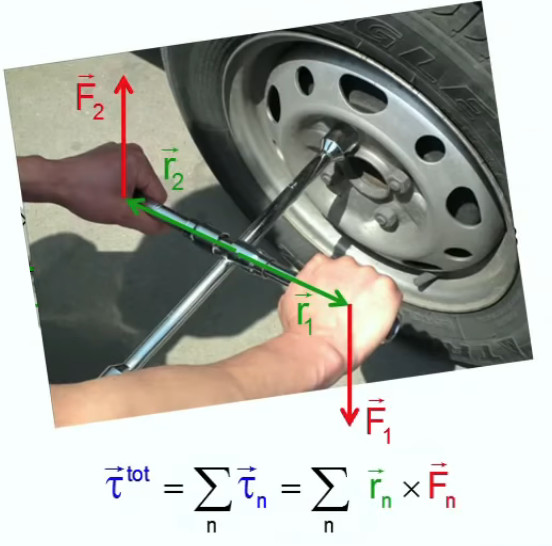
Nous allons maintenant passer à la notation vectorielle du moment de force. Pour ce faire on commence par simplement changer la notation τ = F * L, où L représente la longueur du bras de levier, par τ = F * r où r représente le rayon de courbure de la trajectoire suivie par le point d'application de la force.
L'angle que fait cette force avec la direction du rayon peut-être quelconque, pourvu qu'on la prenne en compte. Intuitivement on comprend que la force est maximale lorsque cet angle vaut π/2 (force tangente à la courbure), et nulle lorsqu'elle vaut π (force dans le même axe que le rayon de courbure).
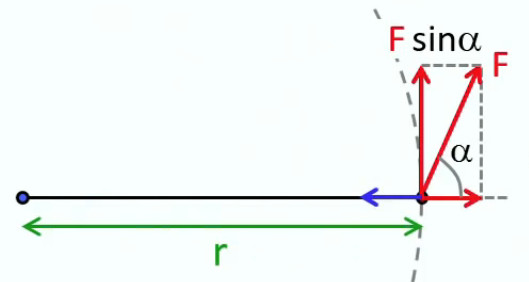
Par conséquent, dans le cas d'un angle située entre les deux, seule la composante perpendiculaire aura un effet sur le moment de rotation ⇒ :
τ = r * F * sinα ⇔
où α est donc l'angle entre la force F et le bras de levier r→, celui-ci étant le vecteur position du point d'application de la force, l'origine de ce vecteur position étant l'axe de rotation des vecteurs.
τ→ = r→ x F→
La règle de la main droite vue à la suite de (62) s'applique donc : le moment de force τ→ est le vecteur perpendiculaire au plan formé par les vecteurs r→ et F→, le sens positif de τ→ étant alors indiqué par la direction du pouce. L'image ci-contre illustre la propriété de translation des vecteurs, en l'occurrence celui du vecteur force déplacé à l'origine pour illustrer clairement l'application de la règle de la main droite : le signe "pointe de flèche" ⊙ montre que le vecteur τ→ sort bien du plan de l'écran.

Unité. NB : bien que l'unité du moment de force est N*m on ne peut pas pour autant en déduire qu'il s'agit de joules : le moment, c-à-d une force exercée sur un bras de levier, n'est pas une énergie.
Moment
d'inertie
Pour illustrer le mouvement de rotation on prend le cas du pendule, mais en faisant abstraction de la force de gravitation : on peut donc le considérer dans un plan horizontal. Et étant donné la construction du système de pendule, la force centrifuge exercée par la masse sur la tige du pendule est compensée par la force centripète (en raison de la rigidité du câble). Le même principe vaut pour la composante de la force dans le sens du pendule.
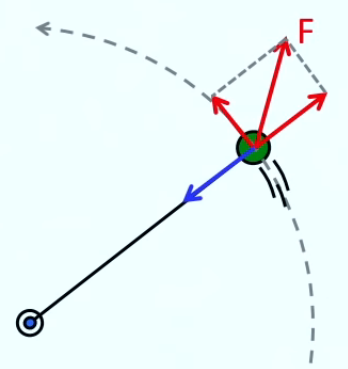
Il ne reste donc que la composante de force perpendiculaire à la tige du pendule ⇒ on peut décrire ce mouvement circulaire comme s'il était rectiligne ⇒ on peut appliquer la loi de Newton :
Étape 1.
m * a = F ⇔ par (31) :
m * a = F * sin(α) ⇔
m * d2x / dt2 = F * sin(α)
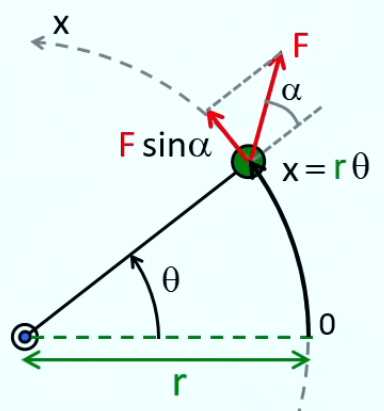
Pour modéliser le mouvement de rotation on ne va pas utiliser la coordonnée de position x mais la coordonnée angulaire θ. Pour ce faire on passe de x à θ (en radians) par :
x = r * θ (1) ⇒
d2x / dt2 = r * d2θ / dt2 ⇒
m * r * d2θ / dt2 = F * sin(α) ⇔
d2θ / dt2 = F * sin(α) / ( m * r ) ⇒
dθ / dt = F * sin(α) / ( m * r ) * t ⇒
θ = F * sin(α) / ( m * r ) * t 2 / 2
c-à-d l'équivalent angulaire de xt = x0 + v0 * t + a * t2 / 2 (164) où position et vitesse initiales sont nulles.
NB : l'accélération angulaire d2θ / dt2 = F * sin(α) / ( m * r ) est donc au mouvement de rotation ce que l'accélération rectiligne a est au MRUA.
Étape 2. Passons maintenant à un cas plus général, tel que le point d'application de la force extérieure n'est pas nécessairement situé sur la masse (cf. graphique suivant).
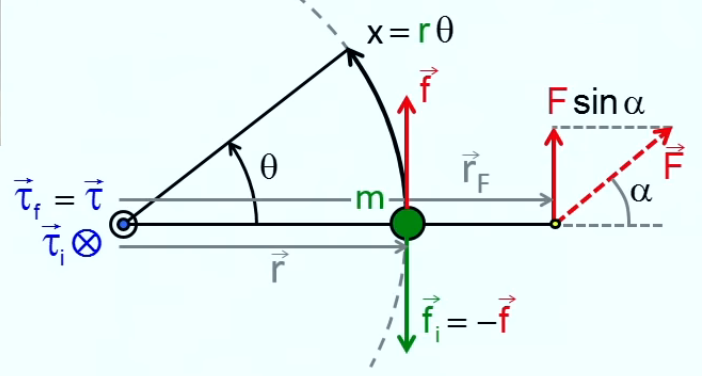
En fait il s'agit d'un système de levier, et on peut donc lui appliquer la loi des leviers (174) :
r * fi = rF * F * sin(α) ⇔
fi = rF / r * F * sin(α) ⇒
en vertu de la notion d'équilibre dynamique, c-à-d le fait que les forces apparaissent toujours par couple de forces opposées (169) :
f = rF / r * F * sin(α)
On refait alors comme précédemment :
m * a = f ⇔
m * d2x / dt2 = rF / r * F * sin(α) ⇔
m * r * d2θ / dt2 = rF / r * F * sin(α) ⇔
NB : on retrouve bien le cas précédent (force appliquée sur la masse) en posant rF = r.
• d2θ / dt2 = rF * F * sin(α) / ( m * r2 ) ⇔
• θ(t) = 1/2 * rF * F * sin(α) / ( m * r2 ) * t2
⇔ par (179) :
• d2θ / dt2 = τ / ( m * r2 ) ⇔
• θ(t) = 1/2 * τ / ( m * r2 ) * t2
Le carré du rayon exprime une forte sensibilité à la distance.
Si on passe de la notation scalaire à la notation vectorielle pour appliquer la règle de la main droite, on observe dans l'image supra que ses résultats (symboles ⊗ et ⊙ au point pivot) sont cohérents avec l'égalité des moments de force (au signe près) :
τ→i = r→ x f→i = r→ x - f→ = - τ→f ⇒
par supra :
r * f = rF * F * sin(α) ⇒
- τ→i = τ→ ⇔
τ→i + τ↔ = 0
Étape 3. Passons maintenant à un cas encore plus général en supposant le cas de deux masses distinctes du point d'application de la force extérieure.
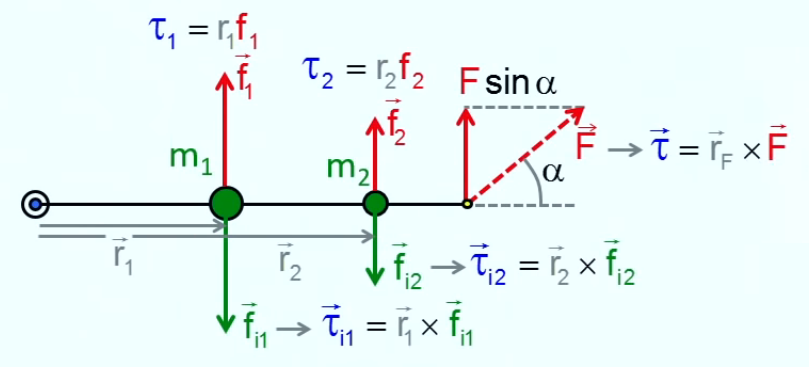
Pour ce faire on va à nouveau recourir à la notion d'équilibre dynamique exprimée en fonction des moments de force :
τ→i1 + τ→i2 + τ↔ = 0
c-à-d que le moment de force extérieur compense les moment de force d'inertie combinés. Et selon ce même principe d'équilibre dynamique les forces d'inertie sont compensées par les forces qui accélèrent les masses, via la structure rigide du pendule c-à-d via leurs moments de force respectifs :
τ→i1 = - τ→1 et τ→i2 = - τ→2
que l'on substitue dans l'égalité précédente ⇒
τ→1 + τ→2 = τ↔
⇒ on passe à la notation scalaire, ce qui simplifiera le développement :
τ1 + τ2 = τ
où l'on injecte les valeurs de τ données par le résultat de l'étape 2 ⇒
m1 * r12 d2θ / dt2 + m2 * r22 d2θ / dt2 = τ ⇔
( m1 * r12 + m2 * r22 ) * d2θ / dt2 = τ
• où J = m1 * r12 + m2 * r22 est le "moment d'inertie"
• où l'on retrouve le résultat de l'étape 2 en posant r1=r2 et m1+m2=m
Le tableau suivant permet de comparer la loi de Newton et sa version adaptée au mouvement circulaire.
| Rectiligne | m * d2x / dt2 = f |
|---|---|
| Rotation | ( m1 * r12 + m2 * r22 ) * d2θ / dt2 = τ |
Généralisation finale :
l'équation du mouvement de rotation vaut pour un nombre indéfini de masses, dont le moment d'inertie vaut : J = ∑n=1N mn * rn2
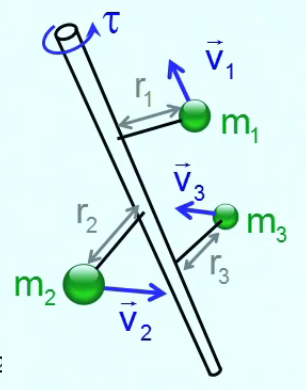
l'équation du mouvement de rotation vaut également pour une localisation indéfinie dans l'espace à trois dimensions (du système du levier) car toute localisation en dehors de l'axe contenant le point d'application de la force extérieure peut y être ramené par rotation et translation ; NB : la distance r se calcule par rapport à la distance à l'axe de rotation.
En pratique pour calculer le moment d'inertie d'un corps en trois dimension on va "décomposer" celui-ci en un nombre arbitrairement élevé de cubes élémentaires ΔVn (donc de taille arbitrairement petite), chacun étant caractérisé par une distance rn par rapport à l'axe de rotation. Quant à la masse de chacun de ces volumes élémentaires on l'obtient par la masse volumique ρ : mn = ρ * ΔVn (193) ⇒
J = ∑n=1N ρ * ΔVn * rn2 ⇒
J = ∫n=1N ρ * dVn* rn2
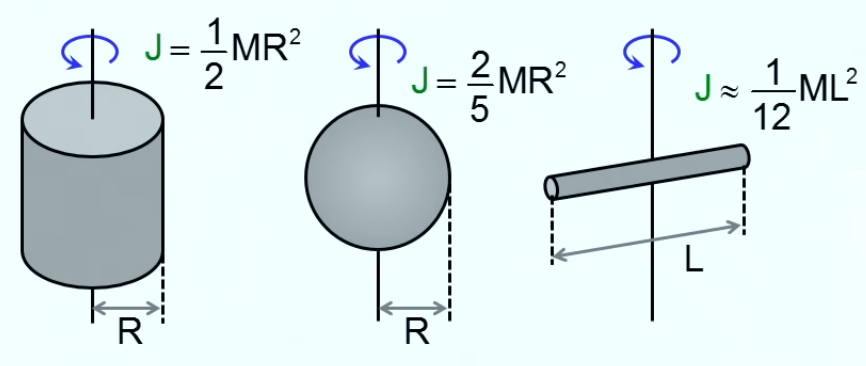
On peut montrer que l'on obtient des formules assez simples pour le moment d'inertie des volumes suivants :
Énergie cinétique
Conservation et
transformation
Le travail est une forme d'énergie. En poussant sur un mur de légos, je peux le faire tomber grâce au travail des mes muscles. Par le travail de mes muscles je peux également envoyer une balle sur ce mur, ce qui aura le même effet. Pourtant la balle ne dispose d'aucun muscle ou mécanisme artificiel lui permettant d'effectuer un travail. L'explication est que le travail effectué pour lancer la balle s'est transformé en énergie (en l'occurrence cinétique), transféré dans la balle par mon travail musculaire. Ensuite, lors du choc de la balle avec le mur, c-à-d lorsque la balle a exercé une force sur le mur, la balle a transféré de l'énergie cinétique au mur, et sa valeur vaut le produit de la force d'inerte par la longueur du déplacement du mur.
Il convient donc de distinguer dans cette chaîne :
- la force mécanique appliquée par les muscles pour conférer à la balle une énergie cinétique : W = = Fmeca. * L = Ec
- la force d'inertie exercée ensuite par la balle sur le mur, et par laquelle l'énergie cinétique va être transformée en travail : Ec = Finer. * L = W.
N.d.A. La quantité d'énergie cinétique transférée peut varier en fonction notamment des forces de frottement qui ont été impliquées dans chacun des modes de transfert/transformation de cette chaîne. Ces forces de frottement sont transformées (on dit qu'elles se "dissipent") en chaleur (au niveau des muscles, puis du mur, ...) c-à-d en énergie calorifique.
Énergie
potentielle
Si plutôt que de lancer horizontalement une masse, je la lève pour la poser sur un support d'une certaine hauteur, la masse s'y trouvera au repos. Le travail mécanique que j'ai réalisé ne s'est donc pas transformée en énergie cinétique. Mais en vertu du principe de conservation, le travail fourni s'est nécessairement transformé en une forme d'énergie. Celle-ci est appelée "énergie potentielle". Pour observer physiquement son existence, faisons disparaître le support par expérience de pensée ⇒ la masse tombe, et laisse sur le sol une empreinte qui n'existait pas, et la profondeur de cette empreinte sera d'autant plus grande que la masse aura été préalablement élevée à une grande hauteur.
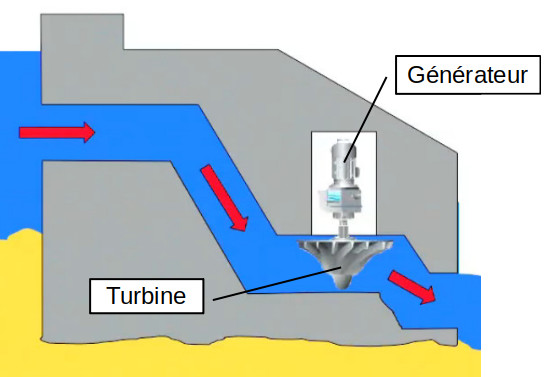
Le fonctionnement des barrages hydroélectriques est fondé sur le principe de l'énergie potentielle : lorsque les vannes sont ouvertes l'énergie potentielle de l'eau qui descend dans le conduit se transforme en énergie cinétique par la force du courant ⇒ celle-ci pousse les aubes de la turbine située plus bas, de sorte que l'énergie cinétique de l'eau est ainsi transformée en énergie électrique via le générateur (N.d.A. : du moins partiellement car une partie de l'énergie cinétique est dissipée en énergie calorifique par les forces de frottement inhérentes au mécanisme de la turbine).
On observe également l'énergie potentielle au niveau atomique. Ainsi la pile électrique exploite la force électrique qui attire un électron et un proton [cf. infra #atomes et #cohesion-electromagnetique] : des protons (signe +) ont été placés d'un côté, et des électrons (signe -) de l'autre ⇒ si l'on place un fil conducteur entre les deux "bornes" on créé un courant de charges électriques (dans le sens - vers +), qui peut alors alimenter un appareil électrique (lampe de poche, ventilateur, ...).
De même l'élasticité de certaines molécules permet d'y stocker de l'énergie potentielle en les maintenant dans un état de tension ou de pression.Nous verrons dans la section #potentiel-gravitationnel une formulation mathématique de l'énergie potentielle.
Énergie
cinétique
Il suffit de lâcher une masse sur un sol meuble, à plusieurs hauteurs différentes pour constater que l'énergie cinétique augmente avec la masse et la vitesse : Ec = f( m, v ), qui exprime que l'énergie cinétique est l'énergie "enfermée" dans le mouvement d'une masse. Mais quelle est la formule exacte de la fonction f() ? Pour trouver la réponse à cette question il suffit d'exprimer W=Ec en fonction de m et de v ⇒
dans :
W = F * x(t) (173)
on substitue :
F = m * a (168) ⇒
W = m * a * x(t)
où l'on substitue
a = v(t) / t (163)
x(t) = v(t) * t / 2 (165)
⇒
W = m * v(t) / t * v(t) * t / 2 ⇔
W = m * v(t)2 / 2
À partir de cette équation, que se passe-t-il lorsqu'au temps t la force de propulsion devient brusquement nulle, c-à-d lorsque plus aucun travail n'est fourni ? Dans ce cas l'énergie cinétique n'augmente plus ⇒ la vitesse est donc constante (NB : on fait toujours abstraction des forces de frottement) ⇒ on est revenu en MRU ⇒ on peut donc simplifier l'équation en supprimant la référence au temps :
Ec = m * v2 / 2 [kg*(m/s)2=J]
Ainsi l'énergie cinétique d'une voiture de 600 kg se déplaçant à 106 km/h=106*1000/3.600 m/s ≈ 29 m/s vaut :
Ec = 600 * 302 / 2 = 270.000 J = 270 kJ soit environ trois fois moins que l'énergie contenue dans un petit pot de yaourt. C'est l'énergie qu'il faut dépenser pour pousser une voiture de 600kg jusqu'à ce qu'elle atteigne (NB : sans forces de frottement) une vitesse de 106 km/h.
N.d.A. L'équation (185) correspond à une réalité physique : celle des planètes qui dans le vide ne sont pas soumises à des forces de frottement.
Référentiel. Mais pour utiliser cette équation correctement il faut bien spécifier le référentiel par rapport auquel elle est appliquée. On peut ainsi considérer que la voiture est à l'arrêt dans son référentiel (v=0 ⇒ Ec=0), et que c'est le référentiel de la Terre qui défile en-dessous de ses roues, en vertu du principe de relativité des référentiels inertiels (cf. supra #relativite). Comprenons donc bien que la notion d'énergie cinétique n'est pas absolue, mais relative à un référentiel. Elle est d'ailleurs essentiellement utilisée pour faire des bilans énergétiques c-à-d la différence entre deux mesures avant et après un événement physique.
Énergie
de rotation
Lorsque nous avons étudié le moment d'inertie (cf. supra #moment-inertie) nous avons vu que seule la composante de force perpendiculaire à la tige du pendule devait être prise en compte et que par conséquent on peut décrire ce mouvement circulaire comme s'il était rectiligne, en appliquant la loi de Newton F = m * a (168). Mais nous avons vu aussi qu'il était utile de remplacer les coordonnées de position x par la coordonnée angulaire θ. Nous allons donc faire de même pour l'énergie cinétique Ec = m * v2 / 2 (185) :
soit l'arc-radian :
x = r * θ (1) ⇒
v = dx / dt = r * dθ / dt ⇒
on appelle vitesse angulaire :
ω = dθ / dt = 2 * π / T
où T est la période du mouvement c-à-d le temps mis pour faire un tour,
⇒ v = r * ω
que l'on substitue dans (185) ⇒
Ec = m * r2 * ω2 / 2 ⇔ par (183) :
Ec = J * ω2 / 2 ⇔
Le tableau suivant compare les formules de l'énergie cinétique selon le type de mouvement.
| Rectiligne | Ec = m * v2 / 2 |
|---|---|
| Rotation | Ec = J * ω2 / 2 |
Application. On prend le cas d'un moteur monocylindre, dont le mouvement du cylindre est en quatre temps : explosion (qui produit de l'énergie) plus trois phases (échappement ⇒ admission ⇒ compression), qui ne produisent pas d'énergie ⇒ pour que le moteur fonctionne à une vitesse constante on va chercher de l'énergie additionnelle dans l'énergie cinétique accumulée dans un volant adossé au moteur.
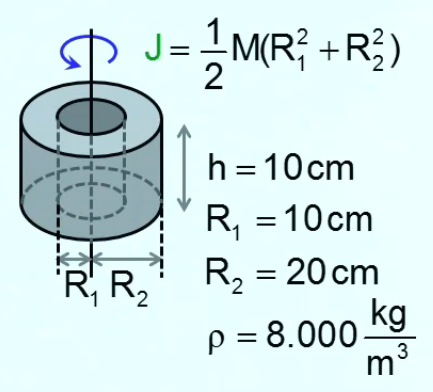
Pour calculer son énergie cinétique on utilise la formule du moment d'un anneau (graphique ci-contre), obtenue par le calcul d'intégration de volumes ébauché supra :
J = 1/2 * M * ( R12 + R22 ) ⇒
en injectant les valeurs du schéma ci-contre (la valeur de ρ est celle de l'acier) on trouve :
J ≈ 1,9 kg*m2
On suppose que le moteur tourne à une fréquence de :
f = 2.400 tour/min = 40 tr/s (= Hz)
or la fréquence est par définition l'inverse de la période T ⇒
ω = 2 * π / T ≈ 251 Hz (186) ⇒
Ec = J * ω2 / 2 ≈ 1,9 * 2512 / 2 ≈ 60.000 J
ce qui représente l'énergie nécessaire pour envoyer une masse de 1kg à une hauteur de 6.000 mètres :
⇒ L = 60.000 / 10 = 6.000 m
Le tableau suivant compare les formules de (moment) de force, énergie et vitesse selon le type de mouvement.
| (Moment de) Force | Énergie | Vitesse | |
|---|---|---|---|
| Rectiligne | m * d2x / dt2 = f | Ec = m * v2 / 2 | v = dx /dt |
| Rotation | ( ∑n=1N mn * rn2 ) * d2θ / dt2 = τ | Ec = J * ω2 / 2 | ω = dθ / dt |
Ainsi dans le MRUA la force d'inertie exercée sur le corps est déterminée par la masse m tandis que dans le mouvement de rotation elle est déterminée par le moment d'inertie J = ∫n=1N ρ * dVn * rn2.