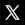IV. Algèbre
Résolution de problèmes
N.d.A. Ce résumé diffère quelque peu de l'approche adoptée dans la vidéo. Je suis seul responsable des différences de forme comme de fond.
La résolution d'un problème mathématique consiste à déterminer un système d'équations :
formalisant les relations entre variables (inconnues) et paramètres (connus) ;
dont le nombre est égal au nombre de variables (en effet, si le nombre d'équations est inférieur au nombre d'inconnues, on ne peut calculer la valeur de ces dernières : un système "sous-déterminé" est non résoluble).
La première phase de cette démarche consiste à écrire le pseudo-code de l'équation, c-à-d une description informelle, la plus simple possible, des relations existant entre inconnues et paramètres :
| Second exemple de la vidéo | Premier exemple de la vidéo | |
| Pseudo-code | L'âge que j'avais il y a dix ans est la moitié de celui que j'aurai dans dix ans. |
|
|---|---|---|
| Équations | A - 10 = ( A + 10 ) / 2 |
Pb * Qb + Ps * Qs = C
Ps = Pb / 2 |
| Résolution | A = ( 10 / 2 + 10 ) * 2 |
Pb * Qb + Pb / 2 * 15 = C ⇒
Pb * 85 + Pb / 2 * 15 = 130 ⇔ Pb = 130 / ( 85 + 15 / 2 ) |
Fonction
Pour illustrer de façon pratique la notion de fonction mathématique, on va étudier le fonctionnement d'une machine-outil, commandée par un ordinateur, et permettant l'usinage d'une pièce métallique. La pièce en question est un cylindre métallique, que la machine-outil peut sculpter de façon programmée, en quelques secondes.

Principes de
la machine
Le principe de fonctionnement est assez simple. L'outil de découpage peut se déplacer dans deux directions relativement au cylindre : parallèlement (cf. moteur vert ci-dessous) et perpendiculairement (cf. moteur bleu). En activant simultanément les deux moteurs, on peut appliquer au bras du couteau une série de déplacements, par exemple le mouvement rectiligne et incliné vers la droite illustré ci-dessous.

L'ordinateur (à gauche) commande les deux moteurs : le bleu (déplacement perpendiculaire à l'axe du cylindre, vertical sur ton écran) et le vert (déplacement parallèle à l'axe du cylindre, horizontal sur ton écran).
N.d.A. Je suppose qu'il n'y a pas besoin de mouvement vertical pour le couteau puisque le cylindre est en rotation autour de son axe.
Pour obtenir une trajectoire précise, par exemple la ligne droite du schéma, il faut que pour chaque déplacement horizontal (noté h) le déplacement vertical (noté v) prenne la valeur précise correspondante. Le schéma suivant représente un déplacement linéaire tel que v = 1,25 * h. Cette relation entre les déplacements v et h caractérise le tracé du déplacement, et s'applique à tous les points de la trajectoire : pour un déplacement de 1 cm vers la droite, il faut un déplacement vertical de 1,25 cm.

La relation v = 1,25 * h vaut pour tous les triangles correspondant à une flèche/hauteur verticale bleue.
C'est cette relation entre deux ensembles de nombres (ici les ensembles v et h) que l'on appelle "fonction".
Le rôle de l'ordinateur de la machine-outil est de déterminer une série de valeurs de h, séparées par un pas constant, puis de calculer les valeurs correspondantes de v, au moyen de la fonction v = 1,25 * h. Le résultat de ce traitement mathématique/informatique est enregistré dans une table de valeurs composée de deux colonnes :
- colonne des valeurs de h ;
- colonne des valeurs de v correspondantes.
Cette table des valeurs est donc l'expression numérique de la fonction qui permet de générer ces valeurs. L'expression mathématique (ou analytique) de la fonction est ici v = 1,25 * h, et son expression graphique est la trajectoire du schéma.
Usinage
sphérique
Pour approfondir la notion de fonction, passons à un usinage consistant à réaliser une demi-sphère à l'extrémité du cylindre d'acier. Pour ce faire il n'est besoin de déterminer qu'un quart de cercle puisque le cylindre est en rotation autour de son axe (qui est perpendiculaire à celui du bras de découpage).

Comment programmer l'ordinateur pour qu'il suive cette trajectoire en quart de cercle ? Une méthode (pas très efficace) consisterait à dessiner le quart de cercle d'un rayon de 5 cm sur une feuille de papier, puis de mesurer au moyen d'une règle les positions v et h (en cm) d'une série de points de cette trajectoire, et enfin de répertorier ces mesures dans une table des valeurs, que l'ordinateur pourra alors utiliser pour diriger le bras de la machine-outil.

Mais cette méthode de mesure expérimentale et manuelle est imprécise : la courbe a-t-elle été dessinée correctement, et les positions d'une série de ses points ont-elles été mesurées avec précision ? Il est donc fort probable que le découpage du cylindre réalisé par la machine-outil sur base des ces données imparfaites serait imparfait. Et puis, étant donné que la trajectoire contient une infinité de points, la série de points qu'un humain peut traiter est très limitée ⇒ on pourrait relier ces points par une droite, mais le résultat de l'usinage ne sera alors pas très lisse. Idéalement il nous faudrait donc pouvoir mesurer la position de tous les points de la trajectoire. Mais il y en a une infinité ...
Calculer, plutôt que mesurer. Une méthode alternative, plus efficace que la mesure expérimentale (manuelle) d'une série de valeurs de h, est l'abstraction mathématique. Pour ce faire on va représenter graphiquement les positions v et h.

Il apparaît alors que le rayon de 5 cm détermine un triangle rectangle de base h et hauteur v, ce qui nous permet d'appliquer le théorème de Pythagore pour formuler la relation entre v, h et R=5 :
52 = v2 + h2 ⇔
v = √ ( 25 - h2 )
fonction qui est valable pour tous les points de la trajectoire, ce qui nous permet d'obtenir une précision absolue : pour toute valeur de h, on peut ainsi calculer la valeur de v exactement correspondante. Cela permet d'obtenir pour le façonnage du cylindre un degré de précision arbitrairement élevé : il suffit pour cela de choisir un pas aussi fin que nécessaire pour la progression de h, et donc, via la fonction, pour la progression de v.

Table des valeurs de la fonction
Concrètement, on va programmer l'ordinateur pour qu'il détermine une série de valeurs de h qui évoluent par pas d'un demi millimètre (on pourrait choisir un pas encore plus petit si nécessaire).
L'avantage de l'ordinateur – par rapport à un calcul "manuel" réalisé par un opérateur humain – est qu'il peut traiter beaucoup plus vite un nombre de données beaucoup plus grand, ce qui permet d'obtenir une précision très fine du découpage du cylindre.
Analysons maintenant cette relation mathématique v = √( 25 - h2 ), que l'on appelle "fonction" car elle exprime le fait que les valeurs de v sont calculées en fonction des valeurs de h. Et pour formuler cela, une convention est de noter la fonction comme suit : v(h) = √( 25 - h2 ) où h est appelée la "variable".
Pour faire le lien entre le dessin de la trajectoire et sa fonction, on complète la trajectoire par des axes pour la mesure de v et h, ce qui nous donne le graphe de v(h).

Graphe de la fonction
Le concept mathématique de fonction repose donc sur trois représentations :
- table des valeurs ;
- graphe ;
- notation mathématique.
Intéressons-nous maintenant à la relation entre le graphe et la notation mathématique de la fonction.
Relation univoque. Par définition la valeur d'une fonction doit être unique : la relation qu'elle formalise est dite univoque. Il en résulte que, par convention √(x2) = |x| : √(9) = 3 et non ± 3 ! Ainsi dans notre application de machine outil, l'ordinateur sera contraint de poser que :
v(4) = √( 25 - 42 ) = √(9) = 3
Le schéma suivant illustre le fait que si l'ordinateur choisissait la valeur -3, cela provoquerait le découpage de la sphère, puisque le couteau de la machine irait jusqu'en bas du cercle au lieu de s'arrêter à la base du quart de cercle...

Domaine des valeurs. Prenons maintenant la valeur h=6 : quelle est alors la valeur correspondante de v(6) ? Zéro ? Pour vérifier, il suffit de calculer la valeur au moyen de la fonction :
v(6) = √( 25 - 62 ) = √(-11) = ?
Or, par définition, la racine d'un nombre réel est telle que le carré de la racine vaut ce nombre. Et d'autre part le carré d'un nombre réel négatif est positif. Par conséquent il n'y a pas de solution pour la racine carrée d'un nombre réel négatif ...
Nous allons donc devoir limiter le domaine des valeurs de v(h), ce que l'on exprime mathématiquement comme suit :
Dv : h ∈ [ 0 , 5 ]
On doit toujours assortir l'expression mathématique d'une fonction par son domaine de définition , qui fait donc partie intégrante de la définition de la fonction.
Observons maintenant le cas des valeurs négatives de h. Puisque h est au carré dans v(h) = √( 25 - h2 ) nous obtiendrons la même valeur de fonction que pour les mêmes nombres de signe positif. On peut donc avoir plusieurs valeurs de h pour une même valeur de v(h) ⇔ cette fonction n'est pas biunivoque (rappel : toutes les fonctions sont au moins univoques).

(-4)2 = 42 ⇒ v(-4) = v(4) = √( 25 - 16 ).
Ainsi l'animation infra illustre deux programmations de découpage :
- si l'on souhaite compléter la sphère par un manchon de 1 cm, le domaine doit être Dv : h ∈ [ -4 , 5 ]
- si l'on souhaite découper complètement la sphère, le domaine doit être Dv : h ∈ [ -5 , 5 ]

Notez la barre verticale hachurée qui apparaît dans le graphe de l'image 1/2, où la sphère n'est pas coupée du manchon.
Notation standardisée. La variable est souvent noté génériquement par la lettre x, tandis que la fonction est logiquement notée par la lettre f. Cependant, l'axe vertical du graphe ne sera pas noté f(x) mais y, car cet axe ne désigne pas la fonction mais ses valeurs ! La fonction est représentée par l'ensemble du graphe, comprenant les deux axes, et donc l'ensemble de leurs valeurs. La notation y = f(x) exprime non pas la fonction mais un couple de valeurs (x,y) déterminé par cette fonction : y est l'image de la variable x, par la fonction.

Quelques exemples de fonctions complexes utilisées dans de nombreuses applications technologiques :
La parabole de tir exprime la trajectoire d'un objet projeté dans l'espace. Elle comprend des paramètres : vitesse du lancé (v), angles du lancé (α), hauteur maximale de la trajectoire (h) :

La fonction harmonique, permet de représenter une onde électromagnétique (telle que celle émise par un laser). Elle implique deux variables : l'espace (x) et le temps (t) :

La fonction gaussienne permet notamment de représenter des résultats statistiques, comme la distribution des tailles dans une population, qui fait apparaître des tailles plus fréquentes que d'autres :

La fonction harmonique sphérique permet de décrire le comportement d'un atome (ici les différents états du nuage électronique de l'atome d'hydrogène).

Calcul infinitésimal
L'essentiel du calcul infinitésimal, en tant que technique algébrique (notamment le calcul différentiel et intégral), a été développé aux 16° et 17° siècle. Cependant, ses principes géométriques avait été établis dès l'antiquité.
Ainsi, dès le 5° siècle av. J.-C., le philosophe Antiphon avait proposé de calculer la circonférence du cercle en assimilant celui-ci à un polygone régulier à N côtés de longueur L. Le périmètre de ce polygone vaut donc N * L, et approchera la circonférence du cercle d'autant plus que N sera grand (NB : ce qui a comme effet corrélatif que L devient de plus en plus petit). Le raisonnement d'Antiphon peut être formulé comme suit : P = N * L ≈ C. La difficulté est donc réduite à la connaissance de L (par la mesure ou le calcul) étant donné N.
C'est en appliquant ce principe que deux siècles plus tard Archimède a conçu des formules pour calculer le périmètre du cercle C = 2 * π * R (26). Et ce faisant, il a conçu une méthode permettant de calculer la valeur de π (25) avec autant de précision que souhaité.
Archimède est parti d'un hexagone, dont la particularité est qu'il est composé de triangles équilatéraux, et dont la longueur des côtés est à la fois la longueur L des côtés de l'hexagone, et le rayon R du cercle correspondant.
N.d.A. La couleur du P du schéma de droite devrait être noire.
Dans ces conditions, soient :
• P : le périmètre de l'hexagone ;
• C : la circonférence du cercle ;
alors, étant donné que :
P = 6 * R ≈ C
et
C = 2 * π * R (26)
⇒ si on substitue la valeur de C de la première égalité dans la seconde, on obtient :
6 * R ≈ 2 * π * R ⇔
π ≈ 3
Pour augmenter la précision du calcul (le nombre de décimales de π) Archimède poursuit alors le raisonnement d'Antiphon consistant à augmenter la valeur de N, en concevant une formule lui permettant de calculer L à chaque fois qu'on multiplie N par 2. Sa formule devient de plus en plus complexe au fur et à mesure des doublements, de sorte qu'il n'a pas été plus loin qu'un polygone à N=96 côtés, ce qu'il lui a permis de calculer la valeur de π = 3,14. Aujourd'hui, grâce aux ordinateurs, on peut appliquer la méthode algébrique d'Archimède pour augmenter considérablement la précision du calcul de π (par exemple pour N=196.608 on trouve π=3,141592).
Mais est-il ici pertinent de poser que N = ∞ ? Pour répondre à cette question, il faut commencer par constater que dans ce cas L = 0 puisque plus N augmente, plus L devient petit.
Mathématiquement, on exprime cela comme suit :
P = N * L ⇔
L = P / N ⇒
L = P / ∞ = 0
Dans ce cas, le raisonnement d'Antiphon est formulé algébriquement comme suit :
P = N * L ≈ C
⇒
P = ∞ * 0 = C
Mais il y a un problème : ∞ * 0 est une forme indéterminée ...
Ce problème va être résolu par le calcul infinitésimal, dont le principe est ici que :
N ne doit pas être égal à l'infini mais seulement "arbitrairement grand" (entendu "aussi grand que nécessaire") c-à-d "tendre vers l'infiniment grand" ... tout en restant un nombre fini (il n'est donc pas "infiniment grand") ;
⇒ L = P / N n'est pas égal à zéro mais seulement "arbitrairement petit" (entendu "aussi petit que nécessaire") c-à-d "tendre vers l'infiniment petit" (c-à-d zéro) ... tout en restant un nombre fini (il n'est donc pas "infiniment petit" donc pas nul).
Le concept de "grandeur infinitésimale" (N.d.A. : que l'on pourrait noter par les indices "→∞" et "→0") permet alors de formuler correctement le raisonnement d'Antiphon comme suit :
P = N * L ≈ C
⇒
P = N→∞ * L→0 = C
N.d.A. Les grandeurs "arbitrairement grandes" et les grandeurs "arbitrairement petites" sont dites "grandeurs infinitésimales".
Le concept de décomposition infinitésimale consiste à obtenir une grandeur (par exemple la circonférence C du cercle) à partir d'un nombre arbitrairement grand (ici le nombre N de côtés du polygone régulier inscrit dans le cercle) de grandeurs arbitrairement petites (ici la longueur L des côtés de ce polygone) :
soient P le périmètre du polygone, et C la circonférence du cercle :
P = N * L ≈ C
⇒ décomposition infinitésimale ⇒
P = N→∞ * L→0 = C
La couleur rouge ci-dessus signifie que la décomposition infinitésimale permet de considérer que, à la limite, le périmètre de l'hexagone n'est plus seulement une approximation de la circonférence du cercle, mais bien égal à celle-ci.
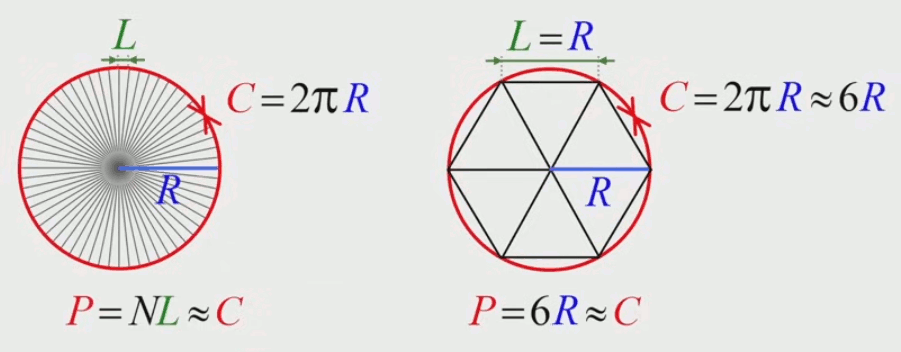
C'est le principe appliqué par Archimède pour déterminer la formule de la surface S = π * R2 (27) du cercle. Sa méthode consiste à décomposer et approcher la surface du cercle par celle (de la somme) des triangles isocèles composant un polygone régulier inscrit dans ce cercle.
Soient :
• SP : la surface du polygone ;
• N : le nombre de côté du polygone (et donc aussi le nombre de triangles) ;
• ST : la surface de chacun de ses triangles ;
on a alors :
SP = N * ST
de sorte que l'on peut considérer que la surface du polygone est une approximation de la surface du cercle :
SP = N * ST ≈ S
et le raisonnement de décomposition infinitésimale postule alors que cette approximation devient une égalité lorsque N tend vers l'infini (et que donc ST tend vers zéro) :
SP = N→∞ * ST→0 = S
Pour montrer que ce passage de l'approximation à l'égalité n'est pas une passage en force, on va formaliser le fait que l'approximation d'une grandeur (par la mesure ou le calcul), c'est cette même grandeur ... plus une "erreur d'approximation" (en l'occurrence il s'agit de l'erreur commise en approximant la surface du cercle par celle du polygone régulier lui correspondant).

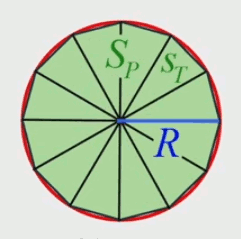
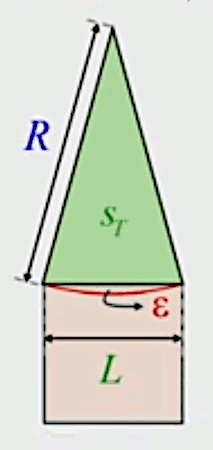
Pour formaliser tout cela, intéressons-nous aux triangles isocèles composant le polygone, et dont la base L est la longueur des côtés de ce polygone. La grandeur que l'on veut mesurer in fine ce n'est pas la surface d'un triangle, mais celle d'un "quartier de tarte", qui est l'addition de ce triangle et de la différence entre les deux c-à-d l'erreur d'approximation (notée epsilon) :
SQ = ST + ε
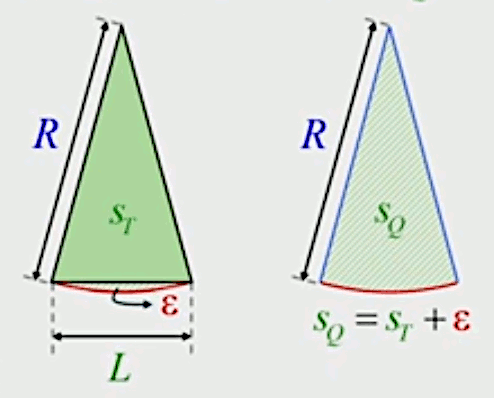
On peut maintenant développer la formulation de la surface du cercle :
S = N * SQ ⇒
S = N * ( ST + ε ) ⇔
S = N * ST + N * ε ⇔
S = SP + N * ε
Rappel. Dans la vidéo précédente, nous avons vu qu'Archimède avait mis au point une méthode lui permettant de calculer L à chaque fois qu'on multiplie par 2 le nombre N de côtés de l'hexagone.
À priori, l'erreur N * ε commise en estimant S par SP pose question. En effet, lorsque N tend vers l'infini, l'erreur ε du "quartier de tarte" tend vers zéro, de sorte que le produit N→∞ * ε→0 est à priori indéterminé. Se pose alors la question : comment peut-on affirmer que dans la configuration présente le produit N→∞ * ε→0 tend vers zéro lorsque N tend vers l'infini ?
Pour lever cette indétermination, on va appliquer une méthode classique du calcul infinitésimal, consistant en l'occurrence à comparer la surface ε à la surface du carré de côté L. Or il est évident que la première est inférieure à la seconde :
ε < L2 ⇔
N * ε < N * L2 ⇒
N * ε < N * ( P / N )2 ⇔
N * ε < P2 / N ⇒
N→∞ * ε < ( P2 / N→∞ )→0 ⇒
( N→∞ * ε )→0
CQFD
L'erreur n'est pas nulle, mais elle tend clairement vers zéro lorsque N tend vers l'infini. Concrètement, cela signifie qu'on peut toujours choisir une valeur de N, "arbitrairement grande", telle que l'erreur peut être considérée comme négligeable, ce qui autorise le passage conceptuel de l'approximation vers l'égalité.
Autre exemple. Pour nous familiariser avec la méthode de décomposition infinitésimale, nous allons l'appliquer pour déterminer la formule de la surface du triangle rectangle et isocèle, en décomposant celui-ci en une série de N rectangles de même largeur.
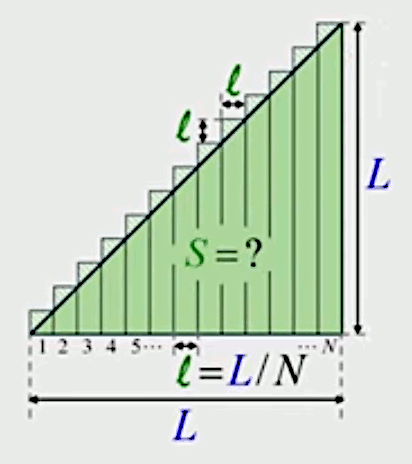
La base de ces rectangles est l = L /N, et comme le triangle est isocèle, il en va de même des côtés de même longueur des petits triangles rectangles isocèles qui constituent l'erreur de l'estimation de la surface du triangle par celle de la somme des rectangles.
Par (19), la surface ε de chacun des triangles d'erreur est donc ε = l 2 / 2. L'erreur d'approximation de la surface du triangle est donc ici de N * ε = N * l 2 / 2.
N.d.A. Le lecteur attentif aura noté qu'il y a auto-référence (raisonnement circulaire) : la formule de la surface du triangle est obtenue à partir ... d'elle-même. Cependant il ne s'agit pas ici d'une démonstration, mais d'une illustration de la décomposition infinitésimale, cette fois d'un triangle par des rectangles, et plus d'un cercle par des triangles.
D'autre part, il résulte de notre configuration que la première colonne est un carré de surface l 2, la deuxième un rectangle de surface 2 * l 2, etc, la ne colonne étant un rectangle de surface n * l 2.
Soit SP la surface du polygone constitué par les rectangles, on a donc que :
S ≈ SP = l 2 + 2 * l 2 + 3 * l 2 + ... + N * l 2 ⇔
S ≈ SP = l 2 * ( 1 + 2 + 3 + ... + N ) ⇔ par (124) :
S ≈ SP = l 2 * N * ( N + 1 ) / 2 ⇔
S ≈ SP = ( l 2 * N2 + l 2 * N ) / 2 ⇔
S ≈ SP = ( L2 + l 2 * N ) / 2 ⇔
S ≈ SP = L2 / 2 + l 2 / 2 * N ⇔
S ≈ SP = L2 / 2 + ε * N ⇔
S ≈ SP = L2 / 2 + L 2 / N 2 / 2 * N ⇔
S ≈ SP = L2 / 2 + L 2 / N / 2 ⇔
S ≈ SP = L2 / 2 + ( L 2 / N→∞ / 2 )→0 ⇔
S ≈ SP = L2 / 2 + ( ε * N→∞ )→0 ⇒
S = SP
Ce résultat a été obtenu par la décomposition du triangle en un nombre N arbitrairement grand de rectangles d'une largeur l arbitrairement petite.
La calcul infinitésimale nous permettra de réaliser des calculs de natures très différentes :
- surface et volume de la sphère et du cône ;
- le centre de gravité d'un cône ;
- la masse d'un corps dont la masse volumique varie en fonction de la position dans le corps ;
- le champ électrique d'une tige uniformément chargée ; ...
Mais pour cela, il nous faudra faire appel aux notions de dérivée et d'intégrale ...
Dérivée
La dérivée f '(x) = df(x) / dx c'est la pente de la courbe, ou encore la sensibilité (c-à-d le taux de variation) de f(x) par rapport à x. Ainsi si x est le temps écoulé et f(x) la distance parcourue alors ce taux de variation est la vitesse. Nous allons voir que la dérivée correspond à la vitesse dite "instantanée" c-à-d en un point déterminé, par opposition avec la vitesse moyenne Δy / Δt c-à-d entre deux points déterminés.
C'est de cette vitesse moyenne que nous allons d'ailleurs déduire celle de vitesse instantanée. La vitesse est constante ⇔ la pente de la courbe est constante en tous points (droite verte). Ou encore la pente de la droite verte représente la vitesse moyenne de la courbe rouge.

De même, l'on pourrait calculer la vitesse sur seulement un segment de la fonction, comme illustré dans le graphique suivant.
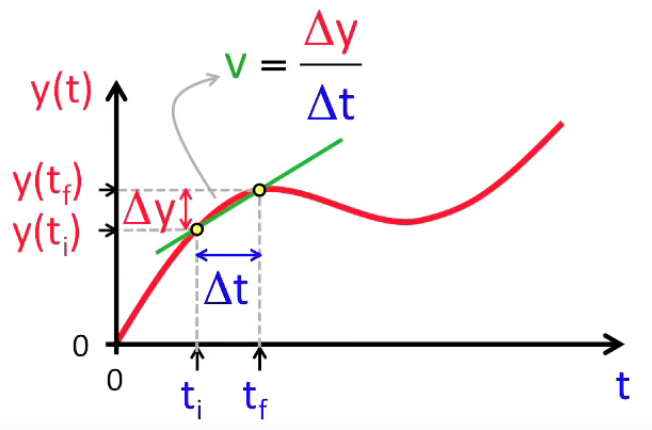
Le principe de la dérivée est alors qu'en diminuant Δt = tf - ti "à l'infini" c-à-d jusqu'à une valeur "arbitrairement proche de zéro" (infinitésimale), on pourra toujours atteindre une échelle suffisamment petite pour que le segment de la courbe déterminé par Δt puisse être considéré comme une droite.
Ainsi Δy et Δt tendent tous les deux vers zéro, mais leur ratio est constant (puisqu'il le segment infinitésimal peut être considéré comme une droite) et vaut :
v(t) = limΔt → 0 Δy / Δt ⇔
v(t) = limΔt → 0 ( y( t + Δt ) - y(t) ) / Δt
que l'on simplifie en posant que :
si Δt → 0 alors Δt = dt
:
(approche dite "différentielle", qui est donc une différence infinitésimale, permettant de passer d'une description discrète à un continuum ; en l'occurrence on passe ici de la notion de vitesse moyenne à celle de vitesse instantanée)
⇒
v(t) = ( y( t + dt ) - y(t) ) / dt ⇔
v(t) = dy(t) / dt
Généralisation : la dérivée d'une fonction f(x) est le rapport entre la différentielle de la fonction f(x) et la différentielle de la variable x :
f '(x) = df (x) / dx = ( f ( x + dx ) - f (x) ) / dx
La première égalité définit la notation simplifiée.
Le deuxième égalité définit le mode de calcul.
Exemples :
Soit la fonction :
f (x) = x2
appliquée à (81) ⇒
d(x2) / dx = ( ( x + dx )2 - x2 ) / dx ⇔
d(x2) / dx = ( ( x2 + 2 * x * dx + dx2 ) - x2 ) / dx ⇔
d(x2) / dx = 2 * x + dx
où par définition dx peut-être arbitrairement petit et donc considéré comme négligeable par rapport à 2*x ⇒
d(x2) / dx = 2 * x
f(x) quelconque
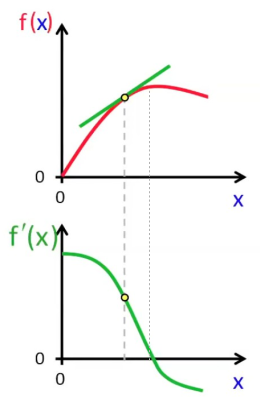
La dérivée est elle-même une fonction (exemple à partir d'une f(x) quelconque).
Soit la fonction :
f (x) = 1 / x
appliquée à (81) ⇒
d(1/x) / dx = ( 1 / ( x + dx ) - 1 / x ) / dx ⇔
en réduisant le numérateur au même dénominateur :
d(1/x) / dx = - 1 / ( x 2 + x * dx )
où par définition dx peut-être arbitrairement petit, de sorte que x*dx peut être considéré comme négligeable par rapport à x2 ⇒
d(1/x) / dx = - 1 / x 2
Propriétés
À partir de f '(x) = df (x) / dx = [ f ( x + dx ) - f (x) ] / dx (81) on démontre les propriétés suivantes.
Dérivée d'une somme de fonction :
d( ∑ fi (x) ) / dx =
[ ∑ fi (x + dx) - ∑ fi (x) ] / dx =
la différence de sommes est une somme de différences :
[ ∑ ( fi (x + dx) - fi (x) ) ] / dx =
distribution de 1/dx :
∑ [ ( fi (x + dx) - fi (x) ) / dx ] =
∑ ( dfi (x) / dx )
La dérivée d'une somme de fonction est la somme des dérivées.
Dérivée d'un produit de fonctions :
d( π fi (x) ) / dx =
[ π fi (x + dx) - π fi (x) ] / dx =
par définition de dfi (x) = fi (x + dx) - fi (x) :
[ π ( fi (x) + dfi (x) ) - π fi (x) ] / dx = ?
Si l'on continue la démonstration sur cette voie générale ça va devenir difficilement lisible ⇒ on va plutôt passer par les cas n=2 et n=3 ; en outre, toutes les fonctions de la dernière étape étant en x, on va simplifier l'écriture en remplaçant f(x) par f :
n=2 :
d( f * g ) / dx =
[ ( f + df ) * ( g + dg ) - f * g ] / dx =
[ f * g + f * dg + df * g + df * dg - f * g ] / dx =
f * g ' + f ' * g + df * dg / dx =
f * g ' + f ' * g + f ' * g' * dx ⇔
( f * g )' = f ' * g + f * g '
n=3 :
d( f * h * i ) / dx =
en posant g(x) = h(x) * i(x) dans (85) :
f * ( h * i ) ' + f ' * ( h * i ) =
f * ( h * i' + h' * i ) + f ' * ( h * i ) =
f * h * i' + f * h' * i + f ' h * i )
où l'on constate une symétrie : le signe de dérivée passe progressivement d'un côté à l'autre, ce que l'on peut généraliser comme suit :
( π1 n fi )' = ∑i=1 n ( fi' *
π1 i-1 fi *
π i+1 n fi )
(si on convient que π n+1 n fi = 1)
Ainsi dans le cas particulier fi = f ∀ i :
( f n ) ' = n * f n-1 * f '
dont deux cas particuliers sont les fonctions :
- identité : f (x) = x ⇒
( x n ) ' = dx n / dx = n * x n-1 - inverse : f (x) = 1 / x = x -1 ⇒
( x - n ) ' = dx - n / dx = - n * x -n-1
Dérivée d'un quotient de deux fonctions :
d( f (x) / g (x) ) / dx = d( f / g ) / dx =
d( f * g - 1 ) / dx ⇔
par (82) :
d( f / g ) / dx = f ' * g - 1 + f * g - 1 ' ⇔
par (83) :
d( f / g ) / dx = f ' * g - 1 - f * g - 2 * g ' ⇔
d( f / g ) / dx = ( f ' * g - f * g ' ) / g 2
Cependant la démonstration ci-dessus est incomplète car elle repose sur l'hypothèse non démontrée que (83) vaut également pour les entiers (n) négatifs. Pour démontrer cette hypothèse on va développer la différentielle d'un quotient particulier : f - n, cela en partant de sa définition :
f n * f - n = 1 ⇔
( f n * f - n ) ' = 0 ⇔
par (85) :
( f n ) ' * f - n + f n * ( f - n ) ' = 0 ⇔
( f - n ) ' = - ( f n ) ' * f - 2n ⇔
( f - n ) ' = - n * f n-1 * f ' * f - 2n ⇔
( f - n ) ' = - n * f -n-1 * f '
CQFD.
Dérivée de fonctions trigonométriques :
dcos(α) / dα = [ cos(α + dα) - cos(α) ] / dα ⇔
par cos(a+b) = cos(a) * cos(b) - sin(a) * sin(b) (42) :
dcos(α) / dα = [ cos(α) * cos(dα) - sin(α) * sin(dα) - cos(α ] / dα ⇔
dcos(α) / dα = - sin(α) * sin(dα) / dα ⇒
par démonstration infra de sin(dα) = dα :
dcos(α) / dα = - sin(α)
Et on démontre de la même manière, cette fois à partir de (41), que :
dsin(α) / dα = cos(α)
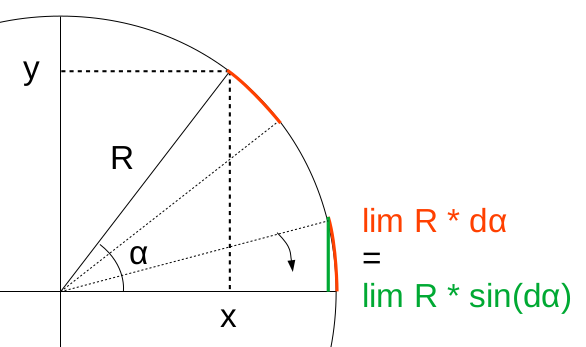
L'égalité sin(dα) = dα se démontre géométriquement à partir des définitions de l'angle radian (1) et du sinus (31) : graphique ci-contre : la variation infinitésimale dα d'un angle α correspond à l'égalité "à la limite" entre l'arc-tangente (en rouge) et le sinus (en vert) : limα→0 sin(Δα) / dα = 1
Dérivée d'une fonction composée :
la démonstration est triviale :
dF( G(x) ) / dx =
dF( G(x) ) / dG(x) / ( dx / dG(x) ) ⇔
dF( G(x) ) / dx = dF( G(x) ) / dG(x) * dG(x) / dx ⇔
( F[ G(x) ] )' = F'( G(x) ) * G'(x)
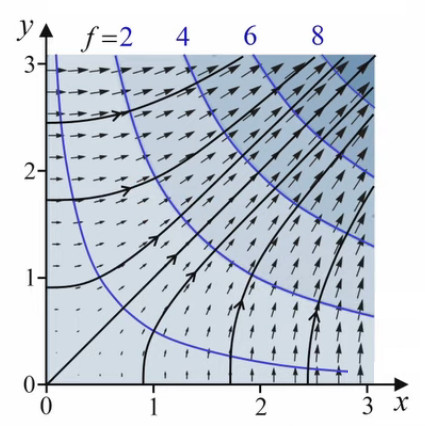
Gradient et dérivée directionnelle
Le gradient (∇→) est un objet mathématique fondé sur les notions de dérivée partielle et de dérivée directionnelle. Il permet notamment de décrire des variations d'une grandeur (pression, température, ...) entre une série de points dans l'espace. En voici quatre exemples :
-
ρ * dv→ / dt = - ∇→P + μ * Δv→ + ρ * F→ : dans cette équation de mécanique des fluides, le gradient de la pression exprime le déplacement d'air de la gauche vers la droite de cette aile d'avion, par la diminution de la pression de l'air, de la gauche vers la droite.

-
J→ = - kT * ∇→T : dans cette équation de conduction thermique, le gradient de la température exprime le fait que la chaleur diffuse des points les plus chauds vers ceux de plus basse température.

-
dx→ / dl = 1 / n(x→) * ∇→φ(x→) : dans cette équation d'optique géométrique, le gradient de la phase du champ électromagnétique détermine la direction des rayons lumineux.

-
x→k+1 = x→k - α(k) * ∇→f(x→k) : cette équation est extraite d'un algorithme d'optimisation permettant de trouver les extrema de la fonction complexe représentée dans l'image ci-contre.
C'est ce dernier cas d'optimisation (mais avec une fonction plus simple) que nous allons utiliser ici pour développer la notion de gradient, et illustrer son utilité.
Pour ce faire le problème d'optimisation que nous allons résoudre ici est le suivant : dans quelle direction faut-il tirer sur un des angles d'un rectangle pour obtenir le plus grand accroissement de surface (pour une longueur d'étirement Δl→ déterminée) ?
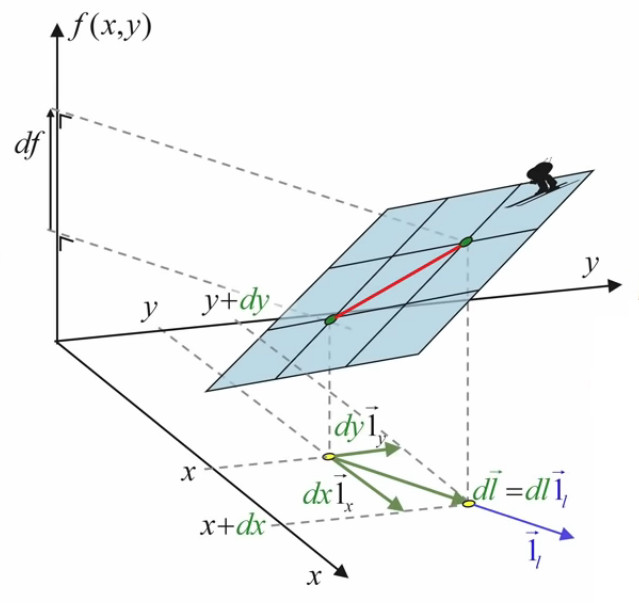
Pour répondre à cette question on va commencer par introduire un repère cartésien, de sorte que l'on va pouvoir exprimer la surface du rectangle en terme des coordonnées (x,y) du point d'étirement :
S = x * y ⇔ f(x,y) = x * y
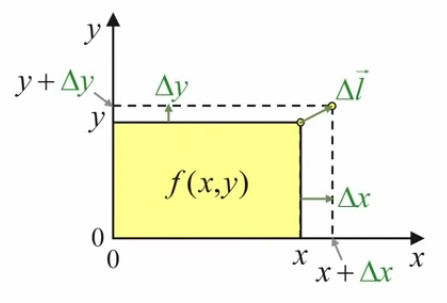
Quant au déplacement du point d'étirement, on peut le représenter par le vecteur Δl→, dont les composantes en x et y sont Δx et Δy ⇔ par (56) :
Δl→ = Δx * 1x→ + Δy * 1y→
Et l'accroissement du rectangle (Δf) se formule par :
f(x+Δx,y+Δy) - f(x,y) = ( x + Δx ) * ( y + Δy ) - x * y
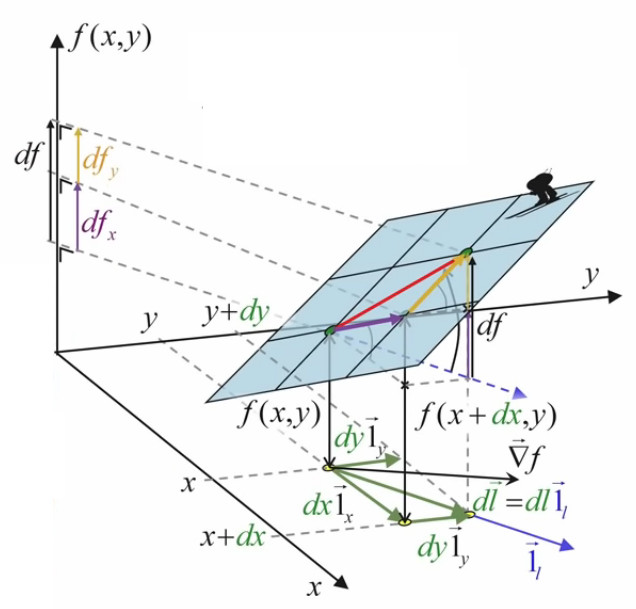
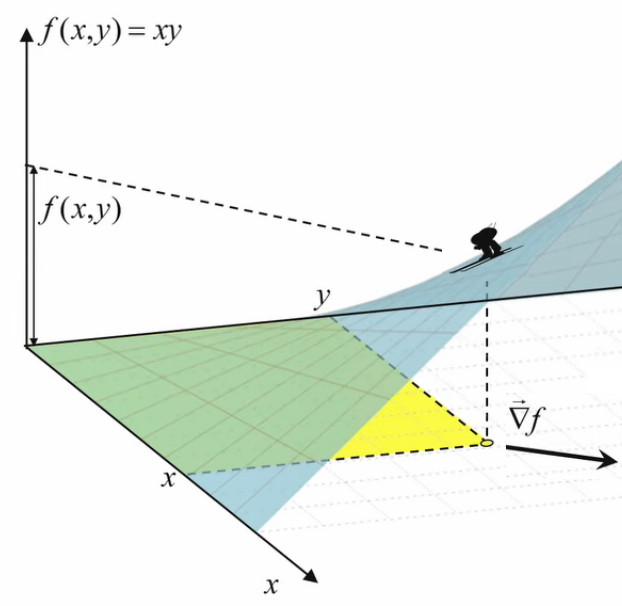
L'image ci-dessous montre que le graphe de la fonction f(x,y) est elle-même une surface.
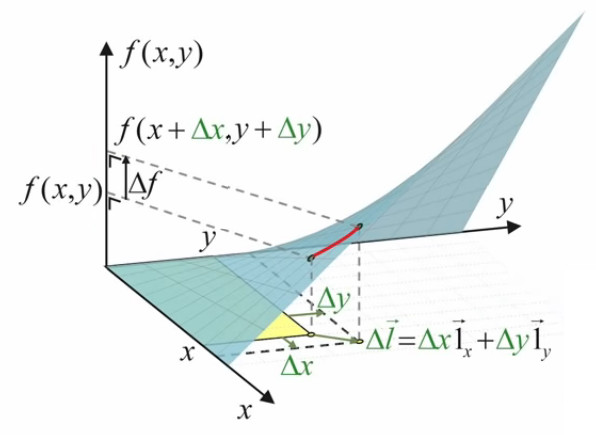
N.B. Lorsque l'on par de "la surface f(x,y)", il convient de distinguer :
- la surface rectangulaire jaune, correspondant à une valeur déterminée de (x,y) ;
- la surface bleue, qui est la représentation graphique de toutes les valeurs que peut prendre la surface jaune.
Il nous faut maintenant formaliser l'orientation du vecteur d'étirement Δl→. Pour ce faire on va introduire le vecteur unitaire de direction 1l→, ce qui permet d'exprimer Δl→ non plus seulement par :
Δl→ = Δx * 1x→ + Δy * 1y→
mais aussi par :
Δl→ = Δl * 1l→
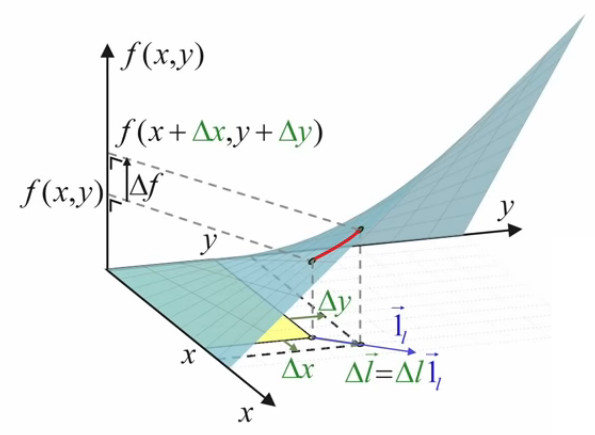
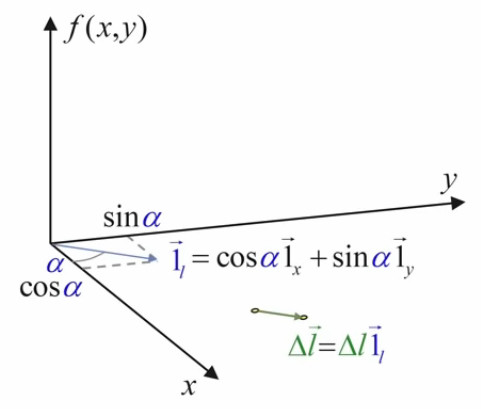
La valeur de ce vecteur unitaire de direction est donnée – via (56), (31) et (32) – par :
1l→ = cos(α) * 1x→ + sin(α) * 1y→
t76
L'étape suivante de la formalisation de notre problème d'optimisation consiste à passer de Δl à dl (80) c-à-d à un accroissement arbitrairement petit. En effet si le vecteur d'étirement est trop grand, on risque de "dépasser l'optimum" sur la surface f(x,y) c-à-d en fait, redescendre en-dessous de la valeur de cet optimum.
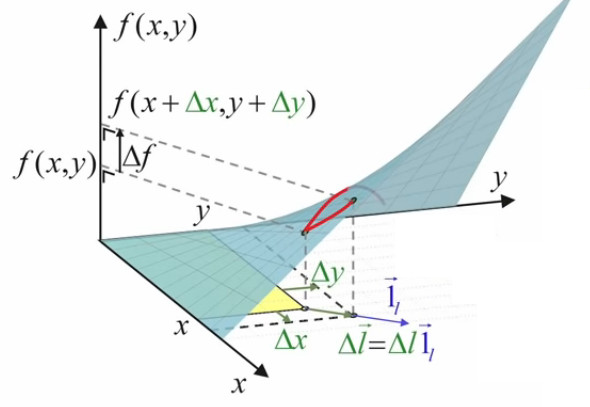
Or, en-dessous d'une certaine longueur, un segment de courbe peut être considéré comme une droite ⇒ le remplacement de Δl par la différentielle dl (80) permet d'approcher la valeur recherchée de l'optimum de surface (NB : le remplacement de Δl par dl implique géométriquement celui de Δf par df).
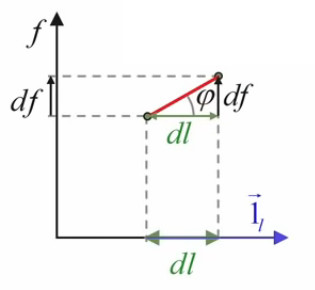
Dans ces conditions, ce que l'on optimise est alors tout simplement la pente df / dl.
Et par (47) :
df / dl = tg(φ) ⇔
deriv-dir-tg
df = tg(φ) * dl
c-à-d que la différentielle de f vaut le produit de sa pente tg(φ) par le déplacement dl.
Le problème est maintenant clairement posé : on cherche à déterminer l'orientation du vecteur d'étirement dl→ qui donne la plus grande pente df/dl.
Et nous savons que :
- la norme de dl→ vaut :
dl = √(dx2 + dy2) (51) - df = f(x+dx,y+dy) - f(x,y)
Cependant, maximiser
[ ( x + dx ) * ( y + dy ) - x * y ] / √(dx2 + dy2)
est assez complexe.
Une voie plus simple consiste à exploiter le fait que
df = f(x+dx,y+dy) - f(x,y)
est assez proche de la définition de la dérivée
df / dx = ( f(x+dx) - f(x) ) / dx (81).
En effet, pour passer de la première à la seconde, il suffit de supprimer la variable y (ou x), et de diviser les deux membres par dx (ou dy).
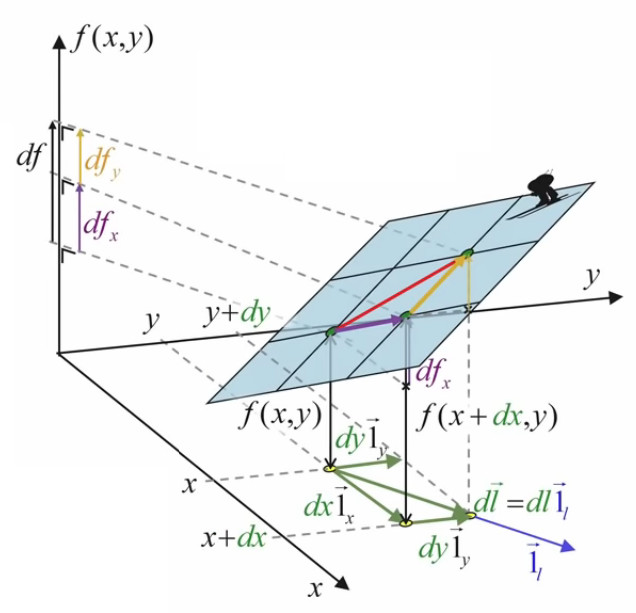
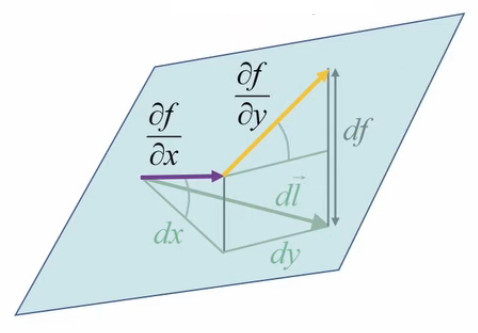
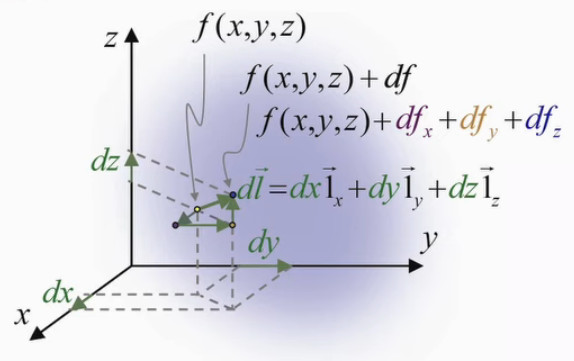
Alors bien sûr df / dx (ou df / dy) n'est pas df / dl. Cependant le passage à l'approche infinitésimale a pour effet qu'à un segment infinitésimal dl, correspond sur la surface quelconque (courbe) f(x,y) une surface de l'on peut considérer comme plane :
Or, dans ce contexte de surface plane, le graphique suivant illustre que la différentielle totale de f est égale à la somme de ses différentielles partielles :
df = dfx +dfy ⇔
df = f(x+dx,y) - f(x,y) + f(x,y+dy) - f(x,y)
Le graphique ci-dessous illustre la simplification du calcul apportée par l'approche infinitésimale conduisant à une surface plane : le vecteur orange (correspondant à dfy), dont l'origine était celle du vecteur violet, peut être translaté à la suite de celui-ci.
Pour formuler cette propriété, procédons à l'artifice mathématique suivant :
df = ( f(x+dx,y) - f(x,y) ) * dx / dx + ( f(x,y+dy) - f(x,y) ) * dy / dy
⇒ soit :
∂f/∂x =( f(x+dx,y) - f(x,y) ) / dx
la "dérivée partielle de f en x" (NB : ∂, appelé "d ronde", remplace les d).
Soit par exemple f(x,y)=2*x2*y3 ⇒ ∂f/∂x=4*x*y3 ⇒ au point par exemple (x,y)=(3,1) on a que ∂f/∂x=12.
que l'on substitue dans l'égalité précédente ⇒
df = ∂f/∂x * dx + ∂f/∂y * dy
... dont le membre de droite ressemble à la formulation algébrique du produit scalaire :
ax * dx + ay * dy = a→ . dl→ (59)
Pour que cette ressemblance devienne équivalence, il suffit de définir a→ tel que :
a→ = ∂f/∂x * 1x→ + ∂f/∂y * 1y→ = ∇→f
qui est appelé "gradient" de la fonction f (et noté ∇→f plutôt que a→), et qui est donc « le vecteur dont les composantes en x et y sont les dérivées partielles de f en x et y (c-à-d les pentes de f en x et y) »
⇒ il résulte de (93) et (92) que
df = ∂f/∂x * dx + ∂f/∂y * dy = ∇→f . dl→
c-à-d que le différentiel total d'une fonction de plusieurs variables est égal au produit scalaire du vecteur déplacement dl→ par le vecteur gradient ∇→f (et le produit scalaire est la somme des produit des composantes homologues).
N.d.A. Le développement ci-dessus peut également se faire comme suit :
pour exprimer :
df = ∂f/∂x * dx + ∂f/∂y * dy (92)
en fonction de :
dl→ = ( dx , dy ) = dx * 1x→ + dy * 1y→ (56)
il suffit de définir :
∇→f = ∂f/∂x * 1x→ + ∂f/∂y * 1y→
(93)
de sorte que :
df = ∂f/∂x * dx + ∂f/∂y * dy = ∇→f . dl→
(94)
Le symbole ∇ est appelé "nabla" (nom grec d'une petite harpe).
Le graphique suivant illustre précisément les composantes de la différentielle totale df (94) :- à la différentielle partielle dfx correspond l'angle formé par la composante mauve avec dx
- à la différentielle partielle dfy correspond l'angle formé par la composante jaune avec dy
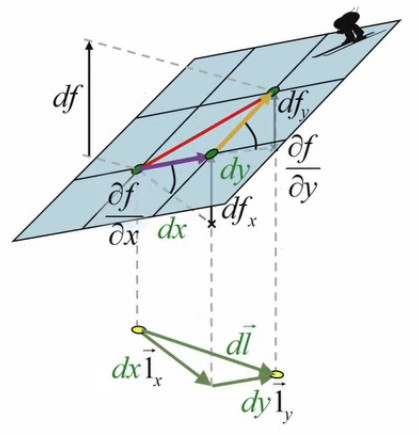
Nous approchons de la solution puisque nous avons maintenant une relation entre df et dl→. Mais notre objectif est de formuler la relation entre df et dl, et plus précisément de déterminer l'orientation du vecteur d'étirement dl→ qui donne la plus grande pente df/dl. Pour ce faire il suffit de diviser par dl (module de dl→) les deux membres de (94) :
df / dl = ∇→f . dl→ / dl ⇔
df / dl = ∇→f . dl * 1→l / dl ⇔
df / dl = ∇→f . 1→l
df / dl est appelée "dérivée directionnelle" de la fonction f, dans la direction 1→l du déplacement dl. Le terme "dérivée" est quelque peu abusif car l n'est pas une variable de f, mais il se justifie par le fait que df / dl est la pente de la fonction f dans une direction donnée 1→l.
En effet, par (58), on a alors que :
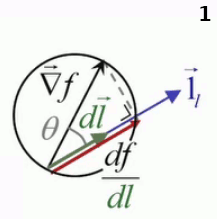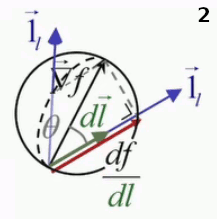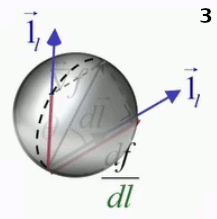
df / dl = ||∇→f|| * ||1→l|| * cosθ ⇔
df / dl = ||∇→f|| * cosθ
où θ est l'angle entre ∇→f et 1→l
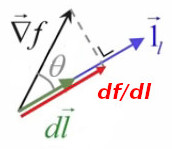
Le terme "directionnelle" n'est donc quant à lui pas du tout abusif : il signifie que la variation de f dépend du module dl du vecteur déplacement dans une direction donnée 1→l.
Le graphique suivant permet de situer en 3D le graphique précédent : df/dl c-à-d la pente de f le long de dl, c-à-d la tangente de l'angle entre cette pente de f et dl, c'est la projection du gradient ∇→f sur la direction 1→l du déplacement.
Nous pouvons maintenant résoudre notre problème de maximisation de df/dl en modulant l'orientation : df/dl, c-à-d la projection du gradient dans la direction du déplacement dl→, est à son maximum lorsque la direction du déplacement est celle (c-à-d parallèle à celle) du gradient ∇→f ! En effet, dans ce cas θ=0 ⇒ cosθ est alors à sa valeur maximale de 1 ⇒
df / dl |max = ||∇→f ||

On voit ainsi que le gradient est un vecteur qui permet de caractériser les variations de la fonction :
- il indique la direction de plus grande pente ;
- son module est la valeur cette plus grande pente.
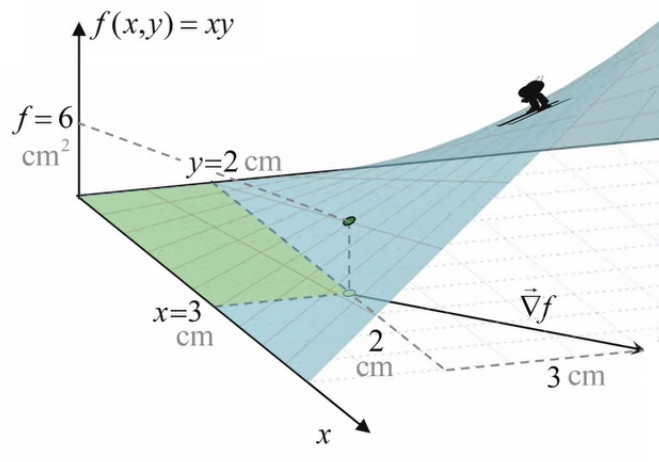
Nous allons maintenant résoudre notre problème d'optimisation à partir du cas concret d'un rectangle déterminé par le point (3,2), et dont la surface f vaut donc 3*2=6cm2.
∇→f = ∂f/∂x * 1x→ + ∂f/∂y * 1y→ (93) ⇒
puisque f(x,y) = x * y ⇒
∇→f = y * 1x→ + x * 1y→ ⇒
∇→f(3,2) = 2 * 1x→ + 3 * 1y→ [cm] ⇒
Commençons par calculer la dérivée directionnelle (qui est une pente), correspondant à un angle α quelconque (mesuré par rapport à l'axe x).
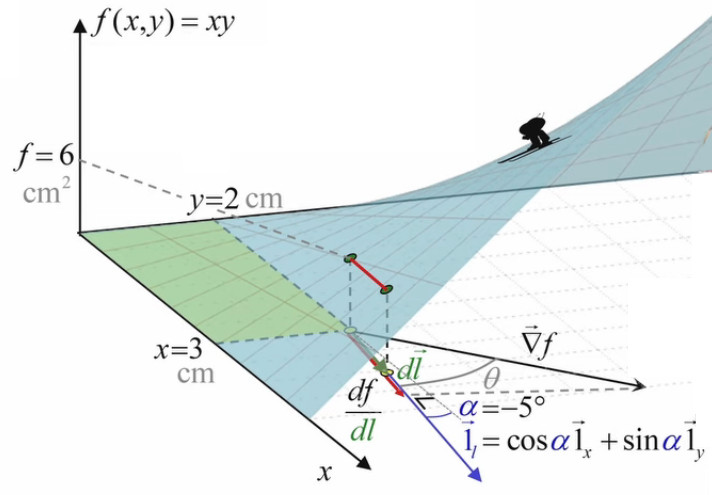
df / dl = ∇→f . 1→l
(95)
Or :
• ∇→f(3,2) = 2 * 1x→ + 3 * 1y→
• 1→l = cos(α) * 1→x + sin(α) * 1→y
⇒ par (59) :
df / dl = 2 * cos(α) + 3 * sin(α)
ainsi dans le graphique ci-dessus, dl→ à été dessiné sur une angle arbitraire de α = -5°, ce qui correspond à une pente df / dl = 1,73 cm.
La valeur de la pente maximale quant à elle correspond à θ=0 ⇒
df / dl |max = ||∇→f|| * cos0 (96) ⇒
df / dl |max = ||∇→f|| ⇔
df / dl |max = √(22 + 32) = 3,6 cm
Calculons enfin l'orientation du gradient correspondant à cette pente maximale (graphique suivant : angle γ par rapport à l'axe x, à ne pas confondre avec l'angle θ que forme le vecteur d'étirement par rapport au gradient) :
tg(γ) = 3/2 ⇔
γ = arctan(3/2) ≈ 56°

O peut généraliser la résolution du problème au cas de n'importe quel rectangle :
∇→f(x,y) = y * 1x→ + x * 1y→ [cm]
- dont le module vaut : df / dl |max = ||∇→f || = √(y2 + x2) cm
- dont l'angle par rapport à l'axe x vaut : γ = arctan(x/y)
Champ vectoriel. À noter que, dès lors que l'on peut définir le vecteur gradient en tout point du domaine de définition de la fonction f(x,y), on peut donc considérer que le gradient d'une fonction scalaire est un champ vectoriel. Celui-ci donne des informations sur la façon dont la fonction varie.
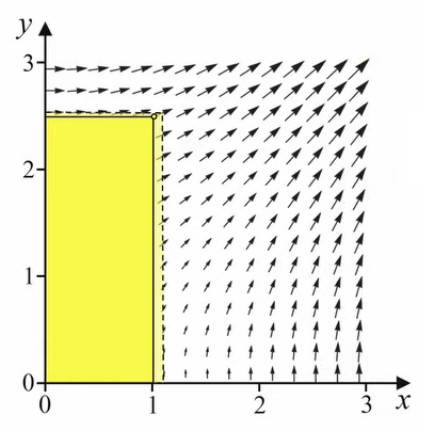
On constate que l'orientation des vecteurs gradients est inférieure à 45°, ce qui est intuitif : on maximise évidemment la surface en tirant plus du côté le plus long. Selon le même raisonnement, les gradients situés sur l'axe à 45° correspondent au carré. On notera que cette intuitivité de la solution n'est plus apparente pour des problèmes plus complexes, et c'est évidemment dans ces cas là que l'outil mathématique du gradient s'avère particulièrement utile.
Nous allons ici montrer que la notion de gradient s'applique directement à celle de ligne de niveau, qui est une coupe horizontale du relief, et dont tous les points du périmètre de base représentent une même hauteur par rapport au niveau de la mer.
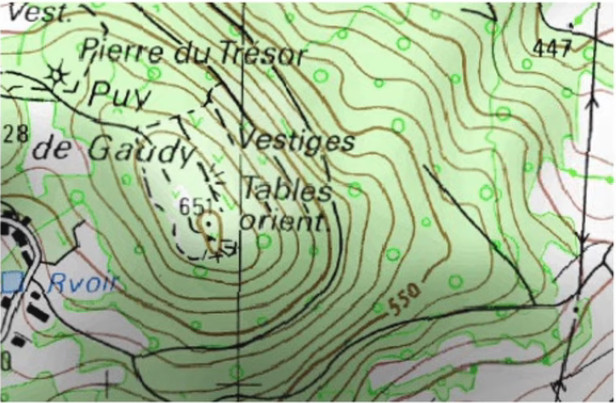
Le principe de lecture d'une telle carte est donc que plus on se déplace parallèlement aux lignes, plus le relief du trajet est plat, et plus on se déplace perpendiculairement aux lignes, plus le trajet est pentu. C'est évidemment via la notion de pente que le lien avec le gradient apparaît.
Formalisation. Le relief de la Terre peut être représenté par une fonction "altitude" : à chaque point de longitude x et latitude y, correspond une altitude h(x,y). Ainsi une ligne de niveau est telle que h(x,y) = k où k est l'altitude de chaque point de la ligne.
Comprenons bien que cette notion de courbe de niveau peut être généralisé à toute fonction de deux variables, comme par exemple T = P * V / N / kB (190), ou encore notre exemple précédent h = x * y. L'unité de la fonction T=f(P,V) est l'unité de température (degré Celsius ou Kelvin), et l'on parle de ligne isotherme, tandis que l'unité de la fonction h(x,y) est l'unité de surface (m2).
Nous avons déjà vu que dans ce second cas la fonction prend elle-même la forme d'une surface (représentée en bleu). En chaque point de celle-ci la valeur de la fonction exprime la surface du rectangle jaune (et non pas une hauteur physique). La direction du gradient indique la direction de plus grande pente de la fonction. C'est cette direction qu'il faut suivre pour faire varier au maximum la surface jaune f(x,y).
À la surface de f(x,y) on peut associer une série de lignes de niveau. Les points d'une même ligne correspondent à une série de rectangles de même surface jaune.
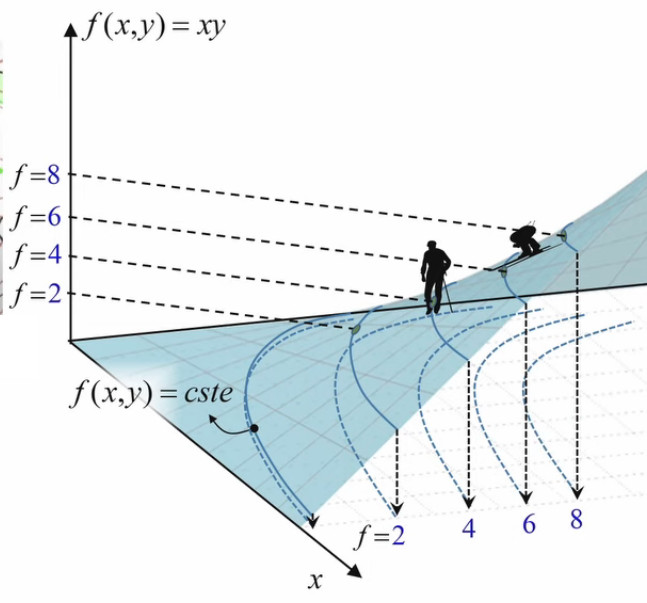
La représentation bidimensionnelle est plus simple que la représentation tridimensionnelle. On y voit ici une série de rectangles jaunes correspondant à une même surface f(x,y)=2.
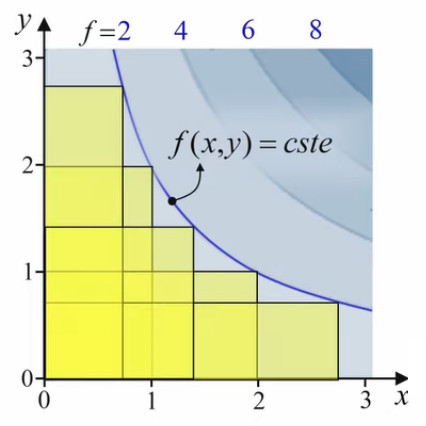
On peut y représenter les vecteurs gradients. À noter que dans le graphique ci-contre l'échelle du module de ∇→f = ∂f/∂x * 1x→ + ∂f/∂y * 1y→ (93) est réduite (1 cm devrait correspondre à la distance unitaire des axes) afin de pouvoir en représenter clairement un grand nombre.
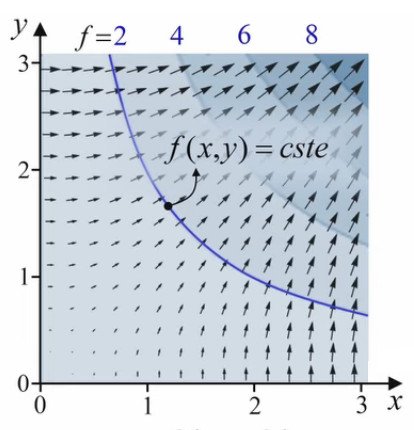
Comprenons bien le lien entre gradient et ligne de niveau. Le gradient exprime la variation de la fonction f, qui est donnée par df = ∇→f . dl→ (94) où dl→ = dx * 1x→ + dy * 1y→ "cache" les variations dx et dx des variables x et y de la fonction.
Le graphique ci-contre nous rappelle la signification géométrique de ce produit scalaire ∇→f . dl→ = ∂f/∂x * dx + ∂f/∂y * dy (94) : df, la variation totale de la fonction f(x,y) sous l'effet de variations dx et dy (symbolisées par le vecteur dl→), est donnée par la pente en x fois dx, plus la pente en y fois dy.
Cette interprétation géométrique étant rappelée on comprend alors toute la puissance de df = ∇→f . dl→ pour formuler un déplacement le long d'une ligne de niveau : on l'exprime tout simplement par df = ∇→f . dl→ = 0. Or nous savons qu'un produit scalaire nulle exprime le fait que les vecteurs ∇→f et dl→ sont perpendiculaires (cf. supra #produit-scalaire). Ainsi dans le graphique supra montrant le champ de gradients, ceux-ci sont perpendiculaires à chaque courbe de niveau qu'ils croisent.
De même, la dérivée directionnelle df / dl = ||∇→f|| * cosθ = 0 (96) correspond à θ=π/2, où θ est l'angle entre vecteurs radient et direction.
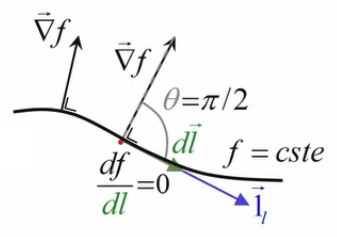
Voici donc clairement illustré le lien entre gradient et ligne de niveau. On constate ici toute la puissance mathématique de la notion de gradient, sans laquelle on aurait que df = ∂f/∂x * dx + ∂f/∂y * dy = 0 (94) pour formuler le déplacement le long d'une ligne de niveau.
Lignes
de champ
Le gradient est un champ vectoriel qui est partout perpendiculaire aux lignes de niveau (bleues). On peut alors introduire la notion de lignes de champ (noires), qui en tout point sont tangentes au champ de gradients. Ainsi un déplacement sur une ligne de champ correspond à une déplacement de pente maximale, tandis que les déplacement sur une ligne de niveau correspond à une déplacement de pente nulle.
Notons d'autre part que les lignes de niveau apportent une information sur le module du gradient, de sorte que l'on n'est plus obligé de représenter l'ensemble des vecteurs dont le module augmentent vers le nord-est. En effet dès lors que les lignes de niveau dessinées correspondent à un même incrément de la fonction, on en déduit que des lignes plus espacées correspondent à une pente plus faible, et inversement. Ainsi dans le graphique l'espace entre les lignes de niveau diminue lorsqu'on se déplace vers le nord-est.
Sur base de ce que nous avons développé supra, la pente que gravit le montagnard dans son trajet sinueux est donnée par la dérivée directionnelle de la fonction "altitude" f(x,y), où x et y déterminent la position du marcheur par ses longitude et latitude. Cette dérivée directionnelle vaut le produit scalaire du gradient de la fonction (donnant la direction de plus grande pente) et du vecteur unitaire dans la direction du déplacement : df / dl = ∇→f . 1→l (95). L'angle θ entre le vecteur gradient et la direction du déplacement conditionne la valeur du taux de variation de la fonction altitude : df / dl = ||∇→f|| * cosθ (96).
Nous avons vu également que le vecteur gradient ∇→f = ∂f/∂x * 1x→ + ∂f/∂y * 1y→ (93) peut être représenté graphiquement par le "champ gradient de la fonction". Nous allons présenter ici une façon de représenter, pour un point donné de ce champ, l'ensemble des valeurs prises par le taux de variation df/dl en fonction de la direction.
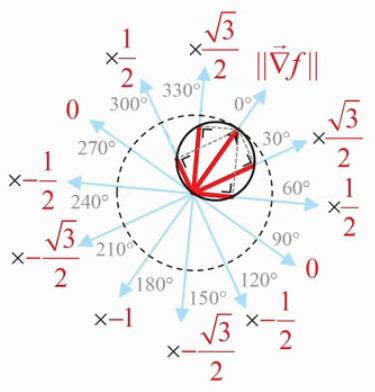
Voici quelques-une de ces valeurs :
- si la direction est celle du gradient ⇔ θ=0 ⇒ df/dl = ||∇→f || (NB : en l'occurrence il s'agit de la valeur maximale de cette pente) ;
- si la direction est orthogonale au gradient ⇔ θ=π/2 ⇒ df/dl = 0 (NB : en l'occurrence il s'agit de la valeur d'une courbe de niveau) ;
- si la direction est de 30° par rapport au gradient ⇔ θ=30° ⇒ df/dl = ||∇→f || * √(3)/2 (NB : ainsi en déviant de 30% par rapport à la direction de plus grande pente on est encore à environ 87% de celle-ci...) ;
- si θ=60° ⇒ df/dl = ||∇→f || * 1/2 ;
- si θ=120° ⇒ df/dl = ||∇→f || * -1/2 (NB : on descend sur une pente valant la moitié de la pente maximale) ;
- si θ=180° ⇒ df/dl = ||∇→f || * -1 (NB : on descend sur la pente maximale) ; ... etc
Dans le graphique suivant les traits rouges représentent les valeurs de df/dl pour θ valant 0°, 30°, 60°, 300° et 330°. On notera que cette étoile "cannabis" s'incrit dans un cercle, dont le diamètre vaut le gradient et passant par le point auquel on étude les variations de la fonction f(x,y) en fonction de la direction.
En effet on peut démontrer que tous les triangles rectangles ayant la même hypoténuse on leur sommet sur un cercle dont le diamètre est cette hypoténuse. Il résulte de cette propriété que la projection orthogonale du gradient sur une direction déterminée, c-à-d la la dérivée directionnelle de f(x,y), est la longueur de la direction intérieure au cercle.
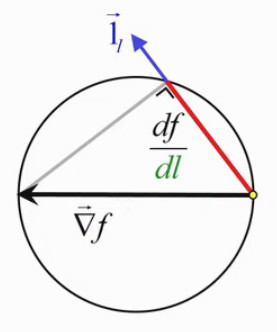
On peut alors, dans le graphique du champ de gradient, remplacer le vecteur gradient par l'étoile "cannabis", pour symboliser de façon plus complète et intuitive l'information contenue dans le concept de gradient. Dans le graphique ci-contre la direction sort du cercle ⇔ on a donc une valeur négative de la pente df/dl ⇔ dans cette direction, la valeur de la fonction diminue.
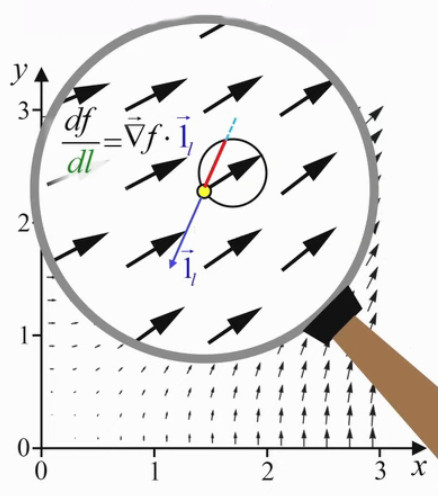
L'image suivante illustre l'application de ce principe à notre montagnard.
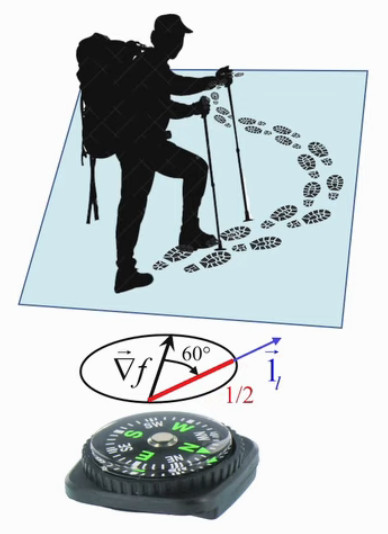
Les sept premières minutes de cette vidéo rappellent l'essentiel de la première des cinq vidéos consacrées au gradient : celui-ci a été défini de telle sorte qu'il permet d'exprimer df en fonction du vecteur déplacement dl→ ⇒ en divisant les deux membres de cette expression par dl on obtient la dérivée directionnelle c-à-d la pente df/dl.
Dans cette dernière vidéo consacrée au gradient on souligne le fait que l’expression mathématique de la dérivée directionnelle en termes de gradient ne dépend pas du nombre de variables de la fonction.
Ainsi en 3D, on ajoute simplement une troisième composante (z), de sorte que le développement de (92) à (94) devient que, pour exprimer :
df = ∂f/∂x * dx + ∂f/∂y * dy + ∂f/∂z * dz (92)'
en fonction de :
dl→ = ( dx , dy , dz) = dx * 1x→ + dy * 1y→ + dz * 1z→ '
il suffit de définir :
∇→f = ∂f/∂x * 1x→ + ∂f/∂y * 1y→ + ∂f/∂z * 1z→
(93)'
de sorte que :
df = ∂f/∂x * dx + ∂f/∂y * dy + ∂f/∂z * dz = ∇→f . dl→ (94)'
⇔
df /dl = ∇→f . dl→ / dl
⇔
df /dl = ∇→f . 1→l (95)
qui est effectivement identique au cas à deux dimensions. CQFD.
La trajectoire dl→ est décomposée en trois composantes dx, dy et dz.
Une différence apparaît cependant dans la représentation graphique du gradient, exposée dans la vidéo précédente. À deux dimensions, la projection orthogonale du gradient sur une direction déterminée – c-à-d la la dérivée directionnelle de f(x,y) – est la longueur de la direction intérieure au cercle dont le diamètre vaut le gradient et passant par le point auquel on étude les variations de la fonction f(x,y) en fonction de la direction.
Mais en 3D, le vecteur direction peut être pris dans n'importe quelle direction par rapport au gradient, et à chacune de ces directions correspond un cercle passant par le point déterminé par la projection du gradient sur le vecteur direction et leur point d'application commun, de sorte que la méthode du cercle en 2D devient en 3D la "méthode de la sphère", où la dérivée directionnelle a pour valeur la longueur du segment intérieur à la sphère, dans la direction du déplacement.
Animation en trois images montrant le passage de l'interprétation graphique 2D à 3D. Le second vecteur direction, apparaissant à l'image 2, sort du plan et détermine un autre cercle passant par le même point d'application des vecteurs gradient et direction.
Ainsi l'analogie botanique avec la feuille de canabis – dont les doigts indiquent que la dérivée directionnelle est la plus grande dans le sens du gradient, et diminue au plus la direction se rapproche de l'orthogonalité au gradient – pourrait être prolongée en 3D par l'analogie avec une fleur de trèfle, constituée de jets qui partent tous du même point.
Nous sommes maintenant en mesure d'étudier les phénomènes de propagations dans les quatre exemples illustrés au début de la première vidéo. On notera que le quatrième exemple, une algorithme d'optimisation, est applicable à des fonctions composées de (beaucoup) plus de trois variables, ce qui est particulièrement utile dans le domaine de l'IA.
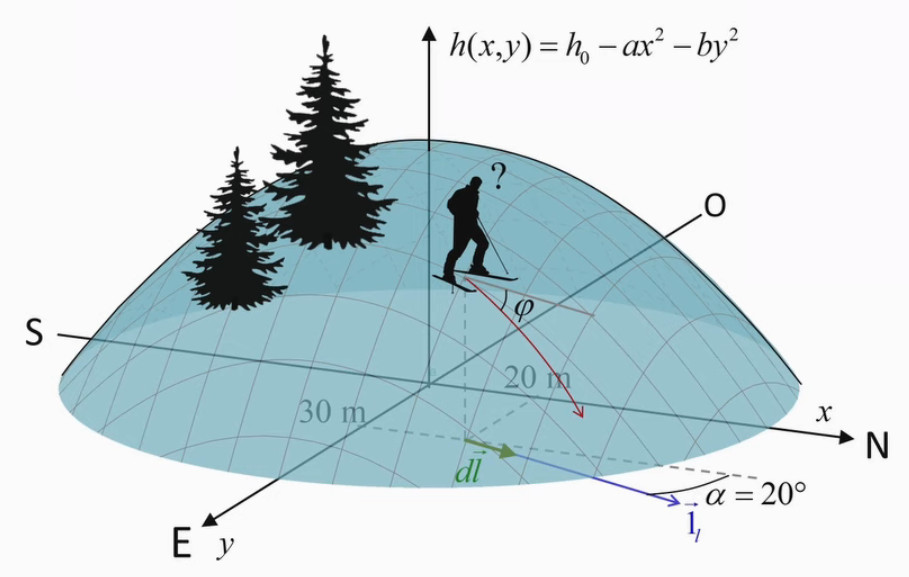
Soit une montagne telle que :
- modélisée mathématiquement au moyen de la fonction altitude h(x,y) où x et y sont les coordonnées de la position du skieur repérée sur le plan XY (NdA : du niveau de la mer), dont l'origine correspond au sommet de la montagne ;
- les axes X et Y correspondent à la latitude (S→N) et longitude (O→E) mais sont mesurés en mètres relativement à l'origine des axes X et Y, plutôt qu'en degrés relativement au croisement de l'équateur et du méridien de Greenwich.
Quelle est la pente φ prise par un skieur étant donné que ? :
- il se dirige vers le cap 20° NNE ;
- le skieur est positionné au point (x,y)=(20,30), l'unité valant 10 mètres ;
- la forme de la montagne est modélisée au moyen d'un paraboloïde (une parabole en X et une parabole en Y) h(x,y) = h0 - a * x2 - b * y2 où :
- h0 = 710m est la hauteur de la montagne (belge...), qui est bien la valeur de h(0,0);
- a = 15 10-3 m-1
- b = 12 10-3 m-1
On a bien ainsi que h est mesurée en mètres : m - m-1 * m2 - m-1 * m2 ≡ m
Résolution
Il nous est demandé de calculer une pente, c-à-d une dérivée, étant donné que la direction est connue. L'outil mathématique dont nous avons besoin est donc la dérivée directionnelle. Et nous disposons des données requises pour la calculer, dont une direction (20°) à partir d'une position (20,30).
Le système d'équation de la solution est donc :
dh / dl = tg(φ)
(90)
dh / dl = ∇→h . 1→l
(95)
∇→h = ∂h/∂x * 1x→ + ∂h/∂y * 1y→
(93)
1l→ = cos(α) * 1x→ + sin(α) * 1y→
(89)
Par (90) on voit que l'angle φ est donné par la dérivée directionnelle, laquelle se calcule par (95) c-à-d le produit scalaire du gradient calculé par (93) et du vecteur unitaire directionnel calculé par (89) :
(93) : ∇→h = - 2 * a * x * 1x→ - 2 * b * y * 1y→
(89) : 1l→ = cos(α) * 1x→ + sin(α) * 1y→
Par et
(59) on sait que la valeur du produit scalaire (95) sera donc :
-2 * a * x * cos(α) - 2 * b * y * sin(α) ⇒
tg(φ) = -2 * a * x * cos(α) - 2 * b * y * sin(α) ⇒
tg(φ) = -2 * 15 10-3 * 20 * cos(20) - 2 * 12 10-3 * 30 *sin(20) ⇒
tg(φ) ≈ -0,81 ⇒
φ = -39°
Pour terminer interprétons rapidement le second des quatre exemples illustrés au début de la première des vidéos consacrées au gradient.

J→ = - kT * ∇→T Notre équation de conduction thermique exprime que le flux de chaleur est proportionnel (kT est le coefficient de conductivité thermique) à l'opposé du gradient, c-à-d qu'il se dirige dans le sens opposé au gradient. Celui-ci est visible par le gradient des couleurs : du blanc (au centre, plus chaud) vers le rouge (aux extrêmes, moins chaud). Rappel : nous avons vu que le gradient est perpendiculaire aux courbes de niveau.
Voilà qui termine la série des (six) vidéos sur le gradient et la dérivée directionnelle.
Intégrale
2. Pratique du calcul intégral
Théorie du calcul intégral
Dans la section consacrée à la dérivée nous avons vu que "dériver" (par rapport au temps) consiste à calculer le taux de variation v(t) = dx(t) / dt à partir de la variation dx(t). L'opération inverse, c-à-d calculer la variation à partir du taux de variation, s'appelle "intégrer" : Δx(t) = ∫ dx(t) = ∫ v(t) * dt.
Pour ce faire l'équation xt - x0 = v * t (162) du MRU suffit certes, car v est constant. Mais si le taux de variation est variable (cas du MRUA) alors on devra utiliser un nouvel outil mathématique : l'intégrale.
Le principe de l'intégrale consiste à découper le temps en tranches et d'attribuer à chacune une vitesse constante qui n'est autre que la vitesse moyenne de cette tranche. Nous avons vu dans l'illustration du MRU (162) que la surface du rectangle correspondant est précisément la variation que l'on souhaite retrouver (en l'occurrence la distance parcourue).
Dès lors pour affiner l'intégration on passe d'un nombre fini de tranches (graphique de gauche ci-dessous, où elles sont notées en Δ) à un nombre infini de tranches infinitésimales (graphique de droite, où elles sont notées en d). Ce faisant on remplace la fonction discontinue vn = Δxn / Δt par la fonction continue v(t) = dx(t) / dt.

La flèche verte représente la fonction d'intégration (la flèche inverse représente donc la fonction de dérivation). Le graphique de droite représente la notation spécifique de l'intégrale, et sa signification géométrique d'effet de lissage.
Maintenant que nous avons exposé la signification géométrique d'une intégrale nous allons voir comment la calculer. Mais pour cela il nous faut d'abord transformer le résultat du graphique de droite ci-dessus en une fonction du temps c-à-d que l'on considère x( tf ) comme variable de sorte que l'on remplace x( tf ) par x( t ), et que x( ti ) est considéré comme connu (et passe donc dans le membre de droite ⇒ la flèche verticale bleu descend maintenant jusqu'à l'origine de l'axe x(t) ).
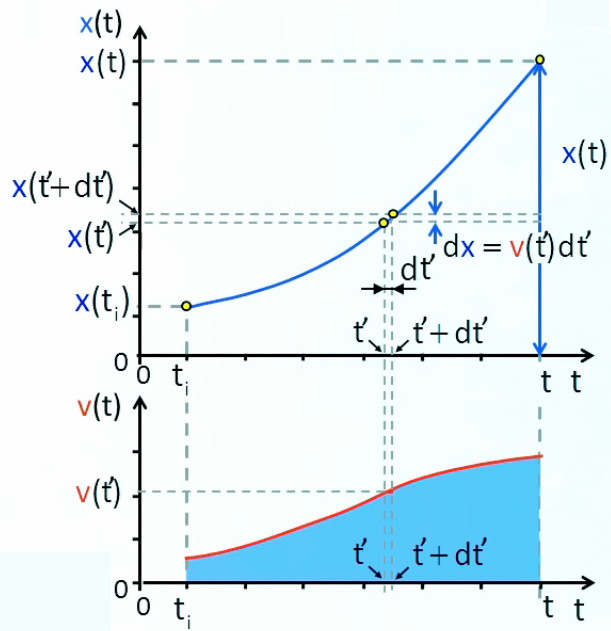
Il nous faut également distinguer le t de la variable du t représentant la borne finale de l'intégrale ⇒ on remplace le premier par t' (qui représente le temps passé).
Après ces corrections de notations on obtient : x(t) = x(t i) + ∫ t it v(t') * dt'
Le calcul d'une intégrale se résume alors en un règle simple : « l'intégrale de f(x) est la différence des primitives de f(x) entre les bornes » :
∫ x ix f f(x) * dx = F(xf) - F(xi)
que l'on note aussi :
∫ x ix f f(x) * dx = [ F(x) ] x ix f
où F(x) est appelée "primitive" de "l'intégrande" f(x), et est telle que
F(x) = ∫ f(x) * dx ⇔ dF(x) / dx = f(x)
NB : primitive et dérivée sont donc des fonctions inverses.
Pour montrer le raisonnement conduisant à (98) on part de
x(t) = x(ti) + ∫ t it v(t') * dt'
(97)
appliquée au MRU c-à-d telle que v(t')=v0
Or dans ce cas on sait que la solution est x(t) = v0 * t + x0 (162)
qui vaut aussi pour x(ti) = v0 * ti + x0
que l'on substitue dans (97) ⇒
∫ t it v(t') * dt' = v0 * t - v0 * ti
Comme on est dans le cas v(t')=v0 ⇒ on vérifie bien que :
∫ t it v0 * dt' = v0 * ( t - ti ) ⇔
v0 * ∫ t it dt' = v0 * ( t - ti ) ⇔
v0 * ( t - ti ) = v0 * ( t - ti )
Ce résultat obtenu pour v(t')=v0 on le généralise à toute fonction v(t') en posant
∫ t it v(t') * dt' = V(t) - V(ti )
où V(t) est telle que dV(t) / dt = v(t')
On peut alors démontrer formellement (98) en partant de la primitive
V(t) = ∫ t*t v(t') * dt' + C ⇔
V(t) = ∫ t*ti v(t') * dt' + ∫ ti t v(t') * dt' + C ⇔
V(t) = V(ti) - C + ∫ ti t v(t') * dt' + C ⇔
∫ ti tv(t') * dt' = V(t) - V(ti)
CQFD
La principale difficulté du calcul d'une intégrale consiste donc en l'identification de la primitive de l'intégrande. Cette maîtrise vient par la pratique de l'intégration et la mémorisation de primitives fréquentes.
Quelques primitives fréquentes
| Intégrande f(x) | Primitive F(x) |
|---|---|
| 1 / x | ln(x) |
| 1 / x2 | - 1 / x |
| sin(x) | - cos(x) |
| cos(x) | sin(x) |
La primitive est l'intégrale de l'intégrande, à une constante près. L'intégrande est la dérivée de la primitive.
Nous avons vu supra que dès l'antiquité on a pu calculer la surface du cercle par la méthode de décomposition infinitésimale, qui consiste à sommer un nombre infiniment grand de grandeurs infiniment petites (#calcul-infinitesimal). Cette méthode conduira, deux mille ans plus tard (au 17° siècle), à la notion d'intégrale (ou "opération d'intégration"), et plus généralement au calcul différentiel et au calcul intégral, grâce aux travaux des mathématiciens Newton et/ou Leibniz.
Pour calculer la surface du cercle dont le rayon R est connu, les savants de l'antiquité avaient conçu une méthode consistant à diviser le cercle en un grand nombre N de triangles (de surface ST dans le développement ci-dessous) composant un polygone inscrit dans ce cercle. La surface S du cercle est alors approchée par celle du polygone :
SP = N * ST ⇒ par (19) :
SP = N * base * R / 2 ⇔
SP ≈ N * circonférence / N * R / 2 ⇒ par (25) :
SP ≈ N * 2 * π * R / N * R / 2
SP ≈ π * R2 = S (27)
L'indétermination ∞ * 0 (cf. première égalité : un nombre N infiniment grand de surfaces infiniment petites ST) est résolue par le passage entre la deuxième égalité (stricte) et l'équivalence suivante (induite par circonférence ≈ N * base), dès lors que cette indétermination devient une équivalence à l'unité :
∞ * 0 ≈ N * 1 / N = 1
Le problème de l'indétermination ∞ * 0 a donc été résolu ... sans devoir utiliser le calcul intégral.
Mais nous allons montrer que la méthode de décomposition infinitésimale conduit en toute généralité à la notion d'intégrale. Pour ce faire non allons décomposer le cercle, non plus en triangles identiques (qui posent le problème de l'approximation) mais en bandes circulaires (anneaux) correspondant à autant de cercles concentriques de rayon variable r (lequel est appelé "variable d'intégration"), entre r0=0 et rN=R (R étant le rayon du cercle dont on cherche la surface). L'idée est ici que la surface du cercle est (cette fois exactement) la somme de la surface des anneaux. Nous allons voir que la problématique d'approximation est alors ramenée dans le calcul de la surface de l'anneau.
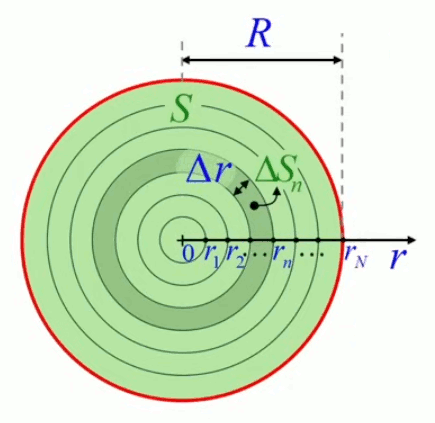
La variable d'intégration r va nous permettre de formuler mathématiquement la notion de décomposition infinitésimale, via Δr qui est la différence – constante – entre rayons ri et ri+1 de deux cercles consécutifs. Cette différence (dont la notation deviendra "différentielle") entre deux valeurs consécutives de la variable d'intégration r est telle que :
R = N * Δr
rn = n * Δr où n=1,2,3,...,N.
de sorte que rN = R, rayon du cercle SN.
Et la surface du cercle est la somme des N anneaux ΔSn :
S = ∑i=1NΔSn
Pour calculer ΔSn nous allons faire appel à notre connaissance de la formule de la surface du cercle. Cela relève certes du raisonnement circulaire, mais notre objectif n'est pas ici de démontrer à nouveau (27). C'est plutôt de montrer, via le cas de la surface du cercle, que la décomposition infinitésimale conduit à la notion d'intégrale.
Pour ce faire on va exploiter le fait que :
ΔSn = Sn - Sn-1 ⇔
ΔSn = π * rn2 - π * rn-12 ⇔
ΔSn = π * ( rn-1 + Δr ) 2 - π * rn-12 ⇔
ΔSn = π * rn-12 + 2 * π * rn-1 * Δr + π * Δr2 - π * rn-12 ⇔
ΔSn = 2 * π * rn-1 * Δr + π * Δr2
Pour analyser ce résultat, on va supposer qu'un anneau est composé d'une corde enroulée. Si l'on coupe l'anneau à la fin de la corde (cf. trait noir horizontal dans le schéma ci-dessous), il est alors assez intuitif que l'on obtient un série de corde dont la taille croît linéairement, puisque la circonférence est proportionnelle au rayon, selon la croissance différentielle de :
2 * π * rn-1
à
2 * π * rn = 2 * π * ( rn-1 + Δr ) = 2 * π * rn-1 + 2 * π * Δr
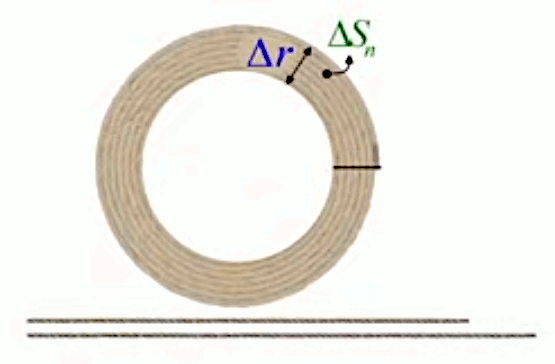
Il est alors aussi intuitif que la surface de l'anneau vaut celle du trapèze formé par les cordes.

Et l'on constate que la surface du trapèze correspond bien à l'expression de :
ΔSn = ΔSn = 2 * π * rn-1 * Δr + π * Δr2 (100).
Observons la pointe de ce trapèze : il s'agit d'un triangle (cf. illustration ci-dessous) :
• de hauteur = base sup. du trapèze - base inf. du trapèze = 2 * π * Δr
• de base = Δr
et dont par conséquent la surface vaut :
Δr * ( 2 * π * Δr ) / 2 = π * Δr2
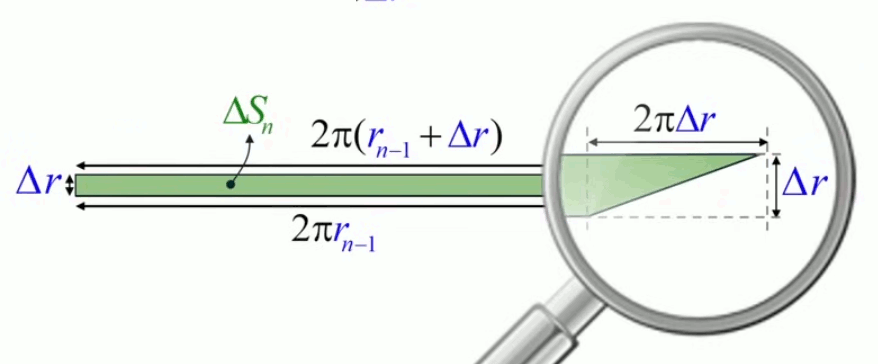
Et on constate que la surface de ce triangle constitue le dernier élément de :
ΔSn = 2 * π * rn-1 * Δr + π * Δr2 (100).
qui est donc composée d'une partie rectangulaire et d'une partie triangulaire.

L'étape suivante consiste à injecter cette valeur de ΔSn dans :
S = ∑n=1N ΔSn ⇒
S = ∑i=1N ( 2 * π * rn-1 * Δr + π * Δr2 ) ⇔
S = ∑n=1N 2 * π * rn-1 * Δr + ∑i=1N π * Δr2 ⇔
S = ∑n=1N 2 * π * rn-1 * Δr + N * π * Δr 2 ⇔ par (99) :
S = ∑n=1N 2 * π * rn-1 * Δr + N * π * ( R / N )2 ⇔
S = ∑n=1N 2 * π * rn-1 * Δr + π * R 2 / N ⇔
... dont le dernier terme (la surface du petit triangle du schéma supra) tend vers zéro lorsque N tend vers l'infini.
On peut d'ailleurs généraliser que « toute expression contenant la différentielle de la variable d'intégration à une puissance supérieure à 1 peut être considérée comme négligeable ». La raison de cette particularité – propre au calcul infinitésimal – apparaît dans le passage à la dernière égalité : quand on fait une décomposition infinitésimale, on obtient N terme en 1 / N 2, soit un terme en 1 / N, qui tend vers zéro quand N tend vers l'infini.
N.d.A. L'autre terme du second membre de l'égalité supra ne tend pas vers zéro lorsqu'on y substitue (99). Pour le démontrer, constatons pour N=4 que :
∑n=1N 2 * π * rn-1 * R / N
devient :
2 * π * R / 4 * ( r0 + r1 + r2 + r3 ) =
2 * π * R / 4 * ( r0 + r0 + Δr + r0 + Δr + Δr + r0 + Δr + Δr + Δr ) =
2 * π * R / 4 * ( 4 * r0 + 6 * Δr ) =
que l'on peut généraliser, par (124), en :
2 * π * R / N * ( N * r0 + N * ( N - 1 ) / 2 * Δr ) =
2 * π * R / N * ( N * Δr + N * ( N - 1 ) / 2 * Δr ) =
2 * π * R * Δr / N * ( N + N * ( N - 1 ) / 2 ) =
2 * π * R * Δr / N * ( N + N2 / 2 - N / 2 ) =
2 * π * R * Δr * ( 1 + N / 2 - 1 / 2 ) =
(N.B. : N a disparu du dénominateur)
2 * π * R * Δr * ( N - 1 ) / 2 = (par (99) )
π * R2 / N * ( N - 1 ) =
π * R2 * ( 1 - 1 / N ) ≈ π * R2
lorsque N tend vers l'infini.
Rappelons que la présente démarche n'est pas ici de démontrer une n-ième fois la surface du cercle, mais d'illustrer le fait que celle-ci peut être calculée par le calcul intégral.
Le fait que l'on peut négliger la petite partie triangulaire de la partie droite du schéma supra montre que nous n'avions pas besoin de connaître la formule de la surface du cercle pour calculer ΔSn : sa surface peut être vue comme celle du rectangle subsistant : périmètre * différentielle d'intégration. Et c'est parce que Δr peut être arbitrairement petit que cette approximation est valable.
Notre problème se réduit donc maintenant à calculer la somme des composants infinitésimaux de la surface du cercle :
S = ∑n=1N→∞ΔSn = ∑n=1N→∞ 2 * π * rn-1 * Δr
Rappel : l'indice de rn-1 indique qu'il s'agit du rayon du cercle intérieur de la bande : cf. (98).
Pour résoudre ce problème, Leibniz a introduit une notation spécifique pour représenter la situation limite où :
N → ∞ ⇒ Δr = ( R / N ) → 0 ⇒ ΔSn = 2 * π * rn-1 * Δr → 0 :
- Δr devient dr = ( R / N→∞ )→0 et est appelée "différentielle de la variable d'intégration" ;
N.B. N → ∞ ≢ N = ∞ car :
• N → ∞ ⇒ ( R / N ) → 0
• N = ∞ ⇒ R / N = 0 - rn = n * Δr, variable discrète, devient devient la variable continue r. La disparition de l'indiçage signifie que l'on ne peut plus dénombrer les étapes de la décomposition.
"Frottement" théorique. Cette notion de continuité revient implicitement à considérer N comme infini, alors qu'il ne fait que s'en approcher ...
- ΔSn = 2 * π * rn-1 * Δr devient dS = 2 * π * r * dr
- ∑n=1N→∞ΔSn devient ∫ dS
Il reste à introduire les bornes de l'intégration de r = 0 jusqu'à r = R :
S(R) = ∫ dS = ∫0R 2 * π * r * dr
L'apparition de la borne supérieure implique, dans le premier membre de l'égalité, l'expression de S comme fonction de R.
Comme illustré ci-dessous, le calcul de l'intégrale formulée supra consiste à comparer la surface du cercle de rayon r, soit S(r), avec celle du cercle de rayon r+dr, soit S(r+dr).
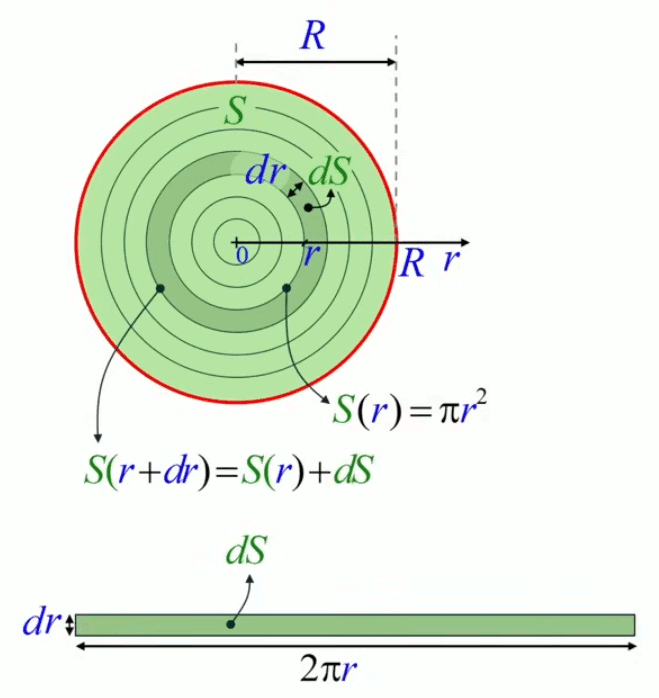
On a que :
S(r+dr) = S(r) + dS
c-à-d que la surface du grand cercle vaut celle du petit plus celle de l'anneau de surface dS, qui constitue la différence entre les deux cercles. On va ici la pertinence de la notation et nomenclature de Leibniz : dS est l'anneau différentiel. À partir de cette égalité géométrique, l'algèbre opère, et l'égalité peut s'exprimer comme :
S(r+dr) - S(r) = dS ⇔
( S(r+dr) - S(r) ) / dr = dS / dr
NB : dS est fonction de dr, comme le montre explicitement le premier membre.
Et l'on constate que l'égalité supra n'est autre que la définition de la dérivée dS / dr de la fonction S(r) (81), c-à-d son taux de croissance (en l'occurrence, le taux de croissance de la surface en fonction du rayon).
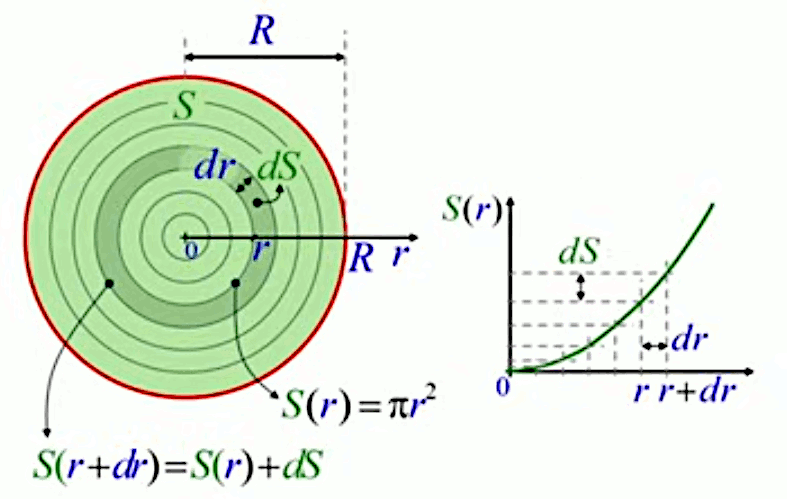
Sur le graphique de droite on voit qu'à un dr correspond un dS, via la fonction S(r).
N.d.A. On peut voir l'axe vertical du graphique de droite ci-dessus comme une "troisième dimension", où l'axe horizontal représente le cercle de droite "couché", et où l'axe vertical mesure l'évolution, par tranches dS, de la surface du cercle au fur et à mesure que l'on s'éloigne de son centre (par l'ajout de dr successifs), c-à-d qu'on se déplace vers la droite sur l'axe horizontal.
Comparons maintenant cette dérivée dS / dr à la notation introduite par Leibniz (point 3 supra) :
dS = 2 * π * r * dr ⇒
de sorte que :
dS / dr = 2 * π * r ⇒
Où l'on constate qu'en effet, comme nous l'avons appris à calculer (cf. supra #derivee) :
dS(R) / dr = S'(R)= (π * R2)' = 2 * π * R
Et si maintenant on substitue cette valeur dans :
S(R) = ∫ dS = ∫0R 2 * π * r * dr (103) ⇒
S(R) = ∫ dS = ∫0R dS / dr * dr
Ce dernier membre peut paraître redondant (puisque 1/dr*dr=1), mais il est pourtant la clé de la résolution de ce problème de sommation d'un nombre infini de grandeurs infiniment petites : une fonction est l'intégrale de sa dérivée :
F(X) = ∫0X F'(x) * dx.
Autrement dit, l'intégrale est l'opération inverse de la dérivée. L'égalité ci-dessus montre bien que ces deux opérations se neutralisent. C'est cela qui permet de calculer une intégrale, vue comme la fonction qui dérivée donne l'intégrande (en l'occurrence F'(X)=2*π*R, qui est la la fonction que l'on intègre (que l'on somme), ou encore la dérivée de l'intégrale.
Exprimons maintenant la dynamique de :
S(R) = ∫ dS = ∫0R 2 * π * r * dr (103)
comme suit :
S(R+dr) = ∫0R+dR 2 * π * r * dr ⇔
S(R+dr) = ∫0R 2 * π * r * dr + 2 * π * R * dR ⇔
c-à-d la surface du cercle de rayon R, plus celle de son anneau d'extension (différentiel) de surface dS :
S(R+dR) = S(R) + 2 * π * R * dR ⇔
S(R+dR) - S(R) = 2 * π * R * dR ⇔
dS = 2 * π * R * dR ⇔
dS / dR = 2 * π * R
soit le même résultat que supra, mais qui montre que la dérivée de l'intégrale c'est l'intégrande, ce que l'on peut noter mathématiquement comme suit :
d∫0X f(x) * dx / dX = f(X)
N.d.A. Attention à bien distinguer x minuscule (la variable d'intégration) et X majuscule (la borne supérieure).

Voilà qui donne la clé de résolution du calcul intégral : calculer une intégrale ∫0X f(x) * dx consiste à trouver la fonction qui, dérivée, donne l'intégrande f(X)
Ainsi, en comparant les trois égalités suivantes :
S(R) = ∫0R 2 * π * r * dr (103)
S(r) = π * r2
dS / dr = 2 * π * r
on a bien que l'intégrale de :
2 * π * r
c'est la fonction :
S(r) = π * r2
dont la dérivée donne l'intégrande :
dS / dr = 2 * π * r
Et donc :
S(R) = ∫0R 2 * π * r * dr = π * R2
Primitive. Il reste un petit problème à régler :
S(r) = π * r2
et
S(r) = π * r2 + C
ont la même dérivée ... (puisque la dérivée d'une constante vaut zéro). Or, en l'occurrence, la surface du cercle c'est π * r2 et non pas π * r2 + C.
Pour résoudre cette problématique, on introduit la notion de primitive P(r) d'une fonction S(r), qui est cette fonction augmentée d'une constante quelconque C :
P(r) = S(r) + C ⇒
P(0) = S(0) + C ⇒
P(0) = 0 + C ⇔
C = P(0) ⇒ substitué dans la première égalité ci-dessus :
S(r) = P(r) - P(0)
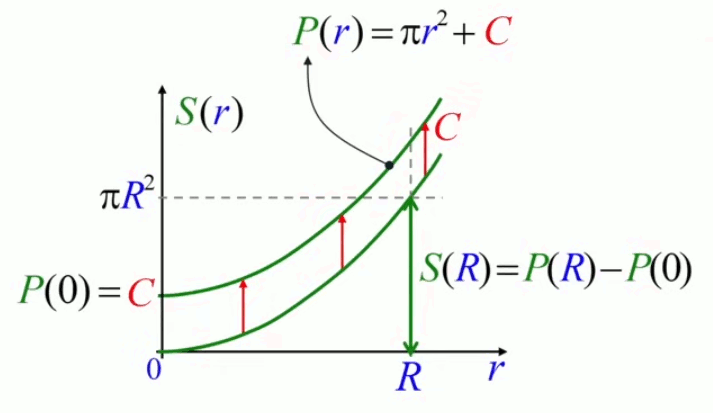
Ainsi en calculant l'intégrale par rapport à la primitive de l'intégrande, on résout le problème de la constante d'intégration. Cela conduit à la notation en crochets, qui caractérise la résolution d'une intégrale :
S(R) = ∫0R 2 * π * r * dr = [ P(r) ]0R = P(R) - P(0)
ainsi en l'occurrence :
P(R) - P(0) = π * R2 + C - ( π * 02 + C ) ⇔
P(R) - P(0) = π * R2 + C - 0 - C
où l'on voit que C se neutralise systématiquement.
Le cas ci-dessus est trivial car la borne inférieure y est nulle. Mais l'intérêt de la notion de primitive apparaît plus clairement lorsque la borne inférieure est non nulle. Calculons ainsi la surface de l'anneau qui va du rayon a au rayon R, c-à-d de a en R sur l'axe des abcisses du graphe de S(r).
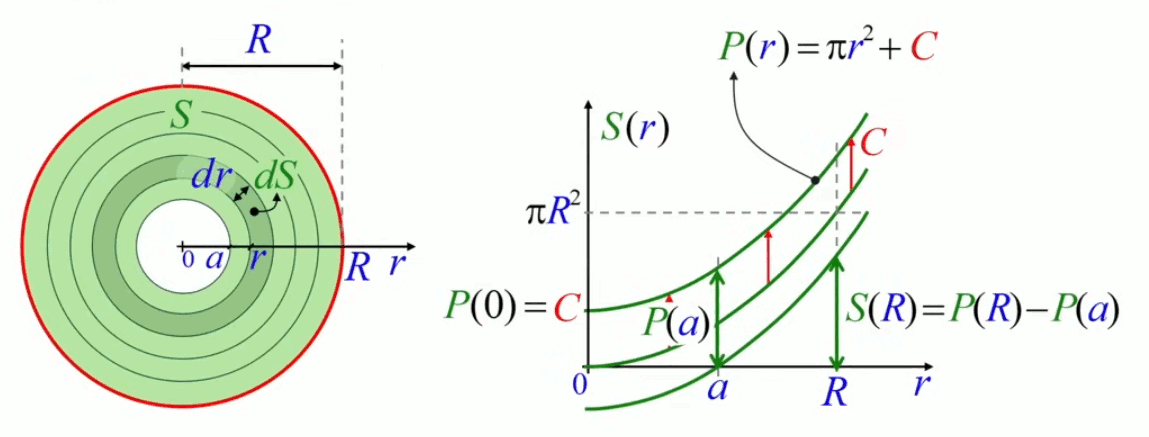
Cette fois, la borne inférieure de l'intégrale n'est plus zéro mais a :
S(R) = ∫0R 2 * π * r * dr = [ P(r) ]aR = P(R) - P(a) ⇔
où l'on voit que la soustraction P(R) - P(a) revient, sur le graphe de S(r), à abaisser la courbe P(r) jusqu'à ce qu'elle coupe l'axe des abscisses en a. La logique apparaît dans la comparaison avec la situation équivalente dans le schéma de gauche : la sommation de la décomposition infinitésimale commence bien en a, moment où la surface que l'on commence à mesurer est encore égale à zéro :
S(R) = ∫0R 2 * π * r * dr = [ P(r) ]aR = P(R) - P(a) = π * R2 + C - ( π * a2 + C ) = π * R2 - π * a2
... qui est un résultat intuitif : la surface de l'anneau est bien la différence entre celles des deux cercles qui le déterminent.
Pratique du calcul intégral
Nous allons déterminer la formule exprimant le volume de la sphère en fonction de son rayon, d'abord avec la méthode géométrique d'Archimède, puis au moyen de la formalisation proposée par Leibniz deux mille ans plus tard, sous forme de calcul intégral.
Dans les deux cas, ont été choisis, comme éléments ΔSn de la décomposition infinitésimale de la surface S = ∑n=1N→∞ΔSn de la sphère, les anneaux (ou bandes annulaires) que séparent deux parallèles (définies en analogie au système de parallèles et méridiens qui permet de se repérer à la surface de la Terre).
À l'instar des triangles utilisés pour la décomposition infinitésimale du cercle, ces anneaux sont de formes identiques, ce qui facilite la sommation de leurs surfaces, lesquelles sont en outre plus faciles à calculer que les formes de fuseaux/lentilles déterminées par les méridiens. D'autre part, ce sont également des anneaux (mais dans un plan) que l'on avait utilisés supra dans le développement de la formule de la surface du cercle par le calcul intégral. Nous allons voir que l'on peut reprendre le même calcul de leur surface.
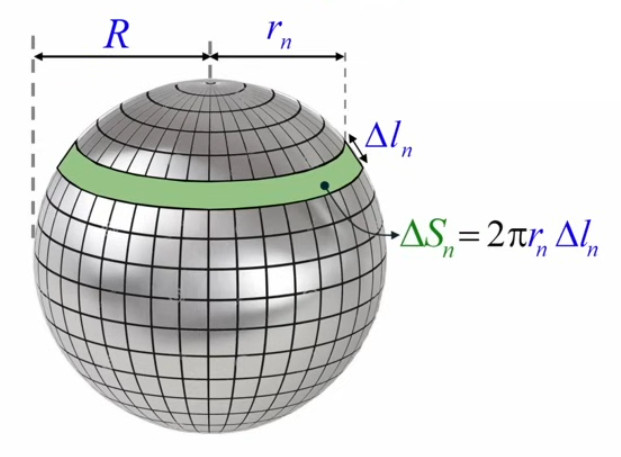
Ces bandes rectangulaires sont d'autant plus inclinées par rapport à l'axe de la sphère qu'elles sont situées près d'un des deux pôles, et d'autant plus proches de la "verticale" (c-à-d parallèles à l'axe de la sphère), qu'elles sont fines et proches de l'équateur.
À l'équateur, on se retrouve alors dans une situation équivalente à celle de l'élément de décomposition infinitésimale du cercle de surface :
S = ∑n=1N→∞ΔSn = ∑n=1N→∞ 2 * π * rn-1 * Δr
(101)
c-à-d que la surface de cette bande particulière de la sphère se calcule simplement par :
base * hauteur
c-à-d en l'occurrence :
périmètre * largeur
soit :
ΔSequ = 2 * π * R * Δl où R est le rayon de la sphère et Δl la hauteur de la bande.
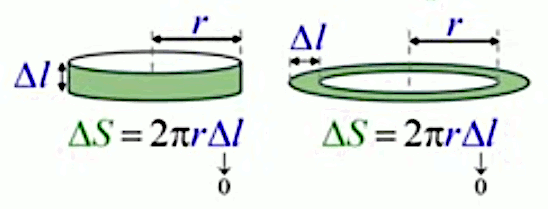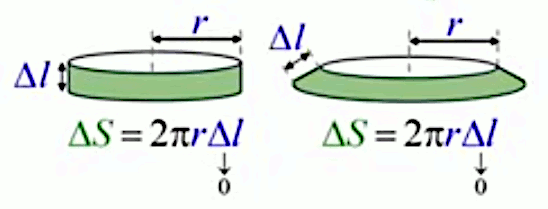
N.d.A. La position verticale correspond à l'équateur, où r=R, tandis que la position horizontale correspond à la situation limite opposée, située aux pôles, où r=0. Au fur et à mesure que l'on se déplace vers un pôle, la surface de la bande diminue avec r. Quant à Δl, il tend vers zéro, pas seulement avec le nombre N de bandes, mais aussi en raison de la conception de cet élément infinitésimal choisi pour la surface de la sphère, comme montré infra.
N.d.A. L'animation ci-dessus illustre un continuum entre les deux situations :
bande aplatie du cercle (2D) ⇒ bande verticale de la sphère (3D)
de sorte que, dans l'égalité supra, on peut remplacer R par rn, et ΔSequ par ΔSn :
ΔSn = 2 * π * rn * Δln
N.d.A. C'est ce que on appelle "faire des math avec les mains". En l'occurrence, il me semble que ce sont de très grosses mains de maçon ;-) . Mais il s'agit ici de vulgarisation, ce qui exige parfois de prendre certaines libertés avec la rigueur mathématique ("passages en force"), pour faire court, ou encore lorsque le public cible ne dispose pas des connaissances requises pour la démonstration.
Dans cette approche "avec les mains", on n'a défini Δln que très sommairement, comme étant la distance (c-à-d la droite la plus courte) entre deux parallèles. Comme nous voulons formuler la surface de la sphère en fonction de son rayon R, nous allons devoir faire de même avec Δln. Pour ce faire, nous allons utiliser l'axe Z de la sphère (la droite passant par ses pôles) comme référentiel par rapport auquel la hauteur des parallèles va être repérée.
N.d.A. Pourquoi la lettre Z ? Ce choix exprime le fait illustré dans le schéma précédent, qui montre le passage de l'anneau aplati (2D ⇔ axes X et Y) à l'anneau vertical (3D ⇔ X, Y, Z).
Le schéma suivant montre que l'axe Z est décomposé en tranche d'épaisseurs identiques Δz = zn - zn+1.
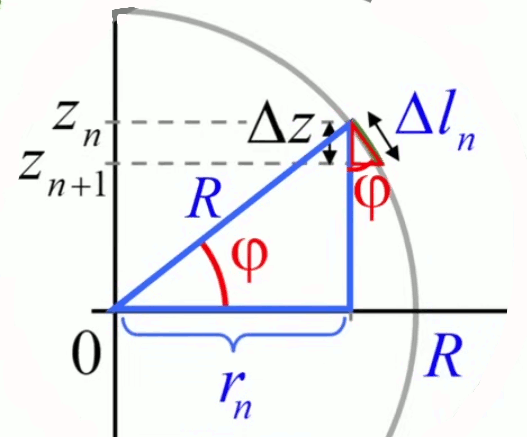
- un rayon rn : qui diminue de l'équateur (rn=R) aux pôles (rn=0) ;
- un Δln : qui diminue de l'équateur (Δln=Δz) aux pôles (Δln=0).
Le lien entre Δln et Δz est déterminé par l'angle φ auquel correspond deux triangles semblales (cf. /geometrie#triangles-semblabes), dessinés en bleu et rouge.
Les deux angles φ sont bien égaux puisque (i) le rayon R est perpendiculaire à Δln, et (ii) la somme des angles d'un triangle vaut 180° (30). Par conséquent, l'angle φ de droite vaut bien 90° - (90° - φ) = φ.
Visionnez bien sur l'illustration que Δln est l'hypoténuse du petit triangle (N.B. ne confondez sa base avec le trait courbé qui dessine l'angle φ, dessiné aussi en rouge).
On peut alors utiliser la propriété des triangles semblables, à savoir que les rapports des côtés homologues sont égaux, et en l'occurrence que le rapport des hypoténuses Δln / R vaut celui des côtés adjacents homologues Δz / rn :
Δln / R = Δz / rn ⇔
rn * Δln = R * Δz ⇔
que l'on substitue dans :
ΔSn = 2 * π * rn * Δln
(104) ⇒
ΔSn = 2 * π * R * Δz
que l'on substitue dans :
S(R) = ∑n=1N→∞ΔSn ⇒
S(R) = ∑n=1N→∞2 * π * R * Δz ⇔
S(R) = 2 * π * R * ∑n=1N→∞Δz ⇔
S(R) = 2 * π * R * 2 * R ⇔
S = 4 * π * R2
CQFD
Cette démarche fut celle d'Archimède (3° siècle av. J.-C.), puis, deux mille ans plus tard, du formalisme mathématique proposé par Leibniz, ... que nous allons maintenant appliquer au même calcul de la surface de la sphère.
Version
Leibniz
La variable d'intégration est donc z, qui va permettre de décrire mathématiquement la décomposition infinitésimale. Deux points de l'axe Z séparés par une distance infinitésimale dz déterminent deux parallèles déterminant la surface infinitésimale dS, élément de cette décomposition infinitésimale de la surface S(R) de la sphère.
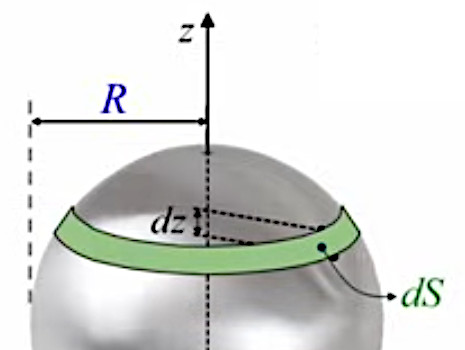
Le changement par rapport à la méthode d'Archimède est que la notation :
ΔSn = 2 * π * rn * Δln
(101)
devient, dans la notation de Leibniz :
dS = 2 * π * r * dl
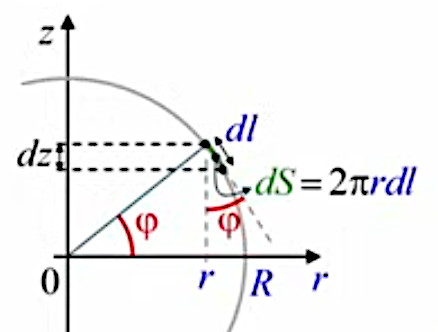
Pour exprimer dl en fonction de z, Archimède avait utilisé la propriété des triangles semblables. Deux mille ans plus tard, à l'époque de Leibniz, la notion de cosinus permet de formaliser, via la variable d'intégration z, la démarche correspondante des triangles semblables :
cos φ = dz / dl (32) ⇔
dl = dz / cos φ
que l'on substitue dans :
dS = 2 * π * r * dl ⇒
dS = 2 * π * r * dz / cos φ ⇒
Il reste à exprimer r et cos φ en fonction de z :
r = R * cos φ (32) ⇔
r / cos φ = R
que l'on substitue dans la formulation de dS supra ⇒
dS = 2 * π * R * dz
Nous allons maintenant sommer ces dS :
S(R)= ∫ dS ⇔
S(R)= ∫-RR 2 * π * R * dz ⇔
S(R)= 2 * π * R * ∫-RR dz ⇔
S(R)= 2 * π * R * ∫-RR 1 * dz ⇔
S(R)= 2 * π * R * [z]-RR ⇔
S(R)= 2 * π * R * [ R - (-R) ] ⇔
S(R)= 2 * π * R * 2 * R ⇔
S(R)= 4 * π * R2
CQFD
Pour calculer le volume de la sphère en fonction de son rayon, l'intuition nous conduit naturellement à nous inspirer de la méthode utilisée pour le calcul intégral de la surface du cercle (cf. vidéo "Décomposition infinitesimale et integration" ). Les éléments de la décomposition infinitésimale du cercle étaient les anneaux qui le composent, identifiables par leur rayon r (la variable d'intégration) et leur épaisseur dr (arbitrairement petite), de sorte que leur surface dS = 2 * π * r * dr (102), où l'on notera que 2 * π * R est le périmètre du cercle (26), et l'intégrante de l'intégrale de la surface du cercle S(R) = ∫ dS = ∫0R 2 * π * r * dr (103). Ainsi la surface du cercle est donc calculée sur base de sa circonférence (N.d.A. : on peut exprimer cela de façon plus typologique en disant que le "contenu" est calculé à partir du "contenant").
Dans la même logique, on va chercher le "contenu" de la sphère c-à-d son volume V(R), à partir de son "contenant" c-à-d sa surface S(R)= 4 * π * R2 (106). Pour ce faire, on va décomposer le volume de la sphère en ... coquilles sphériques, qui jouent dans l'espace 3D de la sphère, le rôle que jouaient les anneaux dans l'espace 2D du cercle.
Le schéma ci-dessous représente une coupe transversale de la sphère. On y montre une coquille de rayon r (la variable d'intégration), d'épaisseur dr (grandeur arbitrairement proche de zéro) et de volume dV (élément de la décomposition infinitésimale).

N.d.A. Dans cette coupe transversale, dV est le volume compris entre deux sphères, l'une contenant l'autre, leurs surfaces respectives étant séparées d'une distance dr (épaisseur de la coquille).
C'est en sommant les volumes des coquilles de cette décomposition que l'on va obtenir le volume de la sphère. Dans le cas de la décomposition infinitésimale de la surface du cercle, celle de ses anneaux se calculait comme la surface d'un rectangle de longueur 2 * π * r (périmètre interne de l'anneau) et de hauteur dr (épaisseur de l'anneau).
Intuition. Dans la même logique, l'intuition nous conduit à calculer le volume d'une coquille en multipliant sa surface interne S(R) = 4 * π * r2 (106) par son épaisseur dr :
dV = 4 * π * r2 * dr ⇒
V(R) = ∫ dV ⇒
V(R) = ∫ 4 * π * r2 * dr ⇔
V(R) = 4 * π * ∫0R r2 * dr ⇔
V(R) = 4 * π * [ 1/3 * r3 ]0R ⇔
V(R) = 4/3 * π * R3
CQFD
N.B. Dans les deux cas (surface du cercle et volume de la sphère), le calcul de la surface/volume déplié est une approximation de la surface/volume originel. L'erreur d'approximation peut-être considérée comme négligeable dès lors que le différentiel (dr) de la variable d'intégration (r) est une grandeur arbitrairement petite.
La formule (107) est le résultat auquel était arrivé Archimède ... à une époque où le calcul intégral était encore inconnu !
L'intuition que dV = 4 * π * r2 * dr était donc bien pertinente. On peut le vérifier sans recourir à la démonstration d'Archimède. Pour ce faire, il suffit de calculer cette différentielle :
dV = V(r+dr) - V(r) ⇒ par (107) :
dV = 4/3 * π * (r + dr)3 - 4/3 * π * r3 ⇔
dV = 4/3 * π * [ (r + dr)3 - r3 ] ⇔
dV = 4/3 * π * [ r3 + 3 * r2 * dr + 3 * r * (dr)2 + (dr)3 - r3 ] ⇔
N.d.A. Le lecteur est invité à vérifier que :
( a + b ) * ( a + b ) = a2 + 2 * a * b + b2
⇒ ( a + b )3 = a3 + 3 * a2 * b + 3 * a * b2 + b3
dV = 4/3 * π * [ 3 * r2 * dr + 3 * r * (dr)2 + (dr)3 ] ⇔
dV = 4/3 * π * [ 3 * r2 + 3 * r * dr + dr2 ] * dr ⇒
dr étant infiniment petit, les deux derniers termes du facteur entre [ ] peuvent être ignorés ⇒
dV = 4/3 * π * [ 3 * r2 ] * dr ⇔
dV = 4 * π * r2 * dr
CQFV
N.d.A. Les termes supprimés 3 * r * dr + dr2 expriment la différence de surface entre sphères dépliée et originelle. Cette différence peut être considérée comme négligeable dès lors que dr est une grandeur infinitésimale c-à-d arbitrairement petite. C'est là que réside la puissance du calcul intégral.
Faisons un bilan comparatif :
-
Cercle :
dS = 2 * π * r * dr ⇔
dS / dr = 2 * π * r = C ⇔
la surface du cercle, dérivée relativement à son rayon, donne sa circonférence ⇔
la circonférence donne le taux de croissance de la surface lorsque le rayon augmente. -
Sphère :
dV = 4 * π * r2 * dr ⇔
dV / dr = 4 * π * r2 = S ⇔
le volume de la sphère, dérivé relativement à son rayon, donne sa surface ⇔
la surface donne le taux de croissance du volume lorsque le rayon augmente.
N.d.A. Dans les deux cas, la dérivée du "contenu" donne le "contenant" ⇔ le "contenant" donne le taux de croissance du "contenu" lorsque la variable d'intégration (ici le rayon r) augmente.
Comme application du calcul intégral démontrons mathématiquement l'équation du MRUA xt = x0 + v0 * t + a * t2 / 2 (164) en appliquant (98) pour calculer la distance parcourue xt - x0 :
xt - x0 = ∫ 0 t v(t') * dt' = V(t)- V(0)
puisque géométriquement cette distance parcourue est la surface en-dessous de la droite vt = v0 + a * t (163) ⇒
V(t) = C + v0 * t + a/2 * t2 ⇒
xt - x0 = C + v0 * t + a/2 * t2 - C ⇔
xt = x0 + v0 * t + a/2 * t2
CQFD
Autre application du calcul intégral : calculer la puissance de l'énergie nucléaire. Celle-ci consiste en la fission du noyau d'atome, ce qui provoque son explosion par expulsion des protons qu'il contient, puisque ceux-ci sont des charges électriques positives, qui se repoussent mutuellement.
La force électrique de répulsion entre les charges positives que sont les protons fournit donc un travail W à ceux-ci, qui acquièrent ainsi une certaine vitesse et, partant, une certaine énergie cinétique Ec = M * v2 / 2 (185). Et en vertu du principe de conservation on a que W = Ec. Or W = f * x(t) (173), mais dans cette formule la force f est considérée comme constante, or la force électrique diminue avec la distance entre les charges : f(r) = kC * q1 * q1 / r 2 (202) (NB : le modèle de calcul est ici composé de deux protons dont l'un est considéré immobile). La solution consiste à considérer la force électrique comme constante sur un segment infinitésimal dx.
Et puisque dx est une grandeur infinitésimale alors c'est aussi le cas du travail correspondant : dW = f(x) * dx (le rectangle bleu dans le graphique ci-dessus) ⇒
W = ∫ dW = ∫ f(x) * dx = [ F(x) ]x0∞ =
[ - kC * qe2 / x ] x0 ∞ =
- kC * qe2 * [ 1 / ∞ - 1 / x0 ] =
- kC * qe2 * 1 / x0
où :
• x0 est la distance entre nucléon du noyau c-à-d la taille d'un nucléon, soit un ordre de 10 * 10-15 m ;
• kC = 9 * 109 N * m2 / C2
• qe = 1,6 * 10 -19 C
⇒ W = 23 * 10 -14 J
ce qui est extrêmement petit ... mais ne concerne qu'un seul proton ⇒ si on considère un nombre de protons égal au nombre d'Avogadro, c-à-d le nombre de protons contenus dans une mole, donc dans un gramme de protons, on obtient alors une valeur nettement plus grande :
1 g : W = 6 * 1023 * 23 * 10 -14 J = 138 * 109 J.
Un gramme de protons contient donc un potentiel d'énergie de milliards de joules !
La fission du noyau d'un atome lourd tel que l'uranium 235 dégage deux millions de fois plus d'énergie que brûler la même masse de charbon...
 Vidéos Clipedia :
Intégration par changement de variable : l'aire du cercle // Calcul intégral : une petite mise au point
Vidéos Clipedia :
Intégration par changement de variable : l'aire du cercle // Calcul intégral : une petite mise au point
Technique
d'intégration
Établir la formule qui donne l'aire du cercle en fonction de son rayon est un cas montrant qu'il est parfois difficile de calculer la primitive de façon usuelle (pratique et mémorisation). Dans ce cas la technique de changement de variable consiste à passer des coordonnées cartésiennes aux coordonnées polaires et d'ainsi obtenir une expression trigonométrique de l'intégrande, dont la primitive est facilement identifiée à partir de la formule du cosinus de l'arc double.
Le premier réflexe est de définir l'intégrande à partir du théorème de Pythagore :
R2 = x2 + y2 (23) (60) ⇔
y = √ ( R2 - x2 ) ⇒
S/4 = ∫ ds = ∫0R y(x) * dx = ∫0R √ ( R2 - x2 ) * dx
Or trouver la primitive de √ ( R2 - x2 ) est très difficile ...
Il est intuitivement facile de comprendre qu'une solution plus adaptée au cercle est d'exprimer ses points en fonction de leur angle correspondant (coordonnées polaires) plutôt que de leur coordonnées x et y :
y = R * cos(θ)
x = R * sin(θ) ⇒
dx / dθ = R * dsin(θ) / dθ ⇒
par (87)
dx / dθ = R * cos(θ) ⇔
dx = R * cos(θ) * dθ ⇒
on substitue les nouvelles expressions de y(x) et dx dans :
S/4 = ∫ ds = ∫0R y(x) * dx ⇒
S/4 = ∫0π/2 R * cos(θ) * R * cos(θ) * dθ ⇔
S/4 = ∫0π/2 R2 * cos2(θ) * dθ

La nouvelle intégrande a une forme différente, mais la surface qui lui correspond est bien égale à S/4.
Maintenant il nous faut trouver la primitive de l'intégrande R2 * cos2(θ) que l'on va simplifier par :
cos(2*θ) = 2 * cos2(θ) - 1 (40) ⇔
cos2(θ) = 1/2 + cos(2*θ) / 2 ⇒
S/4 = R2 * ∫0π/2 [ 1/2 + cos(2*θ) / 2 ] * dθ ⇒
par (88) :
F(θ) = θ / 2 + 1/4 * sin(2*θ) ⇒
S/4 = R2 * [ θ / 2 + 1/4 * sin(2*θ) ]0π/2 ⇔
S/4 = R2 * π/4 ⇔
S = π * R2
Notons que cette démonstration a été développée pour illustrer la technique du changement de variable. Cependant la surface du cercle peut être calculée plus simplement en décomposant le cercle en une somme de triangles de base infinitésimale R * dθ par (1), et dont la surface (notée dS) est donc :
dS = R * dθ * R / 2 = R2 * dθ / 2 ⇒
S = ∫ dS = ∫02π R2 * dθ / 2 ⇔
S = R2 / 2 * [ θ ]02π ⇔
S = π * R2
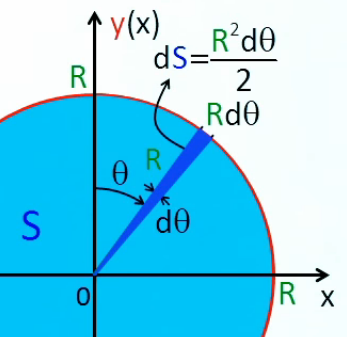
Terminons en notant que ∫ab k = ∞ puisque l'outil intégral est conçu pour sommer des éléments infinitésimaux à l'infini ⇒ si l'élément infinitésimal est absent alors la somme vaut nécessairement l'infini !
Nombre imaginaire et complexe
Les nombres imaginaires facilitent le traitement mathématique de nombreux phénomènes en physique : optique, relativité, mécanique quantique, électricité, ...
1. Nombres imaginaires2. Définition et opérations
3. Représentation géométrique
4. Forme polaire
5. Puissance et racines
Nombres imaginaires
Une règle fondamentale de l'arithmétique en général et des nombre complexes en particulier est que « moins par moins donne plus » : -a * -b = a * b
Mais cette règle pose problème lorsqu'on l'applique à la racine d'un nombre.
Par définition la racine n-ième d'un nombre a – notée √n a – est telle que
( √n a ) n = +/- a si n est paire
et
( √n a ) n = a si n est impaire
ou encore
( √2n a ) 2n = +/- a et ( √2n-1 a ) 2n-1 = a
Il découle de (110) et ( a m ) n = a m*n (8) que √n a = a 1/n
Il y a bien un problème dans le cas où a est négatif et n est paire : par exemple si n=2 alors il résulte de (110) que √-4 * √-4 = +/- 4 ; or il résulte de (109) que le membre de gauche ne peut être que positif ...
La solution au problème décrit ci-avant été inventée au 16° siècle par le physicien et mathématicien Cardano (inventeur du cardan) afin de rendre possible le calcul des racines du polynôme du troisième ordre (a * x3 + b * x2 + c * x + d = 0).
Cette solution consiste à poser que :
√-a = √( -1 * a) = √-1 * √a = i * √a
où par définition i = √-1, appelée "unité imaginaire", est telle que i 2n = -1
Par conséquent, soit a un nombre réel, alors a * i est dit "nombre imaginaire" : I ≡ i * ℝ.
La comparaison des deux droites illustre la nature "d'unité imaginaire" de i autour de zéro, ce dernier étant l'unique valeur commune aux deux ensembles iℝ et ℝ.
Ainsi la solution de l'équation du second degré (78) :
x = ( - b +/- √D ) / ( 2 * a )
D ≥ 0
peut être généralisée en :
x = ( - b +/- d * √|D| ) / ( 2 * a )
d = 1 si D ≥ 0
d = i si D < 0
Ainsi en particulier l’équation x2 = −a où a > 0 a pour solutions x = +/- i * √a
Définition et opérations
Nombres
complexes
Un nombre complexe est la somme d'un terme réel et d'un terme imaginaire : z = x + i * y où x et y sont des réels : ℂ = ℝ +iℝ.
Les opérations sur nombres complexes consistent à appliquer les règles valables pour les réels aux parties des nombres complexes (en prenant en compte le fait que i 2 = −1) : soit z = x + i * y alors les parties réelle et imaginaire sont respectivement x et y (NB : y est appelé "partie" imaginaire tandis que i * y est appelé terme imaginaire ) :
- addition :
( x1 + i * y1 ) + ( x2 + i * y2 ) =
( x1 + x 2 ) + i * ( y1 + y2 ) - multiplication par un réel :
a * ( x + i * y ) =
a * x + i * a * y - multiplication par un autre complexe : distributivité de la multiplication sur l’addition ⇒
( x1 + i * y1 ) * ( x2 + i * y2 ) =
( x1 * x2 − y1 * y2 ) + i * ( x1 * y2 + x2 * y1 )
dont découlent les cas particuliers :- carré :
( x + i * y ) 2 = x 2 - y 2 + i * 2 * x * y
aussi par application du produit remarquable ( a + b ) 2 = a 2 + b 2 + 2 * a * b - multiplication par conjugué (soit z = x + i * y ⇒ z− = x - i * y) :
( x + i * y ) * ( x - i * y ) = x 2 + y 2
aussi par application du produit remarquable ( a + b ) * (a - b ) = a 2 - b 2
N.B. :
• z * z− ∈ ℝ
• on appelle module de z la racine carrée du produit par le conjugué : | z | = √ ( z * z− ) = √ ( x 2 + y 2 ) ⇔
N.d.A. On pourrait dire aussi que la racine carrée du produit d'un nombre complexe par son conjugué correspond à la formule du module d'un vecteur (cf. supra #vecteur-definition) ;
z * z− = x 2 + y 2 ⇔
z * z− = | z |2
d'où découle l'inverse d'un nombre complexe :
1 / z = z− / | z |2
- carré :
- division :
z1 / z2 = z1 * z−2 / | z2 | 2 ⇔
( a + i * b ) / ( c + i * d ) =
( a + i * b ) * ( c - i * d ) / ( c 2 + d 2 )
x + i * y = ( a + i * b ) / ( c + i * d ) ⇔
( x + i * y ) * ( c + i * d ) = a + i * b ⇔
x * c + i * y * c + x * i * d - y * d = a + i * b ⇔
( x * c - y * d ) + i ( y * c + x * d ) = a + i * b
⇔
x * c - y * d = a
x * d + y * c = b
Nous verrons dans la section consacrée aux matrices qu'une façon de résoudre ce système d'équation en (x,y) consiste à le formuler en produit de matrice :
| c | -d |
| d | c |
| x |
| y |
| a |
| b |
dont on sait que la solution est donnée par :
| x |
| y |
| c | d |
| -d | c |
| a |
| b |
⇔
x = (a * c + b * d ) / ( c2 + d2 )
y = ( - a * d + b * c ) / ( c2 + d2 )
⇔
( a + i * b ) / ( c + i * d ) = (a * c + b * d ) / ( c2 + d2 ) + i * ( - a * d + b * c ) / ( c2 + d2 )
Or cette solution on peut donc la trouver plus beaucoup rapidement par (114) :
( a + i * b ) / ( c + i * d ) =
( a + i * b ) * ( c - i * d ) / ( c 2 + d 2 ) ⇔
( a + i * b ) / ( c + i * d ) =
[ a * c - i * a * d + i * b * c + b * d ) * ( c - i * d ) ] / ( c 2 + d 2 ) ⇔
( a + i * b ) / ( c + i * d ) =
[ a * c + b * d + i * ( b * c - a * d ) ] / ( c 2 + d 2 ) ⇔
Représentation géométrique
Nous avions souligné supra que la racine carrée du produit d'un nombre complexe par son conjugué correspond à la formule du module d'un vecteur. Voici une autre similitude entre nombre complexe et vecteur : la correspondance entre addition de deux nombres complexes et addition de deux vecteurs :
- z1 + z2 =
( x1 + i * y1 ) + ( x2 + i * y2 ) =
( x1 + x 2 ) + i * ( y1 + y2 ) - v→1 + v→ 2 =
(x1, x2y) + (y1, y2) =
( x1 + x2 , y1 + y2 ) (52)
Cela montre que l'on peut considérer un nombre complexe comme un vecteur, et donc le représenter géométriquement de la même manière : l'axe X pour la partie réelle du nombre complexe, et l'axe Y pour sa partie imaginaire .
Également similarité pour la représentation géométrique et le calcul algébrique du module.
Ainsi les nombres complexes ayant le même module se trouvent sur un cercle de rayon module et centré sur l'origine. On peut également représenter les nombres complexes opposés (symétrique centrale, par rapport à l'origine), conjugués (symétrie axiale, par rapport à l'axe X), ou encore multipliés.
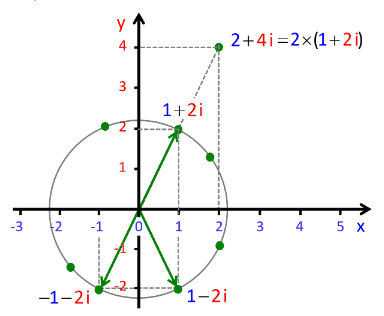
Forme polaire
Nous venons de voir qu'un nombre complexe peut être représenté géométriquement par des coordonnées cartésiennes d'un point. Il peut l'être également par des coordonnées polaires définissant le vecteur position de ce point par deux grandeurs : le module ρ et l'angle θ (appelé "argument" et mesuré relativement à l'axe X) : z = ρ * cos(θ) + i * ρ * sin(θ)
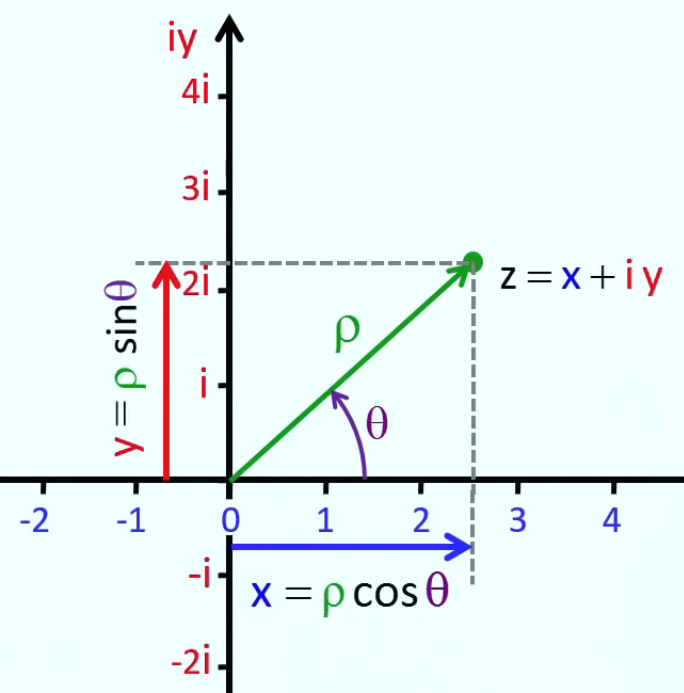
ρ est mesuré positivement dans le sens trigonométrique c-à-d anti-horlogique
Pourquoi "polaire" ? On parle de forme "polaire" par référence au système de méridiens et parallèles utilisé pour déterminer une position sur la surface d'un globe (donc en trois dimensions). Chaque méridien passe par les deux pôles et est défini par un certain nombre de degrés de longitude relativement au méridien de Greenwich. Chaque parallèle coupe les méridiens perpendiculairement et est défini par un certain nombre de degrés de latitude relativement à l'équateur. Si l'on considère le pôle nord comme l'origine (0, 0) du graphique ci-dessus, θ correspond alors à la longitude, et l'axe X au méridien de Greenwich.
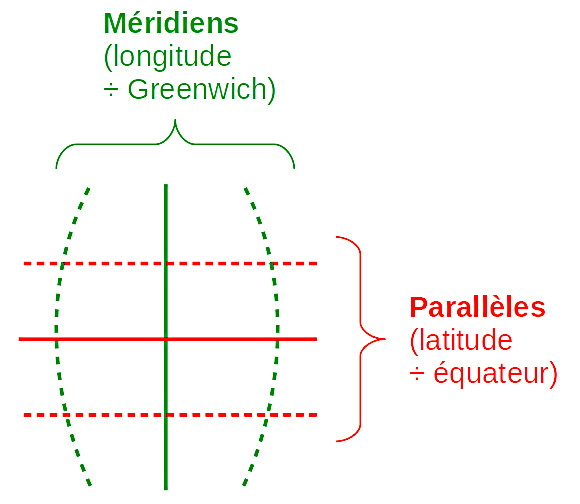
Il y a identité entre le module du nombre complexe et celui du vecteur associé : | z | = ρ
Démonstration :
| z | = √ ( x 2 + y 2 ) (113) ⇔
par (31) et (32) :
| z | = √ ( [ ρ * cos(θ) ] 2 + [ ρ * sin(θ) ] 2 ) ⇔
| z | = ρ * √ ( [ cos(θ) ] 2 + [ sin(θ) ] 2 ) ⇔
par (37)
| z | = ρ
CQFD
Nous avons donc deux formes des nombres complexes :
| forme cartésienne | z = x + i * y |
| forme polaire | z = ρ * cos(θ) + i * ρ * sin(θ) |
Exprimer les coordonnées d'une forme en fonction des coordonnées de l'autre forme est trivial, sauf pour θ :
| Coordonnées cartésiennes | Coordonnées polaires |
| x = ρ * cos(θ) y = ρ * sin(θ) | ρ = √ ( x 2 + y 2 ) θ = arctg( y / x ) |
On démontre géométriquement la valeur de θ en dessinant un cercle centré sur l'origine et de rayon x.
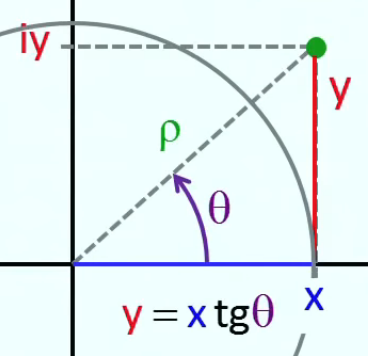
On peut démontrer algébriquement la valeur de θ en divisant membre à membre les deux égalités de la colonne de gauche ci-dessus ⇒
y / x = sin(θ) / cos(θ) ⇔
par (46)
y / x = tg(θ) ⇔
θ = arctg( y / x )
N.B. Lors de l’emploi de la fonction arctan il faut veiller à choisir le quadrant correct pour θ, en ajoutant éventuellement 180° selon les signes des x et y. Ainsi le graphique ci-contre montre que lorsque x<0 la valeur donnée par la calculatrice (ici 56,3°) devra être augmentée de 180° afin d'obtenir la valeur de l'argument du nombre complexe. Cela est du au fait qu'une valeur de tangente correspond toujours à deux valeurs d'angles différant de 180°.
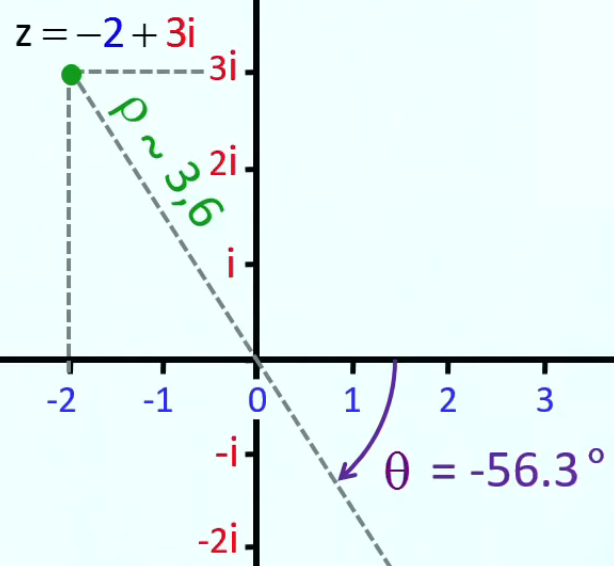
Puissance et racines
 Vidéos Clipedia :
Produits et puissances de nombres complexes // Puissances négatives de nombres complexes
Vidéos Clipedia :
Produits et puissances de nombres complexes // Puissances négatives de nombres complexes
Puissance de
complexe
La forme polaire présente l'avantage de faciliter le calcul des produits et puissances de nombres complexes. La version du produit de complexes sous forme polaire s'obtient de la même façon que sous forme cartésienne (112) : par distribution :
[ ρ1 * ( cosθ1 + i * sinθ1 ) ] * [ ρ2 * ( cosθ2 + i * sinθ2 ) ] =
ρ1 * ρ2 * [ cos(θ1 * cos(θ2) - sin(θ1 * sin(θ2) ] + i * [ cos(θ1) * sin(θ2) + sin(θ1) * cos(θ2) ] =
par (41) et (42) :
ρ1 * ρ2 * [ cos( θ1 + θ2 ) + i * sin( θ1 + θ2 ) ]
⇒ en posant :
ρ1 * ρ2 = ρ3
et
θ1 + θ2 = θ3
puis en réitérant le procédé on voit que l'on peut finalement généraliser par :
∏i=1 n ( ρi * ( cosθi + i * sinθi ) =
∏i=1 n( ρi ) * [ cos(∑i=1 nθi) + sin(∑i=1 nθi) ]
où n est un nombre entier positif, et dont un cas particulier remarquable est celui de ρi = ρ et θi = θ ∀ i :
[ ρ * ( cos(θ) + i * sin(θ) ] n =
ρ n * ( cos( n * θ ) + i * sin( n * θ )
Le graphique ci-contre illustre (117) pour n=2.

Il résulte de (117) que le produit de nombres complexes de module égal à 1 est également un module de valeur 1, de sorte qu'ils sont situés sur le même cercle de rayon 1 et centré sur l'origine. Ainsi le point de ce cercle correspondant à l'angle de 45° a comme partie réelle cos(45) et comme partie imaginaire sin(45) par (115), qui valent toutes deux 1/√2 par (45).
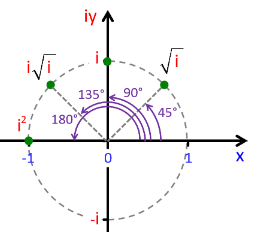
En développant le carré de ce complexe 1/√2 + i * 1/√2 on montre qu'il est égal à √i. Le graphique illustre notamment le cas où il est élevé à la puissance trois : sa valeur devient i * √i et son argument 3*45°=135° par (117).
On va maintenant démontrer que (118) est également vérifiée lorsque n est négatif :
[ ρ * ( cos(θ) + i * sin(θ) ] -n =
ρ -n * 1 / [ ( cos(θ) + i * sin(θ) ] n =
par (117) où ρ=1 :
ρ -n * 1 / [ ( cos( n * θ ) + i * sin( n * θ ) ] =
par (114) :
ρ -n * [ cos( n * θ ) - i * sin( n * θ ) ] / | cos( n * θ ) + i * sin( n * θ ) | 2 =
par (116) où ρ=1 :
ρ -n * [ ( cos( n * θ ) - i * sin( n * θ ) ] =
ρ -n * [ ( cos( - n * θ ) + i * sin( - n * θ ) ]
CQFD
Le graphique ci-dessous illustre géométriquement la forme polaire de la puissance négative d'un nombre complexe, le signe négatif de la puissance ayant pour effet de réduire le module, ce qui est intuitivement cohérent.
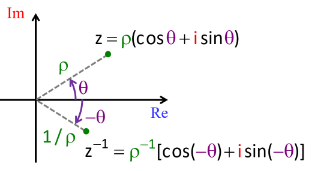
Inverse et quotient de complexe. Il découle de (118) que :
1/z =
1/ρ * ( cos( - θ ) + i * sin( - θ )
⇒
z1 / z2 = z1 * ( 1 / z2 ) =
ρ1 / ρ2 * [ cos( θ1 - θ2 ) + i * sin( θ1 - θ2 ) ]
Racines de
complexe
Nous avons vu que (118) est vérifiée pour n'importe quel nombre n entier. Mais est-ce encore le cas si n est fractionnaire c-à-d si n ∈ ℝ ? La réponse est négative : (118) doit être complétée pour vérifier ce cas.
Pour être mathématiquement rigoureux, il faut préciser que m/n est un nombre rationnel (m et n sont des entiers) or les réels comprennent également les nombres irrationnels (qui ne peuvent s'écrire sous la forme d'une fraction).
En raison de la périodicité des fonctions cosinus et sinus, l'argument d'un complexe est toujours défini à un multiple (k) de 360° c-à-d de 2*π rad près. Il en va donc de même pour le complexe lui-même :
ρ * [ cos(θ) + i * sin(θ) ] =
ρ * [ cos( θ + k * 2 * π ) + i * sin( θ + k * 2 * π )]
où k est un entier (k ∈ ℤ).
Cela est sans effet sur (118) tant que n est entier, mais plus si on le remplace par 1/n car alors on obtient un nombre non entier (k/n) de tours 2*π. Il faut donc le mentionner dans (118) pour obtenir la totalité des racines :
[ ρ * ( cos(θ) + i * sin(θ) ] 1/n =
ρ 1/n * ( cos( θ / n + k / n * 2 * π ) + i * sin( θ + k / n * 2 * π )
où k { 0, 1, 2, ..., n-1 }
Un nombre complexe possède donc n racines n-ièmes distinctes qui correspondent à n valeurs successives de k, comprises entre 0 et n−1. Ces racines sont situées sur le même cercle de rayon ρ1/n et centré sur l'origine. On a bien que 2*π/n est l'écart angulaire entre les arguments des racines, de sorte que la somme des angles ouverts par chaque racine forme 2π.
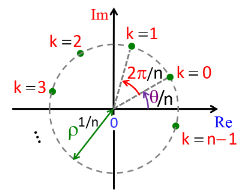
En voici trois exemples.

Analyse combinatoire
Dénombrement
Exemple 1. Dans un pays dont les numéros de plaques minéralogiques sont de type "3 lettres + 3 chiffres", pour déterminer le nombre total de plaques de ce type il faut multiplier entre eux le nombre de cas possibles : 26 * 26 * 26 * 10 * 10 * 10 = 17.576.000.
Le théorème fondamental du dénombrement, ou "principe de multiplication" se formule donc simplement par :
# combinaisons = ∏1pni où
- p est le nombre de positions constituant une combinaison (ici : les six caractères de la plaque minéralogique) ;
- ni est le nombre de valeurs que peut prendre chaque position de la combinaison (ici : le nombre de caractères possibles pour chacun des six caractères de la plaque minéralogique).
N.B. : si ni = n ⇒ # combinaisons = n p. Retenir que "chacune des p positions peut avoir n valeurs".
La valeur de (120) :
varie selon que les ni sont indépendant ou pas : dans l'exemple ci-dessus (plaques minéralogiques) les ni sont indépendants, mais si on impose que les lettres de la plaque minéralogique doivent être différentes (pas de répétitions) alors il n'y a plus indépendance puisque le choix de la première lettre diminuera le nombre de possibilités pour la seconde et la troisième, et que le choix de la seconde diminuera à nouveau le nombre de cas possibles pour la troisième ⇒ le nombre de combinaisons possibles devient : 26 * 25 * 24 * 10 * 10 * 10 = 15.600.000.
correspond à des combinaisons ordonnées : la formule (120) prend en compte l'ordre d'arrangement des ni d'une combinaison, c-à-d compte comme deux combinaisons différentes AB et BA.
Exemple 2. Le tableau ci-dessous montre qu'en recensant (par inversions et distributions) le nombre de combinaisons de quatre lettres (sans répétition d'une même lettre), on obtient un total de 12 ; ce nombre correspond bien à ce que l'on trouve par (120) :
# positions (choisir une lettre puis une seconde) : p=2 ;
ni = { n1=4 ; n2=3 } ;
⇒ ∏1pni = 4 * 3 = 12
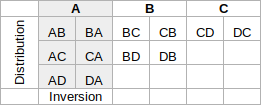
Dans ce dernier cas si on relâche la contrainte de non répétition, on ajoute alors quatre ni (AA,BB,CC,DD) ⇒ 12+4=16, ce qui correspond bien à :
ni = { n1=4 ; n2=4 } ;
⇒ ∏1pni = 4 * 4 = 16
Exemple 3. Si parmi dix compétiteurs on tire au sort les médailles d'or, d'argent et de bronze, combien de combinaisons de compétiteurs médaillés (compositions de podium) peut-on obtenir :
# positions : p=3 ;
ni = { n1=10 ; n2=9 : n3=8} ;
⇒ ∏1pni = 10 * 9 * 8 = 720
 Vidéos Clipedia :
Analyse combinatoire : arrangements // Analyse combinatoire : permutations et factorielles
Vidéos Clipedia :
Analyse combinatoire : arrangements // Analyse combinatoire : permutations et factorielles
Arrangement
L'exemple ci-dessous est un cas particulier de dénombrement, appelé "arrangement", et dont le principe est « parmi n je prends p, et l'ordre compte » (le podium Pierre/Paul/Jean est différent de Paul/Pierre/Jean) . On le note An1p ou plus simplement Anp (A103 dans l'exemple ci-dessus), et on le lit « A n p ».
On peut généraliser sa formulation comme suit :
Anp = n * (n - 1 ) * ( n - 2 ) * ... * ( n - p + 1 ) ⇔
où les premiers facteurs montrent bien que le nombre de résultats par position vaut bien n moins le numéro de la position plus 1
Anp = n * (n - 1 ) * ( n - 2 ) * ... * ( n - p + 1 ) * [ ( n - p ) * ( n - p - 1) * ... * 1 ] / [ ( n - p ) * ( n - p - 1) * ... * 1 ] ⇔
Anp = n ! / ( n - p ) !
Ainsi dans l'exemple précédent on doit attribuer trois médailles parmi dix compétiteurs :
"parmi 10 je prends 3" ⇒
A310 =
10 ! / ( 10 - 3 ) ! =
10 ! / 7 ! =
8 * 9 * 10 = 720
NB : 0!=1 par définition/convention.
Suites mathématiques
Nous allons étudier ici les suite arithmétiques et géométriques.
 Vidéos Clipedia :
Les suites arithmétiques : introduction // Les suites arithmétiques : sommes et applications
Vidéos Clipedia :
Les suites arithmétiques : introduction // Les suites arithmétiques : sommes et applications
Suites
arithmétiques
Une suite (u0, ... un) est dite "arithmétique" si ui = ui-1 + r ∀ i
où r est une valeur constante appelée "raison" de la suite.
Ce principe d'indiçage vaut également pour les suites géométriques.
Graphe. Graphiquement une suite arithmétique se traduit par une droite, et c'est pourquoi l'on parle indifféremment de progression arithmétique ou linéaire [tableur].
Valeur d'un terme quelconque
Un première propriété de la suite arithmétique est que l'on peut calculer la valeur de n'importe lequel de ses termes (un) à partir de son indice (n), de la valeur du premier terme (u0) et de la raison (r) :
un = u0 + n * r
Démonstration à partir de (126) :
un = un-1 + r ⇔
un = (un-2 + r ) + r = un-2 + 2 * r ⇒
que l'on peut généraliser en remplaçant 2 par n :
un = un-n + n * r ⇔
un = u0 + n * r ⇔
CQFD
Valeur de la somme des termes
Par (123) :
∑i=0n ui = ∑i=0n ( u0 + i * r ) ⇔
∑i=0n ui = ( n + 1 ) * u0 + r * ∑i=0n i
Or l'on démontre que :
∑i=0n i = n * ( n + 1 ) / 2
en constatant que si :
• I = (0, 1, 2, 3, ..., n-1, n)
• I' = (n, n-1, ..., 3, 2, 1, 0) ⇒
I + I' = ( U0=n, U1=n, U3=n, ..., Un=n ) ⇔
soit S(I) la somme des termes de la suite I :
2 * S(I) = n * ( n + 1 ) ⇔
S(I) = n * ( n + 1 ) / 2 ⇒
∑i=0n ui = ( n + 1 ) * u0 + r * n * ( n + 1 ) / 2 ⇔
∑i=0n ui = ( n + 1 ) * ( u0 + r * n / 2 )
Ainsi l'on peut calculer la somme d'une suite arithmétique à partir du nombre de ses éléments (n+1), de la valeur du premier élement (u0) et de la raison (r).
N.d.A. On notera que (124) et un cas particulier de (125) où u0=0 et r=1.
On peut également exprimer la somme des termes en fonction de la moyenne :
un = u0 + n * r ⇔
n * r / 2 = ( un - u0 ) / 2 ⇒
∑i=0n ui = ( n + 1 ) * [ u0 + ( un - u0 ) / 2 ] ⇔
∑i=0n ui = ( n + 1 ) * (u0 + un ) / 2 ⇔
∑i=0n ui = ( n + 1 ) * S–n
Suites
géométriques
Une suite (u0, ... un) est dite "géométrique" si ui = ui-1 * r ∀ i
où r est une valeur constante appelée "raison" de la suite.
Graphe. Graphiquement une suite géométrique se traduit par une exponentielle, et c'est pourquoi l'on parle indifféremment de progression géométrique ou exponentielle [tableur].

Valeur d'un terme quelconque
Un première propriété de la suite géométrique est que l'on peut calculer la valeur de n'importe lequel de ses termes (un) à partir de son indice (n), de la valeur du premier terme (u0) et de la raison (r) :
un = u0 * r n
Démonstration à partir de (126) :
un = un-1 * r ⇔
un = (un-2 * r ) * r = un-2 * r 2 ⇒
que l'on peut généraliser en remplaçant 2 par n :
un = un-n * r n
un = u0 * r n
CQFD
Valeur de la somme des termes
Par (127) :
∑i=0n ui = ∑i=0n ( u0 * r i ) ⇔
∑i=0n ui - r * ∑i=0n ui = ∑i=0n ( u0 * r i ) - r * ∑i=0n ( u0 * r i ) ⇔
∑i=0n ui * ( 1 - r ) = ∑i=0n ( u0 * r i ) - ∑i=0n ( u0 * r i+1 ) ⇔
∑i=0n ui * ( 1 - r ) = u0 * ( ∑i=0n r i - ∑i=0n r i+1 ) ⇔
Technique (artifice mathématique) dit de la "somme téléscopique".
∑i=0n ui * ( 1 - r ) = u0 * ( 1 - r n+1 ) ⇔
∑i=0n ui = u0 * ( 1 - r n+1 ) / ( 1 - r )
Ainsi l'on peut calculer la somme d'une suite géométrique à partir du nombre de ses éléments (n+1), de la valeur du premier élement (u0) et de la raison (r).
Raison négative. Si le cas de r<0 est trivial dans le cas d'une suite arithmétique (droite à pente négative) , ce ne l'est plus dans celui d'une suite géométrique car le signe des termes y alterne constamment : c'est alors une oscillation exponentielle que l'on constate (indécelable au début) [tableur].
Problème. Supposons un nénuphar doublant de taille chaque jour, de telle sorte qu'il recouvre la totalité du lac en 365 jours. Après combien de temps a-t-il rempli la moitié du lac ?
Résolution :
Il double de taille chaque jour : r = 2.
Il recouvre la totalité du lac en 365 jours : u365 = 2365 par (127).
⇒ de même, le nombre n de jours après lesquels le lac est à moitié recouvert est tel que :
2365 / 2 = 2 n ⇔
n = log2(2365 / 2) ⇔
n = log2(2365) - log2(2) ⇔
n = 365 - 1 = 364
NB : on peut arriver à ce résultat par un raisonnement plus intuitif : comme la totalité du lac est couverte en i=365 et que la surface double chaque jour, la moitié du lac a donc été couverte en i=365-1 ...
Nous avons vu que les fonctions logarithme et exponentielle sont réciproques (11), de sorte que si l'on applique un affichage logarithmique à une courbe exponentielle on obtient une droite [tableur]. Cela est vrai également dans le cas d'une raison négative, c-à-d d'une sismoïde exponentielle puisqu'il n'y a pas de valeur pour le logarithme d'un nombre négatif (sauf si l'on recourt aux nombres imaginaires).
Résumé
Le tableau suivant permet de comparer les formules des suites mathématiques selon leur type arithmétique ou géométrique.
| Définition | Terme n | ∑ termes | |
|---|---|---|---|
| Arithm. | ui = ui-1 + r | un = u0 + n * r | ∑i=0n ui = ( n + 1 ) * ( u0 + r * n / 2 ) |
| Géom. | ui = ui-1 * r | un = u0 * r n | ∑i=0n ui = u0 * ( 1 - r n+1 ) / ( 1 - r ) |
Démonstration
par récurrence
Pour démontrer (125) nous avions du démontrer que ∑i=0n i = n * ( n + 1 ) / 2, et pour ce faire nous avions eu recours à un développement mathématique basé sur un artifice mathématique (I+I'). Voici une autre démonstration de (125), qui contrairement à la démonstration par développement requiert d'utiliser la proposition dans sa démonstration (donc de la connaître a priori), mais qui présente l'avantage d'être fondée sur une méthode applicable à de nombreuses démonstrations : la démonstration par récurrence.
Cette technique est composée de deux étapes pour démontrer une proposition P(n) ∀ n :
- initialisation : démontrer P(0) ;
- hérédité : démontrer P(n) ⇒ P(n+1) en partant de P(n+1) et en y faisant apparaître P(n) ;
Il faut démontrer également P(n) ⇒ P(n-1) si on ne se limite pas aux nombres naturels et que l'on considère le cas des entiers (ℤ).
- ⇒ P(n) est démontré ∀ n
Alors allons-y : soit Sn = 0 + 1 + 2 + 3 + ... + n ⇒ P(n) ≡ Sn = n * ( n + 1 ) / 2 :
- S0 = 0
et
0 * ( 0 + 1 ) / 2 = 0
⇒ P(0) ≡ S0 = 0 * ( 0 + 1 ) / 2 est démontré. - Sn+1 = 0 + 1 + 2 + ... + n + ( n + 1 ) ⇔ par P(n) :
Sn+1 = Sn + ( n + 1 ) ⇔
Sn+1 = n * ( n + 1 ) / 2 + ( n + 1 ) ⇔
Sn+1 = ( n + 1 ) * ( n / 2 + 1 ) ⇔
Sn+1 = ( n + 1 ) * ( n + 2 ) / 2
⇒ Pn ⇒ Pn+1 est démontré. - ⇒ P(n) ≡ Sn = n * ( n + 1 ) / 2 est démontré ∀ n !
N.B. La démonstration par récurrence peut être utilisée dans d'autres cas que les suites mathématiques. Démontrons ainsi P(n) ≡ d(x n) / dx = n * x n-1 (83) :
- par (6) :
d(x0) / dx = 0
et d'autre part :
0 * x-1 = 0
⇒ P(0) ≡ d(x0) / dx = 0 * x -1 est démontré. - d(xn+1) / dx = d(xn * x ) / dx ⇔ par (85) :
d(xn+1) / dx = d(xn) / dx * x + xn * dx/dx ⇔ par P(n) :
d(xn+1) / dx = n * x n-1 * x + xn ⇔
d(xn+1) / dx = ( n + 1 ) * x n ⇔
⇒ Pn ⇒ Pn+1 est démontré. - ⇒ P(n) ≡ d(x n) / dx = n * x n-1 est démontré ∀ n !
On peut donc distinguer au moins deux types de démonstrations mathématiques :
- par développement : quand on ne connaît pas a priori la proposition à développer (c-à-d qu'on ne peut l'utiliser dans le cadre de la démonstration) ;
- par récurrence : on utilise la proposition P(n) dans sa démonstration, qui consiste à démontrer que P(n) est valable ∀ n.
Fonction exponentielle
2. Exponentielle imaginaire
Exponentielle naturelle
La fonction exponentielle est illustrée ici par le phénomène biologique de division cellulaire de bactéries par fission binaire. La durée d'une fission, appelé temps de génération (TG), se situe en 15 minutes et quelques heures.
Cette fonction est f(x) = 2x où :
• 2 est le nombre moyen d'enfants par génération ;
• x est le nombre de générations par unité de temps.
Pour illustrer la dynamique de la multiplication exponentielle on va mesurer l'espace pris après 24 heures par la multiplication de la bactérie "Escherichia coli", qui constitue 80% de notre flore intestinale (mais dont certaines souches sont pathogènes pour les intestins). Sa taille est environ 2*0,5 µm ("microns") ⇒ sa surface est de 1 µm2 = 10-12 m2 (invisible au microscope optique).
Animation accélérée.
Soit TG=16min ⇒ le nombre de générations après 24 heures est de 24*60/16=90 ⇒ le nombre de bactéries est alors 290=1,24*1027 ⇒ elles occupent une surface de 1,24*1027*10-12 m2=1,24*1015 m2 ... soit plus du double de la surface de la Terre (0,51*1015 m2) ! Ainsi puisque chaque génération double le nombre total de cellules, il en résulte que l'augmentation de surface entre les 89° et 90° générations équivaut à la surface de la Terre ! La croissance exponentielle est donc un phénomène qu'il n'est pas facile d'appréhender intuitivement.
On généralise la formulation de l'exponentielle par f(x) = bx, où :
□ b est la "base" de la fonction exponentielle (cas ci-dessus : nombre moyen d'enfants par génération) ;
□ x = P / Tg est le nombre de fois que la base est reproduite par unité de temps (cas ci-dessus : nombre de générations par jour) :
○ P est la période de référence ;
○ Tg est le temps de génération.
On peut étudier formellement la dynamique de la fonction exponentielle en calculant sa dérivée :
f '(x) = ( f ( x + dx ) - f (x) ) / dx (81) ⇒
(2x)' = ( 2( x + dx ) - 2x ) / dx ⇔ par (5) :
(2x)' = ( 2x * 2dx - 2x ) / dx ⇔
(2x)' = 2x * ( 2dx - 1 ) / dx
où
( 2dx - 1 ) / dx = 0/0 ⇒
pour lever l'indétermination on va tester des petites valeurs de x :
• si dx=0,01 ⇒ ( 2dx - 1 ) / dx = 0,695...
• si dx=0,001 ⇒ ( 2dx - 1 ) / dx = 0,693...
• si dx=0,0001 ⇒ ( 2dx - 1 ) / dx = 0,693... ⇒
(2x)' = 0,693 * 2x
Interprétations :
□ le taux de croissance (la dérivée) de la fonction exponentielle est lui-même une fonction exponentielle (⇒ on comprend mieux maintenant l'impressionnante croissance spatiale de la division cellulaire) ;
□ 0,693 est donc la valeur de la pente de la fonction 2x à l'origine c-à-d pour x=0 :
(2x)'|x=0 = 20 * 0,693 = 0,693.
De même on pourra calculer que :
(10x)' = 2,303 * 2x
Se pose alors une question intéressante : quelle est la valeur de la base b de la fonction bx dont la pente à l'origine vaut 1, c-à-d telle que :
(bx)' = 1 * bx
N.B. Cette fonction est particulière : en tout point, elle est égale à sa dérivée :
(bx)' = bx
Le tableau suivant suggère que la base de cette fonction, que nous allons noter e, se situe entre 2 et 10.
| bx | Pente (bx)' |
|---|---|
| 10x | 2,303 |
| ex | 1 |
| 2x | 0,693 |
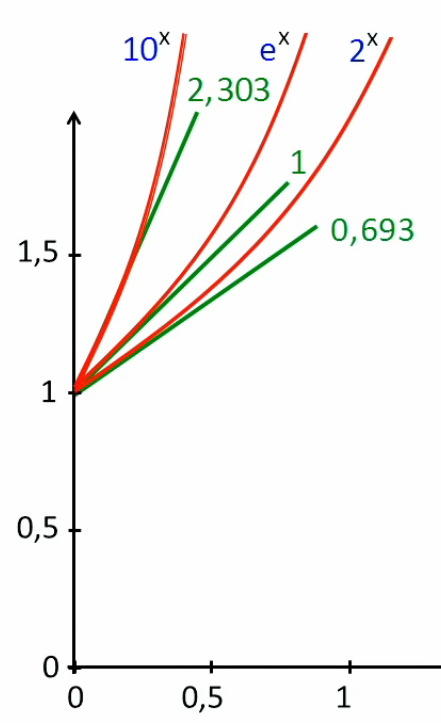
Pour identifier la valeur de e on va à nouveau procéder par essais-erreurs, en partant de b=2 :
• si b=2,5 ⇒ (2,5x)'|x=0 = 0,916 ⇒ je peux encore augmenter la base :
• si b=3 ⇒ (3x)'|x=0 = 1,098 ⇒ je dois diminuer la base :
• si b=2,7 ⇒ (2,7x)'|x=0 = 0,993 ⇒ je dois augmenter la base :
• si b=2,72 ⇒ (2,72x)'|x=0 = 1,001 etc... ⇒
e = 2,718282... (nous verrons plus loin une méthode plus rigoureuse pour calculer e : la méthode d'Euler).
La fonction ex, dite fonction exponentielle naturelle est donc telle que :
(ex)' = ex * ( edx - 1 ) / dx = ex
⇔ la pente à l'origine de la fonction ex étant unitaire, implique qu'en tout point la fonction est égale à sa dérivée (nous verrons plus loin que cette propriété de la fonction exponentielle correspond à la dynamique de nombreux phénomènes physiques).
N.d.A. Cela signifie que la fonction ex croît croît proportionnellement à sa valeur actuelle.
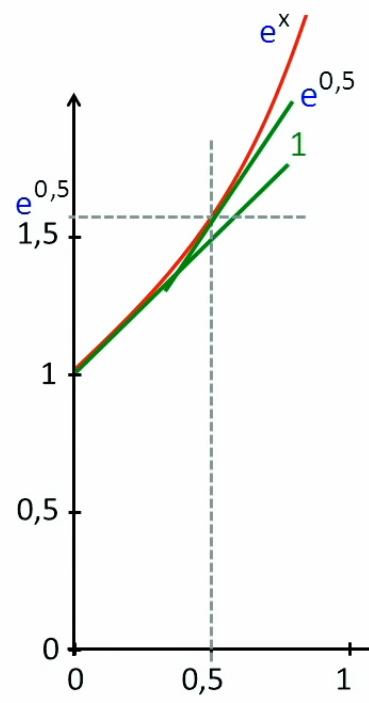
Dénomination et notation :
• la fonction est dite "exponentielle" car la variable x apparaît à l'exposant ;
• la notation ex peut être remplacée par exp(x), ce qui est utile lorsque x est une fonction dont l'écriture comprend de nombreux termes.
La fonction exponentielle est asymptotique (à l'axe horizontal ) pour x --> - ∞ mais il n'y a pas de tendance asymptotique pour x --> + ∞ : x doit augmenter infiniment pour que ex augmente infiniment.
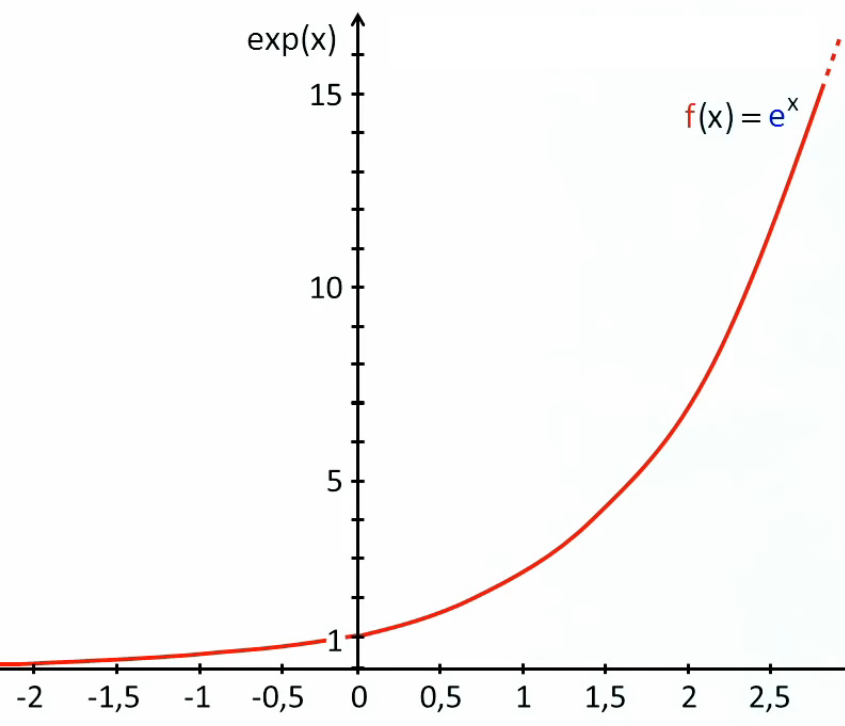
Enfin nous avons vu dans la section consacrée à la fonction logarithme que celle-ci est réciproque de la fonction exponentielle (et réciproquement) :
f(x) = e x ⇔ loge (e x) ≡ ln (e x) = x
(10)
b = e ln(b)
(11)
de sorte que – grâce au logarithme en base e (noté loge), appelé logarithme naturel (noté ln) – on peut exprimer une exponentielle de base quelconque comme une exponentielle de base e :
bx = ( e ln(b) ) x ⇔ par (8) :
bx = e ln(b) * x ⇒
( bx ) ' = ( e ln(b) * x ) ' ⇔ par (88) :
( bx ) ' = d( e ln(b) * x ) / d( ln(b) * x ) * d(ln(b) * x) / dx ⇔ par (129) :
( bx ) ' = e ln(b) * x * ln(b) ⇒
soit ln(b) = a ⇒
( e a * x ) ' = a * e a * x
qui est une d'équation différentielle de type f '(x) = a * f(x), qui permet de décrire de nombreux phénomènes physiques où biologiques dont la variation est proportionnelle à la grandeur elle-même,et dont la solution est de type exponentielle.
Fonction exponentielle vs polynomiale (N.d.A.)
Ne pas confondre :
fonction exponentielle : a * bx +c, où la variable (x) est en exposant ;
fonction polynomiale : bn * xn + bn-1 * xn-1 + ... b1 * x + c, où la variable est en base (cf. le cas de la parabole, fonction polynomiale de degré 2 : /geometrie#equation-second-degre).
Une fonction exponentielle croît beaucoup plus rapidement qu'une fonction polynomiale (pour x=10, x2=100, mais 2x=1024) et n'a pas de sommets (elle peut tendre vers zéro ou croître indéfiniment). Quant à la fonction polynomiale, elle peut-être symétrique (forme en "∪" ou en "∩", et donc, en l'occurrence, avoir un minimum ou un maximum).
Utilisations :
- exponentielle : modéliser la croissance d'une population, la décroissance radioactive, les intérêts composés, ...
- polynomiale : modéliser des trajectoires, des courbes et des surfaces (dans la conception de structures, d'ailes d'avion, ou de coques de navires), le maximum ou minimum d'une fonction, ...
La méthode appliquée supra pour calculer la valeur de e est grossière. La méthode d'Euler permet de calculer facilement cette valeur, avec une précision arbitraire. Elle repose sur le fait qu'aucune autre fonction que f(x)=ex est telle que f(x)'=f(x). Elle consiste à utiliser une fonction f(x) que l'on fait progressivement approcher de ex :
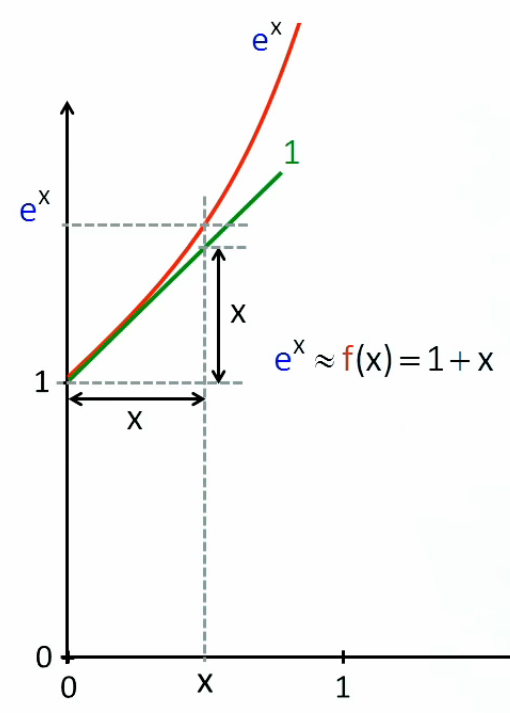
Étape 1. On commence avec l'équation de la tangente de ex à l'origine. :
f(x) = 1 + x
qui est telle que :
limx→0 1 + x = ex
Étape 2. On complète f(x) pour en faire polynôme du second degré :
f(x) = 1 + x + a * x2
⇒ on calcule la valeur de a telle que f(x) vérifie la propriété caractéristique de l'exponentielle c-à-d telle que :
f(x)' = f(x) ⇒
( 1 + x + a * x2 )' = 1 + x + a * x2 ⇔
1 + 2 * a * x = 1 + x + a * x2 ⇔
a = 1 / ( 2 - x )
or :
limx→0 1 / ( 2 - x ) = 1/2
⇒ on pose a=1/2 ⇒ :
f(x) = 1 + x + 1/2 * x2
Étape 3. On complète f(x) pour en faire un polynôme du troisième degré :
1 + x + 1/2 * x2 + b * x3 ⇒
on calcule la valeur de b telle que f'(x) = f(x) :
( 1 + x + 1/2 * x2 + b * x3 )' = 1 + x + 1/2 * x2 + b * x3 ⇔
b = 1 / ( 6 - 2 * x )
or :
limx→0 1 / ( 6 - 2 * x ) = 1/6
⇒ on pose b=1/6 ⇒ :
f(x) = 1 + x + 1/2 * x2 + 1/6 * x3 ⇒
Étape 4. On complète f(x) pour en faire un polynôme du quatrième degré :
1 + x + 1/2 * x2 + 1/6 * x3 + c * x4 ⇒
on calcule la valeur de b telle que f'(x) = f(x) :
( 1 + x + 1/2 * x2 + 1/6 * x3 + c * x4 )' = 1 + x + 1/2 * x2 + 1/6 * x3 + c * x4 ⇔
c = 1 / ( 24 - 6 * x )
or :
limx→0 1 / ( 24 - 6 * x ) = 1/24
⇒ on pose c=1/24 ⇒ :
f(x) = 1 + x + 1/2 * x2 + 1/6 * x3 + 1/24 * x4
où l'on constate que les dénominateurs ui des coefficients constituent une suite de type :
ui = i !
où i est également le degré polynomial associé au terme de la suite; ou encore le rang du terme dans la suite.
Étape 5. On peut alors, par généralisation à un degré arbitraire n, établir la formulation de f(x) pour une précision arbitraire n :
f(x) = 1/0! + 1/1! * x + 1/2! * x2 + 1/3! * x3 + 1/4! * x4 + ... + 1/n! xn ⇒
f(x) = ∑n=0∞ xn / n!
NB : 0!=1 par définition.
On obtient ainsi la décomposition en série entière de la fonction exponentielle :
ex = ∑n=0∞ xn / n!
⇒ pour calculer la valeur de e il suffit de poser x=1 ⇒
e = ∑n=0∞ 1 / n! ⇔
e = 1 +1 + 1/2 + 1/6 + 1/24 + ... = 2,71828182846...
Euler a montré qu'il s'agit d'un nombre irrationnel c-à-d ne pouvant être égal au quotient de deux nombres.
Exponentielle imaginaire
Exponentielle
imaginaire
Il peut être utile dans certains calculs de transformer une exponentielle imaginaire de base quelconque b i en exponentielle naturelle e f(i) :
par (11) :
b i = ( e ln(b) ) i ⇔
par (8) :
b i = e i * lnb
Plus généralement on souhaite exprimer la fonction :
f(θ) = e i * θ (où θ ∊ ℝ)
sous forme de son complexe :
f(θ) = e i * θ = x(θ) + i * y(θ)
⇒ on doit déterminer les fonctions x(θ) et y(θ).
N.B. Alors que i * θ est l'argument de l'exponentielle, θ est l'argument de l'exponentielle imaginaire. D'autre part, θ ∊ ℝ signifie que θ ne peut être un nombre complexe, sinon il s'agirait d'une exponentielle complexe (i * θ où θ est un réel est dit "imaginaire pure").
par (113) :
| e i * θ | 2 = e i * θ * e -i * θ ⇔ par (5) :
| e i * θ | 2 = e 0 ⇔ par (6) :
| e i * θ | 2 = 1
⇔ le graphe de la fonction e i * θ a la forme d'un cercle centré sur l'origine des axes représentant les parties réelle et imaginaire du complexe x(θ) + i * y(θ).
Étape 2. Pour définir l'équation de ce cercle on va commencer par calculer sa dérivée : par (130) :
de i * θ / dθ = i * e i * θ
Étape 3. On exprime f(θ) sous forme polaire :
f(θ) = e i * θ = x(θ) + i * y(θ) ⇔ par (115) :
f(θ) = e i * θ = cos[ φ(θ) ] + i * sin[ φ(θ) ]
⇒ en identifiant φ(θ) on pourra identifier
• x(θ) = cos[ φ(θ) ]
• y(θ) = sin[ φ(θ) ]
- On substitue le résultat de l'étape 3 – la forme complexe polaire de f(θ) – dans celui de l'étape 2 ⇒
de i * θ / dθ = i * e i * θ = i * ( cos[ φ(θ) ] + i * sin[ φ(θ) ] ) ⇒
de i * θ / dθ = i * e i * θ = i * cos[ φ(θ) ] - sin[ φ(θ) ] - D'autre part on égalise le résultat de l'étape 2 à la dérivée de la forme complexe de f(θ) :
i * e i * θ = [ x(θ) + i * y(θ) ] ' ⇔
i * e i * θ = x '(θ) + i * y '(θ) ⇒ par (31) et (32) :
i * e i * θ = ( cos[ φ(θ) ] ) ' + i * ( sin[ φ(θ) ] ) ' ⇔ par (86) (87) (88) :
i * e i * θ = - sin[ φ(θ) ] * φ '(θ) + i * cos[ φ(θ) ] ) * φ '(θ)
- ⇒ on constate l'égalité des résultats des deux points ci-dessus :
i * cos[ φ(θ) ] - sin[ φ(θ) ] = - sin[ φ(θ) ] * φ '(θ) + i * cos[ φ(θ) ] ) * φ '(θ) ⇔
i * cos[ φ(θ) ] - sin[ φ(θ) ] = ( - sin[ φ(θ) ] + i * cos[ φ(θ) ] ) * φ '(θ) ⇔
φ '(θ) = 1 ⇒
φ(θ) = θ + c
or le graphique montre que φ(θ=0)=0 ⇒
φ(0) = 0 + c = 0 ⇔
c = 0 ⇒
φ(θ) = θ
φ(θ) est donc tout simplement la fonction identité.
• x(θ) = cos[ φ(θ) ] = cos(θ)
• y(θ) = sin[ φ(θ) ] = sin(θ)
⇒ la formule d'Euler :
e i * θ = cos(θ) + sin(θ) * i
où θ est en radians.

• e i * 0 = 1
• e i * π/2 = i
• e i * π = -1 ⇔ e i * π + 1 = 0 ("identité d'Euler", qui combine ainsi cinq nombres remarquables : 0, 1, π, e, i)
• e i * 3π/2 = -i
Nous allons maintenant illustrer le fait que l'exponentielle imaginaire e i * θ est la représentation algébrique du cercle trigonométrique.
Commençons par souligner le fait que le cercle trigonométrique a pour caractéristique que son rayon vaut 1 :
par (113) :
| e i*θ | = √ ( cos2(θ) + sin2(θ) ) ⇔
par (37) :
| e i*θ | = 1
ce qui implique que θ doit être un nombre réel c-à-d qu'il ne peut être un nombre complexe :
ei*(a+i*b) = ei*a-b = ei*a * e-b
or
| ei*a | = 1 ⇒
| ei*a * e-b | = | ei*a | * e-b = e-b = 1 ⇔ b=0
CQFD
Poursuivons notre illustration de l'exponentielle imaginaire en posant la question suivante : soit a un nombre réel, quelle est la signification mathématique et géométrique de ai ? (PS : objet abstrait puisqu'il s'agit de multiplier a i fois par lui-même ...).
Nous avons vu que :
a i = ( e ln(a) ) i ⇔
a i = e i * ln(a)
Ainsi a i est le point du cercle trigonométrique correspond à l'angle d'arc-tangente ln(a) (en vert).)
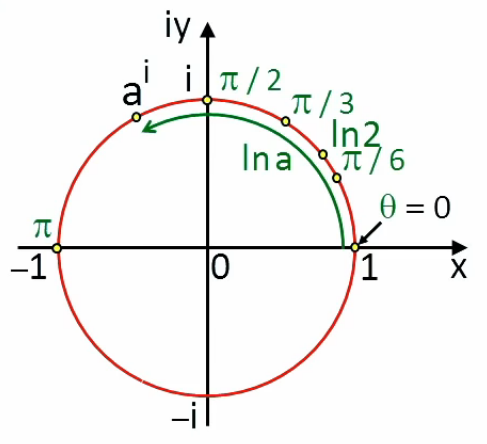
Logarithme imaginaire. Il est alors facile de trouver la valeur de ln(i) :
eln(i) = i
et d'autre part :
e i * π/2 = cos(π/2) + i * sin(π/2) = i ⇒
e i * π/2 = eln(i) ⇔
ln(i) = i * 1/2 * π + i * 2*k*π
De la même manière on trouve la valeur de ln(-i) en identifiant le point du cercle trigonométrique correspondant à -i ⇒ on voit qu'il s'agit de 3π/2 :
eln(-i) = -i
et d'autre part :
e i * 3*π/2 = cos(3*π/2) + i * sin(3*π/2) = -i ⇒
e i * 3π/2 = eln(-i) ⇔
ln(-i) = i * 3/2 * π + i * 2*k*π
De même on trouve la valeur de ln(-1) en identifiant le point du cercle trigonométrique correspondant à -1 ⇒ on voit qu'il s'agit de π :
ln(-1) = i * π + i * 2*k*π
N.B. Ce dernier résultat est remarquable : on peut maintenant calculer le logarithme d'un nombre négatif :
ln(-|x|) = ln(-1 * |x| ) ⇔ par (14) :
ln(-|x|) = ln(-1) + ln(|x|) ⇔
ln(-|x|) = ln(|x|) + i * π + i * 2*k*π
qui est un nombre imaginaire dont la partie réelle vaut ln(|x|) et la partie imaginaire vaut π+2*k*π.
Applications. On va maintenant montrer que l'exponentielle imaginaire est très pratique pour représenter les nombres complexes et en étudier les propriétés.
Ainsi l'on va pouvoir démontrer plus simplement certaines propriétés des nombres complexes, à commencer par la formule du produit de complexes (117) : soit :
z = ρ * ( cos(θ) + i * sin(θ) ) ⇒ par (131) :
z = ρ * e i*θ ⇒
z1 * z2 = ρ1 * ρ2 * e i*θ1 * e i*θ2 ⇔
z1 * z2 = ρ1 * ρ2 * e i*(θ1+θ2)
que l'on peut généraliser à :
∏i=1 n zi = ∏i=1 n( ρi ) * e i * ∑i=1 nθi
où n est un nombre entier positif, et dont un cas particulier remarquable est celui de :
ρi = ρ et θi = θ ∀ i ⇒
z n = ρ n * e i * ( n * θ )
• qui est valable pour n < 0 ⇒
- inverse : 1 / z = 1 / ρ * e i * ( - θ )
- division : z 1 / z 2 = z 1 * 1 / z 2 = ρ 1 / ρ 2 * e i * ( θ1 - θ2 )
• qui est aussi valable pour n fractionnaire ⇒
- z1/n = ρ 1/n * e i * [ 1/n * (θ+2kπ) ]
La notion d'exponentielle imaginaire facilite également la démonstration de propriétés de fonctions trigonométriques, à commencer par la fonction sin(2*a). Pour ce faire on part de la formule d'Euler :
e i * θ = cos(θ) + sin(θ) * i
(131)
qui nous dit que le cos est la partie réelle du complexe, et le sin sa partie imaginaire :
• cos(θ) = Re[ei*θ]
• sin(θ) = Im[ei*θ]
⇒
sin(2a) = Im[ei*2*a] ⇔ par (5) :
sin(2a) = Im[ei*a * ei*a] ⇔
sin(2a) = Im[ ( cos(a) + i * sin(a) ) * ( cos(a) + i * sin(a) ) ] ⇔
sin(2a) = Im[ cos2(a) - sin2(a) + i * 2 * cos(a) * sin(a) ) ] ⇔
sin(2a) = 2 * cos(a) * sin(a) ⇔
CQFD
qui est effectivement plus simple que la démonstration géométrique de (41).
On procède de même pour démontrer :
cos(a+b) = Re[ e i*(a+b) ] ⇔
cos(a+b) = Re[ e i*a * e i*b ] ⇔
cos(a+b) = Re[ ( cos(a) + i * sin(a) ) * ( cos(b) + i * sin(b) ) ] ⇔
cos(a+b) = Re[ cos(a) * cos(b) - sin(a) * sin(b) + i * (...) ] ⇔
cos(a+b) = cos(a) * cos(b) - sin(a) * sin(b) ]
CQFD
Encore une fois on est plus obligé de démontrer géométriquement par des montages sur le cercle trigonométrique, grâce au fait que la fonction exponentielle imaginaire est une représentation mathématique du cercle trigonométrique ⇒ on peut rester dans le domaine de l'algèbre.
Pour terminer on va démontrer :
cos(a) + cos(b) =
2 * cos[ ( a + b ) / 2 ] * cos[ ( a - b ) / 2 ]
en partant du fait que par (111) :
cos(a) + cos(b) = Re[ e i*a + e i*b ] ⇔
en appliquant un artifice mathématique :
cos(a) + cos(b) = Re[ e i*(a+b)/2 * ( e i*(a-b)/2 + e - i*(a-b)/2 ) ]
où :
e i*(a-b)/2 + e - i*(a-b)/2
est la somme de deux complexes conjugués.
Or :
e i*a + e -i*a = [ cos(a) + i * sin(a) ] + [ cos(a) - i * sin(a) ] = 2 * cos(a) ⇔
cos(a) = ( e i*a + e - i*a ) / 2
qui est la définition moderne du cosinus, ou encore que cos(a) est la partie réelle de ei*a !
De la même manière on démontre que :
sin(a) = ( e i*a - e - i*a ) / ( 2 * i )
⇒
e i*(a-b)/2 + e - i*(a-b)/2 = 2 * cos[ (a-b) / 2 ]
NB : qui est un nombre réel ⇒
cos(a) + cos(b) = Re[ e i*(a+b)/2 ] * 2 * cos[ (a-b) / 2 ] ⇔
cos(a) + cos(b) = cos[ (a+b) / 2 ] * 2 * cos[ (a-b) / 2 ]
CQFD
Cette démonstration aurait été nettement plus ardue sans recourir à l'exponentielle imaginaire, ce qui confirme la puissance de celle-ci pour résoudre de nombreux problèmes mathématiques, mais également modéliser de nombreuses applications caractérisées par des variations harmoniques c-à-d sinusoïdales :
- le nuage électronique qui vibre avec une certaine fréquence (ω dans la formule de l'image ci-contre) ;
- l'onde que propage le laser ;
- les variations du courant et de la tension de l'électricité alternative.
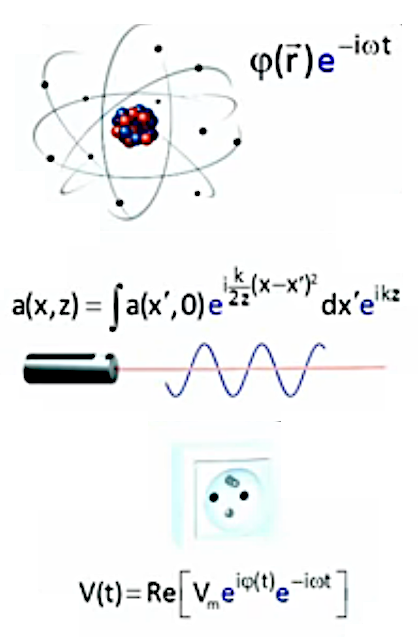
Matrices
2. Déterminant et matrice inverse
3. Addition matricielle
4. Produit matriciel
5. Matrice identité
6. Transformation
7. Plan et volume
8. Formule générale du déterminant et cofacteur
9. Propriétés du déterminant
10. Matrice inverse
11. Déterminant d'un produit de matrices
Définition
Solutions
système
équations
Nous allons voir que l'objet mathématique qu'est la matrice permet de simplifier le calcul des solutions d'un système d'équations, et d'ainsi rendre possible des applications technologiques impliquant un grand nombre de variables et paramètres. Voici la façon la plus fréquente de formuler un système d'équations linéaires à deux inconnues x et y (les autres grandeurs, appelées "paramètres", étant considérées comme connues) :
a * x + b * y = pc * x + d * y = q
dont on constate que les membres de gauche correspondent à des produits scalaires (59) :
(a, b) . (x, y) = p(c, d) . (x, y) = q
de sorte que le système peut être représenté sous forme matricielle comme suit :
| a | b |
| c | d |
| x |
| y |
| p |
| q |
dont la règle de calcul est formulée par (138). Nous verrons une généralisation de cette règle de calcul. Mais pour cela il nous faut d'abord développer les notions de matrice inverse et de déterminant.
Rappel (N.d.A.) : une condition nécessaire pour obtenir la valeur de toutes les inconnues d'un système d'équations est que le nombre d'équations égale le nombre d'inconnues, c-à-d que la matrice rouge ci-dessus soit carrée.
Déterminant et matrice inverse
En simplifiant l'écriture de la forme matricielle ci-dessus par A * X = P, on définit alors le membre de gauche comme étant un "produit matriciel", et dont la règle de calcul est comme suit :
- première ligne de P : produit scalaire de la première ligne de A avec la "matrice colonne" X (on dit aussi "vecteur colonne") ;
- seconde ligne de P : produit scalaire de la deuxième ligne de A avec la colonne de X.
Il résulte de A * X = P que l'on pourrait calculer simultanément l'ensemble des solutions du système par le produit : X = A-1 * P.
Il nous faut donc approfondir la notion de matrice inverse (A-1), ce que l'on va faire grâce au moyen d'un objet mathématique très utile : le déterminant d'une matrice.
Pour ce faire on va commencer par calculer les solutions de (138), sans recourir aux matrices. Pour ce faire on procède comme suit :
- multiplier :
- la première équation par le coefficient de y dans la seconde équation (d) ;
- la seconde équation par le coefficient de y dans la première équation (b) :
( c * x + d * y ) * b = q * b - soustraire les deux équations pour éliminer y :
a * d * x - b * c * x = d * p - b * q ⇔
x = ( d * p - b * q ) / ( a * d - b * c ) - appliquer les étapes 1 à 2 pour obtenir la valeur de y ⇒
x = d * p − b * q / ( a * d − b * c )
y = a * q − c * p / ( a * d − b * c )
Déterminant
de A
On constate que les deux solutions ont même dénominateur : a * d − b * c. On l'appelle "déterminant de A" car si sa valeur est nulle il détermine que x et y sont infinis c-à-d que le système n'a pas de solution. Il est noté det(A) et l'on constate que sa valeur correspond au produit scalaire des éléments de la diagonale principale (↘) de A par ceux de l'autre diagonale (↙) :
| a | b |
| c | d |
N.d.A. La notion de déterminant ne concerne donc que les matrices carrées.
Inverse
de A
Nous verrons plus loin que la résolution de nombreux calculs d'ingénierie requiert l'utilisation de l'inverse d'une matrice. Or la notion de déterminant va nous permettre de formuler simplement l'inverse d'une matrice.
En effet, en entroduisant ce nouvel objet qu'est le déterminant, le système des solutions que nous avons calculées (140) peut alors s'écrire plus simplement :
det(A) * x = d * p − b * q
det(A) * y = a * q − c * p
que l'on ordonne pour symétriser :
det(A) * x = d * p - b * q
det(A) * y = - c * p + a * q
de sorte que les deux membres peuvent être écrits sous forme matricielle :
| det(A) * x |
| det(A) * y |
| d | -b |
| -c | a |
| p |
| q |
On met alors det(A) en évidence puis on le fait passer dans le membre de droite, de sorte que l'on obtient la forme matricielle du système des solutions du système (139) :
| x |
| y |
| d | -b |
| -c | a |
| p |
| q |
que l'on compare à :
X = A-1 * P
pour en déduire que :
A-1 = 1 / det(A) *
| d | -b |
| -c | a |
Où l'on notera que la matrice ressemble quelque peu à A, sauf que :
• les éléments que la diagonale principale (↘) sont intervertis ;
• les éléments que la diagonale secondaire (↙) ont changé de signe.
Par conséquent on peut conclure que l'écriture :
A * X = P ⇒ X = A-1 * P
vaut également pour des matrices (pour autant, nous le verrons plus loin, que le produit matriciel soit possible, ce qui requiert que les matrices soient telles que A pxn * B nxq, c-à-d telles que le nombre de colonnes de A est égal au nombre de lignes de B).
N.d.A. La méthode du déterminant, pour déterminer l'inversibilité d'une matrice et calculer son inverse, ne concerne donc que les matrices carrées.
Addition matricielle
La comparaison des deux formulations d'un système d'équations (138) et (139) suggère que le produit d'une matrice par un scalaire, ainsi que l'addition de matrices, s'opèrent en appliquant élément par élément de matrice les principes du produit et de l'addition de scalaires. On comprend également que ne peuvent être additionnées que des matrices de dimensions #lignes x #colonnes égales.
Notation. Dans les indices de matrices le premier chiffre indique le nombre de lignes, et le second le nombre de colonnes. Ainsi la matrice Amxn est de dimension mxn, c-à-d est composée de m lignes et n colonnes (NB : mxn est donc le nombre d'éléments de la matrice). Dans le cas des opérations d'algèbre matricielle on utilise une notation en fonction des éléments aij :
Amxn =| a11 | a12 | ... | a1n |
| a21 | a22 | ... | a2n |
| ... | ... | ... | ... |
| am1 | am2 | ... | amxn |
où :
i=1,...,m : indique la ligne de l'élément aij;
j=1,...,n : indique la colonne de l'élément aij.
Ainsi l'on démontre facilement la distributivité de la multiplication scalaire sur l’addition de matrices :
α * [ A + B ] =
α * [ (aij) + (bij) ] =
α * ( aij + bij ) =
[ α * ( aij + bij ) ] =
( α * aij + α * bij ) =
( α * aij ) + ( α * bij ) =
α * ( aij ) + α * ( bij ) =
α * A + α * B
CQFD
On démontre de la même manière :
- l'associativité de l’addition de matrices : [A+B]+C=A+[B+C]
- la commutativité de l’addition de matrices : A+B=B+A
Application
Une matrice constitue un outil mathématique idéal pour représenter et modifier une image numérique :
- chaque élément de la matrice correspond à un point de l'image (pixel) ;
- la valeur de chaque élément correspond à l’intensité lumineuse du point correspondant ;
- la dimension de la matrice correspond à celle de l'image.
Ainsi dans le cas simple d’une image monochrome :
- la matrice nulle, c-à-d ne comportant que des zéros, correspond à une image noire ⇔ la somme d’une image quelconque avec une image noire redonne l’image de départ, et pas une image noire ;
- on créé un effet de fondu (superposer deux images) en additionnant les matrices correspondant à ces images ;
- on modifie la luminosité d'une image en multipliant sa matrice par un scalaire.
Produit matriciel
Nous disposons maintenant des éléments nécessaires pour définir le produit matriciel général. On peut le faire facilement à partir du produit de deux matrices carrées, que l'on détermine comme suit :
| a | b |
| c | d |
| e | f |
| g | h |
| x |
| y |
| a | b |
| c | d |
| e * x + f * y |
| g * x + h *y |
| a * ( e * x + f * y ) + b * ( g * x + h *y ) |
| c * ( e * x + f * y ) + d * ( g * x + h *y ) |
| ( a * e + b * g ) * x + ( a * f + b * h ) * y |
| ( c * e + d * g ) * x + ( c * f + d * h ) * y |
cf. passage de (138) à (139)
| a * e + b * g | a * f + b * h |
| c * e + d * g | c * f + d * h |
| x |
| y |
⇒ par comparaison avec la première égalité :
| a | b |
| c | d |
| e | f |
| g | h |
| a * e + b * g | a * f + b * h |
| c * e + d * g | c * f + d * h |
où l'on constate que l'élément i j de la matrice produit C=A*B est égal au produit scalaire de la ligne i de A par la colonne j de B, ce que l'on formule mathématiquement comme suit :
c i j = a i 1 * b 1 j + a i 2 * b 2 j = ∑k=12a i k * b k j
Et l'on voit que cette formule peut être généralisée au produit :
A pxn * B nxq = C pxq
où :
c i j = a i 1 * b 1 j + ... + a i n * b n j =
∑ k=1na i k * b k j.
NB : le nombre de colonnes de A doit être égal au nombre de lignes de B, sans quoi le produit scalaire ne serait pas possible.
Application. Il suffit des quatre lignes de code suivantes pour programmer la transcription informatique du dernier membre de la formule mathématique (144). Cet algorithme permet à un ordinateur de calculer en quelques secondes une matrice produit scalaire comportant des millions d'éléments :
// Pour chaque ligne de la matrice produit Cpxq : for (i=0;i<p;i++) // et pour chaque colonne de la matrice produit C pxq : for (j=0;j<q;j++) // le produit scalaire ligne * colonne s'effectue : for (k=0;k<n;k++) // en cumulant les produits des éléments homologues : c[i][j]+=a[i][k]*b[k][j];
Notez la similitude entre la dernière ligne de l'algorithme et le dernier membre de (144).
Matrice 1x1. On notera qu'une matrice 1x1 n'est pas un scalaire :
(c11) = C1x1 = A1xn * Bnx1 =
| a11 | a12 | ... | ann |
| b11 |
| b21 |
| ... |
| b2n |
(c11 = ∑ k=1na i k * b k j)
qui est donc une matrice ne contenant qu'un seul élément, mais qu'il ne faut pas confondre avec le scalaire c11 ! Ainsi la multiplication d'une matrice quelconque ( dij ) par un scalaire est toujours possible :
c11 * ( dij ) = ( c11 * dij )
mais ce n'est pas le cas du produit de cette matrice quelconque par une matrice C1x1=( c11 ) :
( c11 ) * ( dij )
qui n'est n'est possible que si i=1
À noter également que si l'on commute les matrices du produit :
A1xn * Bnx1 = C1x1
on obtient :
Bnx1 * A1xn = Cnxn
qui est donc une matrice nxn !
| b11 |
| b21 |
| ... |
| b2n |
| a11 | a12 | ... | a1n |
| b11*a11 | ... | b11*a1n |
| ... | ... | ... |
| b2n*a11 | ... | b2n*a1n |
Propriétés du produit matriciel :
- Non commutativité :
Soit
A lxn * B nxm = C lxm
alors
B nxm * A lxn
n'est possible que si m=l c-à-d si A et B sont de dimensions inverses, ou égales si elles sont carrées (NB : cette condition de commutativité est nécessaire, mais pas suffisante !) ⇒ le produit matriciel n'est donc pas commutatif en toute généralité. CQFD.N.B. Le produit d'une matrice par son inverse est commutatif :
A-1 * A = I ⇔
A * A-1 * A = A * I = A ⇔
A * A-1 = I
CQFD - Distributivité de la multiplication matricielle sur l’addition matricielle :
A * ( B + C ) =
(aik) * [ (bkj) + (ckj) ] =
(aik) * ( bkj + ckj ) =
par (144) :
( ∑ k=1na i k * ( bkj + ckj ) ) =
par distributivité entre scalaires, puis regroupements b et c :
( ∑ k=1na i k * bkj + ∑ k=1na i k * ckj ) =
( ∑ k=1na i k * bkj ) + ( ∑ k=1na i k * ckj ) =
A * B + A * C
CQFD - Associativité :
(A * B ) * C =
[ (ail) * (blk) ] * (ckj) =
( ∑l a il * b lk ) * (ckj) =
( ∑k [ ∑l a il * b lk ] * ckj ) =
( ∑k [ ∑l a il * b lk * ckj ] ) =
par commutativité de la somme :
( ∑l [ ∑k a il * b lk * ckj ] ) =
mise en évidence de a il :
( ∑l [ a il * [ ∑k b lk * ckj ] ] ) =
( a il ) * ( ∑k b lk * ckj ) =
( a il ) * [ ( b lk ) * ( ckj ) ] =
A * ( B * C )
CQFD
Matrice identité
| a | b |
| c | d |
On calcule sa valeur comme suit :
A-1 * A =par (143) :
1 / det(A) *
| d | -b |
| -c | a |
| a | b |
| c | d |
1 / det(A) *
| a * d - b * c | 0 |
| 0 | a * d - b * c |
⇒ par (141) :
I =
| 1 | 0 |
| 0 | 1 |
Quant à la définition de la matrice identité, on peut la généraliser au cas d'une matrice carrée quelconque nxn :
I = (ipq) où ipq =
0 si p≠q
1 si p=q
et que l'on démontre comme suit :
A * I = (aik) * (ikj) ⇔
par (144)
A * I = ( ∑k=1na i k * i k j ) ⇔
par définition (146) :
A * I = ( a i1 * i 1j + a i2 * i 2j +... + a ij * i jj + ... + a in * i nj )
où tous les i sont nuls sauf i jj=1 ⇒
A * I = (aij) = A
CQFD (même principe pour I*A).
On démontre enfin qu'une matrice identité est nécessairement carrée, à partir de l'égalité :
I lxn * A nxm = A lxm
qui n'est possible pour A que si n=l
CQFD
Nous sommes maintenant en mesure de démontrer une quatrième propriété du produit matriciel :
[A * B]−1 = B−1 * A−1
que l'on démontre en commençant par montrer que :
A * B * B−1 * A−1 = A * A−1 = I
⇒ si on multiplie par [A * B]−1 les deux membres extrêmes de cette chaîne d'égalités ⇒
[A * B]−1 * A * B * B−1 * A−1 = [A * B]−1 ⇒
B−1 * A−1 = [A * B]−1
CQFD
Transformation
Le calcul matriciel permet notamment d'opérer des transformations géométriques simples, qui sont des applications linéaires bijectives (symétrie, agrandissement, rétrécissement, rotation, cisaillement, perspective, etc). Nous allons étudier ici la transformation d'une image par transformation de ses coordonnées : X'2x1 = A2x2 * X2x1 où les vecteurs colonnes X et X' sont les vecteurs positions d'un pixel dans chacune des images, et A2x2 est la matrice de transformation.
Ainsi la symétrie axiale d'axe y d'une image (cf. graphique infra) peut s'écrire :
x' = -xy' = y
⇔
| x' |
| y' |
| -1 | 0 |
| 0 | 1 |
| x |
| y |
Symétrie axiale d'axe Y
De même que n’importe quelle matrice carrée 2×2 peut être considérée comme une transformation d’image (ou encore comme une transformation du plan), plus généralement, une matrice carrée 3×3 peut être considérée comme une transformation d’objet à trois dimensions (transformation de volume).
Nous allons maintenant étudier quelques propriétés remarquables de transformations matricielles.
Réversion
La première propriété est particulièrement intuitive : l'inverse d'une matrice transformation est la matrice de la transformation inverse (on dit aussi "réciproque") :X’ = A * X ⇔
A−1 * X’ = A−1 * A * X ⇔
A−1 * X’ = X
CQFD
NB : il résulte de de la formule de la matrice inverse (143) qu'une transformation dont le déterminant est nul est par conséquent non réversible (dans le cas des transformations d'image, on dit que l'information sur l'image originelle a été perdue lors de la transformation).
Matrice égale à son inverse :
à l'instar des scalaires :
A = A−1 ⇔ A2 = I
mais contrairement aux scalaires il n'y pas seulement A=I et A=-I comme solutions : il existe une infinité de matrices ayant pour propriété d'être égale à leur inverse. C'est par exemple le cas de la matrice telle que :
| -1 | α |
| 0 | 1 |
| -1 | α |
| 0 | 1 |
| 1 | 0 |
| 0 | 1 |
Transformations
multiples
La matrice B * A est la matrice d’une seule transformation équivalente à la transformation B appliquée à la transformation A :
X" = B * X' = B * A * X
À noter que l'ordre des transformations est l'inverse de celui de leur écriture formelle du produit, ce qu'il importe de ne pas perdre de vue dès lors qu'un produit matriciel n'est pas nécessairement commutatif (il l'est cependant dans certains cas, comme par exemple si la transformation par A est une symétrie axiale d'axe Y, et la transformation par B une symétrie axiale d'axe X).
Vecteurs
unitaires
transformés
Pour analyser plus en profondeur le principe de transformation, on va identifier la transformation des
points de coordonnées (1, 0) et (0, 1), qui sont les coordonnées des vecteurs de base unitaires :
1x→ =
| 1 |
| 0 |
| 0 |
| 1 |
Les vecteurs transformés sont :
| a | b |
| c | d |
| 1 |
| 0 |
| a |
| c |
et
| a | b |
| c | d |
| 0 |
| 1 |
| b |
| d |
Où l'on voit que les colonnes successives de la matrice transformation carrée représentent des vecteurs qui sont les transformées de chacun des vecteurs de base .
Ainsi l'on comprend, plus intuitivement, que par exemple la matrice :
| α | 0 |
| 0 | 1 |
... a pour effet de modifier la largeur de l'image, puisque l'unité de l'axe X (colonne de gauche) est multipliée par α tandis que l'unité de l'axe Y (colonne de droite) est inchangée.
Rotation
Dans le cas d'une rotation d'un angle θ les figures suivantes illustrent le vecteur 1x→ et sa transformation (deux figures de gauche : représentation vectorielle et sa transformée en représentation cartésienne), puis le vecteur 1y→ et sa transformation (deux figures de droite : représentation vectorielle et sa transformée en représentation cartésienne) :

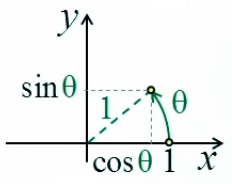
| a |
| c |
| cos θ |
| sin θ |
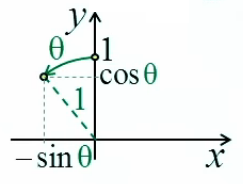
| b |
| d |
| - sin θ |
| - cos θ |
de sorte que :
| a | b |
| c | d |
| cos θ | - sin θ |
| sin θ | cos θ |
D'où il résulte que le déterminant d'une rotation vaut 1 :
det(A) = a * d - b * c = (cosθ)2 + (sinθ)2 ⇔
par (37) :
det(A) = 1
CQFD
Plan et volume
Nous allons voir que :
- une matrice 2x2 (/ 3x3) correspond à la transformation d'une surface (/ d'un volume) ;
- cette propriété est liée au fait que le produit vectoriel (/ mixte) correspond à une surface (/ un volume).
- la valeur du déterminant de cette matrice donne le facteur de dilatation de la surface (/ du volume) par la transformation ;
- cette propriété est liée au fait que le produit vectoriel (/ mixte) vaut le ("se calcul au moyen du") déterminant de la matrice dont les colonnes (ou les lignes) sont les vecteurs du produit.
Le lecteur attentif aura remarqué que l'interprétation d'une matrice comme expression d'une transformation correspond à un changement de notation dans le système d'équations (138) où les constante p et q ont été remplacées par la coordonnée (x', y') du point transformé ⇒
a * x + b * y = x'
c * x + d* y = y'
2D
On constate qu'un segment de droite avant transformation reste un segment de droite après une telle transformation, mais en général d’orientation et de longueur différentes. En particulier le segment déterminé par les points (0,0) et (1,1), c-à-d le vecteur position (1,1), est transformé en vecteur position (a+b,c+d). Ainsi le carré unitaire est transformé en parallélogramme.
| a | b |
| c | d |
| 1 |
| 1 |
| a+b |
| c+d |
Nous allons montrer, de façon géométrique puis algébrique, que le déterminant de la matrice de transformation est le facteur de transformation de la surface : S' = S * det(A).
Démonstration géométrique :
On transforme le parallélogramme du graphique précédent en une forme de surface égale en translatant le triangle supérieur en dessous du parallélogramme, de sorte que :
S' = base * hauteur = x0 * d
où il reste à déterminer x0 en exploitant la proportionnalité des deux triangles de bases b et a-x0 :
b / d = ( a − x0 ) / c ⇔ x0 = a − b * c / d ⇒
S' = ( a − b * c / d ) * d = a * d - b * c ⇔
par (141) :
S' = det(A)
CQFD
On se rappellera déjà ici qu'à une surface correspond un produit vectoriel. On y reviendra plus loin.
Analyse de cas particuliers :
- det(A) = 1 : une rotation, dont nous avons vu que le déterminant vaut 1 (150), ne modifie pas la surface ;

- det(A) = 0 ⇔ a * d - b * c = 0 ⇔ b / d = c / a
⇔ les pentes des deux côtés du parallélogramme sont égales ⇒ la surface initiale est transformée en un segment de droite ; - det(A) < 0 : ⇔ a * d - b * c < 0 ⇔ b / d < c / a
⇔ la pente du vecteur (a,c) devient supérieure à celle du vecteur (b,d) ⇔ la surface initiale est retournée (effet miroir ⇔ surface "négative").
Démonstration algébrique :
soit la matrice| a | b |
| c | d |
ses deux colonnes représentent deux vecteurs transformés.
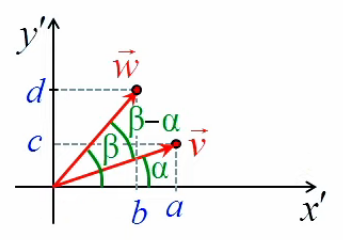
v→ =
| a |
| c |
| v * cos α |
| v * sin α |
w→ =
| b |
| d |
| v * cos β |
| v * sin β |
de sorte que :
det(A) = a * d - b * c = v * w * (sin α * cos β - cos α * sin β) ⇔ par (41) :
det(A) = v * w * sin( β - α )
or la similitude du membre de droite avec le module du produit vectoriel montre que det(A) représente bien la surface du parallélogramme déterminé par v→ et w→.
CQFD
Surface orientée. On peut maintenant interpréter la notion de surface négative comme une orientation déterminée par le signe de sin( β - α ) c-à-d par le signe de β - α (si cet angle est inférieur à 180°). Cette orientation est déterminée par la règle de la main droite : dans le graphique supra (β - α > 0) le produit scalaire est représenté par un troisième axe (z), qui sort du plan (dévissage) ; par contre si on avait β - α < 0 alors la position relative des vecteurs v→ et w→ serait inversée de sorte que l'axe z rentrerait dans le plan (vissage).
3D
Ces considérations nous conduisent à étudier le cas des volumes c-à-d à des matrices de dimension 3. Nous allons voir qu'on retrouve l'équivalent des propriétés étudiées dans le cas des matrice de dimension 2. Mais avant de poursuivre introduisons une notation rationnelle du déterminant :
det(| ux | vx | wx |
| uy | vy | wy |
| uz | vz | wz |
| ux | vx | wx |
| uy | vy | wy |
| uz | vz | wz |
Soit le système matriciel suivant :
| x' |
| y' |
| z' |
| ux | vx | wx |
| uy | vy | wy |
| uz | vz | wz |
| x |
| y |
| z |
On y retrouve les propriétés analysées pour les matrices de dimension 2, notamment que les colonnes de la matrice de transformation sont les transformées des vecteurs unitaires.
NB : le graphique ci-joint attire l'attention sur le fait que la perspective 3D est écrasée : aucun des trois vecteur dessiné n'est nécessairement dans le plan X-Y correspondant à celui de votre écran. Cette remarque facilite la lecture du graphique suivant, qui illustre l'application de la règle de la main droite dans un espace 3D.
Dans ces conditions le produit vectoriel v→ x w→ est donné par (68) :
v→ x w→ =
( vy * wz - vz * wy ) * 1→x -
( vx * wz - vz * wx ) * 1→y +
( vx * wy - vy * wx ) * 1→z
qui peut également s'écrire sous forme matricielle comme suit (69) :
v→ x w→ =| 1→x | vx | wx |
| 1→y | vy | wy |
| 1→z | vz | wz |
et dont la règle de calcul consiste à multiplier chaque vecteur de base par le déterminant 2×2 qui subsiste dans le tableau après avoir éliminé le reste de sa ligne et de sa colonne : .
Le graphique suivant montre que les composantes (v...w...− v...w...) du produit scalaire sont respectivement les aires des projections – sur les plans yz, xz et xy – du parallélogramme construit sur les vecteurs v→ et w→. La surface bleue du graphique (Syz) correspond au premier facteur du produit scalaire supra (vy * wz - vz * wy), au premier des trois déterminants ci-dessus. Enfin chacune des trois projections reproduit ce que l'on a analysé dans le cas des matrices de dimension 2.
v→ x w→ = Syz * 1→x - Sxz * 1→y + Sxy * 1→z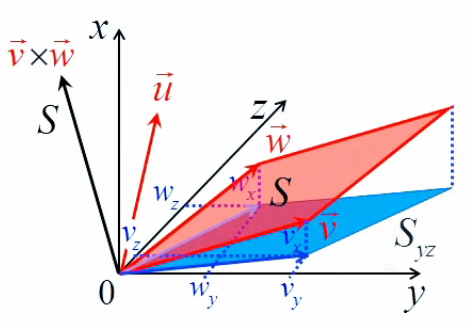
Volume. De même que le déterminant d'une matrice de dimension 2 correspond à une surface, on se doute que le déterminant d'une matrice de dimension 3 correspond à un volume, lequel est calculé par un produit mixte (70) :
det(A) = u→ . ( v→ x w→ ) ≡ volume
Démonstration :
par (58)
u→ . ( v→ x w→ ) =
|| u→|| * || v→ x w→|| * cosφ
⇔
u→ . ( v→ x w→ ) =
|| u→|| * S * cosφ = S * || u→|| * cosφ
⇔
u→ . ( v→ x w→ ) = S * h
CQFD
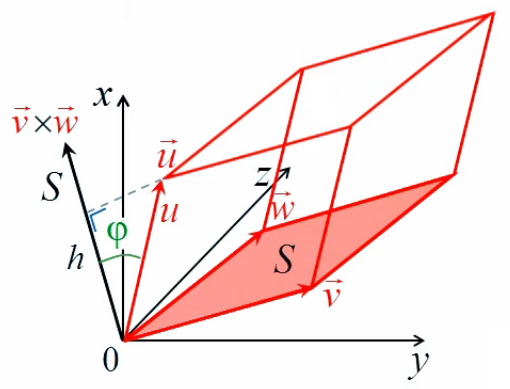
On retrouve donc une généralisation 3D de ce que l'on avait analyés en 2D : ici un cube d’arête 1 et de volume 1, dont les faces sont des carrés, est transformé en un parallélépipède non rectangle, dont les faces sont des parallélogrammes.
Analysons maintenant le déterminant. Pour ce faire exprimons ce volume en termes des composantes :
par règle de calcul du produit scalaire (68) :
v→ x w→ =
1→x * ( vy * wz - vz * wy ) -
1→y * ( vx * wz - vz * wx ) +
1→z * ( vx * wy - vy * wx ) * ⇔
par forme algébrique du produit scalaire (59) :
u→ . ( v→ x w→ ) =
ux * ( vy * wz - vz * wy ) -
uy * ( vx * wz - vz * wx ) +
uz * ( vx * wy - vy * wx ) ⇔
en reprenant la notation mnémonique :
| ux | vx | wx |
| uy | vy | wy |
| uz | vz | wz |
où le membre de droite est noté det(A).
Volume orienté.. Il ressort de :
u→ * ( v→ x w→ ) =
|| u→|| * || v→ x w→|| * cos(φ)
(152)
que det(A) > 0 si cos(φ) > 0 ⇔ 0 ≤ φ < π/2 ce qui dans le graphique précédent correspond à un trièdre (v→,w→,u→) dextrogire (le produit scalaire v→ x w→ va dans le sens de u→). À l'opposé, dans le graphique ci-dessous on a inversé v→ et w→ ⇒ le produit scalaire v→ x w→ ne va plus dans le sens de u→ (trièdre lévogyre), ce qui correspond à π/2 < φ ≤ π. Enfin det(A) = 0 si cos(φ) = 0 ⇔ φ = π/2, c-à-d que les trois vecteurs sont coplanaires ⇔ le volume est bien nul.
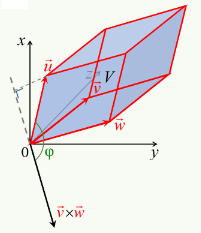
On notera enfin que :
u→ * ( v→ x w→ ) =
ux * ( vy * wz - vz * wy ) -
uy * ( vx * wz - vz * wx ) +
uz * ( vx * wy - vy * wx )
est la somme de trois volumes :
u→ * ( v→ x w→ ) =
ux * Syz -
uy * Sxz +
uz * Sxy
4D
Pour développer la notion de matrice de dimension n, on va commencer par étudier la matrice de dimension 4. Mais avant, il nous faire une parenthèse pour souligner le fait que la notion de déterminant ne fait sens qu'avec des matrices carrées. Pour ce faire rappelons-nous l'équivalence des égalités suivantes :
a * x + b * y = x'c * x + d* y = y'
⇔
(a, b) . (x, y) = x'
(c, d) . (x, y) = y'
⇔
| a | b |
| c | d |
| x |
| y |
| x' |
| y' |
⇔
| x |
| y |
| d | -b |
| -c | a |
| x' |
| y' |
⇔
| x |
| y |
| x' |
| y' |
Or il est facile de vérifier que si A n'est pas carrée alors le système d'équation correspondant est soit sous-déterminé (# de variables > # d'équations) soit sur-déterminé (# de variables < # d'équations).
Cette précision étant faite notons l'impossibilité de représenter un espace à 4 dimensions, raison pour laquelle dans le graphique ci-contre le 4° axe et le 4° vecteur sont représentés en hachuré.
Heureusement la notation mathématique n'est pas limitée par cette contrainte.
Ainsi le cas 3D, det(A) =
u→ . ( v→ x w→ )=
ux *
| vy | wy |
| vz | wz |
| vx | wx |
| vz | wz |
| vx | wx |
| vy | wy |
=
ux * Syz - uy * Sxz + uz * Sxy
devient
r→ . ( u→ x v→ x w→ )=
rt *
| ux | vx | wx |
| uy | vy | wy |
| uz | vz | wz |
| ut | vt | wt |
| uy | vy | wy |
| uz | vz | wz |
| ut | vt | wt |
| ux | vx | wx |
| uz | vz | wz |
| ut | vt | wt |
| ux | vx | wx |
| uy | vy | wy |
=
rt * Vxyz - rx * Vtyz + ry * Vtxz - rz * Vtxy
Cette somme étant composée de 4 volumes de dimension 4, on entre ainsi dans le domaine des hypervolumes (dimension > 3), et en l'occurrence dans celui des parallélotopes.
Où l'on voit apparaître une structure de calcul en poupées russes (cf. les "mineurs" du déterminant). Le nombre d'opération est ici de 63, de sorte que le calcul global est très lourd. Nous verrons des méthodes permettant de simplifier de nombreux cas de calcul.
nD
On peut maintenant généraliser au cas de matrices de dimension nxn. Notons que l'analogie est (évidemment) elle aussi limitée pour représenter des dimensions supérieures à trois : ainsi un matrice de niveau n contient n matrice de niveau n-1 (alors qu'une poupée russe n'en contient qu'une seule), de sorte que le nombre de poupées c-à-d de déterminants vaut N!, le dernier étant de dimension 1x1.

det(A) = v→1 . ( v→2 x v→3 x ... x v→N )
Formule générale du déterminant et cofacteur
Le déterminant de la matrice 3x3 (153) est une somme de 6 produits de 3 facteurs :
ux * ( vy * wz - vz * wy ) -
uy * ( vx * wz - vz * wx ) +
uz * ( vx * wy - vy * wx ) =
ux * vy * wz - ux * vz * wy - uy * vx * wz + uy * vz * wx + uz * vx * wy - uz * vy * wx
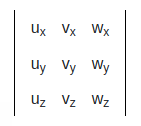
3 colonnes u,v,w
3 lignes x,y,z
Cette somme de produits est telle que :
- les facteurs des produits correspondent aux trois colonnes (u,v,w) du déterminant ;
- les indices (x,y,z) des facteurs correspondent aux trois lignes, et ne se répètent jamais au sein de chaque facteur (puisque chaque mineur (*) est déterminé en éliminant la ligne et la colonne de son élément de référence) ;
(*) C-à-d les "poupées russes" évoquées supra, étant entendu qu'à la différence des poupées russes, un mineur de niveau n contient n mineurs de niveau n-1.
Il en résulte que le déterminant d'ordre n contient toutes les combinaisons possibles de n éléments distincts appartenant à des lignes et des colonnes différentes. Et il apparaît que les éléments de la somme supra sont donc les combinaisons que l'on peut obtenir de 3 lettres (x,y,z), leur nombre est donné par Anp = n ! / ( n - p ) !(121) soit ici 3!/(3-3)=6.
On voit également qu'il y a une forme de symétrie, inhérente au caractère carré de la matrice et au mode de calcul du déterminant. Il résulte de cette symétrie que le calcul du déterminant peut être réalisé à partir de n'importe quelle colonne ou ligne. La difficulté dans ce type de calcul est de ne pas se tromper dans l'attribution des signes moins (résultant de la règle de la main droite).

Pour cela il suffit de constater que cette répartition est elle aussi symétrique, la règle étant celle du damier : dans l'image ci-contre les cases grisées correspondent aux signes négatifs, et l'on notera qu'elles correspondent également à une somme d'indices (ligne+colonne) impaire, ce qui est exprimé par (−1) i+j dans la la formulé générale du calcul de déterminant :
det(A) = ∑ iouj=1N (−1) i+j * aij * Mijoù
• Mij est le mineur correspondant à l'élément aij, c-à-d déterminé par la suppression de la colonne et de la ligne de aij (il porte donc les indices de son référentiel) ;
• iouj=1 signifie que le calcul peut être effectué sur n'importe quelle ligne i ou colonne j.
Que l'on simplifie encore par :
det(A) = ∑ iouj=1N aij * Cijoù Cij = (−1) i+j * Mij est le "cofacteur" de l'élément aij.
Ainsi, appliquée à partir de la première ligne, cette définition donne :
det(A) = ∑ j=1N a1j * C1j
Le déterminant d'une matrice est donc la somme des produits des éléments d'une rangée quelconque par leur cofacteur. En pratique, pour simplifier le calcul d'un déterminant, on le calculera sur base de sa ligne ou colonne contenant le plus de zéros.
Propriétés du déterminant
On va étudier ici le cas de trois type de matrice : transposée, permutée et proportionnelle. Nous verrons qu'en combinant les propriétés de ces matrices particulières avec la propriété générale de linéarité on peut simplifier le calcul des déterminants.
Matrice
transposée
Soit la matrice A telle que : [A]ij = aij, alors sa transposée est telle que [At]ij = aji. La transposée est donc une symétrie axiale autour de la première diagonale.

Dès lors qu'un déterminant peut être calculé selon n'importe quelle ligne ou colonne, il en résulte que :
det ( At )ij = det ( A )ij
Ces deux matrices correspondent à des parallélépipèdes de formes différentes (puisque les vecteurs sont différents) mais de volumes identiques (puisque les déterminants sont égaux).
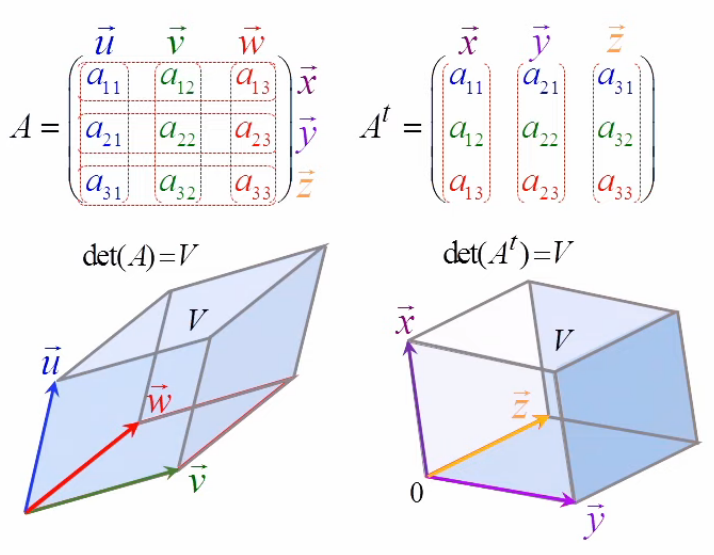
Matrice
permutée
Une matrice est permutée si deux rangées parallèles (lignes ou colonnes) sont permutées. Géométriquement, la permutation de deux colonnes correspond à la permutation des vecteurs correspondants ⇒ la règle de la main droite montre que cette permutation change le signe du déterminant.
det(A) = u→ . ( v→ x w→ ) = V ⇔ en permuttant v→ et w→ :det(A') = u→ . ( w→ x v→ ) = -V ⇔ en permuttant u→ et w→ :
det(A'') = w→ . ( u→ x v→ ) = V ⇔ ...
Étant donné qu'une matrice et sa transposée ont le même déterminant, il en résulte qu'on observera le même phénomène que ci-dessus dans le cas de permutations de lignes :
soit : B = At ⇒ det(B) = det(A) = Vsoit : B' = A't ⇒ det(B') = det(A') = -V
etc.
Ainsi en règle générale, après n permutations de rangées parallèles (colonnes ou lignes) le déterminant est multiplié par (−1)*n : det ( A (n) ) = (-1) n * det ( A )
Matrice
proportionnelle
Une matrice est dite proportionnelle si elle a au moins deux rangées (lignes ou colonnes) proportionnelles. Étudions le cas du calcul du déterminant d'une matrice proportionnelle relativement à une rangée non proportionnelle. Or on vérifie facilement que, étant donné le mode de calcul des déterminants, les mineurs impliquant les deux rangées proportionnelles sont nécessairement nuls, et donc le déterminant de la matrice aussi. Et ce principe vaut pour toute matrice de degré n : la nullité des mineurs de dernier niveau se répercutant dans tous les niveaux de la "poupée russe" du calcul du déterminant. Le graphique suivant illustre l'interprétation géométrique : le "plan" déterminé par les deux vecteurs proportionnels w→=α*v→ est ramené à une droite, et donc le volume à un plan ⇒ le volume est nul, et le volume c'est le déterminant. On a donc que :
le déterminant d'une matrice proportionnelle est nul
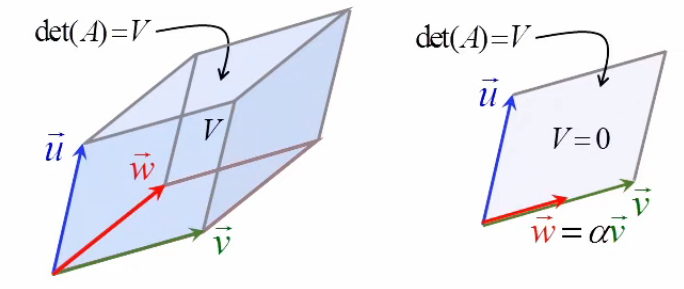
Linéarité
Cette quatrième propriété est la plus importante car elle permet de simplifier le calcul matriciel (c-à-d du calcul de déterminants). Par "linéarité" on entend ici que si tous les éléments d’une seule rangée (ligne ou colonne) d’un déterminant sont multipliés par une constante, alors la valeur de ce déterminant (et donc le volume) est aussi multipliée par cette constante :
Soit la matrice A telle que :
det(A) = u→ . ( v→ x w→ ) = V
alors
det(A') = α * u→ * ( v→ x w→ ) = α * V
Pour démontrer cette propriété spécifiquement au cas d'une ligne ou d'une colonne on utilisera :
det(A) = ∑ iouj=1N aij * Cij
(154)
⇒ appliquons-la, par exemple, relativement à la première ligne :
det(A) = ∑ j=1N a1j * C1j ⇒
det(A') = ∑ j=1N α * a1j * C1j = α * ∑ j=1N a1j * C1j = α * det(A)
CQFD
Somme de déterminants. Il découle de la propriété de linéarité que det(A+B) ≠ det(A) + det(B).
Démonstration :
Soit les matrices :
• A telle que : det(A) = u→ . ( v→ x w→ ) = V
• A' = α * A
alors
det(A') = α * u→ . [ ( α * v→ ) x ( α * w→ ) ] = α 3 * u→ . ( v→ x w→ ) = α 3 * det(A) ⇒
det(α * A) = α N * det(A) ≠ α * det(A)
NB : on voit ici qu'il n'y a plus linéarité dès que plus d'une rangée est multipliée par une constante.
⇒ soit α=2 :
det(A+A) ≠ det(A) + det(A) ⇒
det(A+B) ≠ det(A) + det(B)
Méthode de calcul. Soit :
det(A') = 2 * u→ . ( v→ x w→ ) = 2 * V ⇔
det(A') = ( u→ + u→ ) . ( v→ x w→ ) = 2 * V ⇔
det(A') = u→ . ( v→ x w→ ) + u→ . ( v→ x w→ ) = V + V
⇒
det(A') = ( u→ + s→ ) . ( v→ x w→ ) = Vu + Vs ⇔
det(A') = u→ . ( v→ x w→ ) + s→ . ( v→ x w→ ) = Vu + Vs
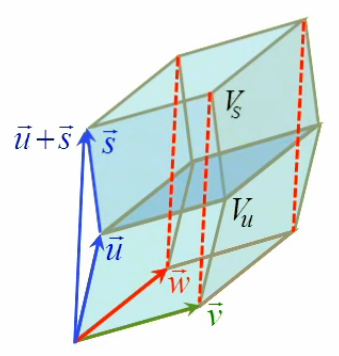
Ainsi le volume du parallélépipède déterminé par les lignes hachurée en rouge est égal à Vu + Vs ⇔ det( A' ) = det( Au ) + det( As ), que l'on démontre trivialement à partir de det(A) = ∑ iouj=1N aij * Cij
(154) :
∑ i=1N ( ai1 + a'i1 ) * Ci1 =
∑ i=1N ai1 * Ci1
+
∑ i=1N a'i1 * Ci1

Pour élaborer notre technique de simplification du calcul de déterminant, on va poser s→ = v→. Or dans ce cas det(As)=0 par (156). Ainsi si l'on remplace la première colonne par la somme de celle-ci avec la seconde, on conserve le même déterminant.
Et si l'on pose plutôt s→ = α * v→ + β * w→ on obtient toujours le même résultat induit pas (156) : le déterminant reste inchangé ! Et c'est grâce à cela que l'on va pouvoir simplifier des déterminants. L'idée est de chercher des combinaisons linéaires qui permettent de simplifier le déterminant que l'on souhaite calculer, c-à-d d'obtenir des zéros dans la rangée modifiée (ligne ou colonne).
Ainsi dans l'exemple suivant on a pu transformer la matrice en une matrice triangulaire, dont le déterminant vaut tout simplement le produit des éléments de la diagonale !
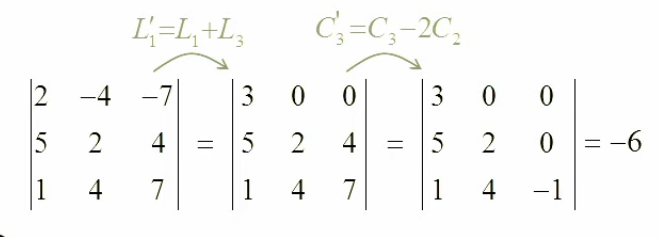
Matrice inverse
Nous allons ici étudier la formulation générale de la formule du déterminant :
A-1 = 1 / det(A) *| d | -b |
| -c | a |
Cette dernière est très pratique (facile à retenir) pour A2x2, mais plus pour des dimensions supérieures. On va donc tenter de trouver la forme générale de :
| d | -b |
| -c | a |
Illustration
La résolution de nombreux calculs d'ingénierie requiert l'utilisation de l'inverse d'une matrice. C'est par exemple le cas de l'évaluation (par simulation informatique) des effets des forces aérodynamiques sur la structure d'un avion (évaluation de sa déformabilité).
Ainsi dans le modèle matriciel A * X = F :
• la matrice F décrit les forces aérodynamiques ;
• la matrice A décrit la structure matérielle de d'avion ;
• la matrice X décrit les déformations imprimées à la structure de l'avion (A) par les forces aérodynamiques (F).
L'égalité exprime la troisième loi de Newton (ou principe d'action-réaction) (169) ⇒ pour connaître l'ampleur des déformations de la structure (c-à-d X) il faut exprimer X en fonction des valeurs connues que sont les forces aérodynamique (F) et la résistance du matériau constituant la structure de l'avion (A) ⇔ X = A-1 * F
Pratiquement la modélisation de l'avion se fait sous forme de points appelés "noeuds" (de sorte que ce type de modélisation est appelé "procédure de discrétisation"). Il s'agit alors d'évaluer la déformabilité (X) du modèle d'avion à partir des valeurs connues que sont la déformabilité du matériaux constituant la structure (A) et les forces aérodynamiques (F).
Calcul
Trouver la matrice A-1 c'est trouver la matrice A-1 telle que A-1 * A = I. Pour ce faire on va nommer les constituants de A-1 de telle sorte que ses trois lignes représentent trois vecteurs, associés au vecteurs de A, par transposition et notation majuscule (nous verrons plus loin pourquoi).
Or nous avons vu que le produit matriciel se calcule comme suit : l'élément i j de la matrice produit C=A*B est égal au produit scalaire de la ligne i de A par la colonne j de B (144). Et l'on voit dans l'égalité ci-dessus que :
- 1° ligne de I : U→ doit être perpendiculaire à v→ et w→ car : U→ . v→ = U→ . w→ = 0 (61)
- 2° ligne de I : V→ doit être perpendiculaire à u→ et w→ car : V→ . u→ = V→ . w→ = 0
- 3° ligne de I : W→ doit être perpendiculaire à u→ et v→ car : W→ . u→ = W→ . v→ = 0
Or pour obtenir ces doubles perpendicularités il suffit de poser que :
- U→ est produit vectoriel de v→ et w→ : U→ = v→ x w→ (62)
- V→ est produit vectoriel de w→ et u→ : V→ = w→ x u→
- W→ est produit vectoriel de u→ et v→ : W→ = u→ x v→
... ce qui implique que chaque élément de la diagonale de la matrice du membre de droite devrait être égal à det(A) :
- U→ . u→ = ( v→ x w→ ) . u→ = det(A)
- V→ . v→ = ( w→ x u→ ) . v→ = det(A)
- W→ . w→ = ( u→ x v→ ) . w→ = det(A)
En effet nous avons vu que le déterminant correspond au volume déterminé par ses vecteurs, et qu'on le calcule par le produit mixte de ceux-ci (152). Ce produit mixte peut évidemment être calculé dans tous ses ordres.
Or l'on devrait avoir U→ * u→ = V→ * v→ = W→ * w→ = 1. Par conséquent la matrice faite des vecteurs lignes n'est pas A-1 mais det(A)*A-1 (⇒ après mise en évidence de det(A) dans le membre de droite, puis élimination dans les deux membres on retrouve bien A-1 * A = I).
Il reste donc à calculer les éléments de la matrice det(A)*A-1. Pour ce faire on va utiliser le fait que ces trois vecteurs lignes ont été définis supra comme étant trois produits vectoriels. Ainsi pour la première ligne on a par (69) :
U→ = v→ x w→ =| 1→x | vx | wx |
| 1→y | vy | wy |
| 1→z | vz | wz |
dont la composante en x, c-à-d l'élément Ux de la matrice det(A)*A-1, est par (68) le cofacteur de 1→x dans le déterminant ci-dessus :
Ux =| vy | wy |
| vz | wz |
que l'on retrouve dans la matrice A comme cofacteur de ux.
On peut alors généraliser par la constatation suivante : les composantes de chaque vecteur ligne de la matrice det(A)*A-1 (majuscules) sont les cofacteurs des éléments de la colonne correspondante de A (minuscules).
Uy = -
| vx | wx |
| vz | wz |
On va alors construire la matrice des cofacteurs de la matrice A, notée CA, et qui est la matrice A dont les éléments minuscules sont remplacés par les éléments majuscules de det(A)*A-1, de sorte que det(A) * A-1 = CAt ⇔
A-1 = CAt / det(A)
dont on constate, à partir de (154), que c'est une généralisation de (143).
Déterminant d'un produit de matrices
Soient les matrices A et B ⇒ par (154) :
det(A) = ∑ i,j =1N aij * CijA
det(B) = ∑ i,j =1N bij * CijB
⇒
det(A*B) =
∑ i,j =1N ( ∑ k=1N aik * bkj ) * CijAB =
det(A) * det(B)
La démonstration de l'égalité entre le membre de gauche et celui de droite par développement du membre central est trop complexe algébriquement. C'est pourquoi on va se limiter ici à une interprétation géométrique (à deux dimensions, mais que l'on peut facilement généraliser). Cette interprétation sera l'occasion de résumer l'essentiel de la matière que nous venons de développer au sujet du calcul matriciel.
Une matrice de dimension 2 (c-à-d 2x2) peut être vue comme représentant la transformation d'une surface dans le plan de coordonnées cartésiennes.
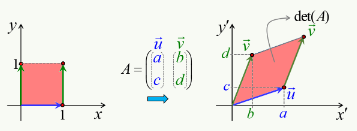
Cette transformation est telle que :
- les vecteurs unitaires 1→x de coordonnées (1,0) et 1→y de coordonnées (0,1), qui représentent un carré, sont transformés en deux vecteurs u→ de coordonnées (a,c) et v→ de coordonnées (b,d), qui représentent un parallélogramme ;
- les cordonnées de ces deux vecteurs constituent les deux colonnes de la matrice de transformation ;
- le déterminant représente la surface de l'aire transformée, et par conséquent le facteur par lequel l’aire du carré unitaire est multipliée pour donner l’aire du parallélogramme.
| a | b |
| c | d |
| x |
| y |
| x' |
| y' |
il suffit de remplacer (x,y) par (1,0) pour obtenir que a*1+b*0=a et c*1+d*0=c :
| a | b |
| c | d |
| 1 |
| 0 |
| a |
| c |
et de remplacer (x,y) par (0,1) pour obtenir que a*0+b*1=b et c*0+d*1=d :
| a | b |
| c | d |
| 0 |
| 1 |
| b |
| d |
ou encore de remplacer (x,y) par (1,1) pour obtenir que a*1+b*1=a+b et c*1+d*1=c+d :
| a | b |
| c | d |
| 1 |
| 1 |
| a*1+b*1 |
| c*1+d*1 |
| a+b |
| c+d |
| a |
| c |
| b |
| d |
Où l'on voit que le point (1,1), correspondant à une surface égale à 1, a été transformée en le vecteur somme u→+v→ correspondant au point de coordonnées (a+b, c+d), et à une surface égale à det(A).
De la même manière on peut remplacer (1,1) par (x,y), pour formuler la transformation du point (x, y), correspondant à une surface rectangulaire x * y, en un point (a*x+b*y, c*x+d*y), correspondant à une surface parallélépipédique x * y * det(A) :| a | b |
| c | d |
| x |
| y |
| a*x+b*y |
| c*x+d*y |
| a*x |
| c*x |
| b*y |
| d*y |
| a |
| c |
| b |
| d |
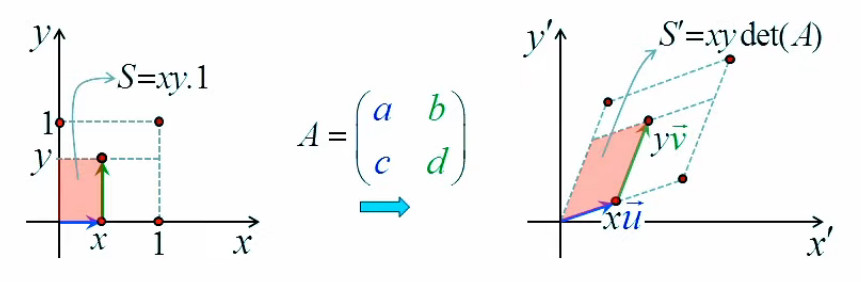
N.B. Il est donc erroné de dire que "le déterminant, c'est la surface" : cela n'est vrai que si la surface originelle vaut 1. En fait le déterminant c'est le facteur de transformation de la surface. La généralisation ci-dessus montre bien qu'on passe d'une surface x*y à une surface x*y*det(A).
Et l'on peut étendre cette généralisation à toute surface ε2 dont l'origine est (x,y), et qui est donc transformée en une surface ε2 * det(A) d'origine ( a * x + b * y , c * x + d * y ).
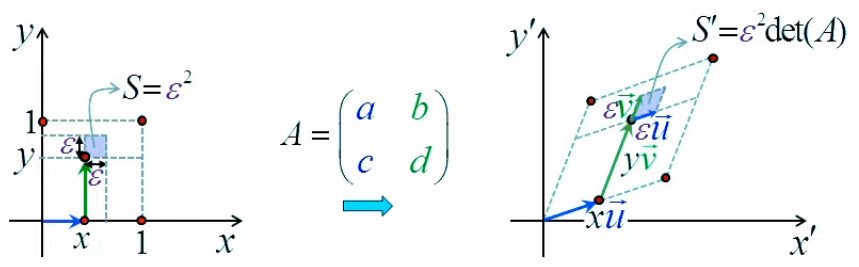
Et l'on peut encore étendre la généralisation à toute aire composée de petits carrés de surface ε2.
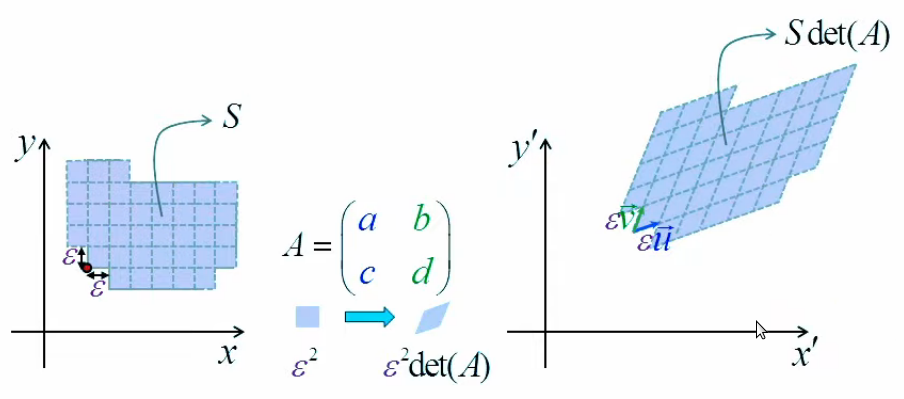
Comme en outre on peut abaisser la valeur de ε à un niveau arbitraire, on peut donc dessiner n'importe quel surface, y compris avec des contours "arrondis". Enfin la généralisation peut s'étendre à des volumes de dimension N.
Et comme le produit matriciel B*A correspond à l'application de la transformation par B à la transformation par A (148) :
S=1 ⇒
SA = 1 * det(A) ⇒
SBA = det(A) * det(B)
or :
det(B*A) = SBA ⇒
det(B*A) = det(B) * det(A)
CQFI.
En particulier si :
B=A-1 ⇒
det(A-1*A) = SA-1A = det(A-1) * det(A) ⇔
det(I) = det(A-1) * det(A) ⇔
det(A-1) = 1 / det(A) = det(A)-1
ou encore, si :
B=A ⇒
det(A*A) = SAA = det(A) * det(A) ⇔
det(A2) = det(A) * det(A) ⇔
det(A2) = det(A)2