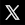VII. Action ''à distance''
Électricité
2. Force électrique (loi de Coulomb)
3. Champ électrique
Applications techniques
Nous avons évoqué les mécanismes notamment microscopiques de l'électricité. Ce phénomène peut être facilement observé à l'échelle humaine en frottant un objet de cuivre (forte affinité aux électrons c-à-d forte propension à les attirer) avec un chiffon de coton (faible affinité), ce qui va séparer les charges positives des charges négatives, et ainsi provoquer un transfert d'électrons du chiffon vers le cuivre. Le premier étant ainsi chargé positivement (puisqu'il a perdu des électrons à partir d'une situation de charge neutre) et le second négativement (puisqu'il a gagné ces électrons à partir d'une situation de charge neutre) une force d'attraction apparaît entre les deux au point que le chiffon peut rester collé à l'objet de cuivre. Ce phénomène est appelé "électrisation".
Ce bloc de cuivre forme un réseau cristallin, comme le NaCl, mais avec cette différence que la cohésion de ce cristal de cuivre est formé par la mise en commun des électrons périphériques, plutôt que par un transfert d'électrons (Na --> Cl : cf. supra #ions) : les électrons périphériques de chaque atome de Cu circulent librement entre ceux-ci, en exerçant ainsi un rôle de "colle" entre les atomes de cuivre, et en faisant de ce métal un bon "conducteur" (contrairement au bois ou au plastique, qui sont ainsi de bons isolants).
Claquage. Si le nombre de ces électrons "injectés" par l'électrisation devient très élevé, alors les forces de répulsion entre électrons peuvent avoir pour effet d'en éjecter. On observe alors un "claquage électrique" formant un "arc électrique", communément appelé "éclair".
Plasma. L'image ci-dessus est celle d'un lampe à plasma : la boule métallique baigne dans un gaz à l'état de plasma (ce qui ralentit l'effet de claquage). Un plasma est un état de la matière dans lequel les atomes ont perdu leurs électrons, de sorte qu'ils circulent au gré des forces qu'ils rencontrent. Nous avions évoqué le plasma dans la formation des étoiles et de la matière après le "big bang" (cf. #plasma). Des plasmas sont développés pour étudier le phénomène de fusion nucléaire.
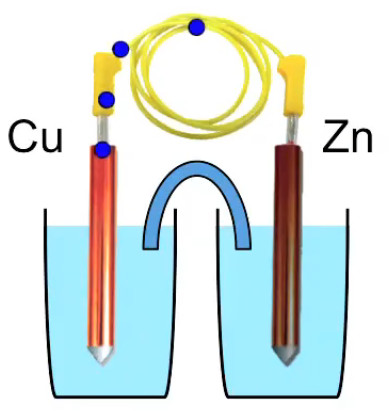
Le bâton cuivre est plongé dans une solution de sulfate de cuivre, et le bâton de zinc dans une solution de sulfate de zinc.
Une notion importante est "l'affinité" pour les électrons : ainsi on peut créer un courant électrique passant d'un bloc de zinc vers un bloc de cuivre, car l'affinité électronique du zinc est faible tandis que celle du cuivre est élevée (on peut dire aussi que les électrons sont plus attirés par le cuivre que par le zinc). C'est le principe de la pile, illustré dans l'image ci-contre (et que nous étudierons plus en détail dans le chapitre consacré au potentiel : nous verrons notamment pourquoi une pile s'épuise, mettant ainsi un terme au courant permanent qui y circulait).
Courant
Dans la plupart des centrales électriques on créé du courant électrique grâce à une propriété importante des aimants : quand des électrons passent dans le champ magnétique généré par un aimant leur trajectoire est déviée par une force magnétique perpendiculaire (électromagnétisme). Ainsi en faisant tourner des aimants autour d'un bobine de conducteur, on y créé un courant électrique. Ainsi une force mécanique (le rotor) créé de la force électrique par l'intermédiaire de la force magnétique [pour approfondir revoir l'illustration supra du produit vectoriel par la force de Lorentz (64)].
Les applications de courant électrique sont très nombreuses. En voici d'autres.
-
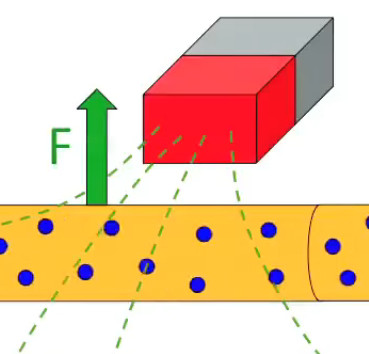
Le moteur électrique c'est en quelque sorte l'inverse de la centrale électromagnétique : on fait passer un courant électrique au travers d'un câble baigné dans un champ magnétique, ce qui pousse vers le haut les électrons, et donc le câble dans lequel ils circulent. Un mécanisme peut alors exploiter ce mouvement du câble pour faire tourner un rotor, transformant ainsi une force électrique en force mécanique par l'intermédiaire de la force magnétique.
- En faisant passer un flux d'électron ("courant électrique") au travers d'un fil de cuivre, ces électrons bousculent les atomes de cuivres provoquant ainsi leur mouvement, ce qui génère de la chaleur (radiateur électrique) ; au-delà d'une certaine température le fil de cuivre va chauffer à blanc c-à-d émettre de la lumière (ampoule électrique) ;
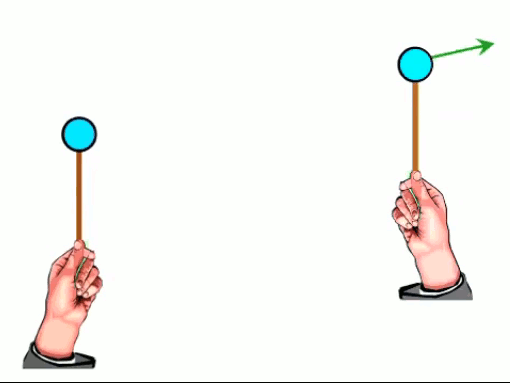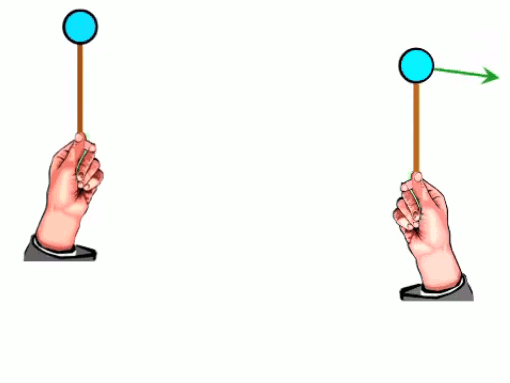
Dans l'animation ci-contre, la boule de gauche est chargée positivement et la boule de droite négativement ⇒ la première exerce une force répulsive sur la seconde. Si en outre la première effectue des mouvements de bas en haut, ceux-ci sont alors communiqués à la boule de droite. La force électromagnétique exercée par la première sur la seconde devient ainsi une onde électrique. C'est le principe de l'antenne : un mouvement de va et vient des électrons, généré le long de l'antenne émettrice, est transporté vers les électrons de l'antenne réceptrice.
Force électrique (loi de Coulomb)
Forme
scalaire
La loi de Coulomb décrit la force électrique exercée entre deux charges q1 et q2 séparées par une distance r :
F(r) = kC * q1 * q2 / r 2
où kC est la constante de Coulomb.
On notera la similitude avec la loi de gravitation universelle (que Coulomb connaissait), qui décrit la force de gravitation FG = G * m1 * m1 / r 2 (251), mais dont la constante de gravitation G est énormément plus petite que kC (la force électrique est beaucoup plus forte que la force gravitationnelle).
Coulomb se doutait que les grandeurs intervenant dans le calcul de F(r) étaient q1, q2, r et une constante. Il a pu déterminer (202) expérimentalement grâce à la balance à torsion.
Coulomb a ainsi pu mesurer que la force électrique (répulsive ou attractive) diminue avec le carré de la distance entre les corps chargés sur lesquels elle s'exerce :
F(r) = A / r 2
Ensuite il a mesuré, pour une distance r et une charge q2 données, le rôle joué par la charge q1 électrique sur la force électrique. Coulomb a ainsi observé une relation proportionnelle ⇒ il faut remplacer A par B*q2 :
F(r) = B * q2 / r 2
Mais en vertu du principe de conservation, la force, qu'elle soit répulsive ou attractive, est identique pour les deux charges q1 et q2 ⇒ il faut remplacer B par k*q1 :
F(r) = k * q1 * q2 / r 2
N.B. Le produit des charges est cohérent avec la propriété, à priori peu intuitive, de superposition de la force électrique : dans le graphique suivant la force électrique exercée par les trois protons de gauche ne se répartit pas sur les deux de droite, mais s'applique à chacun d'eux. Et cela on ne retrouve bien dans :
kC * 3qe * 2qe / r 2 = 6 * kC * qe2 / r 2

Le principe de superposition signifie donc que l'effet d'une charge q1 sur une charge q0 n'est pas influencé par l'effet d'une charge q2 sur la charge q0.
Enfin si une des deux charges est négative, alors il en de même de F(r), qui est bien alors une force d'attraction, en cohérence avec l'algèbre de l'électricité (cf. supra #algebre-electricite).
Quelle est l'unité (ou "dimension") [ kC ] de kC ? Si l'on écrit l'équation (202) en remplaçant tout par les dimensions on obtient :
N = [ kC ] * C2 / m2 ⇔
[ kC ] = N * m2 / C2 ⇒
Quelle est la valeur de kC ? Si q1=q1=1C et r=1m ⇒ on observe expérimentalement que F=8,99*109N ⇒ par (202) on en déduit que kC = 8,99 * 109 N * m2 / C2
C'est une valeur énorme au regard de la charge d'un électron qe = 1,6 * 10 -19 C ⇒ si l'on devait charger une bille de 10cm à 1C il y aurait tellement d'électrons dans cette bille que l'on observerait de très nombreuses expulsions d'électrons (éclairs). Si l'unité de charge qu'est le coulomb (C) est si grande, c'est parce qu'elle a été conçue dans le cadre de la force magnétique.
Vecteur
unitaire
radial
L'équation (202) n'est que la forme scalaire de la force électrique, et est donc incomplète. Il convient de pouvoir déterminer la direction dans laquelle la force s'exerce ⇒ il faut passer de la forme scalaire à la forme vectorielle. Pour ce faire il suffit de multiplier la forme scalaire par un vecteur unitaire, noté 1→r (ou encore u→r ou e→r selon les auteurs) : par (57) :
F→ = F * 1r→
où 1r→ est appelé vecteur unitaire radial.
(cf. fin de section pour justification du terme "radial")
⇒ par (202) :
F→ = kC * q2 * q1 / r 2 * 1r→
Comment calculer ce vecteur unitaire ? L'axe des forces électriques agissant sur les charges q1 et q2 passe par ces deux charges (leur centre de gravité). Or, par , le vecteur reliant celles-ci correspond à la définition de la différence de leurs vecteurs positions r→1 = (x1, y1, z1) et r→2 = (x2, y2, z2).
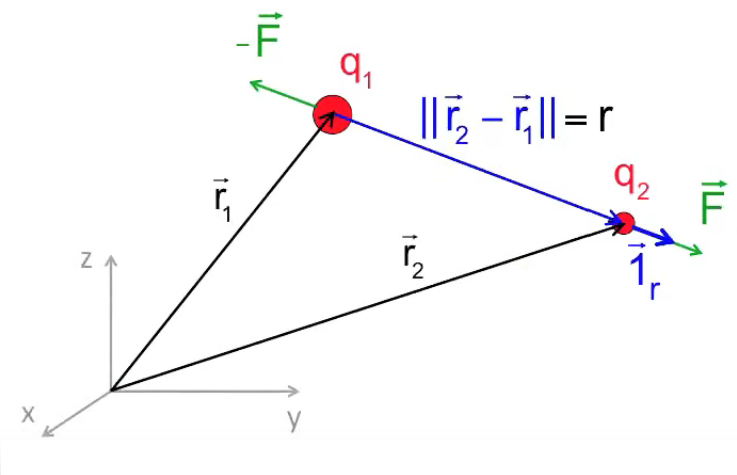
Par conséquent, la distance r entre les deux charges, c'est la norme du vecteur différence :
r = || r2→ - r1→ ||
Par conséquent, le vecteur unitaire par lequel on va multiplier F→ c'est bien 1→r. Celui-ci est défini par (57) :
1→r = r→ / || r→ || ⇔
1r→ = ( r2→ - r1→ ) / || r2→ - r1→ || ⇔ par (52) et (51) :
1r→ = ( x2 - x1 , y2 - y1 , z2 - z1 ) / √ ( ( x2 - x1 ) 2 + ( y2 - y1 ) 2 + ( z2 - z1 ) 2 )
qui est donc le vecteur direction (en norme) de la force exercée en q2 ; ce vecteur est sans dimension (m/m=1).
N.d.A. En vertu du principe d'action-réaction (169), tout le raisonnement ci-dessus peut se faire arbitrairement par rapport à q1 ou q2. D'autre part, en restant ci-dessus dans le cas de la force F→ exercée sur q2, on a que :
- F→ =
kC * q2 * q1 / r 2 * - 1r =
kC * q2 * q1 / r 2 * ( r→1 - r→2 ) / || r→1 - r→2 || =
kC * q2 * q1 / r 2 * ( r→1 - r→2 ) / r =
kC * q2 * q1 / r 2 * - ( r→2 - r→1 ) / r
Application. Soit :
• q1= -2C ; q2= 1C
• r→1 = (0, 0, -1)m
• r→2 = (0, 4, 2)m
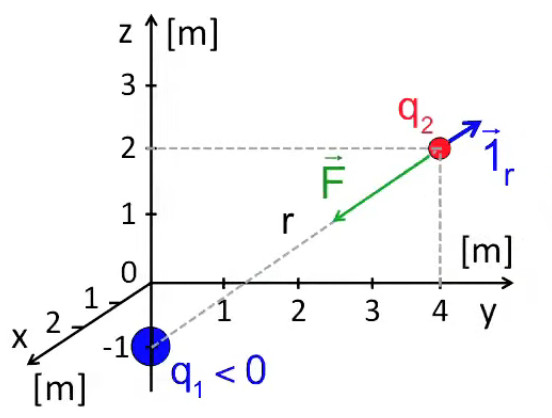
⇒
r→2 - r→1 = (0, 4, 3)
|| r→2 - r→1 || = √(42 + 32) = 5
⇒
1r = (0, 4, 3) / 5 = (0, 4/5, 3/5) ⇒
F→ = 8,99 109 * 1 * -2 / 52 * (0, 4/5, 3/5) N ⇔
F→ = (0, -0,58, -0,43) GN
NB : les signes des charges n'ont pas d'effet sur le vecteur unitaire, qui est donc indépendant de la nature attractive ou répulsive de la force.

Vecteur unitaire radial. Le vecteur unitaire 1→r est qualifié de "radial" (d'où l'indice "r") car si l'on déplace l'une des deux charges autour de l'autre, la force décrit le cercle correspondant. Le caractère radial du vecteur unitaire dans la loi de Coulomb est à la base de la notion de champ de forces électriques. Poursuivons donc notre cheminement : Coulomb scalaire ⇒ Coulomb vectoriel ⇒ champ de forces ...
Champ électrique
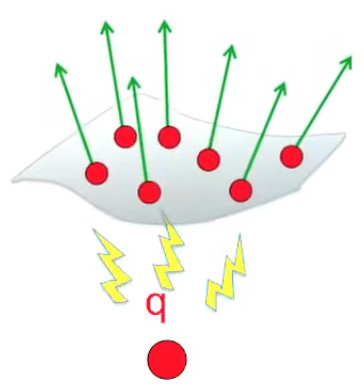
Lévitation d'une feuille de papier chargée.
Si je soulève un feuille de papier non rigide à l'aide d'une tige placée en travers d'elle et à égale distance des deux bords, les deux parties non soutenues par la force mécanique de la tige sont ballantes (N.d.A. : sauf si l'expérience est réalisée en apesanteur). Par contre si cette feuille est suffisamment électrisée elle pourra être maintenue en sustentation sur toute sa surface. On dit alors qu'elle subit un "champ de forces" (électriques).
Ainsi la force électrique se distingue de la force mécanique notamment par deux propriétés :
- la force électrique s'exerce à distance
- la force électrique s'exerce sur l'ensemble d'un corps, alors que la force mécanique s'exerce sur des points d'application, et c'est précisément cette action d'ensemble qu'exprime la notion de champ électrique, via la notion de radialité.
La notion de "radialité" du vecteur unitaire est donc inhérente au champ électrique. Pour modéliser ce phénomène d'action d'ensemble à distance, on va accentuer la différenciation entre q1 et q2, qui deviennent q et q0. Cette dernière est appelée "charge d'essai", pour illustrer une multitude de positions relativement à q, de sorte que la variation du vecteur r0→ - rq→ dans l'espace décrit un volume centré sur q : le champ électrique.
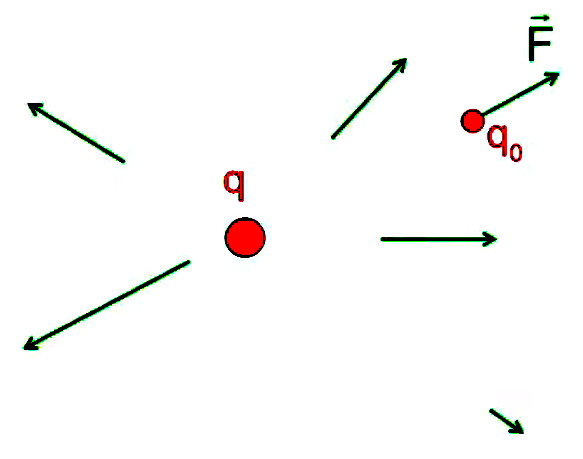
Pour définir le champ électrique E→ correspondant à la charge q, il faut donc que sa formulation décrive uniquement l'environnement de q, indépendamment de la charge d'essai q0. Cela conduit naturellement à définir simplement le champ électrique par :
E→ = F→ / q0 ⇔
NB : où F→ est la force exercée sur la charge d'essai q0 ⇒ en connaissant E→ et q0, on calcule facilement F→.
E→ = kC * q * q0 / r 2 * 1r→ / q0 ⇔
E→ = kC * q / r 2 * 1r→ où [E→]=N/C.
Pour exprimer une charge négative (q ou q0) on remplace le symbole de la charge par sa définition du nombre négatif : x < 0 ⇔ x = - | x | ⇒
- si q > 0 ⇒ E→ est de même signe que 1r→ ⇒ le champ est extraverti (indépendamment du signe de la charge d'essai) ;
- si q < 0 ⇒ E→ est de signe opposé à 1r→ ⇒ le champ est intraverti (indépendamment du signe de la charge d'essai).
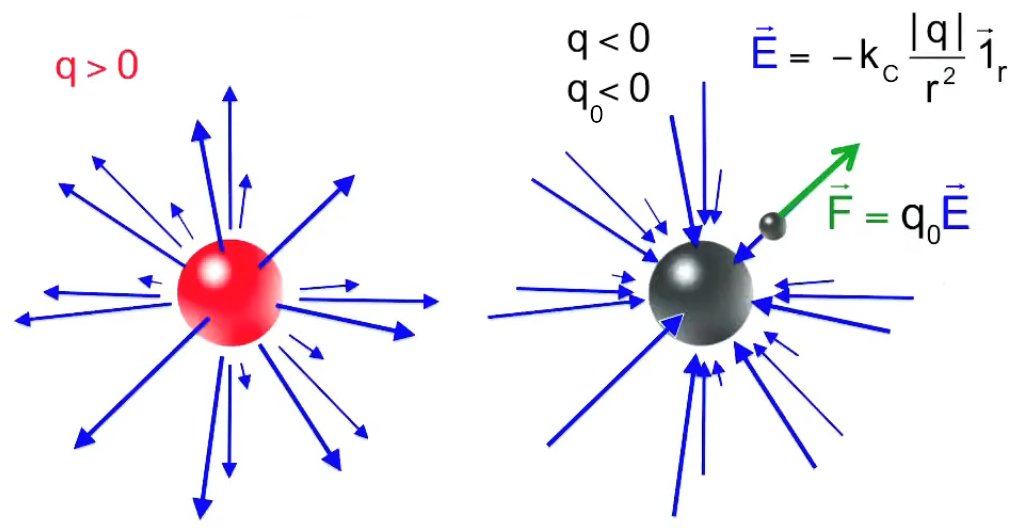
Partie droite : si la charge d'essai q0 était positive alors le vecteur vert F→ serait orienté vers q, donc dans la même direction que E→. Ainsi, alors que le champ est indépendant de la charge d'essai, la force exercée sur celle-ci ne l'est évidemment pas. Corrélativement la notion de champ ne s'intéresse pas aux forces subies par la charge q qui y est associée.
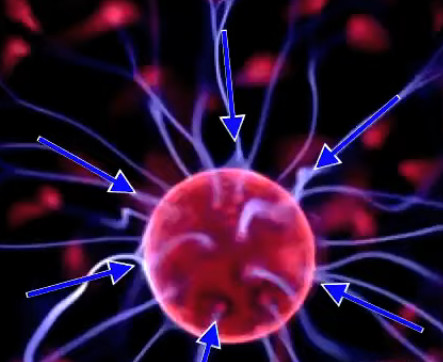
La lampe à plasma évoquée plus haut pour illustrer le phénomène de claquage est une parfaite illustration du champ électrique, dont la radialité et la tridimensionnalité. Et l'on constate qu'il correspond à la situation de droite dans l'illustration précédente.
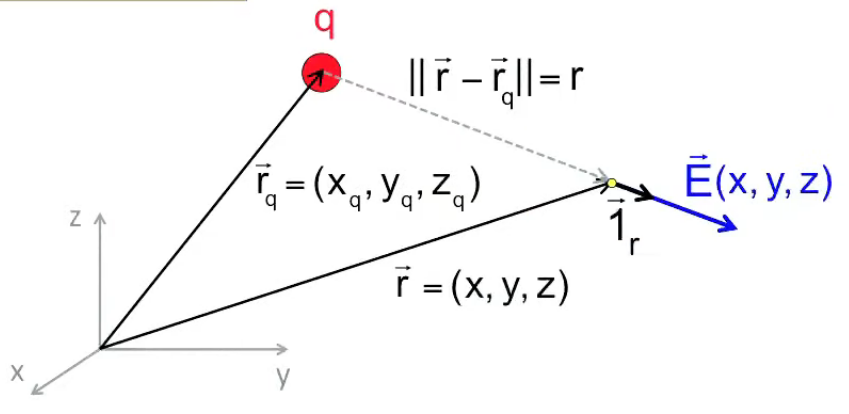
Enfin le calcul de E→ est facile puisque c'est une version simplifiée de F→, et où, par rapport au calcul applicatif de la fin de section précédente, r→2 et r→1 sont remplacés par r→ et r→q :
• r→ - r→q = ( x - xq , y - yq , z - zq )
• r = √ ( ( x - xq ) 2 + ( y - yq ) 2 + ( z - zq ) 2 )
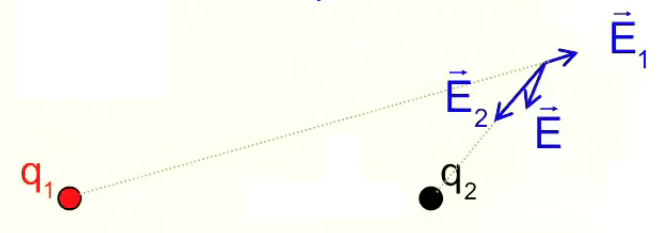
Nous venons de modéliser la notion champ électrique d’une seule charge ponctuelle (champ coulombien). Nous allons maintenant modéliser la répartition du champ électrique généré par une paire de charges électriques. Pour ce faire nous considérons la force totale engendrée par ces deux charges q1 et q2 sur une charge d’essai q0.
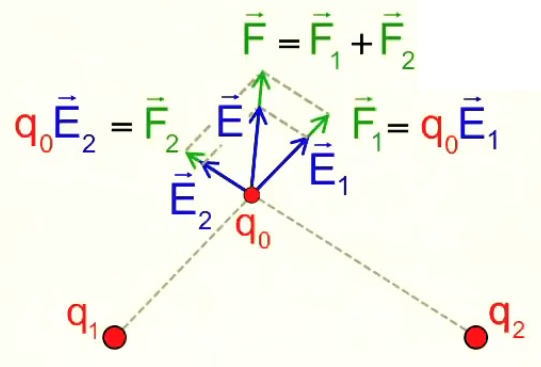
NB : le module de F→2 est plus petit, car q2 est plus éloignée de q0 (PS : les vecteurs verts sont partiellement recouverts par les bleus).
Le graphique ci-dessus montre que le principe de superposition que l'on avait constaté pour les forces électriques, vaut également pour les champ électriques : par (206) :
F→ = F→1 + F2→ = q0 * ( E1→ + E2→ ) = q0 * E→
(superposition : l'effet de q2 sur q0 n'est pas influencé par l'effet de q1 sur q0).
⇒ on retrouve :
E→ = F→ / q0
(206)
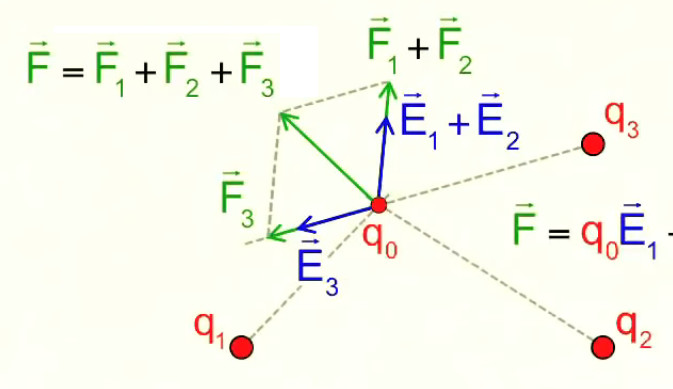
Et le principe de superposition est évidemment applicable au cas de n particules positionnées arbitrairement : E→ = ∑ nEi→
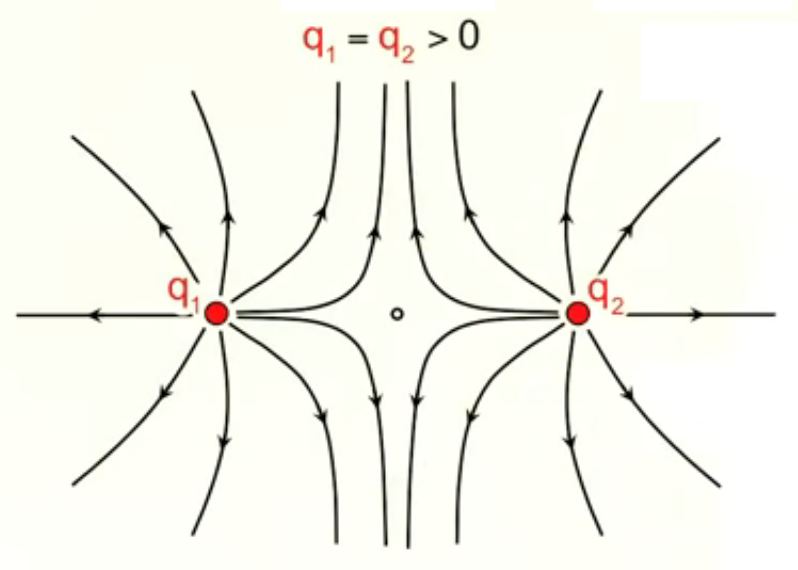
Lignes
de champ
Ainsi si l'on calcule les champs d'un nombre suffisant de charges d'essai on verra apparaître les "lignes de champ" qui caractérisent la répartition spatiale du champ. Les deux graphiques suivants montrent le cas de deux charges positives et égales. Celui de droite montre que l'élaboration complète de gauche répond aux règles simples de la superposition, ainsi que de la symétrie.
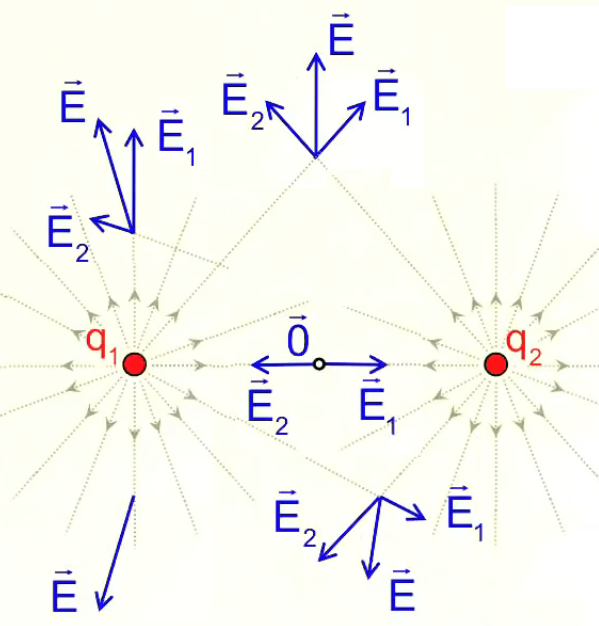
Dans le graphique suivant les deux charges sont toujours égales en valeur absolue mais de signes opposés (champ "dipolaire"). On observe encore ici les mêmes règles simples de la superposition et de la symétrie.
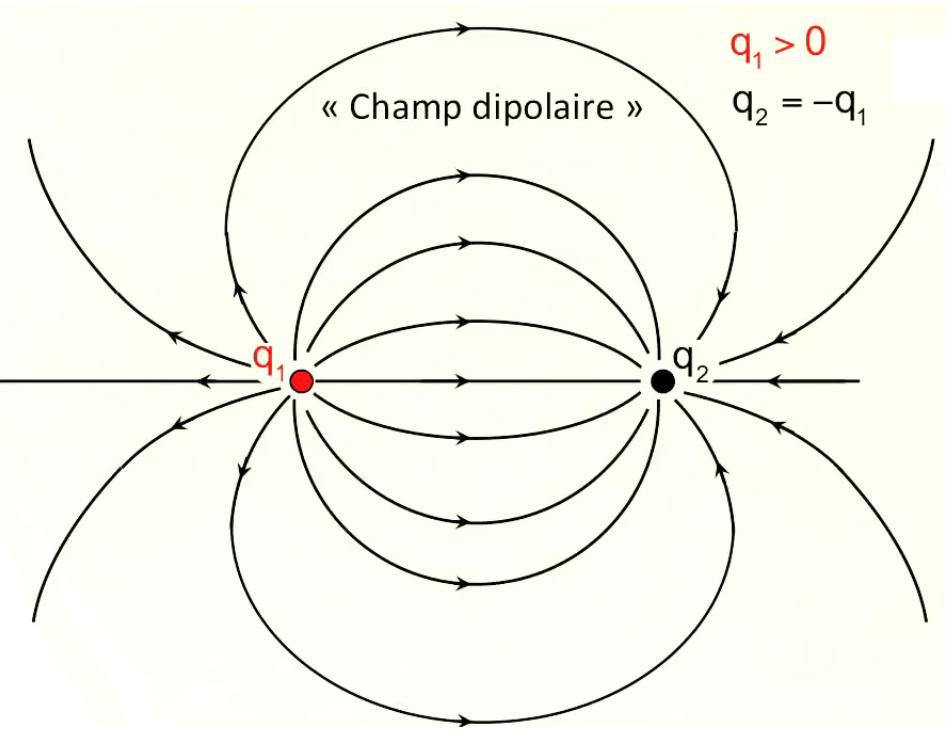
Les champs dipolaires sont fréquents, notamment à l'échelle microscopique. C'est ainsi le cas de la molécule d'eau (H2O), où les électrons ont tendance à se concentrer sur l'atome d'oxygène, et laissent donc des charges positives sur les deux atomes d'hydrogène ⇒ concentration de charges positives d'un côté, et de charges négatives de l'autre.
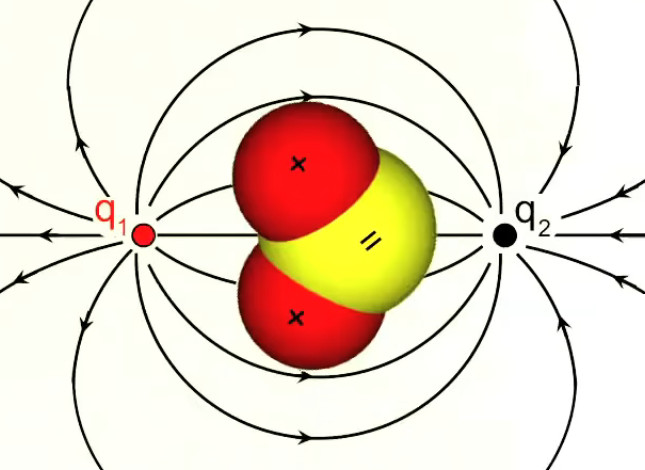
Le caractère dipolaire du champ électrique associé aux molécules de H2O explique leur état habituel sous forme liquide plutôt que gazeuse. Autre application, cette fois artificielle : dans une antenne un circuit électrique entretient un courant oscillant – c-à-d alternance de la répartition opposée des charges de signes opposés entre les deux extrémités – de sorte que celles-ci constituent un dipôle oscillant. Et c'est la nature oscillante du champ dipolaire généré par l'antenne, qui génère des ondes (dites électromagnétiques.)
Abstraction
mathématique
Dans le graphique ci-dessus considérons maintenant l'une des deux charges comme une charge d'essai (disons q2). Quel est alors la force exercée sur elle ? On pourrait être tenté de répondre à cette question en appliquant E→ = F→ / q0 (206) à q2. Mais justement : q2 n'étant pas la charge d'essai relative à un champ déterminé, il existe une infinité de E→ que l'on pourrait choisir pour calculer F→ à partir de (206) ⇒ la force exercée sur q2 est indéterminée ! Un tel calcul ne fait pas sens puisque, par définition même du champ électrique, la charge d'essai n'est pas reprise dans sa configuration. Autrement dit, on doit oublier le champ généré par la charge d'essai ⇒ il ne reste plus ici que q1 à considérer. Et comme on pourrait tenir le même raisonnement en intervertissant les rôles (q1 devenant charge d'essai) on doit en conclure que le champ électrique ne correspond à aucune réalité physique (ou, pour dire les choses plus prudemment : dans le cadre des connaissances scientifiques actuelles il est difficile de conclure que le champ électrique puisse correspondre à une réalité physique). En fait le concept de champ électrique, qui change selon la charge que l'on considère pour mesurer la force, n'est qu'un outil mathématique permettant de réaliser des calculs.
On peut enfin calculer des configuration de champs complexes, comme ci-dessous, avec même pour la configuration de droite une perte apparente de symétrie.
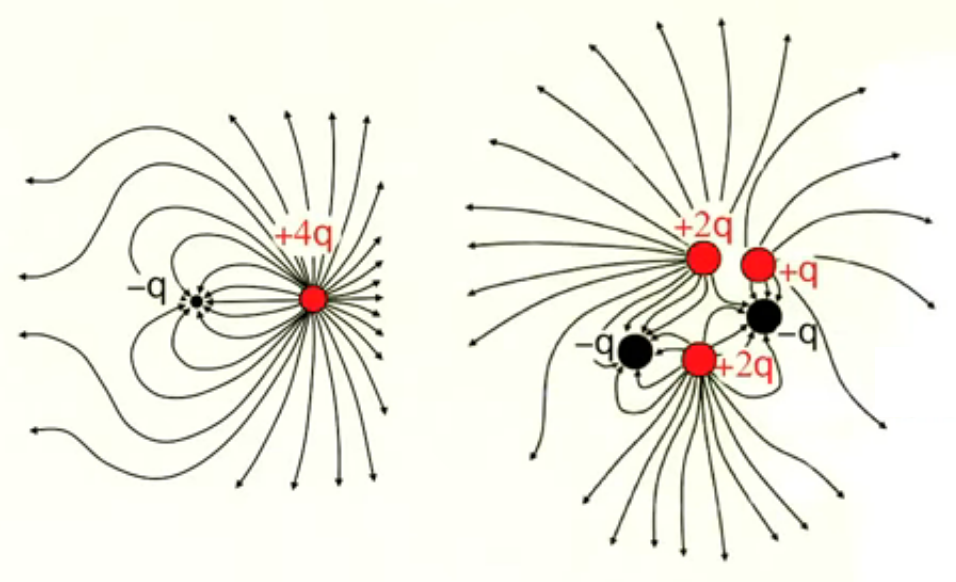
Cependant dans la pratique la notion de champ est surtout utilisée pour caractériser des composants de circuits électriques tels qu'un condensateur, qui n'est autre qu'un couple de plaques de charges opposées (cf. champ dipolaire) ce qui génère un champ entre les plaques (qui va permettre de contrôler les courants et tensions dans le circuit). On notera à cet égard que le nombre de charges sur ces plaques est tellement élevé (des milliards voire des milliards de milliards) qu'il serait fastidieux d'utiliser E→ = ∑ nEi→ (208) pour réaliser ces calculs. Dans ce type d'application on utilisera alors d'autres méthodes de calcul. Ce qui nous conduit aux chapitres suivants ...

Le condensateur d'un circuit électronique n'est autre qu'un assemblage de deux plaques constituant un champ dipolaire.
Loi de Gauss
2. Loi de Gauss : électricité
3. Distribution de charge continue
4. Forme locale et divergence
5. Théorème d'Ostrogradski
6. Méthode de Gauss : la sphère
7. Méthode de Gauss : le cylindre
8. Méthode de Gauss : le plan
Loi de Gauss : lumière
La lumière est faite de particules appelées "photons" qui avancent dans l'espace à la vitesse de 300.000 km/s. La perception continue que nous avons de la lumière est due au très grand nombre de photons qui la composent (une ampoule classique en émet des milliards de milliards par seconde).
Flux
Une source de lumière, par exemple une ampoule, est caractérisée notamment par le nombre de photons émis par unité de temps :
Φ = ΔN / Δt
(prononcer "phi")
Ce débit (ou flux), multiplié par l'énergie des photons, détermine la puissance de la source lumineuse.
Source interne. Supposons que cette ampoule est entourée d'une sphère de verre parfaitement transparente (c-à-d qu'elle laisse passer tous les photons). Soit ΦS le nombre de protons passant au travers de cette surface sphérique ⇒ Φ = ΦS (NB : Φ est le flux émis par la source, tandis que ΦS est le flux passant par la surface. On notera que cette mesure est indépendante de la taille et même de la forme de cette surface (dite "surface de Gauss") englobant la source lumineuse.
Source externe. Maintenant déplaçons cette surface de sorte qu'elle ne contient plus la source lumineuse ⇒
Φ > ΦS
et l'ont peut en outre distinguer :
• le flux sortant de ΦS, auquel par convention on attribue une valeur positive : Φs = |Φs| ;
• le flux entrant dans ΦS, auquel par convention on attribue une valeur négative : Φe = -|Φe| ;
or étant donné que par nature :
• ΦS = |Φs| - |Φe| ⇒ par convention :
ΦS = Φs + Φe
• si |Φe| > 0 ⇒ |Φs| = |Φe| ⇒ par convention :
Φs = - Φe ⇒
ΦS = Φe + Φs = 0
En résumé :
- source interne à la surface de Gauss : le flux passant par la surface est égal à celui issu de la source : ΦS = Φ
- source externe à la surface de Gauss : le flux passant par la surface est nul : ΦS = 0
Surface
ouverte
Maintenant plaçons-nous dans le cas de la source externe, et enlevons comme un couvercle la surface correspondant au flux entrant. La question qui se pose alors est de savoir ce que vaut ΦS, le nombre de photons passant au travers de cette surface ouverte.
La réponse n'est pas évidente puisque :
• la source n'étant pas interne ⇒ ΦS ≠ Φ ;
• la source n'étant pas externe ⇒ ΦS ≠ 0 ...
N.B. Quand on parle de "surface ouverte" il faut entendre "surface limitée par un contour", ce qui n'est pas le cas d'une sphère, qui est une surface fermée sur elle-même, et ne définit donc pas de contour. Le soufflage de bulles de savon illustre parfaitement cette notion de surface ouverte : si l'on ne souffle pas trop longtemps/fort dans le cercle, la "bulle" non décrochée est encore ouverte. Et si l'on arrête alors de souffler, la forme presque totalement sphérique redevient le cercle plat déterminé par le contour de l'instrument. Cette presque bulle et ce cercle plat sont deux cas de "surfaces ouvertes".

Film de savon bordé par un contour tordu
Par convention on représente cette surface "en coupe", c-à-d coupée par un plan perpendiculaire à l'axe de vision ⇒ on obtient une ligne quelconque (une droite dans le cas du cercle plat orienté non parallèlement au plan).
Densité
de flux
Supposons maintenant une source lumineuse émettant un faisceau parallèle. L'image ci-dessous représente un volume ΔV contenant ΔN photons, passant à vitesse v au travers de la surface S pendant une durée Δt. D'autre part on suppose que la densité volumique des photons η = ΔN / ΔV est connue.
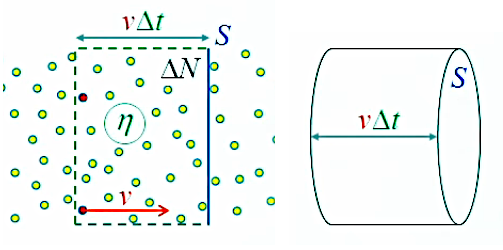
On a donc que :
• ΔV = v * Δt * S (par (162) )
• ΔN = η * ΔV
⇒
ΔN = η * v * Δt * S
or par définition :
ΦS = ΔN / Δt ⇒
ΦS = η * v * S
Ce résultat intuitif montre donc que l'intensité du flux sur une surface S est déterminée par le produit densité*vitesse, que l'on appelle la "densité de flux" :
F = η * v ⇒
ΦS = F * S
⇔
F = ΦS / S
La densité de flux mesure donc le flux par unité de surface. C'est la mesure de l'intensité de la lumière émise par la source.
On va maintenant généraliser au cas d'une surface inclinée d'un angle θ (par rapport à la perpendiculaire au champ de photons). En outre cette surface est de forme carrée telle que S=L2.
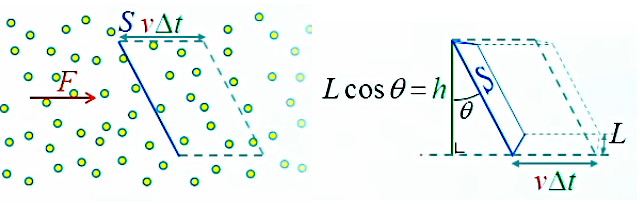
Le volume de Gauss devient donc :
ΔV = v * Δt * L * h ⇔
ΔV = v * Δt * L * L * cosθ ⇔
ΔV = v * Δt * S * cosθ ⇒
ΔN = η * ΔV = η * v * Δt * S * cosθ ⇒
ΦS = ΔN /Δt = η * v * S * cosθ ⇔
ΦS = F * S * cosθ
Ainsi en comparant (211) et (212), cosθ (dont la valeur absolue est ≤ 1) apparaît comme un facteur de réduction de la surface suite à son inclinaison. En fait il s'agit de la réduction de la surface "de prise au flux". Ainsi si θ=π/2, plus aucun photon ne traverse la surface, et cos(θ)=0.
Alternativement, en associant cosθ à v (ΦS = η * v * S * cosθ), on peut le voir aussi comme un facteur de réduction de la vitesse, car seule la composante normale (perpendiculaire à la surface) de la vitesse intervient dans le calcul du flux.
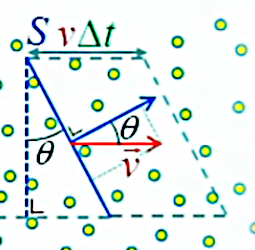
Cette remarque nous conduit naturellement à introduire la notation vectorielle : F→ = η * v→ de sorte que F→ caractérise le flux non seulement dans son intensité mais aussi sa direction.
F→ représente donc le champ vectoriel des photons.
Vecteur de
surface
Nous pouvons maintenant introduire une notion fondamentale de la loi de Gauss : le vecteur de surface S→, normal à la surface (c-à-d perpendiculaire à celle-ci), et dont le module est cette même surface. Ce vecteur va permettre d'exprimer également l'orientation de la surface.
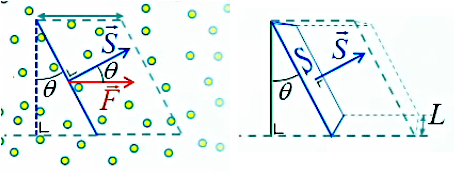
On arrive à cette notion de vecteur de surface en considérant que puisque θ est l'angle séparant F→ et S→ (tous deux sont perpendiculaires aux axes formant θ) on peut donc considérer ΦS = F * S * cosθ comme un produit scalaire (58) :
ΦS = F→ . S→
où S→ est appelé "vecteur de surface".
S * cos(θ) est donc la projection du module S sur la direction du flux F→.
Surface quelconque. Étendons la généralisation en considérant maintenant une surface ouverte de forme quelconque. Ensuite découpons-là en damier de petites surfaces carrées telle que :
S = ∑n=1N ΔSn
Comme ces carrés peuvent être arbitrairement petits on peut alors approcher idéalement la surface ouverte quelconque. Chacun de ces petits carrés peut être représenté par son vecteur de surface, de sorte que leur somme est aussi vectorielle : S→ = ∑n=1N ΔS→n
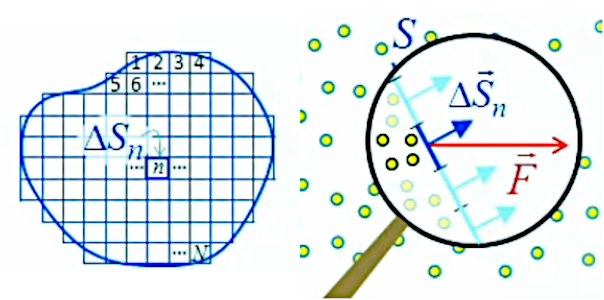
⇒ on peut alors décrire le flux passant par chacun de ces petits carrés :
ΦΔSn = F→ . ΔS→n ⇒
ΦS = ∑n=1NΦΔSn = ∑n=1N F→ . ΔS→n ⇔
ΦS = F→ . ∑n=1N ΔS→n = F→ . S→
On retrouve donc le même résultat que celui obtenu avec la surface carrée, de sorte que l'on peut faire le même type d'interprétation de cos(θ) : soit comme facteur de réduction de la surface suite à son inclinaison, soit comme facteur de réduction de F→ via la vitesse.
Champ non uniforme. Continuons la généralisation en considérant maintenant un champ non uniforme : la source émet maintenant dans toutes les directions, de sorte que F→ est variable sur la surface, ce que l'on va exprimer en le notant F→n. Mais alors la dernière égalité n'est plus valable car F→n ne peut plus être extrait de la somme puisqu'il dépend de n (et n'est donc plus constant) :
ΦS = ∑n=1NΦΔSn = ∑n=1N F→n . ΔS→n
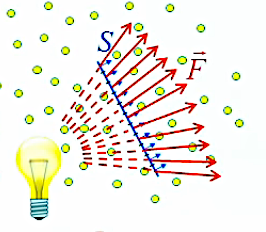
Si l'on perd en simplicité on gagne cependant en généralité car maintenant on va pouvoir supposer n'importe que forme pour la surface de Gauss ! Pour cela on va passer à la limite infinitésimale :
ΔS→n → dS→n ⇒
ΦS = ∫s F→ . dS→
NB : les indices n doivent être enlevés car ces dS sont en nombre infini, donc non énumérables.
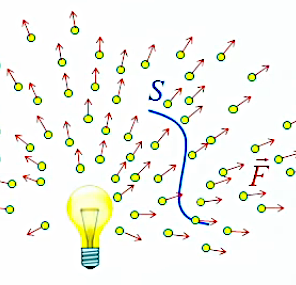
Notons que la formulation supra est minimaliste : sa notation complète (mais rare) est plutôt : ΦS = ∫s F→(r→) . dS→(r→). C'est en effet le vecteur position r→ qui détermine un point particulier sur la surface de Gauss, auquel correspond un vecteur de surface dS→(r→) d'inclinaison particulière par rapport au champ F→(r→).
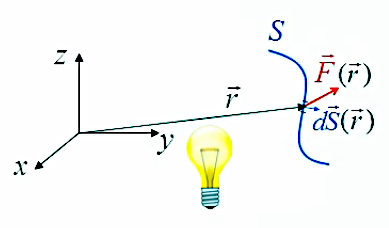
Surface quelconque fermée. La surface de Gauss est fermée par définition. On le formule au moyen d'une notation spéciale de l'intégrale, dont le signe est maintenant affublé d'un petit cercle : ΦS = ∮s F→ . dS→ = Φ
Rappel : le flux émis par la source (Φ) est égal à celui passant par la surface (ΦS) dès lors que celle-ci englobe la source (210).
Par convention les physiciens ont choisi que les vecteurs de surface d'une surface fermée sont sortants, que la source soit interne ou externe.
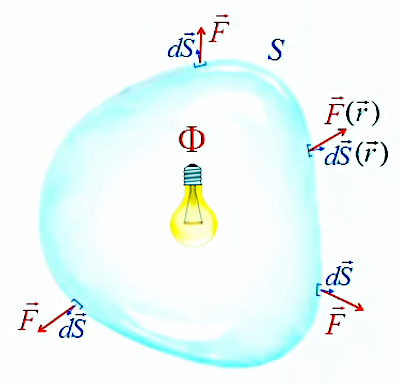
Il en résulte qu'un flux sortant d'une surface fermée est toujours positif : car on a alors θ<π/2 ⇒ cos(θ)>0. En effet θ<π/2 puisque d'une part dS→ est perpendiculaire à la surface, et que d'autre part F→ ne peut former un angle supérieur à π par rapport à celle-ci, qui entoure la source.
N.d.A. Cette convention est la corollaire de la double convention Φe = -|Φe| et Φs = |Φs| ayant conduit à ΦS = Φe + Φs = 0 (210).
Le graphique ci-dessous illustre le cas d'une source externe. Les produits scalaires (213) correspondant à la calote d'entrée (Φe) sont négatifs car leur θ>π/2 ⇒ leur cos(θ)<0. La limite de cette calotte correspond au passage des cos(θ) de valeurs négatives à positives c-à-d au passage de θ>π/2 à θ<π/2 de sorte que ce point de passage est tel que θ=π/2 c-à-d la perpendicularité entre les deux vecteurs F→ (tangent à la surface, et sortant de celle-ci) et dS→.
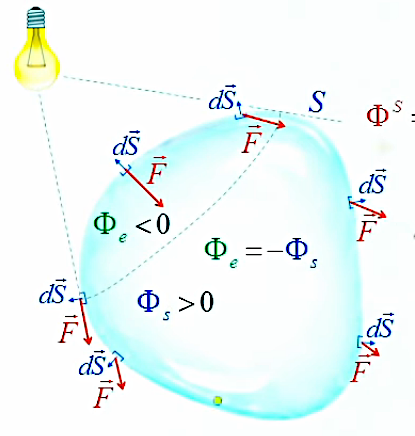
N.B. Étant donné la forme quelconque de la surface fermée, si le nombre de photons est très faible on pourra avoir des mesures sur des dt telles que |Φe| ≠ |Φs|. Cependant l'égalité Φe = - Φs est bien vérifiée en moyenne sur une certaine période.
Nous somme maintenant en mesure d'exprimer la loi de Gauss pour la lumière. Pour ce faire on va d'abord considérer deux sources à l'intérieur de la surface fermée.
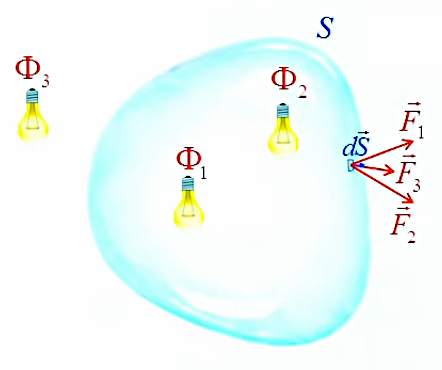
À un vecteur de surface dS→ sont donc associés deux vecteurs F→1 et F→2 tels que :
ΦS = ∮s ( F→1 + F→2 ) . dS→ ⇔
ΦS = ∮s F→1 . dS→ + ∮s F→2 . dS→ ⇔
ΦS = Φ1 + Φ2
Ce résultat est inchangé si l'on ajoute une source cette fois extérieure, et dont le flux est donc nul (210). Par conséquent la loi de Gauss peut être formulée généralement par :
ΦS = ∮s F→ . dS→ = ∑ Φint
où n'interviennent donc que les flux de sources internes à la surface de Gauss.
Considérons maintenant le cas d'une source lumineuse ponctuelle (que l'on peut voir comme une sphère de rayon infiniment petit) dont le débit de photons est Φ. Étant donnés ΦS=Φ (c-à-d connus) on veut calculer en tout point la valeur du champ vectoriel F→( r→).
Dans une première étape on considère que ΦS est une sphère de rayon r, et que Φ se situe en son centre. Dans ce cas les vecteurs de surface sont parallèles à leur densité de flux F→ (211) c-à-d que θ=0 ⇔ cos(θ)=1 ⇒
ΦS = ∮ F(r) * dS
NB : ce n'est plus un produit scalaire : "*" a remplacé "."
et en outre les F(r) sont constants en raison de la symétrie du système ⇒
ΦS = F(r) * ∮ dS ⇔
ΦS = F(r) * S ⇔ par (108) :
ΦS = F(r) * 4 * π * r2
or
ΦS = Φ ⇒
F(r) = Φ / ( 4 * π * r2 ) ⇒
F→( r→) = Φ / ( 4 * π * r2 ) * 1→r
On exprime ainsi l'intensité lumineuse en fonction de la distance à la source. Et en particulier il apparaît que la densité de flux de photons est une " fonction vectorielle radiale (cf. 1→r) en 1/r2 ".
Application. Le rapport entre l'intensité lumineuse à la surface du soleil et celle de la Terre vaut :
Φ / ( 4 * π * RS2 ) / ( Φ / ( 4 * π * RT2 ) ) = RT2 / RS2 = 150.000.000 / 700.000 ≈ 46.000
⇔ le rayonnement du soleil est donc environ cinquante mille fois plus élevé au niveau du soleil qu'à celui de la terre.
Cette configuration sphérique, pas sa symétrie, a considérablement facilité le développement aboutissant à (215) en rendant possible l'extraction de F(r) hors de l'intégrale, puisque dans cette configuration r est constant, et donc F(r) également par (202). Mais dans le cas d'un espace fermé ΦS de forme quelconque, ce n'est plus le cas, car r varie selon le vecteur de surface, et donc F(r). Dans cette situation, l'utilisation de (214) serait fastidieuse car le calcul intégral serait gigantesque. C'est là qu'intervient le théorème de Gauss, qui va démontrer que (215) demeure la solution de (214) même en cas de surface gaussienne quelconque !

Théorème
de Gauss
Pour ce faire la démonstration du théorème de Gauss décompose la sphère originelle en tubes de flux, tels que le flux de protons émis par le centre de la sphère ne passe que par l'entrée et la sortie des tubes, mais pas par leur parois, de sorte que le flux de protons Φ qui sort de l'ensemble de ces tubes est égal à celui qui y entre !
La première étape du développement du théorème de Gauss consiste à décomposer la surface de la sphère en un nombre N de sections hexagonales, dont la surface unitaire ΔS vaut donc ΔS = 4 * π * r2 / N. À chacune de ces ΔS correspond donc un flux Φ/N.
On peut alors considérer des tubes de flux de longueurs différentes, ainsi que des tailles arbitrairement petites pour les sections de surface ΔS (qui deviennent des dS, avec un N arbitrairement élevé) ⇒ la surface fermée entourant la sphère avec les tubes de flux peut être de forme quelconque.
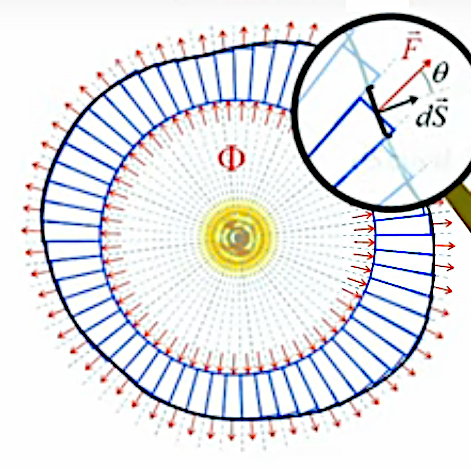
Coupe transversale d'une sphère recouverte de tubes de flux de longueur variable. .
D'autre part la loupe illustre le fait que le flux ΦS/N passant au travers de la surface noir est le même que celui passant au travers de la section d'un tube de flux (en bleu) (213). Par conséquent le flux ΦS qui passe au travers de la surface quelconque entourant la sphère avec les tubes de flux est égal à celui qui passe par l'ensemble des tubes, qui est lui-même celui passant par la sphère, soit Φ ⇔ ΦS = Φ où ΦS est une surface fermée de forme quelconque entourant la sphère dont le centre est la source de Φ.
N.d.A. La loupe montre également que l'on peut arbitrairement approcher la propriété de départ du cas symétrique de la sphère, à savoir que les vecteurs de surface sont parallèles à leur densite de flux F→ (211) c-à-d que : θ=0 ⇔ cos(θ)=1 ⇒
ΦS = ∮ F(r) * dS
où ΦS est quelconque (et donc r variable)
or soit :
dS = 4 * π r2 / N ⇒
ΦS = ∮ F(r) * 4 * π r2 / N ⇒
si (215) est vrai pour ΦS quelconque ⇒
ΦS = ∮ Φ / N ⇔
ΦS = Φ
ce qui est vrai ⇒ (215) est donc vrai pour ΦS quelconque.
On a ainsi démontré le théorème de Gauss :
F→( r→) = Φ / ( 4 * π * r2 ) * 1→r ⇔
ΦS = ∮s F→ . dS→ = Φ
qui, en démontrant la validité de la transformation de la relation "⇐" en "⇔", facilite grandement l'utilisation de ΦS = ∮s F→ . dS→ = Φ dans les cas où S représente une surface quelconque.
Le théorème de Gauss est accompagné d'un complément qui concerne le cas d'une source externe à une surface fermée, laquelle est analysée comme un agrégat de tubes de flux. Or nous avons vu que dans le cas d'une source externe ΦS est nul (210).
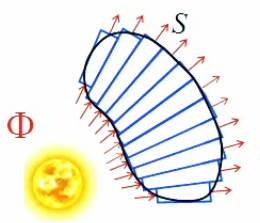
Coupe transversale d'une sphère recouverte de tubes de flux de longueur variable.
Ce type de champ est appelé "à divergence nulle", concept intimement lié à la loi de Gauss, et qui traduit le fait que les photons traversent la sphère sans s'accumuler en son sein (ils la traverse à vitesse constante). C'est ainsi également le cas d'un champ électrique ou gravitationnel dans le vide.
Loi de Gauss : électricité
Tous les phénomènes électro-magnétiques peuvent être décrits par le système d'équations de Maxwell (qui sort du cadre de ce cours) :
- ∇ * B = 0
exprime la conservation du flux magnétique (210) ; -
∇ * E = ρ / ε0
exprime la distribution de charge continue de la loi de Gauss (224); - ∇ x E = - δB / δt
exprime, avec l'équation suivante, le couplage (effet de boucle) entre champs électrique (E) et magnétique (B). - ∇ x B = μ0 * J + μ0 * ε0 * δE / δt
Le champ magnétique est plus souvent caractérisé par la densité de flux magnétique ou induction magnétique B→ exprimée en Teslas (T), que par son intensité H→, ces deux grandeurs étant liées par la relation B→ = μ * H→ où μ représente la perméabilité magnétique du milieu.
Dans la présente section et la suivante nous allons montrer que la seconde équation correspond effectivement à la loi de Gauss, sous forme différentielle (alors que dans la section précédente on l'a développée sous forme intégrale).
Repartons du théorème de Gauss :
F→( r→) = Φ / ( 4 * π * r2 ) * 1→r ⇔
ΦS = ∮s F→ . dS→ = Φ (216)
L'égalité de gauche correspond à certains phénomènes physiques, qui peuvent être modélisés mathématiquement sous forme de fonction radiale en 1/r2 par rapport à un point déterminé de l'espace. C'est le cas du champ électrique.
En fait il y a généralisation lorsque l'on passe de Coulomb (électricité) à Gauss (lumière) :
- électricité : champ de Coulomb : champ électrique dû à une charge ponctuelle E→ = kC * q / r 2 * 1r→ (207).
- lumière : champ de Gauss : champ de "densité de flux" de particules, émises par une source ponctuelle de débit Φ F→ = Φ / ( 4 * π * r2 ) * 1→r (215) et
N.d.A. : ne pas confondre le F de Coulomb, qui est la force électrique, et le F de Gauss, qui est le champ. Autrement dit : le champ de Coulomb E correspond au chams de Gauss F (densité de flux).
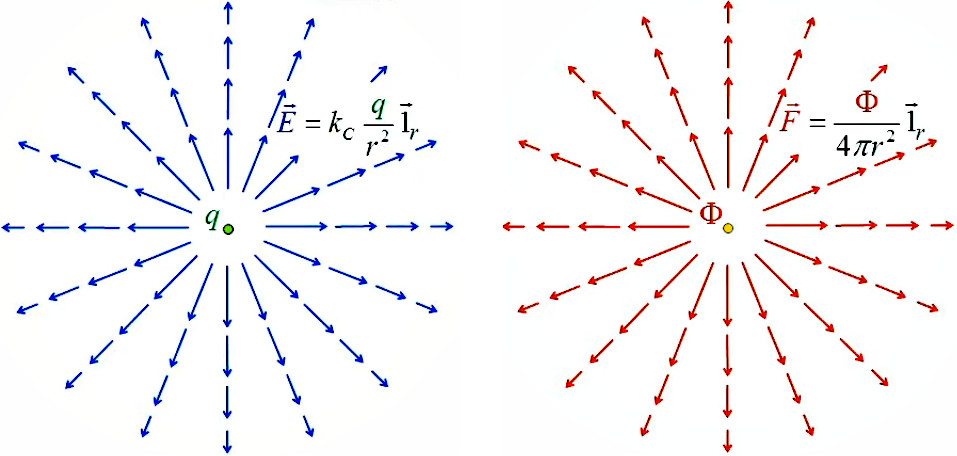
Pour formaliser l'analogie entre ces deux équations il suffit de créer une variable
Φq = 4 * π kC * q
de sorte que (207) devient :
E→ = Φq / ( 4 * π * r 2 ) * 1r→
qui ne diffère de (215) que par le remplacement de Φ par Φq (où l'indice q signifie qu'il s'agit d'une constante qui est proportionnelle à la charge électrique qui génère le champ).
Le champ électrique peut donc être vu aussi comme une densité de flux de particules, à tel point que les charges électriques sont parfois appelées "photons virtuels" (cf. théorie quantique des champs). On en déduit ainsi que le champ électrique obéit également à la loi de Gauss : ΦES = ∮s E→ . dS→ = Φq où ΦES est donc le flux du champ électrique sur la surface fermée S. En particulier si la source est externe, alors le flux électrique net est nul par rapport à la surface fermée S.
Soulignons ici toute la puissance du théorème de Gauss (216) : en substituant l'égalité de gauche dans celle de droite, on obtient une intégrale :
ΦES = ∮s Φq / ( 4 * π * r 2 ) * 1→r . dS→
⇒ par (58) :
ΦES = ∮s Φq / ( 4 * π * r 2 ) * cos(θ) * dS
où θ est l'angle entre le vecteur de surface (perpendiculaire à la surface par définition) et l'axe passant pas la source et l'origine du vecteur de surface ⇒ comme la surface globale est quelconque (non symétrique) ⇒ θ≠0 ⇔ cosθ≠1, et r et θ varient selon le ds. Il en résulte que le calcul de cette intégrale requiert un ordinateur ... mais le théorème de Gauss nous dit précisément que, même pour une surface quelconque, la solution est tout simplement Φq !
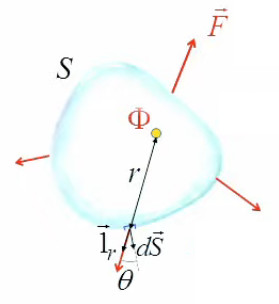
La notion de débit de photons virtuel étant abstraite, on note ΦES en fonction de q plutôt que de Φq :
ΦES = ∮s E→ . dS→ = Φq
devient, par (217) :
ΦES = ∮s E→ . dS→ = 4 * π kC * q
Permittivité
Cette version de la loi de Gauss fut en outre simplifiée par le chercheur autodidacte Oliver Heaviside, qui introduisit la notion de permittivité du vide :
ε0 = 1 / ( 4 * π * kC ) = 8,85*1012 C2/(N*m2)
, analogie avec la permittivité de l'air, qui est une propriété d'élasticité permettant d'expliquer la propagation des ondes acoustiques dans l'air ⇒
ΦES = ∮s E→ . dS→ = q / ε0
qui est la version moderne de la loi de Gauss pour le champ électrique.
De la même manière la forme moderne de la loi de Coulomb exprime le champ électrique en fonction de la permittivité ε0 plutôt qu'en fonction de la constante de Coulomb kC, de sorte que :
E→ = kC * q / r 2 * 1r→ (207) devient :
E→ = q / ( 4 * π * ε0 * r 2 ) * 1r→ .
Électrodynamique
L'équivalence entre les lois de Coulomb et de Gauss ne concerne cependant que les phénomènes électrostatiques, c-à-d lorsque la charge à la source du champ est statique. Mais lorsque l'on considère que les charges ne sont pas fixes (ce qui est généralement le cas dans le monde physique), on doit prendre en compte le fait que cette dynamique ne se propage pas instantanément sur le champ (temps de propagation des photons virtuels). Or ce retard a pour effet de supprimer la propriété de radialité : le champ n'est plus dans l'axe situé entre la charge et le point de calcul. Il en résulte que la loi de Coulomb n'est plus valable. Par contre la loi de Gauss demeure valable dans le cas de charges non statiques.
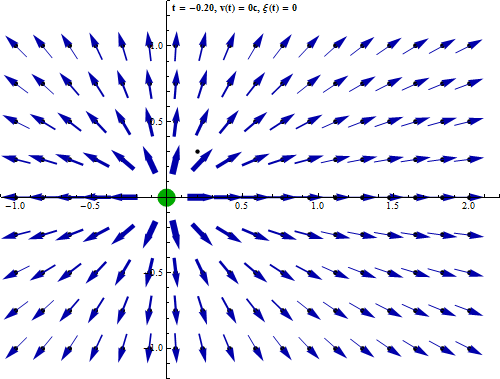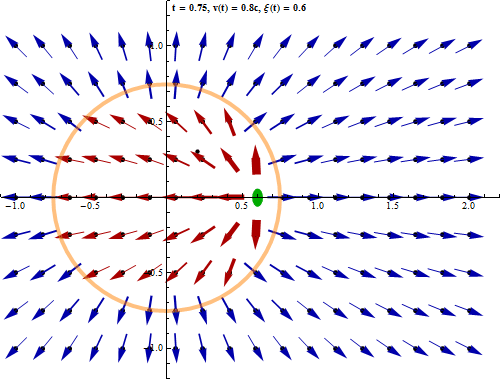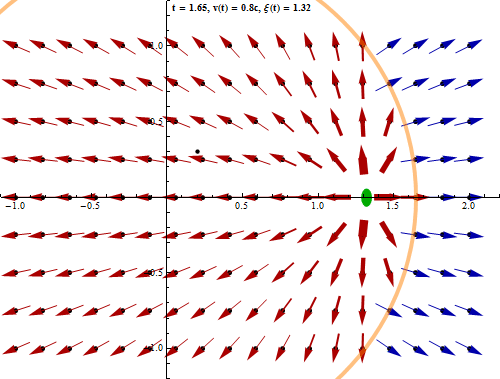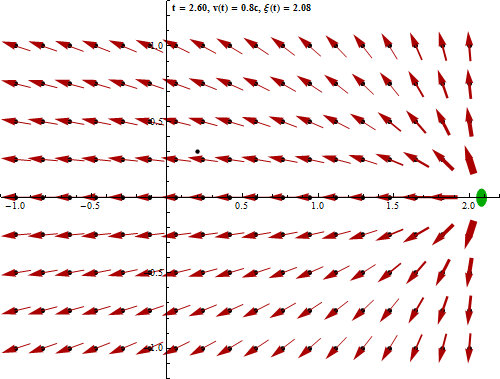
Cette animation montre que lorsqu'un corps chargé se déplace, le champ électromagnétique qu'il génère n'est pas déplacé en bloc mais de proche en proche [source].
Charges
négatives
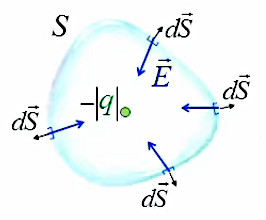
Dans le cas du champ E→ généré par une charge négative -|q|, celui-ci est orienté vers la charge (cf. #champ-electrique). Et comme d'autre part les vecteurs de surface d'une surface fermée sont sortants par convention (cf. supra #vecteur-surface) ⇒
θ > π / 2 ⇒ cosθ < 0 ⇒ par (58) :
ΦES = ∮s E→ . dS→ < 0
On le démontre trivialement en remplaçant q par -|q| dans ∮s E→ . dS→ = q / ε0 (219). La loi de Gauss vaut donc également pour les charges négatives.
Charges
multiples
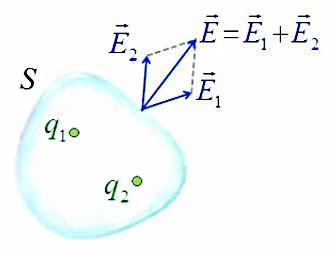
La loi de Gauss devient :
∮s E→ . dS→ = ∑n qn / ε0
dont la démonstration est triviale :
ΦES = ∮s E→ . dS→ =
∮s ( ∑n E→n ) . dS→ =
∑n ∮s E→n . dS→ =
∑n qn / ε0
CQFD
Charges
externes
Enfin la prise en compte de charges externes est également triviale. Le graphique suivant illustre le fait que le champ généré par les charges externes modifie le champ généré par les charges internes.
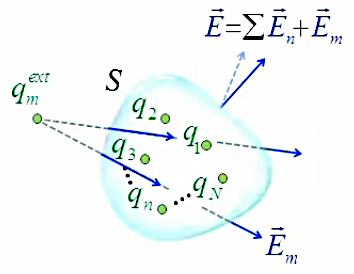
Enfin la prise en compte de charges externes est également triviale. Le graphique suivant illustre le fait que le champ généré par les charges externes modifie le champ généré par les charges internes. On montre que le résultat est cependant sans effet, en prenant le cas d'une charge externe qm :
ΦES = ∮s E→ . dS→ =
∮s ( ∑n E→n + E→m ) . dS→ =
∑n ∮s E→n . dS→ + ∮s E→m . dS→ =
par (210) :
∑n ∮s E→n . dS→ =
∑n qn / ε0
CQFD
Autrement dit, seules interviennent les charges internes dans la loi de Gauss, que l'on peut donc énoncer comme suit : « l'intégrale de flux d'un champ électrique sur une surface fermée est donnée par la somme des charges que contient cette surface, divisée par la permittivité du vide ».
Distribution de charge continue
Nous allons ici généraliser la loi de Gauss pour les distributions de charges continues. Cette notion est illustrée par une expérience d'électrostatique consistant à accumuler des charges de signes oppposés dans deux boules, jusqu'à ce qu'un certain seuil soit dépassé, provoquant un "claquage" : l'air s'ionise et créé ainsi le passage d'un courant d'une boule vers l'autre, ce que l'on observe sous la forme d'un arc électrique. On va étudier ici ce qui se passe dans ces boules avant le claquage : dans chaque boule la charge est statique de sorte que l'on peut appliquer la loi de Gauss.
À l'échelle microscopique les ions (+) du réseau cristallin constituant la matière métallique de la boule sont entourés d'électrons (-) en agitation thermique. Les ions sont également en agitation thermique mais beaucoup plus faible, de sorte qu'on peut les considérer comme relativement immobiles : il bougent autour d'une position d'équilibre, tandis que les électrons forment un nuage réparti dans l'ensemble du volume de la boule. Le mouvement des électrons n'est pas ordonné tant qu'il n'y a pas de courant. Mais en moyenne, dans le volume déterminé par la boule, on peut considérer que la position des charges est constante. Pour que cette condition soit vérifiée il suffit que le nombre de charges soit constant en moyenne. On est alors dans les conditions de la loi de Gauss : ensemble discret de charges statiques.
Formellement on doit préciser que seules les charges internes sont prises en considération :
∮s E→ . dS→ = ∑nint qn / ε0
Cependant la réalité est dynamique plutôt que statique. Pour adapter le modèle à cette dynamique il faut introduire la notion de distribution de charges continue. Il s'agit de partitionner l'espace en petits cubes de volumes identiques ΔV, et dans lesquels les conditions de l'électrostatique (ensemble discret de charges statiques ⇔ ∄ courant) sont vérifiées en moyenne (notamment les sorties d'électrons hors de chaque cube sont compensées en moyenne par des entrées).
Ainsi à chaque ΔV est associée une quantité de charges (ions + électrons) ΔQ = ∑n qn. Chacun des cubes est considéré comme chargé c-à-d de charge totale non nulle : #charges+ ≠ #charges-.
Densité
volumique
On introduit alors la notion de densité volumique de charge :
ρ = ΔQ / ΔV [C/m3] .
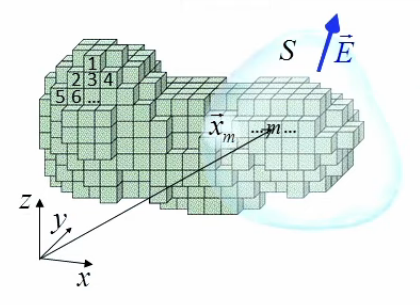
Pour exprimer le fait que ρ varie d'un cube à l'autre (et donc aussi ΔQ puisque ΔV est identique pour tous les cubes) on va identifier chacun de ceux-ci au moyen d'un vecteur position : x→m = ( xm , ym , zm )
⇒
ρ(x→m) = ΔQm / ΔV ⇔
ΔQm = ρ(x→m) * ΔV ⇒
dans (222) on remplace alors le terme qn (représentant les charges élémentaires) par ΔQm (représentant la charge contenue par chaque cube) :
∮s E→ . dS→ = 1/ε0 * ∑mint ΔQm ⇔ par (223) :
où ∑mintΔQm est la somme des charges contenues par les seuls volumes ΔV contenus dans l'espace déterminé par la surface fermée S
∮s E→ . dS→ = 1/ε0 * ∑mint ρ(x→m) * ΔV
qui est une somme discrète ⇒ pour passer à la distribution de charge continue on va considérer que ΔV → 0 ⇔ ΔV = dV ⇒
• la variable discrète x→m devient une variable continue x→ ;
• la somme discrète ∑mint devient une intégrale ∫VS, calculée sur le domaine du volume V enfermé par la surface S :
∮s E→ . dS→ = 1/ε0 * ∫vs ρ(x→) * dV
où :
• ε0 est la permittivité du vide (218)
• ρ est la densité volumique de charge (223)
Lecture : le membre de gauche est l'intégrale d'un flux E→ sur une surface fermée ( ∮s ), tandis que le membre de droitre est l'intégrale d'une densité de charge ρ(x→) dans un volume ( ∫vs ), ce volume étant celui contenu dans la surface fermée.
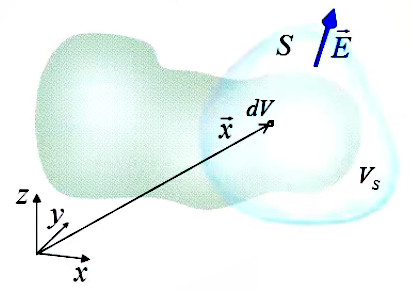
NB : les points situés entre la surface de Gauss (S) et la surface de l'objet de volume VS, c-à-d là où il n'y a pas de charge, sont tels que ρ(x→m) = 0.
Forme locale et divergence
La forme continue de la loi de Gauss ∮s E→ . dS→ = 1/ε0 * ∫VS ρ(x→) * dV (224) n'est pas locale : elle met en relation des points de la surface fermée (membre de gauche) avec des points à l'intérieur de cette surface fermée (membre de droite).
Rappelons que, par ΦES = ∮s E→ . dS→ = q / ε0 (219), l'intégrale du membre de droite de l'égalité ci-dessus représente la charge électrique enfermée dans VS (le volume V circonscrit par la surface S).
Nous allons ici développer la version locale de la loi de Gauss : div(E→) = ρ(x→) / ε0
qui met en relation E→ et ρ(x→) en un même point (déterminé par le vecteur position x→), et implique la notion de divergence.
Pour passer de la version continue (224) à la version locale (229) on considère une surface fermée de forme cubique, que l'on réduit à un volume infinitésimal entourant un seul point.
Pour ce faire nous allons devoir faire ici une parenthèse sur le traitement des intégrales calculées sur de très petits intervalles. Commençons à une dimension (c-à-d une seule variable).
Le graphique ci-dessous illustre le fait que lorsque l'intervalle δ tend vers zéro, le segment de la courbe f(x) qu'il détermine peut être considéré comme une droite. Dans ces conditions, le point situé au milieu de cet intervalle détermine deux triangles identiques :
• en vert au-dessus de la ligne horizontale hachurée, dans la partie droite de l'intervalle ;
• en blanc en-dessous de la ligne horizontale hachurée, dans la partie gauche de l'intervalle.
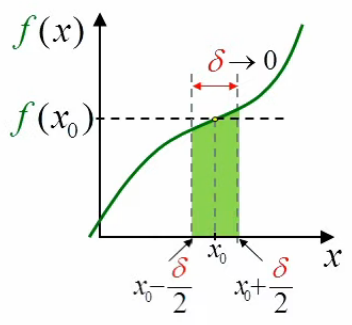
On voit alors que la valeur de l'intégrale limδ→0 ∫x0–δ/2x0+δ/2 f(x) * dx (la surface en-dessous de la courbe) est égale à la surface du rectangle δ * f(x0).
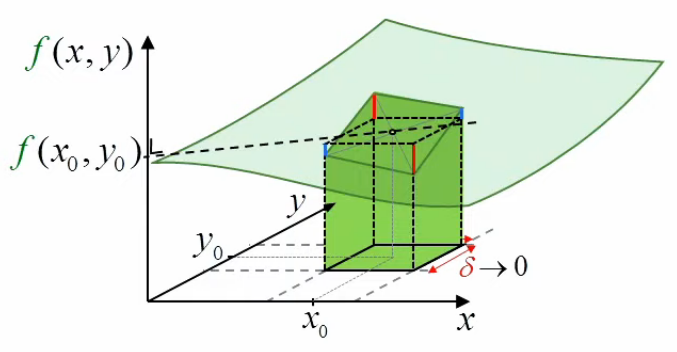
Ce résultat se généralise facilement au cas de deux dimensions : dans le graphique ci-dessus x0, point central de la base du rectangle dont la surface représente l'intégrale, devient dans le graphique suivant (x0,y0), point central de la base d'un parallélépipède rectangle dont le volume (membre de droite suivant) représente l'intégrale (membre de gauche suivant) : limS→0 ∫S f(x,y) * dS = δ2 * f(x0,y0)
où dS=dx*dy
∮s E→ . dS→ = 1/ε0 * ∫VS ρ(x→) * dV : forme continue de la loi de Gauss ;
à :
div(E→) = ρ(x→) / ε0 : forme locale de la loi de Gauss.
La première partie de cette démonstration concerne le membre de droite de la forme continue : si l'espace fermé de forme cubique est réduit à un point (déterminé par le vecteur) x→, alors ρ(x→0) peut être sorti de l'intégrale :
limvS→0 ∮s E→ . dS→ = limvS→0 1/ε0 * ρ(x→) * ∫VS dV ⇔
limvS→0 ∮s E→ . dS→ = limvS→0 1/ε0 * ρ(x→) * VS ⇔
limvS→0 ∮s E→ . dS→ = 1/ε0 * ρ(x→0) * δ 3
La seconde partie de la démonstration, plus longue et calculatoire, concerne le membre de gauche de la forme continue. S'agissant d'une intégrale de flux nous allons donc calculer ce flux sur toutes les surfaces du cube.
Commençons par celle du haut. Nous la dénommons Sz car orientée en z :
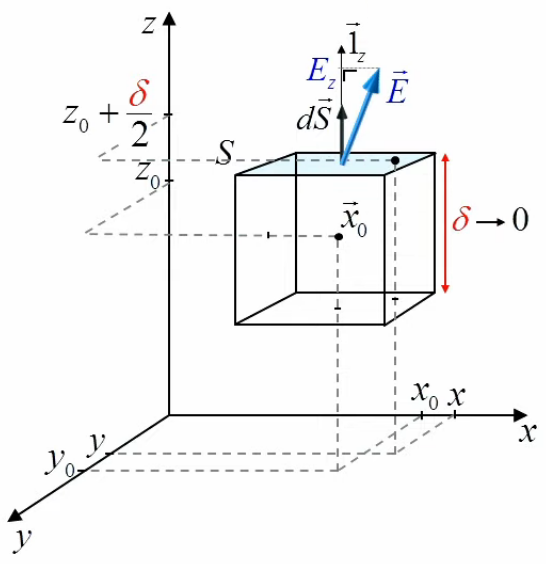
NB : le dS→ ne représente pas cette surface, mais une surface infinitésimale telle que :
dS→ = dS * 1→z ⇒
∮sz E→ . dS→ =
∮sz E→ . dS * 1→z =
∮sz E→ . 1→z * dS =
∮sz Ez(x,y,z0+δ/2) * dS =
par (225) :
Ez(x0,y0,z0+δ/2) * δ 2
Passons maintenant à l'autre surface orientée en z. Elle est telle que :
dS→ = - dS * 1→z ⇒ ... ⇒
∮sz E→ . ( - dS * 1→z ) =
...
- Ez(x0,y0,z0-δ/2) * δ 2
Passons maintenant aux deux surfaces orientées en y :
dS→ = dS * 1→y ⇒ ... ⇒
∮sy E→ . dS * 1→y =
...
Ey(x0,y0+δ/2,z0) * δ 2
Et ainsi de suite de suite, de sorte que le calcul des six faces donne finalement que :
1/ε0 * ρ(x→0) * δ 3 =
( Ez(x0,y0,z0+δ/2) - Ez(x0,y0,z0-δ/2) ) * δ 2 +
( Ey(x0,y0+δ/2,z0) - Ey(x0,y0-δ/2,z0) ) * δ 2 +
( Ex(x0+δ/2,z,y00) - Ex(x0-δ/2,y0,z0) ) * δ 2 ⇔
1/ε0 * ρ(x→0) =
( Ez(x0,y0,z0+δ/2) - Ez(x0,y0,z0-δ/2) ) / δ +
( Ey(x0,y0+δ/2,z0) - Ey(x0,y0-δ/2,z0) ) / δ +
( Ex(x0+δ/2,z0,y0) - Ex(x0-δ/2,y0,z0) ) / δ
Or chacun des trois membres de cette somme n'est autre qu'une dérivée (partielle) "au centre", qui n'est qu'une variante de la traditionnelle dérivée (partielle) "à droite" : par (81) :
df(x) / dx =
limδ→0 ( f(x+δ) - f(x) ) / δ =
limδ→0 ( f(x+δ/2) - f(x-δ/2) ) / δ
de sorte que :
1/ε0 * ρ(x→0) =
∂Ex / ∂x |x0,y0,z0 +
∂Ey / ∂y |x0,y0,z0 +
∂Ez / ∂z |x0,y0,z0
(NB : les delta ronds ∂ spécifiques aux dérivées partielles.)
qui est bien la version locale recherchée, exprimant x→0 en fonction de (x0,y0,z0) ⇔ ρ et E→ ne sont considérés qu'en un seul point de l'espace. Et comme celui-ci peut se situer n'importe où dans l'espace, le zéro est en fait inutile ⇒
1/ε0 * ρ(x→) =
∂Ex / ∂x +
∂Ey / ∂y +
∂Ez / ∂z ≡ div(E→)
Divergence
Cette somme des dérivées partielles des composantes d'un champ est appelée "divergence du champ" et notée div(E→) (E→ pour le champ électrique, F→ quand le type de champ n'est pas spécifié).
Or nous avons d'autre part que :
1/ε0 * ρ(x→) =
1/ε0 * ρ(x→) * δ 3 / δ 3 =
par (226) :
limVS→0 1 / δ 3 * ∮s E→ . dS→ ⇔
limVS→0 1 / VS * ∮s E→ . dS→ = ρ(x→) / ε0 = div(E→)
qui est donc la forme locale de la loi de Gauss. Son interprétation physique s'énonce comme suit : « la divergence en un point représente le flux normalisé du champ vectoriel sur une surface fermée de taille infinitésimale entourant ce point ("normalisé" signifiant ici "divisé par le volume enfermé par la surface fermée") ».
On notera qu'en supprimant le passage à la limite et en faisant passer VS dans le membre de droite on retrouve l'interprétation de la loi de Gauss sous sa forme intégrale :
∮s E→ . dS→ = 1/ε0 * ρ(x→) * VS ⇔
∮s E→ . dS→ = 1/ε0 * ρ(x→) * ∫vS dV (224)
Observons enfin la différence entre définition mathématique (générale) et interprétation physique (particulière) de la divergence :
- div(E→) ≡ ∂Ex / ∂x + ∂Ey / ∂y + ∂Ez / ∂z (228) est la définition strictement mathématique de la divergence ;
- div(E→) = limVS→0 1 / VS * ∮s E→ . dS→ = 1/ε0 * ρ(x→) (229) en est une interprétation physique.
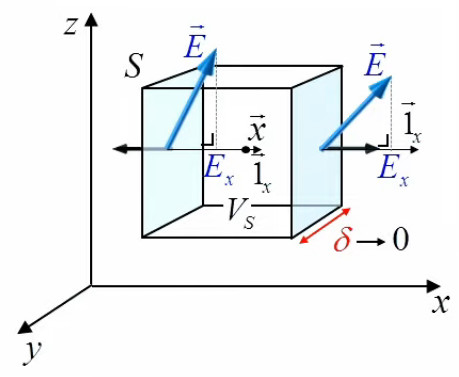
Cas particulier : dans le vide il n'y a pas de charge (par définition du vide) ⇒
ρ(x→) = 0 ⇒ div(E→) = 0 (cf. supra l'évocation de la divergence dans la démonstration du théorème de Gauss (216) ).
Application. Soit le champ :
E→(x,y,z) = a * y2 * 1→x + 2 * a * x * y * 1→y ⇒
où :
• ∂(a*y2)/∂x = 0
• ∂(2*a*x*y2)/∂y= 2 * a * x
⇒ par (228) :
div(E→) = 2 * a * x ⇒
ρ(x→) = ε0 * div(E→) = ε0 * 2 * a * x
Nabla. On obtient enfin la forme la plus fréquente de la loi de Gauss en introduisant la notion de nabla (∇→), qui correspond à la formulation du gradient (93) sans mention de fonction :
∇→ = ∂ / ∂x * 1→x + ∂ / ∂y * 1→y + ∂ / ∂z * 1→z
⇒ soit :
E→ = Ex * 1→x + Ey * 1→y + Ez * 1→z ⇒ par (59) :
∇→ . E→ = ∂Ex / ∂x +
∂Ey / ∂y +
∂Ez / ∂z ⇒ par (228) :
div(E→) = ∇→ . E→
⇒
∇→ . E→ = 1/ε0 * ρ
où :
• ε0 est la permittivité du vide (218)
• ρ est la densité volumique de charge (223)
Théorème d'Ostrogradski
Ce théorème, qui relie flux et divergence, énonce que « l'intégrale de flux d'un champ vectoriel F→ sur une surface fermée F est donnée par l'intégrale de la divergence de ce champ sur le volume VS enfermé par cette surface » : ∮s F→ . dS→ = ∮vS div(F→) * dV.
La démonstration s'obtient à partir du système d'équation exprimant le passage de la forme continue à la forme locale de la loi de Gauss:
continue :
∮s E→ . dS→ = 1/ε0 * ∫VS ρ(x→) * dV
(224)
locale :
div(E→) = ρ(x→) / ε0
(229)
En isolant ρ(x→) dans (229) et en le substituant dans (224) ⇒ annulation des deux ε0 ⇒
∮s E→ . dS→ = ∮vS div(E→) * dV
CQFD
On note le champ E→ dans le cas du champ électrique, et F→ lorsqu'on ne spécifie pas de quelle type de champ il s'agit.
Comprenons bien le caractère étonnant du théorème d'Ostrogradski :
∮s F→ . dS→ = ∮vS div(F→) * dV
: alors que le membre de droite concerne tous les points constituant le volume, le membre de gauche ne concerne que les valeurs de F→ à la surface de ce volume. Il en résulte un fait à priori contre-intuitif : quelle que soit la situation (orientation) des champs à l'intérieur du volume – situation qui détermine la valeur de div(F→) – l'intégrale de ces div(F→) est constante (et vaut la valeur donnée par le membre de gauche).
Nous allons montrer que la nature a priori contre-intuitive de ce résultat n'est qu'apparente. Mais avant il est utile d'approfondir notre compréhension intuitive de la divergence, en montrant que son interprétation physique :
div(F→) = ( limVS→0 1 / VS ) * ∮s F→ . dS→ (229)
recouvre bien sa définition mathématique :
div(F→) ≡ ∂Fx / ∂x +
∂Fy / ∂y +
∂Fz / ∂z (228).
Pour ce faire on va prendre le cas de la composante en x de la définition mathématique. À celle-ci correspondent les deux faces du cube orientées en x.
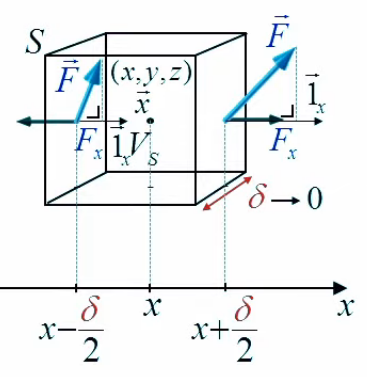
La somme des flux passant par ces deux faces est donnée par (227) :
∫ 2sx F→ . dS→ = Fx(x+δ/2,y,z) * δ2 - Fx(x-δ/2,y,z) * δ2 ⇔
∫ 2sx F→ . dS→ = [ Fx(x+δ/2,y,z) - Fx(x-δ/2,y,z) ) ] * δ2 ⇔
∫ 2sx F→ . dS→ = [ Fx(x+δ/2,y,z) - Fx(x-δ/2,y,z) ) ] / δ * δ3 ⇔
où l'on constate que la partie surlignée en jaune correspond bien à la définition d'une dérivée (centrée) : le différentiel de valeur d'une fonction entre deux points séparés d'une distance δ, divisé par δ (de sorte que le δ2 du numérateur devient δ3). Quant à y et z, ils sont constants : on circule sur la ligne reliant les trois points x-δ/2x, x et x+δ/2.
Pour passer à la surface totale du cube il faut prendre en compte les deux autres paires de surface, orientées en y et z. Cette généralisation est triviale puisqu'il y a symétrie en x, y et z ⇒
∮s F→ . dS→ = [ ∂Fx / ∂x + ∂Fy / ∂y + ∂Fz / ∂z ] * Vs ⇔
1/Vs * ∮s F→ . dS→ = [ ∂Fx / ∂x + ∂Fy / ∂y + ∂Fz / ∂z ] ⇔
1/Vs * ∮s F→ . dS→ = div(F→)
où l'on retrouve bien (229).
Poursuivons l'interprétation physique de la divergence en analysant le cas d'une dérivée partielle positive. Cela signifie que le flux entrant est plus petit que le flux sortant (cf. graphique supra). Or le flux entrant étant négatif et le flux sortant positif (210), il en résulte que le flux net est positif. L'approche mathématique de dérivée partielle positive est donc bien cohérente avec l'interprétation physique de flux normalisé net qui est positif.
Fermons cette parenthèse sur l'interprétation intuitive de la divergence, et étudions de plus près le théorème d'Ostrogradski. Nous allons montrer que le théorème contient l'interprétation physique de la divergence. Il suffit pour cela de faire tendre VS vers zéro ⇒ div(F→) ne varie qu'infiniment peu ⇒ elle peut être considérée comme constate, et donc extraite hors de l'intégrale : soit :
∮s F→ . dS→ = ∮ vS→0 div(F→) * dV ⇒
∮s F→ . dS→ = div(F→) * ∮ vS→0 dV ⇔
∮s F→ . dS→ = div(F→) * VS ⇔
1/ VS * ∮s F→ * dS→ = div(F→)
où l'on retrouve bien (229).
Venons-en maintenant à l'objectif que nous nous étions fixé au début de cette section : montrer que le caractère contre-intuitif du théorème d'Ostrogradski n'est qu'apparent. Pour ce faire on va faire la démarche inverse à celle que l'on vient de présenter : retrouver le théorème à partir de la définition/interprétation physique de la divergence.
Pour ce faire on va décomposer le volume VS en petits cubes de volume ΔVn et de surface Sn tels que n=1,2,3,...,N. On a alors que, pour chaque petit cube de vecteur position x→n :
div(F→)|xn→ = limΔVn→0 1/ ΔVn * ∮sn F→ . dS→
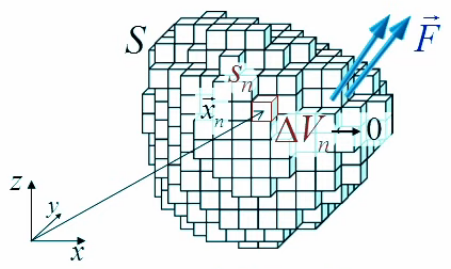
Le graphique ci-dessous représente les champs situés au milieu des six faces d'un cube. Il illustre le fait que pour chaque cube il y aura six calculs à effectuer.
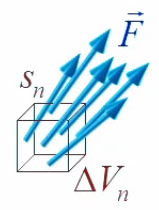
On fait passer ΔVn dans le membre de gauche ⇒ :
div(F→)|xn→ * limΔVn→0 ΔVn = ∮sn F→ . dS→ ⇒
∑n=1Ndiv(F→)|xn→ * limΔVn→0 ΔVn = ∑n=1N ∮sn F→ . dS→ ⇔
∫ vS div(F→) * dV = ∑n=1N ∮sn F→ . dS→
NB : avec la notation intégrale le |xn→ est implicite.
La conversion du membre de droite en intégrale semble plus problématique car la somme qui y est représentée prend en compte toutes les surfaces de tous les cubes, or l'intégrale de surface ne doit prendre en compte que les seules surface externes. Mais en réalité le problème ne se pose pas. Pour s'en rendre compte prenons le cas de deux cubes adjacent Sn-1 et Sn.
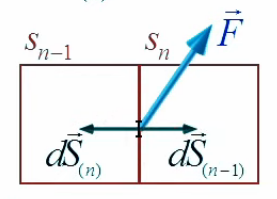
Leurs faces connexes ont une contribution au flux qui est nulle car leurs vecteurs de surface dS→ respectifs sont égaux en valeur absolue (puisque qu'ils correspondent à un même point de champ) mais de signes opposés (puisque le flux est rentrant dans un cas et sortant dans l'autre) ⇒ les produits scalaires correspondant s'annulent.
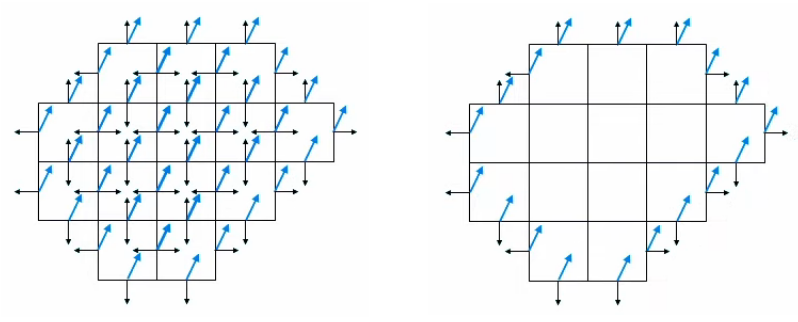
Vue en coupe ⇒ seuls 4 dS→ par cube sont représentables.
Paradoxe résolu ! Et c'est évidemment cette propriété qui dissipe l'apparente contre-intuitivité du théorème d'Ostrogradski : quelle que soit la valeur des F→ internes (norme et direction), ceux-ci sont de toute façon annulés !
On peut donc passer à l'intégrale dans le membre de droite :
∫ vS div(F→) * dV = ∑n=1N ∮sn F→ . dS→ ⇔
∫ vS div(F→) * dV = ∮s F→ . dS→
(233)
⇔ l'intégrale de la divergence sur un volume est donné par l'intégrale de flux de la fonction sur la surface qui limite ce volume. Il s'agit là d'un outil de calcul mathématique très utilisé en physique.
Méthode de Gauss : la sphère
Nous allons montrer ici que la loi de Gauss ∮s E→ . dS→ = 1/ε0 * ∫VS ρ(x→) * dV (224) permet de calculer le champ électrique E→ (membre de gauche, qui est une intégrale de surface) à partir de la distribution de charges qui en est à l'origine (membre de droite, qui est une intégrale de volume). Cette technique est appelée "méthode de Gauss". Nous allons l'illustrer ici par le cas d'un sphère chargée avec une densité volumique de charge ρ (223) constante (dans l'espace et le temps). Cette distribution de charge génère partout dans l'espace un champ électrique E→( x→), considéré au vecteur position x→.
Pour calculer ce champ on pourrait utiliser la formule du champ de Coulomb E→ = q / ( 4 * π * ε0 * r 2 ) * 1r→ (220). Une charge q contenue dans un volume infinitésimal peut être considérée comme ponctuelle. La loi de Coulomb permet alors de calculer la valeur du champ généré par cette charge en un point située à une distance r.
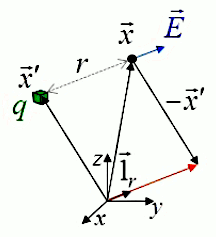
Pour connaître r il suffit de connaître la position des deux points dans un référentiel arbitraire. Le graphique ci-dessous montre comment, par construction, on trouve que :
• r = || x→ - x→' ||
• 1→r = ( x→ - x→' ) / || x→ - x→' ||
⇒
E→ = q / ( 4 * π * ε0 ) * ( x→ - x→' ) / || x→ - x→' ||3
On peut alors reconstituer la sphère par intégration de ces petits cubes, chacun générant sont propre champ en x→ ⇒ en sommant ces champs on obtient le champ généré par la sphère en x→ (principe de superposition). À chaque vecteur position x→' est ainsi associé un volume infinitésimal dV' dont la charge est alors donnée par le produit de ce volume par la densité volumique ρ : q = ρ * dV' (223). Et si la charge est infinitésimale (c-à-d arbitrairement petite), il en va de même pour le champ qu'elle génère ⇒ il faut remplacer E→ par dE→.
L'égalité précédente devient donc :
dE→ = ρ * dV' / ( 4 * π * ε0 ) * ( x→ - x→' ) / || x→ - x→' ||3
⇒ le champ généré par la sphère est donc :
E→ = ∫ dE→ = ∫ ρ * dV' / ( 4 * π * ε0 ) * ( x→ - x→' ) / || x→ - x→' ||3 ⇔
E→ = ∫ dE→ = ∫ ρ(x→') / ( 4 * π * ε0 ) * ( x→ - x→' ) / || x→ - x→' ||3 * dV'
où l'on précise que la charge volumique ρ(x→') n'est pas constante en toutes généralités (NB : ne pas confondre la sphère chargée et la surface de Gauss qui l'entoure).
Cependant le calcul de cette intégrale de volume complexe n'est pas du tout aisé. Heureusement, la loi de Gauss ∮s E→ . dS→ = 1/ε0 * ∫VS ρ(x→) * dV (224) permet de développer une méthode de calcul nettement plus simple, appelée "méthode de Gauss".
Dans le graphique suivant, la surface de Gauss S et le volume qu'elle renferme VS sont représentés en blanc.
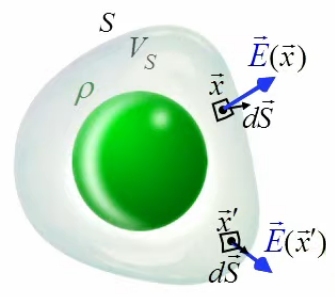
Dans l'équation supra on constate que le champ E→ que l'on souhaite calculer se trouve à l'intérieur d'une intégrale. Comment faire pour l'isoler dans le membre de gauche ? Pour répondre à cette question considérons le cas général ∫0L f(x) dx = I. On ne peut le résoudre en f(x) que si l'on considère cette fonction comme constante f(x)=f ⇒
f * ∫0L dx = I ⇔
f * L = I ⇔
f = I / L
La méthode de Gauss est fondée sur ce principe : faire en sorte que l'intégrante E→ soit une constante. Et pour ce faire on va choisir une surface de Gauss qui a cet effet. Intuitivement on devine que cette surface induit la symétrie de la distribution des charges, et qu'en l'occurrence il s'agit donc d'une sphère centrée sur, et entourant, la sphère chargée.
Le schéma suivant, qui représente la sphère en 2D, montre que le champ d'une distribution de charges sphérique et uniforme (paires de charges diamétralement opposées relativement au rayon passant par le point de champ x→) est radial, c-à-d situé sur le rayon correspondant, et donc perpendiculaire à la surface de Gauss ⇒ les dS→ sont parallèles aux E→, ce qui va simplifier le calcul du produit scalaire du membre de gauche de (224).
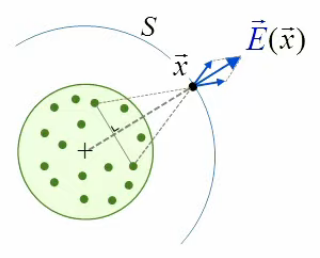
Et comme la sphère de Gauss est centrée sur la sphère chargée il en résulte que les modules E(r) des champs E→ sont égaux en tous points de la surface de Gauss :
• E→ = E(r) * 1→r
et il en va de même de leurs vecteurs de surface :
• dS→ = dS * 1→r
de sorte que :
E→ . dS→ = E(r) * dS ⇒
∮s E→ . dS→ = ∮s E(r) * dS ⇒
NB : le caractère vectoriel (et donc variable) de l'intégrale a disparu ⇒
∮s E→ . dS→ = E(r) * ∮s dS ⇒
∮s E→ . dS→ = E(r) * S ⇒
∮s E→ . dS→ = E(r) * 4 * π * r2
Il reste à calculer le membre de droite de ∮s E→ . dS→ = 1/ε0 * ∫VS ρ(x→) * dV
(224). Attention, ρ est considérée comme constante dans toute la sphère chargée, mais cela n'implique pas que ρ(x→) est constante dans la sphère de Gauss ("le volume VS enfermé par la surface de Gauss S"), qui englobe la sphère chargée. Cependant, dans l'espace différentiel c'est le vide ⇒ ρ = 0 ⇒ l'intégrale de droite, qui concerne la sphère de Gauss (de rayon r), peut être ramenée à la seule sphère chargée (de volume VSc et rayon R) ⇒
1/ε0 * ∫VS ρ(x→) * dV = 1/ε0 * ∫VSc ρ * dV ⇔
1/ε0 * ∫VS ρ(x→) * dV = 1/ε0 * ρ ∫VSc dV ⇔
1/ε0 * ∫VS ρ(x→) * dV = 1/ε0 * ρ * VSc ⇔
1/ε0 * ∫VS ρ(x→) * dV = 1/ε0 * ρ 4/3 * π * R3
de sorte que par (234), (235) et (224) :
E(r) * 4 * π * r2 = 1/ε0 * ρ 4/3 * π * R3 ⇔
E(r) = ρ * R3 / ( 3 * ε0 * r2 ) ⇔
E→ = ρ * R3 / ( 3 * ε0 * r2 ) * 1→r ⇔
E→ = ρ * VSc / ( 4 * π * ε0 * r2 ) * 1→r ⇒ par (223) :
E→ = Q / ( 4 * π * ε0 * r2 ) * 1→r
où l'on retrouve donc le champ coulombien (220) c-à-d généré par une charge ponctuelle. C'est là un résultat remarquable, et à priori contre-intuitif : le champ est indépendant du rayon de la sphère chargée (ce qui est pratique pour modéliser des corps dont la taille peut être associée à un point, tels que des électrons).
Rappelons cependant que cette équivalence entre lois de Coulomb et de Gauss n'est valable que dans un système statique; Dès que la charge bouge, la loi de Coulomb n'est plus valable (contrairement à la loi de Gauss, qui est donc plus générale). Mais nous verrons également que la méthode de Coulomb demeure incontournable dans des situations statiques non symétriques.
Interprétations habituelles :
• on retrouve la relation en 1/r2 que l'on avait déjà observée dans le cas d'une charge ponctuelle : plus on s'éloigne de la charge, plus le champ diminue ;
• le champ augmente avec la charge Q, ce qui est également intuitif.
Approfondissons maintenant l'analyse en étudiant le cas où r < R c-à-d lorsque le volume de Gauss est à l'intérieur de la sphère chargée. Étant donné la symétrie du système cela n'a pas d'impact sur le membre de gauche de (234), mais concernant le membre de droite il faut y remplacer R par r ⇒ (236) devient :
E→(r) = ρ * r3 / ( 3 * ε0 * r2 ) * 1→r ⇔
E→(r) = ρ / ( 3 * ε0 ) * r * 1→r
NB : on a donc plus la relation en 1/r2 !
En résumé :
Le graphe de la fonction E(r) illustre la croissance linéaire pour r ≤ R, suivie d'une décroissance en 1/r2 lorsque r devient supérieur à R.
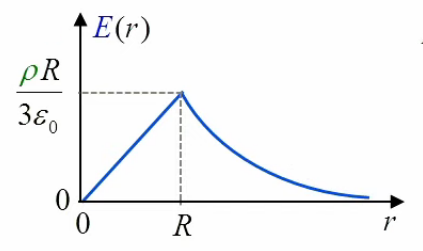
Méthode de Gauss : le cylindre
Dans la section précédente concernant l'application de la méthode de Gauss à une sphère chargée, nous avons vu que la méthode requiert d'identifier une surface de Gauss symétrique (de sorte que le produit scalaire du champ et du vecteur de surface est constant ou nul en tout point). Si la réponse est évidente dans le cas d'une sphère, elle l'est moins dans le cas d'un cylindre. Nous allons voir que dans ce cas, la méthode de Gauss fournit une approximation valable (sous certaines conditions) du champ électrique lorsque le calcul du champ se fait en un point suffisamment proche du centre du cylindre et ceci uniquement lorsque ce dernier est suffisamment long (l’approximation n’est pas quantifiée, elle n’est présentée que de façon intuitive).
Tant que l'on se situe au niveau du milieu de la longueur du cylindre chargé, il y a symétrie : le champ est perpendiculaire à l'axe du cylindre chargé. D'autre part cette perpendicularité (et partant la symétrie) est d'autant moins approximable que l'on se rapproche d'une extrémité ou l'autre.
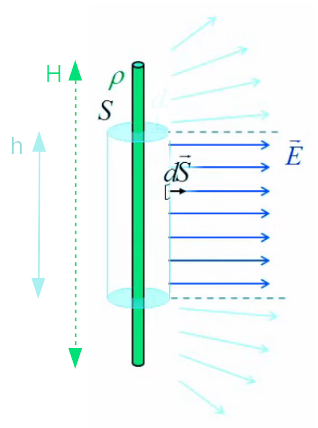
Par conséquent, si l'on considère un cylindre chargé de longueur H (en vert sur le schéma ci-dessus), et un point externe situé à la surface d'un cylindre de Gauss (en bleu) de longueur h < H et de rayon r, entourant le cylindre chargé, alors il existe au moins une valeur du ratio ( H - h ) / r au-dessus de laquelle on peut considérer que le champ généré par le cylindre chargé à la surface du cylindre de Gauss est en tous points perpendiculaire à l'axe central. C'est l'option que nous appelons symétrie localisée (et en l'occurrence "centrée").
Un autre option est celle de symétrie infinie : on considère ici une situation purement théorique (idéalisée) où H = ∞ de sorte que la symétrie n'est plus localisée, c-à-d qu'on peut la considérer en tout point de l'espace.
Quelle que soit l'option analytique choisie, ∮ étant une intégrale fermée, il faut prendre en compte la surface latérale SL ainsi que celle des deux bases du cylindre de Gauss : S = SL + SB ⇒
∮s E→ . dS→ = ∫sL E→ . dS→ + ∫sB E→ . dS→
Notez que dans le membre de droite ce ne sont plus des intégrales de surface fermée.
Concernant ∫sL E→ . dS→, le schéma ci-dessous montre la situation vue du dessus : il y a bien une symétrie radiale par rapport à l'axe du cylindre, et les vecteurs de surface dS→ sont parallèles à leur champ E→. Dans ces conditions, leur produit scalaire est égal au produit de leurs modules.
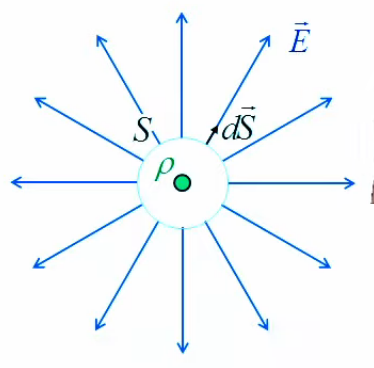
Concernant ∫sB E→ . dS→, le graphique ci-contre montre que si les deux bases sont choisies telles que perpendiculaires à l'axe du cylindre ⇒ chaque vecteur de surface est perpendiculaire à son champ, de sorte que leur produit scalaire est nul.
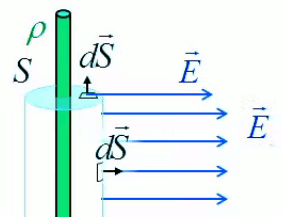
Au total on a donc que :
∮s E→ . dS→ = ∫sL E→ . dS→ + ∫sB E→ . dS→ ⇔
∮s E→ . dS→ = ∫sL E * dS ⇔
∮s E→ . dS→ = E * ∫sL dS ⇔
∮s E→ . dS→ = E * SL ⇔
∮s E→ . dS→ = E(r) * 2 * π * r * h
Pour terminer l'application de la méthode de Gauss, intéressons-nous maintenant au membre de droite de la loi de Gauss ∮s E→ . dS→ = 1/ε0 * ∫vS ρ(x→) * dV (224). Rappelons qu'il s'agit de la charge totale à l'intérieur du volume de Gauss VS. Quant à la densité de charge ρ(x→) elle est considérée comme constante (uniformément répartie) dans le cylindre chargé, mais cela n'implique pas qu'elle l'est également dans le cylindre de Gauss ("le volume VS enfermé par la surface de Gauss S"), qui englobe le cylindre chargé.
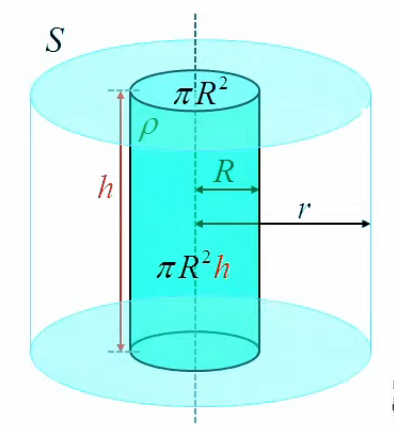
Cependant, dans l'espace différentiel c'est le vide ⇒ ρ = 0 ⇒ l'intégrale de droite, qui concerne le cylindre de Gauss (de rayon r), peut être ramenée au seul cylindre chargé (de volume VSc et rayon R), où ρ(x→) = ρ ⇒
1/ε0 * ∫vS ρ(x→) * dV = 1/ε0 * ρ ∫vSc * dV ⇔
1/ε0 * ∫vS ρ(x→) * dV = 1/ε0 * ρ VSc ⇔
1/ε0 * ∫vS ρ(x→) * dV = 1/ε0 * ρ * π * R2 * h
De sorte que par (239), (240) et (224) :
E(r) * 2 * π * r * h = 1/ε0 * ρ * π * R2 * h ⇔
E(r) = ρ * R2 / ( 2 * ε0 * r ) ⇔
E→(r) = ρ * R2 / ( 2 * ε0 * r ) * 1→r
Interprétation :
• le champ est indépendant de la longueur h du cylindre de Gauss ;
• le champ (externe) diminue en 1/r, alors que dans le cas de la sphère il diminuait en 1/r2 ⇔ la décroissance est moins rapide ;
• alors que dans le cas de la sphère la radialité était définie par rapport au centre de la sphère (r est la distance par rapport à ce point), dans le cas du cylindre elle est défini par la perpendiculaire à l'axe du cylindre (r est la distance par rapport à cet axe) ;
Densité
linéique
Dans le cas de la sphère on retrouvait le champ Coulombien (charge ponctuelle) en exprimant le champ en fonction de la charge totale Q plutôt qu'en fonction de la densité de charge ρ. A-t-on le même résultat dans le cas du cylindre ? :
par (223) :
Q = ρ * π * R2 * H ⇔
ρ * R2 = Q / ( π * H ) ⇒
substitué dans (241) ⇒
E→(r) = ( Q / H ) / ( 2 * π * ε0 * r ) * 1→r ⇒
soit λ = Q / H = ρ * π * R2 la densité linéique de charge :
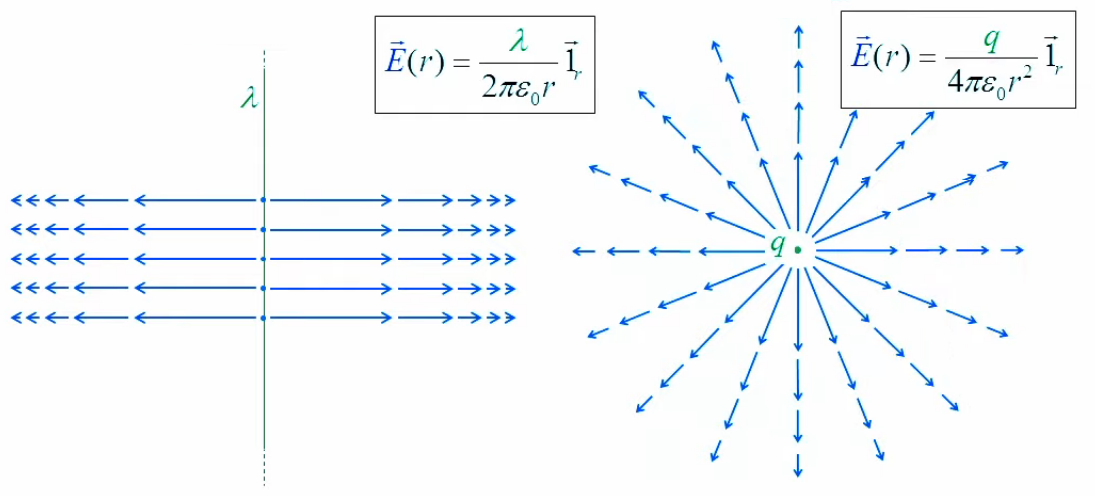
E→(r) = λ / ( 2 * π * ε0 * r ) * 1→r
De sorte que ni le rayon R ni longueur H du volume chargé n'interviennent. Dès lors, de même que la sphère chargée pouvait être théoriquement réduite à un point, le cylindre peut être théoriquement réduit à un fil rectiligne infini.
Enfin, le cas que nous venons d'analyser est tel que le rayon r du cylindre de Gauss est supérieur à celui R du cylindre chargé. Mais qu'en est-il du champ à l'intérieur du cylindre uniformément chargé, c-à-d tel que r < R ? Cette situation ne changeant rien à la symétrie, rien n'est changé concernant (239). Et dans (240) il faut juste remplacer R par r ⇒
E(r) * 2 * π * r * h = 1/ε0 * ρ * π * r2 * h ⇔
E(r) = ρ * r / ( 2 * ε0 ) ⇔
E→(r) = ρ * r / ( 2 * ε0 ) * 1→r
En résumé :
Le graphe de la fonction E(r) illustre la croissance linéaire pour r ≤ R, suivie d'une décroissance en 1/r lorsque r devient supérieur à R.
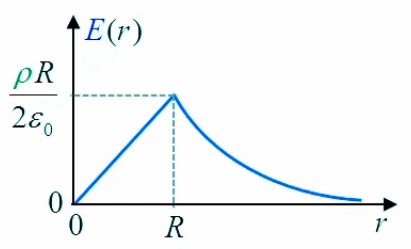
Physiquement le graphe ci-dessus peut être illustré comme dans le graphique ci-dessous : à l'intérieur du cylindre chargé le module du champ est croissant (linéairement) tandis qu'en dehors il est décroissant (en 1/r).
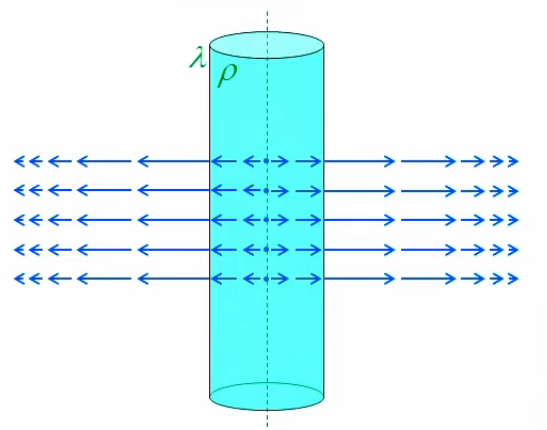
Enfin le graphique suivant compare les deux cas idéalisés : un fil de longueur infinie dans le cas du cylindre (gauche), et un point dans celui de la sphère (droite).
N.d.A. On notera que le schéma de droite peut être interprété comme celui de gauche vu d'en haut. La différence étant l'épaisseur du cylindre, qui semble pouvoir expliquer () le degré inférieur de l'exposant en r : dans les deux cas on a certes une diminution de densité, horizontalement, lorsqu'on s'éloigne du centre, mais dans le cas du cylindre la densité a une seconde dimension, verticale, qui elle ne diminue pas avec la distance au centre.
Méthode de Gauss : le plan
L'application de la loi de Gauss trouve une application notamment dans le cas de circuits électriques tels qu'un condensateur, qui n'est autre qu'un couple de plaques de charges opposées (cf. champ dipolaire), ce qui génère un champ entre les plaques (qui va permettre de contrôler les courants et tensions dans le circuit).
La problématique théorique est ici du même type que dans les deux sections précédentes. La méthode de Gauss requiert d'identifier une surface de Gauss symétrique, de sorte que le produit scalaire du champ et du vecteur de surface est constant ou nul en tout point. Si la réponse est évidente dans le cas d'une sphère (à savoir une autre sphère), elle l'est moins dans le cas d'une plaque. Nous allons voir que dans ce cas, la méthode de Gauss fournit une approximation valable du champ électrique lorsque le calcul du champ se fait en un point suffisamment proche du centre de la plaque, et pour autant que celle-ci soit suffisamment étendue et mince.
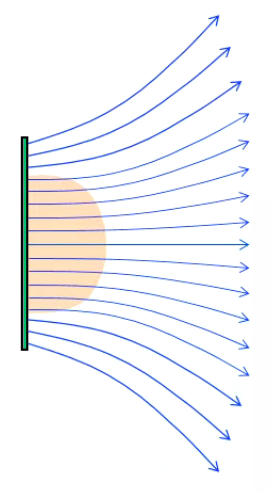
On considère ici le cas d'une plaque uniformément chargée avec une densité volume de charge ρ (223). On comprend déjà intuitivement qu'à l'instar du cylindre ce système ne présente pas la symétrie d'une sphère chargée, et que par conséquent cette symétrie devra être considérée comme localisée en le centre de la plaque, ou non localisée en supposant une plaque de superficie infinie. En effet, d'une part le champ en un point situé sur la perpendiculaire au centre d'une plaque carrée est confondu avec cet axe.
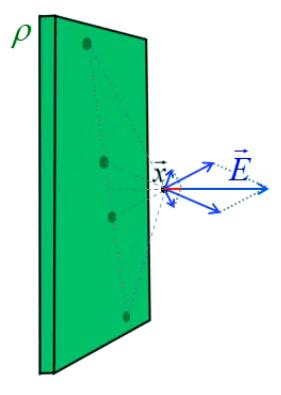
D'autre par, comme illustré par la géométrie vectorielle de l'image ci-contre, on peut considérer qu'il existe une certaine distance x à une plaque de surface L*L, en-dessous de laquelle les points sources proches du bord n'ont pas d'impact significatif sur le point de champ considéré, de sorte qu'il existe une zone centrée sur le centre de la plaque et dans laquelle le champ est uniforme c-à- identique en tout point, et en l'occurrence perpendiculaire à la plaque.
Comme dans les deux cas précédent cette limitation de symétrie locale pourra être levée en considérant le cas théorique d'une plaque de surface infinie.
La configuration du système impose logiquement la forme du volume de Gauss : celui-ci doit contenir le flux et induire une symétrie maximale ⇒ c'est donc le cylindre qui s'impose.
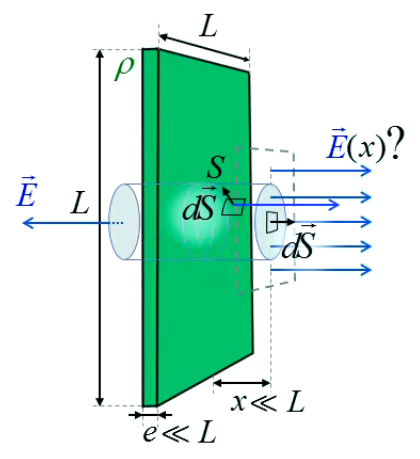
Le membre de gauche de la loi de Gauss ∮s E→ . dS→ = 1/ε0 * ∫vS ρ(x→) * dV
(224) se décompose donc à nouveau en deux intégrales de surface (non fermées) : surface latérale (SL) et celle des deux bases (2*SB) :
∮s E→ . dS→ = ∫sL E→ . dS→ + ∫sB E→ . dS→
sur la surface latérale les vecteurs de surface sont perpendiculaires à leur champ ⇒ leur produit scalaire est nul, tandis que sur les bases ils leurs sont parallèles ⇒ leur produit scalaire est égal au produit de leurs normes, ⇒
∮s E→ . dS→ = ∫sB E * dS ⇔
∮s E→ . dS→ = E * ∫sB dS ⇔
∮s E→ . dS→ = E * 2 * SB
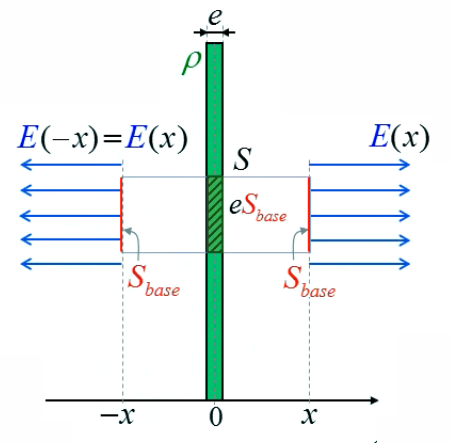
Traitons maintenant le membre de droite de la loi de Gauss ∮s E→ . dS→ = 1/ε0 * ∫vS ρ(x→) * dV
(224). C'est une intégrale de volume calculant la charge intérieure à la surface de Gauss, c-à-d la charge de la portion de plaque chargée contenue dans la surface de Gauss, ⇒ par (223) :
1/ε0 * ∫vS ρ(x→) * dV = 1/ε0 * ρ * e * SB
De sorte que par (243), (244) et (224) :
E * 2 * SB = 1/ε0 * ρ * e * SB ⇔
E = ρ * e / ( 2 * ε0 ) ⇔
E→(x) = ρ * e / ( 2 * ε0 ) * 1→⊥
NB : 1→⊥ = - 1→x vers la gauche, et 1→⊥ = 1→x vers la droite !
Interprétations :
• le champ ne dépend pas de la surface de la plaque ;
• le champ (externe) ne dépend pas de sa distance x à la plaque : quelle que soit la distance à laquelle on se trouve de la plaque chargée le champ est constant !
Densité
surfacique
Dans le cas de la sphère on retrouvait le champ Coulombien (charge ponctuelle) en exprimant le champ en fonction de la charge totale Q plutôt qu'en fonction de la densité de charge ρ. A-t-on le même résultat dans le cas de la plaque ? Par (223) :
Q = ρ * e * S ⇔
ρ * e = Q / S ⇒ substitué dans (245) :
E→(x) = Q / S / ( 2 * ε0 ) * 1→⊥ ⇒
soit σ = Q /S = ρ * e la densité surfacique de charge :
E→(x) = σ / ( 2 * ε0 ) * 1→⊥
De sorte que ni l'épaisseur e ni la surface S de la plaque n'interviennent. Dès lors, de même que la sphère chargée pouvait être théoriquement réduite à un point, et le cylindre à un fil rectiligne infini, la plaque peut l'être à un plan d'extension infinie et infiniment mince.
Enfin, le cas que nous venons d'analyser est tel que le champ est à l'extérieur de la plaque, mais qu'en est-il à l'intérieur ? Cette situation ne changeant rien à la symétrie, rien n'est changé concernant (243). Et dans (244) il faut juste remplacer e par 2*x ⇒
E * 2 * SB = 1/ε0 * ρ * 2 * x * SB ⇔
E = ρ / ε0 * x ⇔
E→(x) = ρ / ε0 * x * 1→⊥
Ainsi alors que le champ était indépendant de x en dehors de la plaque, ce n'est plus le cas dans celle-ci (on avait donc raison de faire preuve de prudence dans (245), en mentionnant E→(x) plutôt que E→). En particulier le champ est nul si x=0 c-à-d lorsqu'on on se situe au milieu de la plaque, ce qui est logique puisque cette situation est symétrique.
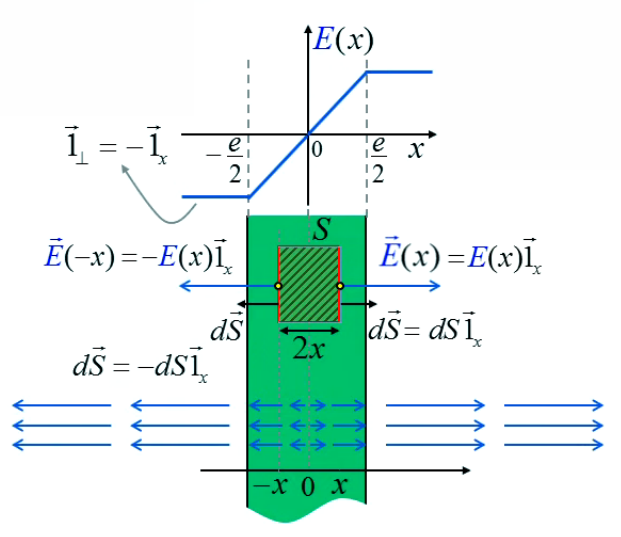
On notera une continuité (intuitive) dans la dépendance du champ externe à la distance r au volume chargé, selon la forme idéalisée de celui-ci :
• source ponctuelle (dim=0) : dépendance en 1/r2 ;
• source linéaire (dim=1) : dépendance en 1/r1 ;
• source plan (dim=2) : dépendance en 1/r0=1 c-à-d indépendance ;
que l'on peut généraliser par source de dim = n ⇒ dépendance en 1 / r (2-n).
Dans le cas du plan, le résultat à priori contre-intuitif de non dépendance du champ externe par rapport à la distance n'est qu'apparent :
• horizontalement (c-à-d dans le sens du flux) : pas de radialité horizontale, donc pas de baisse de densité lorsqu'on s'éloigne du centre ;
• verticalement (c-à-d perpendiculairement au flux) : il y a une épaisseur de flux de sorte que la densité est logiquement constante dans l'espace.
Mais rappelons-nous que ces résultats ne valent que pour une distance proche du corps chargé : au delà on retrouvera une dépendance tendant vers 1/r2 au fur et à mesure que la distance grandit c-à-d que l'objet chargé devient petit relativement à celle-ci.
Potentiel
2. Gravitation universelle
3. Potentiel et résistance électrique
6. Potentiel coulombien
7. Champ et gradient du potentiel
8. Équations de Poisson et Laplace
Potentiel gravitationnel
Le potentiel permet de décrire les aspects énergétiques d'un champ de forces. Comme introduction au concept de potentiel électrique, nous allons ici étudier la notion de potentiel gravitationnel. Pour ce faire on va étudié le cas d'une boule qui, dévalant une pente, acquiert ainsi une énergie cinétique.
Quelle vitesse faut-il imprimer à une boule située au bas d'une pente de longueur et pente déterminées pour qu'elle en atteigne le sommet ? Pour résoudre ce problème, commençons par identifier la loi physique générale auquel ce problème fait référence. En l'occurrence il s'agit de la loi de conservation de l'énergie : l'énergie ne se créé ni ne se perd, elle ne peut que se transformer d'une forme en une autre. Ainsi l'énergie cinétique que la boule acquiert en dévalant la pente n'est en réalité que la transformation de l'énergie potentielle qui lui a été conférée par le travail qu'il a fallu exercer pour l'amener en haut de la pente.
Énergie
potentielle
Ensuite il s'agit d'identifier la loi particulière à ce problème. En l'occurrence il s'agit du fait que le travail à fournir pour élever une masse m à une hauteur h est indépendant de l'angle que fait avec le sol la pente par laquelle la masse est élevée (c-à-d indépendant de la longueur du chemin choisi).
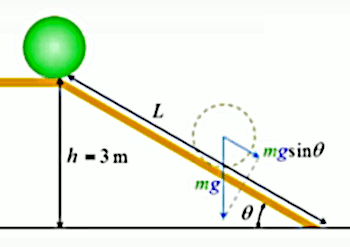
Démonstration :
si θ=π/2 ⇒ par (173) :
W = F * L et par (58) :
W = F * L * cos(π/2-θ) ⇒ par (33) :
W = F * L * sin(θ) ⇒ par (168) :
W = m * g * L * sinθ ⇒ par (34) :
W = m * g * h ⇔
W = m * g * z
(z est souvent utilisé pour exprimer une variable de hauteur, et h pour exprimer une donnée de hauteur).
En vertu du principe de conservation ce travail est donc stocké dans la boule, sous forme d'énergie potentielle Ep telle que :
ΔEp = W = m * g * z
Ce processus est évidemment réversible : si cette boule est ensuite relâchée au sommet de la pente à une vitesse initiale nulle, alors elle se met à dévaler la pente, en transformant son énergie potentielle en énergie cinétique Ec = m * v2 / 2 (185), c-à-d en acquérant de la vitesse (ici à accélération constante). Donc, à nouveau le principe de conservation :
| Δ Ep | = | - Δ Ec | ⇔
m * g * z = m * v2 / 2 ⇔
v = √(2 * g * z)
Ainsi pour toute hauteur z, on peut calculer la vitesse correspondant v(z) (g étant donnée). Et v(z=h) est donc donc la vitesse qu'il faut imprimer à la boule immobile en bas de la pente pour l'y amener au sommet.
Si on fait abstraction des forces de frottement ⇒ la vitesse maximale de la boule qui arrive en bas de la pente reste constante ⇒ on est dans un MRU ⇒ la boule continue indéfiniment sur sa lancée (et on aurait eu également un MRU sur le plateau si la vitesse initiale en bas de la pente avait été supérieure à v(z=h) ). Autrement dit, la vitesse minimale à imprimer pour le trajet bas-haut est la vitesse maximale à la fin du trajet haut-bas, dans le cas d'une boulée lâchée à une vitesse initiale nulle.
Un résultat à priori contre-intuitif de v = √(2 * g* z) (249) est que cette vitesse est indépendante de la masse : quelle que soit celle-ci, la vitesse initiale sera identique pour l'amener en haut de la pente ! On voit que la vitesse ne dépend que du produit g * z, que l'on appelle "potentiel gravitationnel" (noté VG), et que l'on définit plutôt en fonction de l'énergie potentielle équivalente au travail fourni pour gagner ce potentiel :
Ep = W = m * g * z (248) ⇒
VG = Ep / m = g * z [J/kg]
qui est donc l'énergie potentielle par unité de masse, caractérisant ainsi le champ gravitationnel dans sa dimension énergétique : à chaque hauteur z correspond une valeur de VG, laquelle est indépendante de la masse de l'objet considéré (puisque, précisément, c'est l'énergie potentielle par unité de masse). Ainsi pour connaître l'énergie potentielle d'un corps à une hauteur z, il suffit de multiplier sa masse par le potentiel gravitationnel correspondant à cette hauteur.
Découle alors logiquement de la notion de potentiel, celle de différence de potentiel entre deux niveaux de hauteur, qui permet de procéder à des bilans énergétiques. Ainsi le travail à fournir pour déplacer une masse entre deux niveaux quelconques – c-à-d l'énergie potentielle ΔEp ainsi gagnée – vaut m * ΔVG où ΔVG = VGf - VGi (f pour "final" et i pour "initial").
N.B. La hauteur (en m, km, ...) à laquelle on place le zéro de l'échelle du potentiel (en J/kg) n'a donc aucune importance (notamment, le potentiel zéro ne doit pas nécessairement correspondre à la hauteur zéro) : ΔVG = m * ( zf - zi ) où zf et zi sont les hauteurs finale et initiale.
Application. Le skieur de 80kg qui a dévalé une pente quelconque, et dont l'altitude a ainsi baissé de 3m, a perdu une énergie potentielle de 80 * ( 10 - 40 ) = 80 * ( 0 - 30 ) = ... = -2.400J, laquelle s'est transformée en différentiel d'énergie cinétique de même valeur absolue mais de signe opposé.
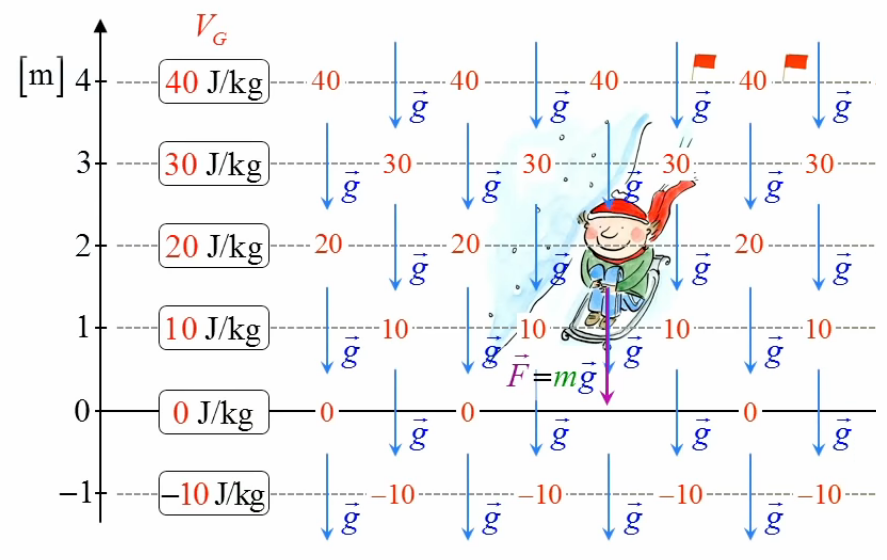
Ainsi pour le trajet haut-bas, le travail fournit est négatif c-à-d que l'on reçoit du travail (principe des barrages hydroélectriques). Cependant, la notion de travail négatif étant peu intuitive, on parle plutôt de différence négative d'énergie potentielle.
Ainsi le principe de conservation de l'énergie se formule par :
ΔEp + ΔEc = 0 ⇔
mΔVG + ΔEc = 0
Bilan énergétique. La notion de potentiel gravitationnel vient ainsi compléter celle de champ (d'accélération) gravitationnel : alors que le vecteur accélération g→ caractérise le champ gravitationnel (vectoriel et uniforme) dans sa dimension de force (F = m * g), le potentiel gravitationnel peut être vu comme un champ (scalaire) qui caractérise le champ gravitationnel dans sa dimension énergétique (Ep = m * VG).
Gravitation universelle
Dans la section précédente g est considéré comme une donnée c-à-d une constante. Nous allons ici étudier la nature de cette constante, et ainsi constater que cette donnée est relative aux référentiels planétaires, via la masse et le rayon de celles-ci.
La force de gravitation universelle :
f→ = - m * G * M / r 2 * 1→r
où :
• M = masse de la planète ;
• G : constante de gravitation universelle ;
• r : distance par rapport au centre de la planète (encore appelée "coordonnée radiale").
De sorte que g→ = - G * M / r 2 * 1→r
⇒ plus un corps est éloigné du centre de la planète, plus son poids diminue. Cette décroissance est en 1/r2 (NB : comme le champ électrique d'une charge ponctuelle ...).
À une distance proche de la surface terrestre on peut considérer que g est une constante, de valeur de g = G * M / R 2 ≈ 9,81 m/s2 (où R=6.370km est le rayon de la Terre), car une altitude de 1.000m par rapport à la surface terrestre (par exemple) ne représente que 1/6.370≈0,2% de R ⇒ g = G * M / ( R + 1.000) 2 ≈ 9.81 m/s2.
On arrondit souvent g à 10 m/s2.
Potentiel
gravitationnel
Notons que cette hypothèse de g constant était sous-jacente dans la section précédente. Nous allons maintenant lever cette hypothèse (ce qui revient à se situer à de hautes distances de la surface de la Terre) et voir ce qu'il en devient du potentiel gravitationnel VG = Ep / m = g * z (250) lorsque le champ est variable.
Si g est variable alors F = m * g l'est aussi ⇒ W = F * L aussi. Pour calculer W on va donc devoir utiliser le calcul intégral, c-à-d additionner des dW, en posant que g est constant non plus ∀ r mais seulement ∀ dr, c-à-d ∀ Δr de taille arbitrairement petite et donc potentiellement infiniment petite.
Ainsi calculons le travail nécessaire pour déplacer la masse m entre l'altitude r (par rapport au centre de la Terre) et l'infini.
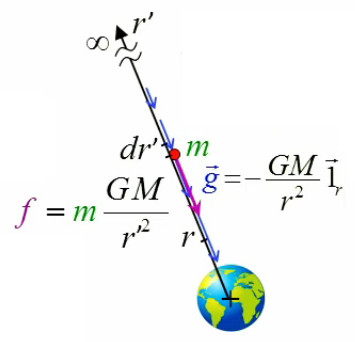
L'infini est une situation théorique qui permet ici de définir un référentiel d'énergie potentielle nulle : si r = ∞ ⇒ (251) f→ = - m * G * M / r 2 * 1→ = 0 ⇒ (173) W = F * x(t) = 0 ⇒ (248) Ep = W = 0 : l'infini équivaut au vide intersidéral, de sorte que la masse en question n'y a plus d'interaction avec la Terre.
Rappel : dans la section précédente nous avons vu que la hauteur à laquelle on place le zéro de l'échelle du potentiel n'a aucune importance ⇒ on peut le placer où l'on veut, notamment à l'infini.
W = ∫r∞ dW ⇔ par (248) :
W = ∫r∞ m * g * dr' ⇔ par (252)
NB : notez la distinction à faire entre la variable de position r' et le r de l'intégrale qui est la valeur de départ.
W = ∫r∞ m * G * M / r' 2 * dr' ⇔
W = m * G * M * ∫r∞ 1 / r' 2 * dr' ⇔ par (98) :
W = m * G * M * [ - 1 / r' ]r∞ ⇔
W = m * G * M * / r ⇔
L'interprétation est intuitive : plus r est élevé, c-à-d plus on part de haut (zi ⇔ VGi ), moins grand est le travail à réaliser pour élever la masse jusqu'à l'infini (zf = ∞ ⇔ VGf = 0).
À l'infini on a donc que :
Ep(∞) = 0
et d'autre part le travail à fournir pour élever jusqu'à l'infini une masse m à partir d'une hauteur r (comptée à partir du centre de la Terre) vaut :
W = m * G * M * / r
or par (248) :
Ep(r) = Ep(∞) - W ⇒
Ep(r) = - m * G * M * / r ⇒
VG(r) = Ep(r) / m = - m * G * M * / r / m ⇔
VG = Ep / m = - G * M * / r
Le schéma suivant est celui de la fonction VG(r). Il illustre la notion de "puits de potentiel" : pour envoyer une masse m à l'infini à partir de la surface de la Terre il faut une énergie égale à m * G * M * / r, où G * M * / r est la profondeur du puits de potentiel, ou encore la différence de potentiel libératrice.
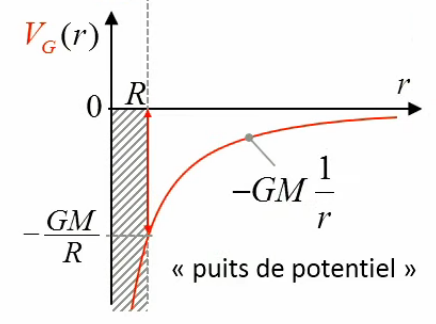
L'énergie qu'il faut mobiliser pour libérer une masse (en l'occurrence une fusée) de la gravitation terrestre est considérable. Ainsi la vitesse de libération du champ gravitationnel terrestre est la solution de l'égalité entre l'énergie cinétique et Ep(r) :
1/2 * m * v2 = m * G * M * / R ⇔
v = √(2 * G * M * / R) ⇔
v = √(2 * G * M * / R2 * R ) ⇔ par (252)
v = √(2 * g * R )
Cette vitesse, indépendante de la masse de la fusée, vaut :
√(2 * 0,01 * 6.370 ) ≈ 11,3 km/s
Le graphique suivant représente la baisse (en 1/r) du potentiel gravitationnel au fur et à mesure que l'altitude (la distance au centre de la Terre) augmente : chaque anneau représente un multiple du rayon terrestre. Il y a isotropie des équipotentiels puisque ce sont des sphères centrées sur le centre de la planète.
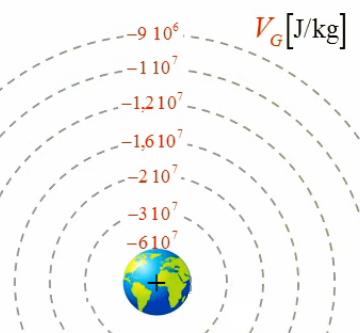
Potentiel et résistance électrique
• Résistance électrique (loi d'Ohm)
• Potentiel électrique : champ quelconque
On va s'intéresser aux potentiels associés à des champ électriques uniformes. Pour ce faire on va se mettre dans une situation comparable au champ gravitationnel, au moyen d'une plaque d'une certaine surface, située dans le vide (⇒ elle ne subit pas de gravitation), chargée négativement (par exemple en la frottant). La méthode de Gauss nous a montré que cette plaque génère un champ perpendiculaire à sa surface et sur une zone centrée (cf. #methode-gauss-plan). La plaque étant chargée négativement, nous savons par (207) que le champ est alors dirigé vers la plaque (des deux côtés de celle-ci (mais seul nous intéresse ici le côté "supérieur", pour l'analogie avec le champ gravitationnel). Si nous plaçons une charge q dans ce champ E→, nous savons qu'elle va y subir une force F→ = q * E→ (206).
Considérons maintenant le cas de deux billes dont l'une est chargée positivement (bille verte), tandis que la charge de l'autre est neutre (bille bleue). Vu qu'on se situe dans le vide interstellaire les deux billes sont en apesanteur. Cependant la bille verte, étant chargée négativement, est naturellement collée contre la paroi (qui est négative).
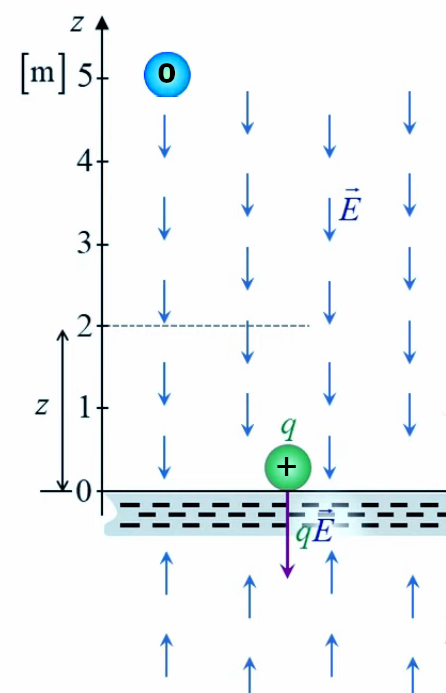
Pour éloigner la bille de la plaque (on ne dit pas lever car en apesanteur il n'y ni haut ni bas) d'une distance z, il faut combattre la force d'attraction F→ en effectuant un certain travail W = F * z = q * E * z (173), de sorte qu'à la distance z la bille a acquis une énergie potentielle EP = W. Si de la distance z on relâche la bille, celle-ci retourne vers la plaque en acquérant une vitesse v (avec accélération constante) lui donnant ainsi une énergie cinétique EC = 1/2 * m * v2 telle que EC = EP.
NB : ne pas confondre EP (énergie potentielle) et E (module du champ électrique).
Par définition, et analogie avec le potentiel gravitationnel (253), le potentiel électrique d'une charge q est :
VE = EP / q [J/C = V (volt)]
On détermine comme suit l'équation permettant de calculer le potentiel électrique V correspondant à une distance quelconque z :
VE = EP / q ⇔
VE = W / q ⇔
VE = F * z / q ⇔
VE = q * E * z / q ⇔
VE = E * z
Les équations ci-dessus sous forme différentielle :
ΔV(z) ≡ ΔEP(z) / q = E * (zf - zi)
où zf et zi sont les positions initiales et finales d'une trajectoire entre deux niveaux de potentiel.
Unité. On voit ici que la notion de volt est moins intuitive que J/C : il faut bien se rappeler que les volts ce sont des joules par coulomb, puisque la notion de potentiel sert précisément à décrire ce qu'il se passe au niveau énergétique (cf. les Joules) quand on déplace des charges dans un champ électrique !
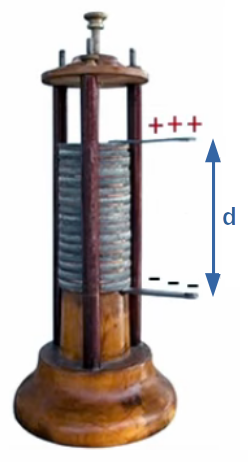
Pile de volta
Le terme volt vient du nom de l'inventeur de la pile électrique, Alessandro Volta. Comme son nom l'indique une pile électrique est une pile de disques, alternativement composés de zinc et d'argent : celui du bas était en zinc et celui du haut en argent. Ces disques étaient séparés par un buvard imbibé d'acide. Enfin les deux plaques extrêmes comportent une patte appelée "électrode". Celle en zinc (en bas) arrachant les électrons de l'argent (qui a des électrons périphériques mobiles passant facilement au zinc) est alors chargée négativement, tandis que l'électrode du haut (en argent) est chargée positivement.
Ce différentiel de charge génère un champ électrique E. Mais c'est le potentiel V = EP / q = E * d qui caractérise la pile, via la distance d entre les deux électrodes.
Le travail nécessaire pour déplacer une charge positive de l'électrode négative vers la positive est tel que :
W = F * d ⇒ par (206) :
W = q * E * d ⇒ par (256) :
W = q * V
(255)
Ainsi la connaissance du potentiel électrique V permet ainsi de faire facilement des bilans énergétiques pour des échanges de charges entre les deux électrodes. Ainsi en connaissant q et V (déterminés lors de la fabrication de la pile) on connaît alors l'énergie cinétique provoquée par le retour, sur l'électrode négative, de la charge positive qui aura été relâchée de l'électrode positive. Ainsi soit une pile de 1,5 volt de potentiel, alors une charge de 1C échangée entre les deux électrodes met en jeu une énergie de EP = q * V = 1 * 1,5J.
N.B. Pour que le champ entre les deux électrodes soit uniforme (c-à-d pour que les équations ci-dessus soit valables) il faudrait que ces électrodes soient des plaques.
L'analogie avec le potentiel gravitationnel s'applique également pour la notion de différence de potentiel : ΔEP = q * ΔV (257)
de sorte que l'énergie potentielle et le potentiel peuvent être aussi définis à une constante près. Autrement dit, il ne doit pas nécessairement avoir correspondance entre le zéro de l'échelle de distance et celui de l'échelle de potentiels. Le potentiel est donc une notion abstraite puisqu'à un même point de l'espace la valeur du potentiel sera fonction de la distance arbitraire à laquelle sera fixé le potentiel zéro !

Soit une pile de 1V de potentiel. Gauche : si le zéro est sur la borne négative, alors la borne positive est à +1V. Droite : si le zéro est placé sur la borne positive alors la borne négative est à -1V. On pourrait aussi avoir -1/2 sur la borne négative et 1/2 sur la borne positive, etc. Tous ces différents "calages" sont équivalents : Vf - Vi = 1 - 0 = 0 - (-1) = 1/2 - (-1/2) = 1 où les indices f et i sont relatifs à la force qu'il faut appliquer pour remonter le courant de la force "naturelle" du système considéré (ici la pile).
Une pile fournit donc une différence de potentiel, encore appelée "tension électrique", "force électromotrice", ou encore "voltage".
En résumé, la plaque (en bleu clair dans le schéma ci-dessous) chargée négativement génère dans son environnement :
- E→ : un champ de forces électriques E = F / q (uniformes) , de nature vectorielle (répartition spatiale de vecteurs, dont l'unité des modules est le N/C), qui modélise les forces exercées sur les charges ;
- V : un champ de potentiels électriques VE = EP / q , de nature scalaire (répartition spatiale de nombres, dont l'unité est le volt=J/C), qui informe sur la situation énergétique (bilans énergétiques).
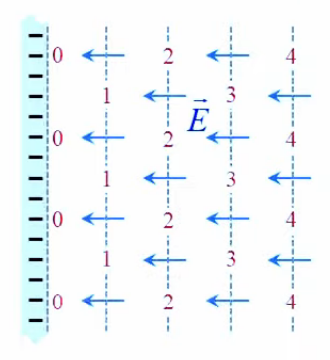
Illustration
Supposons que dans le champ de potentiels uniforme du graphique précédent, le module du champ de force uniforme est fixé à E = F / q = 2 N/C.
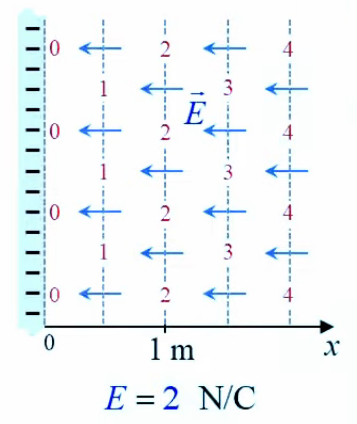
Notons que cela détermine l'échelle des distances (valeur de V à x=1) : par (256) :
V = E * x ⇒
V = 2 * x ⇒
la valeur de V pour laquelle x=1 est :
V(1) = 2 * 1 = 2
Ou, plus explicitement :
F / q = 2 ⇒ si q=1C ⇒ F=2N
⇒ le travail pour amener cette charge de 1C à une distance de 1m vaut :
2N * 1m = 2J ⇒
VE = Ep / q = W / q = 2 J/C
La fonction potentiel V(x) = E * x
(256) est donc une fonction du champ électrique, dont le module E exprime la sensibilité (pente) du potentiel par rapport à la distance. Et la connaissance du potentiel permet de connaître l'énergie des charges se trouvant dans ce potentiel. Par V(x) ≡ EP(x) / q = E * x (257) :
1 : champ de forces : V(x) = E * x
2 : champ de potentiels : EP(x) = q * V(x)
⇔ la connaissance du champ E permet de calculer le potentiel V, qui permet de calculer l'énergie EP.
Le graphe infra représente ces deux fonctions pour une charge positive q = 0,5 C.
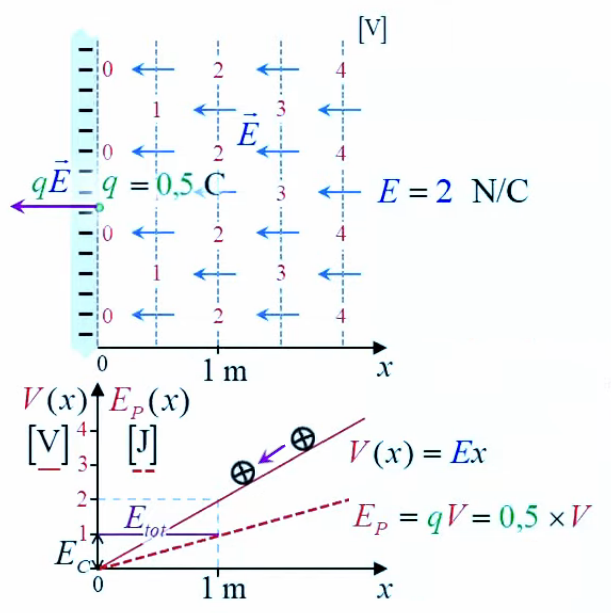
Dans le graphe ci-dessus, on voit que la pente du potentiel V(x) vaut bien 2 (module du champ électrique), et qu'en raison de la valeur de la charge (0,5 C), l'énergie potentielle vaut la moitié du potentiel (NB : les unités ne sont pas les mêmes : le potentiel est en volts, tandis que l'énergie est en joules).
L'énergie totale est représentée par une horizontale (en mauve), ce qui illustre le principe de conservation de l'énergie. La diagonale hachurée exprime alors la transformation de l'énergie potentielle en énergie cinétique au fur et à mesure que la charge se rapproche à vitesse croissante de la plaque (il y a attraction puisque plaque et charge sont de signes opposés). Cette vitesse est donc causée par la force d'attraction, et est à son tour la cause de l'augmentation (linéaire) de l'énergie cinétique : F ⇒ v ⇒ Ec.
Par analogie avec la gravitation on peut interpréter la droite du potentiel comme le flanc d'une pente où dévalent des billes (les charges positives) : une charge positive descend le potentiel, tout comme elle est tirée par le champ dans la direction de diminution du potentiel.
Procédons au bilan énergétique de cette charge positive lorsqu'elle se situe à une distance x=1 de la plaque. Pour ce faire nous avons à notre disposition deux outils : le champ et le potentiel :
- Champ : cette charge positive subit une force attractive (puisque la plaque est chargée négativement) ⇒ si elle n'est pas retenue alors elle se dirige naturellement vers la plaque (qui est donc sa localisation naturelle en absence d'autres forces) ⇒ la force d'application (qui s'oppose à la force naturelle du système) est telle que 0 = xi (lieu où la force d'application commencera à être exercée) ⇔ EP(0) = EPi.
- Potentiel :
EP(x) = q * V(x) ⇒
EP(1) = 0,5 * 2 = 1JPlus explicitement : soit la charge positive en x=0 ⇒ pour la pousser en x=1 il faut exercer un travail de :
W = F * x ⇔
W = 1 * 1 = 1J ⇔
EPf - EPi = 1J ⇔
EP(1) - EP(0) = 1J
or la distance à laquelle correspond le zéro de l'énergie est arbitraire : en l'occurrence le calage est tel que l'énergie potentielle nulle correspond à x=0 : Ep(0) = 0 ⇒
EP(1) = 1J
Tant que la charge est immobile (retenue) en x=1 il y a égalité entre son énergie potentielle et son énergie totale. Si alors on relâche la charge on constate que l'énergie potentielle diminue, au profit de l'énergie cinétique, qui augmente sous l'effet de la force d'attraction, et par l'intermédiaire de la vitesse croissante (F ⇒ v ⇒ Ec). Ce faisant, la charge négative "descend le potentiel" : en se rapprochant de la plaque elle passe par des valeurs décroissantes du potentiel.
Charge
négative
À plaque inchangée (c-à-d toujours chargée négativement), l'analogie avec la gravitation n'est plus valable dans le cas de charges négatives, puisqu'alors la force devient répulsive. Observons ce qui se passe lorsque q=-0,5C :
- Champ : cette charge subit une force répulsive ⇒ si elle n'est pas retenue, alors elle s'éloigne de la plaque ⇒ elle ne se situe donc pas naturellement en x=0 ⇒ la force d'application (qui s'oppose à la force naturelle du système) est telle que 0 = xf (lieu où la force d'application arrêtera d'être exercée) ⇔ EP(0) = EPf.
- Potentiel :
EP(x) = q * V(x) ⇒
EP(1) = -0,5 * 2 = -1J
La notion d'énergie négative est peu intuitive, mais n'oublions pas que le niveau où est placé le zéro de l'énergie est arbitraire ⇔ ce qui compte ce sont les différentiels !Ainsi, plus explicitement : soit la charge négative en x=1 ⇒ pour la pousser en x=0 il faut exercer un travail de :
W = F * x ⇔
W = 1 * 1 = 1J ⇔
EPf - EPi = 1J ⇔
EP(0) - EP(1) = 1J ⇒
0 - EP(1) = 1J ⇔
EP(1) = -1J ⇔
Et si alors en x=0 on relâche la charge on constate que l'énergie potentielle diminue, au profit de l'énergie cinétique, qui augmente sous l'effet de la force de répulsion, et par l'intermédiaire de la vitesse croissante : on a toujours F ⇒ v ⇒ Ec. La charge négative remonte ici le potentiel : en s'éloignant de la plaque elle passe par des valeurs croissantes du potentiel.
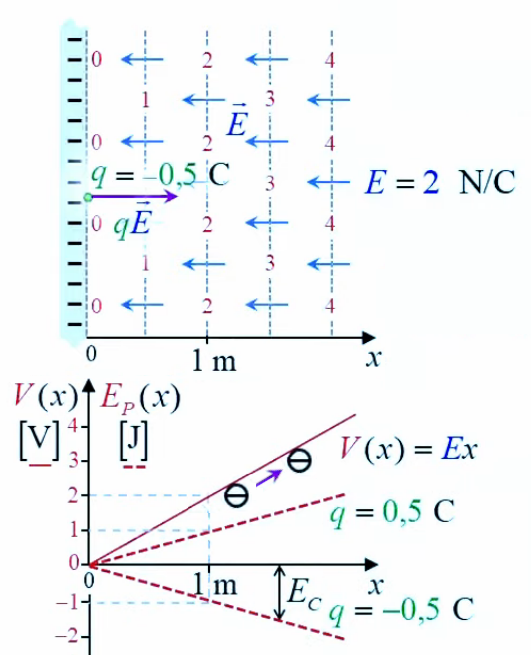
Dans le cas d'une plaque négative et d'une charge négative, la droite de l'énergie potentielle (ligne hachurée) est celle du bas.
L'analogie avec la gravitation est ici inversée : on peut voir les particules négatives comme de petites bulles d'air dans l'eau, et qui, poussées vers la droite par la force répulsive, remonteraient le long d'une paroi inclinée (la ligne continue du graphe) située juste au-dessus d'elles.
On a donc une règle générale : toute charge (quel que soit son signe) se dirige (mouvement) dans le sens de la diminution de son énergie potentielle, et donc dans le sens de l'augmentation de son énergie cinétique (mouvement). La différence c'est que les charges négatives remontent le potentiel (c-à-d vont donc contre /sont repoussées par le champ), tandis que les charges positives descendent le potentiel (c-à-d suivent /sont tirées par le champ). La direction du champ indique donc toujours la baisse du potentiel. Nous verrons plus loin que cette règle générale vaut également dans le cas d'une plaque positive.

Cette propriété de la charge négative remontant le potentiel correspond précisément à ce qui se passe dans les circuits, par exemple celui constitué par une pile dont on a relié les deux électrodes par un fil de cuivre (qui conduit l'électricité) : un courant transporte les électrons de l'électrode négative, qui remontent ainsi jusqu'à l'électrode positive. Les électrons "remontent" naturellement le champ électrique, du fond de leur puits de potentiel, en perdant de l'énergie potentielle !
Ici il n'y a donc plus analogie avec le champ gravitationnel, qui maintient la masse au fond du puis, tandis que les électrons le remontent naturellement (si les électrodes sont reliées par un conducteur). Nous avons vu que cela est du au fait qu'on peut donner un signe différent aux charges, tandis que la masse est toujours positive.
Mais en remontant le potentiel les électrons de la pile perdent de leur l'énergie potentielle. Pourtant leur vitesse est constante, ce qui implique qu'ils ne gagnent pas d'énergie cinétique. Comment cela est-il possible, puisqu'il y a conservation de l'énergie ? La réponse est qu'il y a bien conservation, mais que la transformation peut se faire vers diverses forme d'énergies alternatives. En l'occurrence l'énergie potentielle ne se transforme pas en énergie cinétique mais en énergie thermique c-à-d en chaleur. C'est l'effet Joule : une résistance liée à une source de tension produit de la chaleur (principe du chauffage électrique).
Plaque +
Charge +
Passons maintenant au cas d'une plaque positive. Dans ce cas le champ est extraverti (207). Considérons le cas d'une charge d'essai positive q=0,5C, toujours dans un champ tel que E = F / q = 2 N/C.
- Champ : cette charge positive subit une force répulsive ⇒ la charge n'est pas naturellement contre la plaque ⇒ la force d'application (qui s'oppose à la force naturelle du système) est telle que 0 = xf (lieu où la force d'application arrêtera d'être exercée) ⇔ EP(0) = EPf.
- Potentiel : soit la charge située en x=1 ⇒ pour la ramener sur la plaque (c-à-d en x=0) il faut exercer un travail :
W = F * x ⇒
W = 1 * 1 = 1J ⇒
EPf - EPi = 1J ⇔
EP(0) - EP(1) = 1J ⇔
0 - EP(1) = 1J ⇔
EP(1) = -1J ⇒
V(1) = EP(1) / q ⇔
V(1) = -1 / 0,5 = -2J
Analyse :
• le graphe de EP est celui correspondant à plaque et charge négatives ;
• le graphe de V est le symétrique de celui de la plaque négative ⇒ le champ de potentiels est le même que celui de la plaque négative au signe près.
La règle générale supra se complète donc par une propriété supplémentaire : lorsqu'on s'éloigne de la plaque, une plaque positive génère donc dans son espace environnant un potentiel qui diminue (dans les valeurs négatives), tandis qu'une plaque négative génère un potentiel qui augmente (dans les valeurs positives).
Plaque +
Charge -
- Champ : cette charge négative subit une force attractive (puisque la plaque est chargée positivement) ⇒ elle est naturellement contre la plaque c-à-d en x=0 ⇒ la force d'application (qui s'oppose à la force naturelle du système) est telle que 0 = xi (lieu où la force d'application commencera à être exercée) ⇔ EP(0) = EPi.
- Potentiel : puisque l'on connaît le potentiel de la plaque en x=1, on peut aller plus vite pour ce second point :
EP = q * V ⇒
EP(1) = -0,5 * V(1) ⇒
EP(1) = -0,5 * -2 = 1J
Plus explicitement : soit la charge négative en x=0 ⇒ pour la pousser en x=1 il faut exercer un travail de :
W = F * x ⇒
W = 1 * 1 = 1J ⇒
EP = W ⇒
EPf - EPi = 1J ⇔
EP(1) - EP(0) = 1J ⇔
EP(1) - 0 = 1J ⇔
EP(1) = 1J ⇒
V(1) = EP(1) / q ⇔
V(1) = 1 / -0,5 = -2J
Analyse :
• le graphe de EP est celui correspondant à plaque négative et charge positive ;
• le graphe de V est le symétrique de celui de la plaque négative ⇔ le champ de potentiels est le même que celui de la plaque négative au signe près.
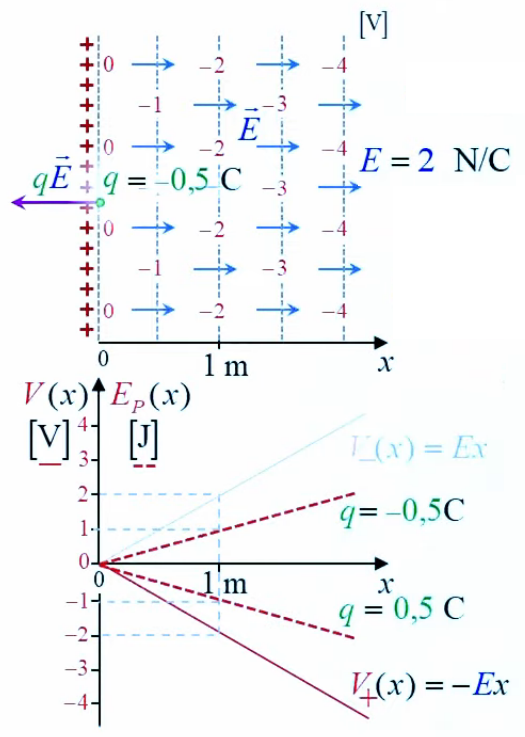
Le signe + de V+(x) signifie qu'il s'agit du potentiel de la plaque positive.
Le graphique suivant résume les quatre cas de figure.
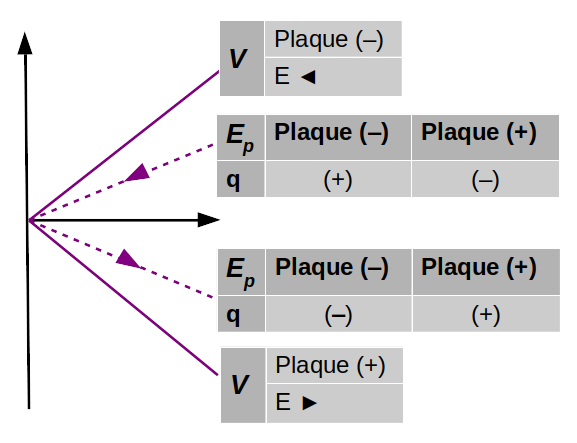
Toute charge (quel que soit son signe) se dirige dans le sens de la diminution de son énergie potentielle. La différence c'est que les charges négatives remontent le potentiel (c-à-d vont contre le champ), tandis que les charges positives descendent le potentiel (c-à-d suivent le champ). La direction du champ indique donc toujours la baisse du potentiel ⇔ lorsqu'on s'éloigne de la plaque, une plaque positive génère donc dans son espace environnant un potentiel qui diminue (dans les valeurs négatives), tandis qu'une plaque négative génère un potentiel qui augmente (dans les valeurs positives).
Accélérateur
de particules
Pour construire (et améliorer) des accélérateurs de particules chargées – utilisés dans certains appareils médicaux, ou encore pour la recherche fondamentale sur la composition de la matière – il est indispensable de connaître la théorie que nous venons de présenter.
Voici comment fonctionne un accélérateur (linéaire). Une source de particules (cube en bleu dans le graphique ci-joint) contient des atomes d'hydrogènes qui sont ionisés (débarrassés de leur unique électron) ⇒ il ne reste de chaque atome H que son unique proton.
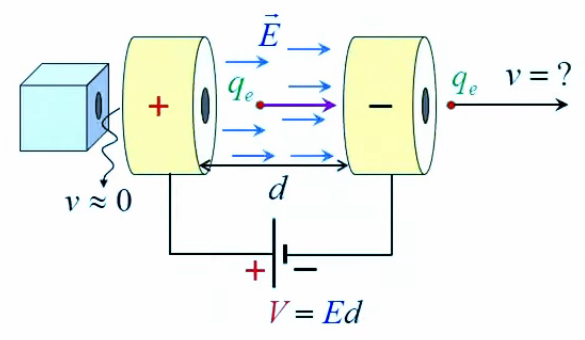
Ces protons sortent de la source à très basse vitesse (v≈0) puis traversent des cylindres de cuivre (qui est conducteur, en jaune dans le graphique). Ceux-ci sont reliés par une source de tension : une différence de potentiel (atteignant des milliers de volts) est créée de sorte que le premier cylindre est chargé positivement et le second négativement (et nous avons vu que le sens du courant va de borne positive à borne négative : #cohesion-electromagnetique). Chaque cylindre fonctionnant comme un plan (cf. supra #methode-gauss-plan), un champ électrique uniforme est ainsi créé entre eux. Ce champ entre les cylindres accélère ainsi les protons qui le traversent.
Application . Comment calculer la vitesse acquise par les protons accélérés ?
Du point de vue de l'ingénieur qui conçoit l'accélérateur, pour dimensionner celui-ci il faut connaître la vitesse en fonction de la tension que l'on va appliquer.
Un façon de résoudre ce problème est de calculer l'accélération : un proton a une certaine masse, or toute masse qui subit une force est accélérée ⇒ on peut donc utiliser les équations du MRUA (cf. supra #cinematique). Cependant une solution plus simple (requérant moins de calculs) consiste à utiliser le principe de conservation de l'énergie, et donc en l'occurrence d'utiliser la notion de potentiel électrique. Nous avons vu qu'à la distance entre ces deux cylindres correspond une différence de potentiel, que l'on peut calculer par V = E * d (256).
Supposons un proton situé contre le second cylindre, et que l'on ramène au premier. Pour contrer le champ il faut exercer un travail, qui confère au proton une énergie potentielle : EP = q * V (254) ... où q et V sont connus ⇒ EP aussi.
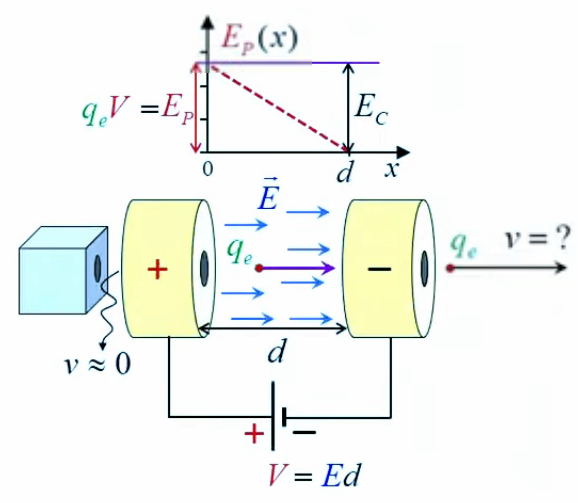
Ensuite si on relâche le proton, alors il repart vers le second cylindre, avec augmentation de son énergie cinétique, jusqu'à atteindre une valeur égale à EP (NB : qui ne diminue pas, cf. infra) ⇒ le calcul de la valeur que v aura alors atteinte se fait en résolvant l'égalité :
EC = EP ⇔
1/2 * m * v2 = q * V ⇔
v = √( q * V * 2 / m)
où :
• la charge q du proton, est la même que celle de l'électron au signe près (cf. supra #atomes) ;
• la masse m du proton est donnée via le nombre d'Avogadro (191) ;
• on fixe V=50.000V ;
⇒ v = 3 * 106 m/s
c-à-d 3.000 km/s, ou encore 1% de la vitesse de la lumière : à cette vitesse les protons mettraient environ deux secondes pour atteindre la lune !
N.d.A. L'énergie potentielle ne diminue pas entre les deux cylindres, car, comme montré dans le graphique ci-joint, le système de l'accélérateur est une combinaison de deux des quatre cas étudiés ci-avant : plaque(+) & charge(+) + plaque(-) & charge(+). Or, par symétrie, les deux effets se neutralisent, l'un correspond à une augmentation d'énergie potentielle tandis que l'autre correspond à une diminution de même ampleur).
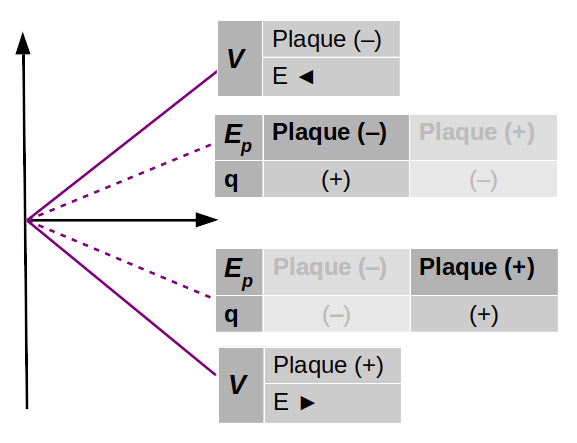
Ainsi en ajoutant des étages d'accélération (c-à-d des couples de cylindres) on peut atteindre des vitesses proches de celle de la lumière. On atteint ainsi des niveaux d'énergie cinétique considérables qui permettent, en faisant se collisionner des protons, d'étudier leurs débris et partant la composition des particules collisionnées. Les accélérateurs sont utilisés aussi pour l'imagerie médicale (dans ce cas les particules accélérées sont des électrons, générant ainsi des rayons-x) ou encore la protonthérapie (des protons sont accélérés par un accélérateur circulaire appelé "cyclotron").

Dans les années 1820, des scientifiques ont relié au pôle positif d'une pile volta un électroscope à feuillets d'or. On constatait alors que les feuillets s'écartaient. Cet écartement mesure la tension de la pile.
Cependant à cette époque on n'en comprenait pas la raison, à savoir que les électrons de ces feuillets rejoignant la pile, les feuillets portaient alors des charges de même signe (en l'occurrence positif), et par conséquent se repoussaient.

Quelques années plus tard Ampère découvrit qu'en reliant les électrodes de la pile par un fil métallique on constatait que l'aiguille d'une boussole placée à proximité du fil était déviée, ce qui pourrait constituer une mesure du courant passant par le fil. Mais il constata aussi que l'effet de tension observée sur les deux feuillets de l'électroscope disparaissait, ce qui rendait impossible la mesure d'une relation entre l'écart des feuillets et la variation de l'aiguille.
Ohm reproduisit alors cette expérience sous diverses formes, et découvrit que dans le système originel la tension disparaissait en raison d'un défaut de la pile volta : elle est composée d'une résistance interne très importante. Il conçut alors une source de tension avec une faible résistance : un thermocouple. La tension est plus faible mais le système présente l'avantage que la tension ne disparaît pas, ce qui permit à Ohm de mesurer la relation entre celle-ci et le courant généré (mesuré par la déviation de la boussole, et d'ainsi confirmer expérimentalement sa théorie mathématique.
Le sens du courant, c-à-d du débit de charges.
Celle-ci, la loi d'Ohm, décrit une relation de proportionnalité entre la tension (le voltage) V appliquée à un conducteur, et le courant I résultant de cette tension. Le coefficient de proportionnalité R est appelé "résistance électrique" : V = R * I.
Notons qu'à cette époque Ohm et les autres savants ignoraient que le courant mesuré par l'aiguille de la boussole correspondait à un flux de charges, et que la tension mesurée par l'écartement des feuillets correspondait à une différence de potentiel électrique, elle même liée à l'énergie potentielle des charges responsables du courant.
Pour illustrer le développement mathématique de la loi d'Ohm au regard des connaissances actuelles sur les électrons, reprenons le cas de l'accélérateur de particules présenté dans la section précédente. La particule y est accélérée sous l'action d'une force continue. Maintenant si l'on place des obstacles sur la trajectoire de la charge qe, sa trajectoire ne sera plus rectiligne, de sorte que sa vitesse n'est plus accélérée. Cette situation est celle d'une barre métallique, dont on sait que ses atomes sont agencés en réseau cristallin. Dans cette situation qui est celle d'un matériaux conducteurs, les atomes perdent un électron périphérique, qui devient libre, et n'est mobile que par l'agitation thermique. Mais si en outre ces électrons libres sont soumis à un champ électrique, alors ils vont en suivre le courant.
C'est une propriété des matériaux conducteurs que d'être composés notamment d'un grand nombre d'électrons libres (à l'opposé, les isolants n'en contiennent que très peu).
Nous allons maintenant faire une hypothèse pour simplifier le développement mathématique de la loi d'Ohm : l'électron considéré dans l'accélérateur possède une charge ... positive (rappelons-nous que l'attribution de la charge négative aux électrons est une convention et non un fait physique : cf. #cohesion-electromagnetique). Concrètement, on pose ainsi que le mouvement des électrons vers la gauche (dynamique qui complexifie l'exposé) c'est comme des charges positives qui vont vers la droite (cas de l'accélérateur étudié plus haut).
On va modéliser (i) une vitesse constante, qui est la moyenne des vitesses de l'ensemble des électrons de charge +, et (ii) un débit de charges.
On peut faire à nouveau l'analogie avec la force gravitationnelle, où une bille de plomb lâchée dans un tube d'huile, subit une force de friction fluide, ayant pour effet que son accélération est annulée, de sorte que la vitesse est constante. Une bille d'or de même dimension descendrait deux fois plus vite qu'une bille de plomb car sa densité est deux fois plus élevée. Dans ces conditions de frottement, la vitesse est donc proportionnelle à la force subie : v ∝ m * g.
On va ici modéliser le même type de phénomène, mais cette fois pour la force électrique. Par (206) :
v ∝ qe * E ⇒
puisque qe est une constante naturelle :
v ∝ E ⇒
v = μ E
où μ est la mobilité électronique des électrons libres du matériaux considéré.
D'autre par le débit de charge (le courant) se mesure par :
I = qe * η * Volume / Δt
où η est la densité des électrons libres par unité de volume du matériaux considéré (⇔ les matériaux isolants, c-à-d peu conducteurs, ont un η de très faible valeur) ⇔ par (162) :
I = qe * η * ( v * Δt * S ) / Δt
où S est la surface de section de la barre de matériaux ⇔
I = qe * η * v * S ⇔ par (258) :
I = qe * η * μ E * S
or : V = E * L (256) ⇔ E = V / L ⇒
I = qe * η * μ * S / L * V ⇔
I = σ * S / L * V
où :
• σ = qe * η * μ
sont trois propriétés physiques propres au matériaux, déterminant sa conductivité électrique (σ) ;
• alors que S / L sont des propriétés géométriques propres à la barre constituée du matériaux ;
⇔
V = 1 / σ * L / S * I ⇔
loi d'Ohm : V = R * I
où
R = 1 / σ * L / S est la résistance du matériaux utilisé.
CQFD
- On notera la cohérence intuitive de la relation physique de R avec la conductivité σ, la surface S de la section : "plus le tuyau est large plus ça passe". N.d.A. : concernant l'effet de L sur R, peut-on dire que le plus la barre est longue dans l'espace, plus sa résistance est longue dans le temps ?
- Ohm avait compris que R = ? * L / S. Ce n'est que plus tard, grâce à la compréhension des composants microscopiques de l'électricité (les électrons), que l'on a pu établir que ?=1/σ.
Une lecture peut être plus intuitive de la loi d'Ohm est I = V / R :
• il ne peut y avoir de courant sans différence de potentiel ;
• le courant est d'autant plus élevé que la résistance est faible.
Ce qui est moins intuitif c'est que dans le vide (on retire la barre) la résistance n'est pas nulle mais ... infinie ! En effet si ∄ barre ⇒ ∄ électrons libres ⇔ η=0 ⇒ par (260) : σ=0 ⇒ par (261) : R=∞.
Revenons à la forme classique de la loi d'Ohm V = R * I , qui est celle la plus utilisée dans la pratique : la connaissance du courant I et de la résistance R du matériaux imposent une tension électrique V=R*I aux bornes du conducteur.
L'effet de la longueur de la barre sur la tension apparaît au travers de R = 1 / σ * L / S (262) : plus la barre est longue ⇒ plus la résistance R est élevée ⇒ plus le potentiel doit être élevé pour fournir un courant déterminé.
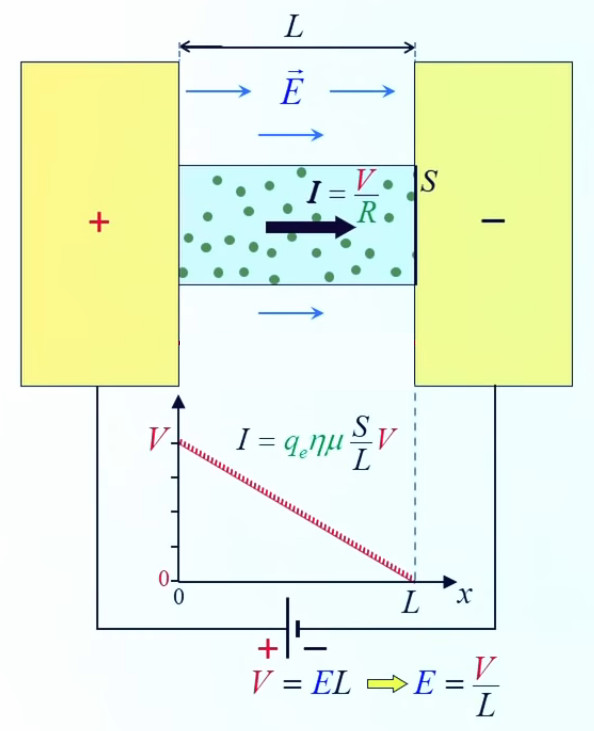
Accélérateur de particules
Un corrolaire de cette propriété est que le potentiel (la tension) diminue progressivement le long du conducteur : plus l'électron est situé vers la droite, plus la distance qui le sépare de la borne négative est petite. Cela est illustré par le graphe de la pente du potentiel (en rouge). C'est la notion de distribution de la tension électrique : la tension n'est pas seulement une valeur donnée pour une pile électrique, c'est aussi une valeur qui diminue tout au long du conducteur soumis à cette différence de potentielle donnée. Cela correspond bien au fait que la tension électrique représente le potentiel électrique c-à-d l'énergie potentielle divisée par la charge (254). Dans l'analogie avec la gravitation, la particule est alors vue comme une masse descendant le long de cette pente.
Et pourquoi la résistance R varie-t-elle dans le même sens que la longueur L de la barre ? La réponse est donnée par V = E * L (256) : si pour un potentiel donné, la distance entre les deux bornes diminue ⇒ le champ, c-à-d la pente du potentiel, augmente nécessairement ⇒ les charges la descendront d'autant plus vite. À priori on aurait pu penser que l'effet de L sur R était de même type de celui de S sur R, or ce n'est pas le cas : L, qui semblait être un paramètre géométrique, apparaît plutôt de nature dynamique car L intervient sur la valeur du champ c-à-d des forces qui sont en jeu.
On peut poursuivre l'analyse de la loi d'Ohm sous sa forme détaillée I = qe * η * μ * S / L * V (259). Ainsi par exemple, avec moins de frottements (μ ↑) la masse va accélérer (NB : les frottements sont causés par les obstacles que constituent les atomes de la barre).
Notons enfin qu'Ohm fut très influencé par la loi de Fourrier sur la conduction de la chaleur ΔT = R * H où
• ΔT est le différentiel de température entre deux "sources de température" (tout comme V est la différence de potentiel) ;
• H est le débit de chaleur entre ces deux sources, au travers d'un matériaux ;
• R est la résistance thermique de ce matériaux.
Ainsi par des développement mathématiques Fourrier avait également démontré théoriquement une relation linéaire entre ΔT et L.
N.d.A. Le schéma suivant illustre un circuit électronique de base, constitué d'une source de potentiel v, générant un courant i, freiné par une résistance R (que l'on peut comparer aux forces de friction de la mécanique). Tout matériaux étant caractérisé par une résistance, correspond ainsi à ce phénomène un composant électronique, parfois appelé "dipôle résistant", et qui fait sens dans la mesure où la résistance de son matériaux diffère de celle du reste du circuit.
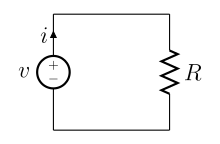
Nous avons jusqu'ici supposé le cas de champ uniformes, c-à-d notamment que les vecteurs du champ ont même direction et module. Il en résulte que les trajectoires des électrons dans ce champ sont également uniformes, ce qui facilite grandement leur calcul. Mais lorsque le champ est quelconque, les trajectoires des électrons sont généralement non rectilignes. Une technique de calcul de ces trajectoires est l'intégrale de circulation.
Trajectoire
Pour développer tout cela il nous faut commencer par montrer qu'une différence de potentiel est indépendante de la trajectoire suivie par un corps pour passer d'un niveau de potentiel à l'autre.
Nous allons donc montrer qu'il y a là une analogie directe avec le champ gravitationnel : dans la section #potentiel-gravitationnel nous avions en effet montré que le travail à fournir pour élever une masse m à une hauteur h est indépendant de l'angle que fait avec le sol la pente par laquelle la masse est élevée, c-à-d indépendant de la longueur du chemin choisi.
Le schéma ci-dessous illustre la trajectoire quelconque d'un corps entre les positions initiale (i) et finale (f), auxquelles correspondent une différence de potentiel ΔV. Au corpuscule sont associés un vecteur déplacement dl→ et le champ E→.
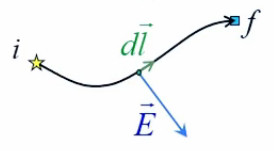
Commençons par le cas d'un champ uniforme tel que E = 1 N/C et ΔV = 1 J/C ⇒ par (257) dl = 1. Si l'on déplace alors la charge d'un niveau de potentiel x à x+1 selon un trajectoire qui n'est plus parallèle au champ ⇒ dl augmente. On se rend alors compte qu'il faut adapter ΔV = E * Δl (257) pour que la modélisation mathématique soit cohérente avec le fait que le champ de potentiels est une "lasagne" indépendante de la trajectoire prise pour passer d'un niveau de potentiel à l'autre. En fait ΔV = E * Δl= F / q * Δl = W / q n'est qu'un cas particulier tel que le vecteur "force" F→ et le vecteur "déplacement" Δl→ sont parallèles. Or on sait que la formulation générale du travail, c-à-d pour une forcée exercée dans une direction quelconque par rapport à celle du déplacement, est donnée par le produit scalaire du vecteur force et du vecteur déplacement du point d’application de la force (cf. supra #produit-scalaire).
Pour montrer cela dans une autre expérience, plaçons-nous à nouveau d'abord dans le contexte gravitationnel. Un homme placé sur un plateau roulant dans un MRU (cf. supra #cinematique) soulève une masse. La trajectoire de celle-ci ne sera donc plus perpendiculaire au sol.
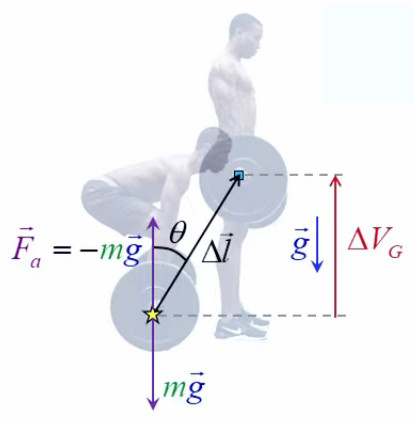
Or le travail effectué par l'homme est inchangé par rapport à la situation de repos : son mouvement implique certes une énergie cinétique, mais celle-ci étant constante durant l'exercice (puisqu'on est en MRU), le bilan énergétique (notion de différentiel) est identique à la situation sans mouvement. C'est donc la projection verticale du déplacement (c-à-d sur la direction de la force gravitationnelle) qu'il faut prendre en compte dans le calcul du travail. Nous avons vu que c'est précisément ce que fait le #produit-scalaire :
W = F→a . Δl→ = m * g * Δl * cos(θ) ⇔
W = - m * g→ . Δl→ ⇒ en vertu du principe de conservation de l'énergie :
N.B. L'apparition du signe " - ", est due au remplacement de g par g→, et exprime que le travail est calculé à partir de la force appliquée (orientée vers le haut) et non du poids c-à-d la force gravitationnelle (orientée vers le bas). Ce signe - n'implique pas que le travail est négatif : F→a est appliquée vers le haut, ce qui implique que θ<π/2 ⇒ cos(θ)>0 ⇒ W est ici bien positif !
ΔEp = - m * g→ . Δl→ ⇒ par (250) :
ΔVG = - g→ . Δl→
Ainsi la différence de potentielle est bien positive, c-à-d que le potentiel augmente, dans le sens opposé à celui du champ ... et inversement (NB : on retrouve ainsi le résultat exposé dans notre graphe synthétique du chapitre consacré au potentiel électrique).
Champ
équipotentiel
Rien n'empêche d'appliquer au champ électrique les principes développés ci-dessus :
• m devient q
• g devient E
⇒
W = - m * g→ . Δl→
devient
W = - q * E→ . Δl→ ⇒ par (255) :
ΔV = - E→ . Δl→
que l'on comparera utilement à :
ΔV = E * (zf - zi)
(257)
en comprenant la signification du signe - lorsque l'on passe de la norme E au vecteur -E→.
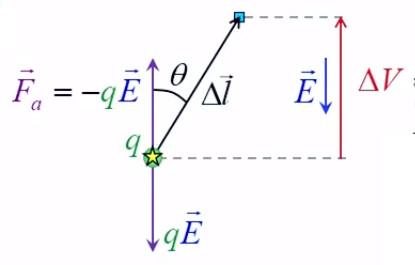
Or, par définition du produit scalaire, dans (263), Δl→ représente des vecteurs qui ont tous la même projection Δz sur E→ :
ΔV = E * Δz
N.B. il s'agit ici non plus de vecteurs mais de scalaires, d'où la disparition du signe " - ".
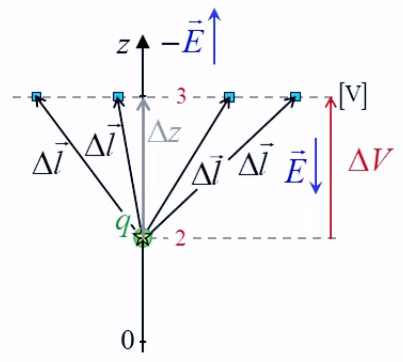
On a ainsi démontré la cohérence de la notion de champ équipotentiel : quelle que soit l'inclinaison, c-à-d la direction suivie pour passer d'un potentiel au suivant, la différence de potentiel est identique !
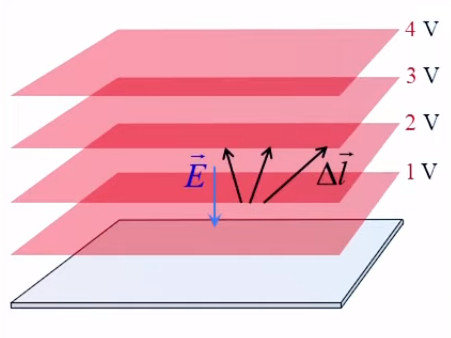
Et comme chacune de ces trajectoires rectilignes peut être vue comme la somme d'une multitudes de trajectoires également rectilignes mais non parallèles, il en résulte que le principe demeure dans le cas de trajectoires quelconques c-à-d non rectilignes :
∑n=1N ΔVn = - ∑n=1N E→ . Δln→ ⇔
ΔV = - E→ . ∑n=1N Δln→ ⇔
ΔV = - E→ . Δl→ = E * Δz
c-à-d (263).
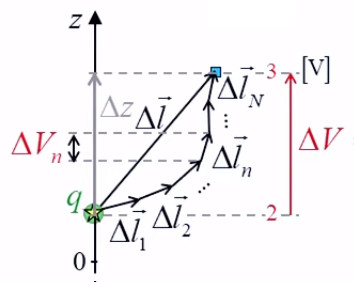
Pour généraliser au cas de courbes quelconques lisses il suffit, dans (264) de remplacer les Δln→ par des dl→ arbitrairement petits, puis de les intégrer (sommation "continue", c-à-d comportant un nombre infini de termes) :
∫ dV = - ∫ E→ . dl→ ⇔
- La disparition des indices de (264) se justifie par la nature indénombrable des termes d'une somme continue.
- Le membre de droite est appelé "intégrale curviligne" (car elle intègre des distances infinitésimales), et plus précisément "intégrale de circulation" (du champ E→) en raison du produit scalaire entre le champ et les distances infinitésimales.
∫ dV = - E→ . ∫ dl→ ⇔
et par addition vectorielle (cf. #vecteur-addition-multiplication) :
ΔV = - E→ . Δl→
⇔ on retrouve à nouveau (263).
Champ
quelconque
Nous venons de montrer que le principe de champ de potentiel uniforme (plus exactement "champ équipotentiel") est indépendant du chemin suivi entre niveaux de potentiel.
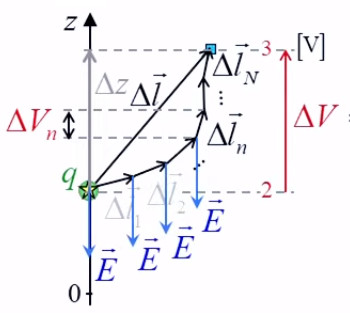
Mais nous avons raisonné dans le cadre d'un champ électrique uniforme. Cette hypothèse de champ constant a permis le passage de (265) à (266) en isolant le champ E→ hors de l'intégrale de circulation. Mais si on lève l'hypothèse de champ uniforme (c-à-d constant), cela ne sera plus possible ...
Ainsi si le champ n'est plus uniforme, alors
∑n=1N ΔVn = - ∑n=1N E→ . Δln→ (264)
devient :
∑n=1N ΔVn = - ∑n=1N E→n . Δln→
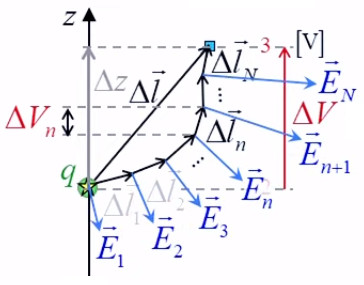
Le graphique suivant illustre des vecteurs de modules et directions différents, ce qui requiert de les distinguer par un indice : E→n ne peut donc plus être extrait de la somme,
et
ΔV = ∫ dV = - ∫ E→ . dl→ (265)
devient :
ΔV = - ∫i→f E→(x→) . dl→ t242
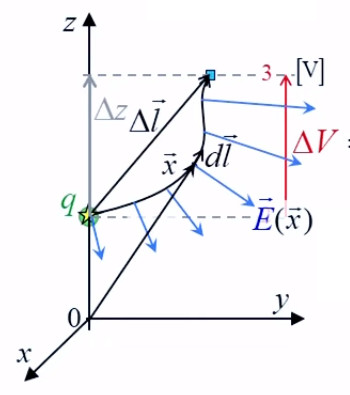
L'égalité (267) ci-dessus indique bien que le champ varie de façon continue de position en position ⇔ on introduit le vecteur position x→ dans un repère cartésien ⇔ on intègre une fonction des coordonnées de l'espace (PS : on devrait également remplacer dl→ par dl→(x→) puisque les vecteurs changent de direction selon leur position, mais les mathématiciens ont pour habitude de ne pas le mentionner). L'égalité ΔV = - E→ . Δl→ = E * Δz n'a donc plus de sens dans le cas d'un champ non uniforme.
On doit alors en déduire que l'équipotentialité n'est plus localisée sous la forme de plans, mais de surfaces qui sont d'autant plus complexes que le champ électrique est complexe. Lorsque nous étudierons le calcul du potentiel d'une charge ponctuelle (notion de "champ coulombien") génèrant un champ non uniforme, nous verrons que demeure néanmoins la propriété d'indifférence du différentiel de potentiel par rapport au chemin suivi entre niveaux de potentiel, c-à-d entre surfaces équipotentielles complexes (on dit que le champ électrique est "conservatif").
Pour comprendre intuitivement (267), il est utile de l'interpréter en terme d'énergie potentielle (rappel : VE = EP / q (254) ). Celle-ci est calculée par le travail réalisé pour passer du point i au point f (travail de la force "appliquée") :
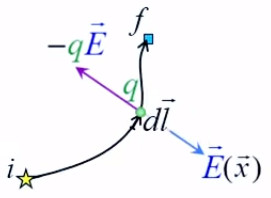
dW = - q * E→ . dl→ ⇒
W = ∫i→f dW = ∫i→f - q * E→ . dl→ ⇒
ΔEP = ∫i→f - q * E→ . dl→ ⇒
ΔV = - ∫i→f E→ . dl→ ⇒
qui est bien (267). Rappelons encore une fois que le signe - exprime le fait que le travail réalisé est celui de la force appliquée contre celle du champ (et la différence de potentiel peut être positive ou négative selon la situation).
Les unités du membre de droite sont :
N / C * m = V ⇔
N / C = V / m
qui est l'unité la plus fréquemment utilisée du champ électrique.
Application. Une pile est caractérisée par une différence de potentiel, c-à-d une tension, qui est créée par une réaction électrochimique accumulant des charges négatives sur un pôle et des charges négatives sur l'autre. Il en résulte un champ électrique (dit "dipolaire") sortant du pôle positif et revenant au pôle négatif. Ainsi une pile de 1,5V est telle que l'intégrale du champ - E→ depuis le pôle négatif jusqu'au pôle positif, selon une trajectoire quelconque vaut 1,5V. NB : on notera dans l'image ci-jointe que le champ -E→ remonte bien du pôle négatif (bas) vers le pôle positif (haut).
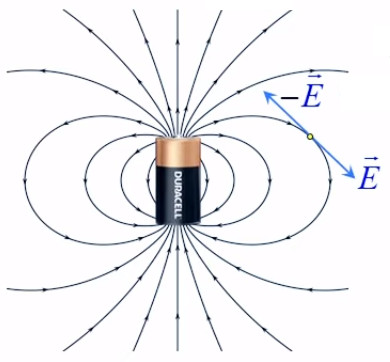
Potentiel coulombien
Lagrange avait introduit la notion de potentiel gravitationnel (253), pour les calculs de mécanique céleste, comme par exemple celui de l'orbite lunaire autour de la Terre. L'intérêt de la notion de potentiel est d'exprimer très simplement le principe de conservation de l'énergie, et d'ainsi simplifier les calculs.
Or Coulomb avait découvert entre-temps la loi du champ de force électrique. Laplace avait alors remarqué l'équivalence – au niveau de la radialité (1→r) et de la dépendance en 1/r2 – entre l'expression des champs gravitationnel et électrique :
- champ gravitationnel : g→ = - G * M / r 2 * 1→r (252)
- champ électrique : E→ = q / ( 4 * π * ε0 * r 2 ) * 1r→ (220)
où la constante gravitationnelle -M * G correspond à q / ( 4 * π * ε0 ).
⇒ Laplace a étendu cette équivalence à la notion de potentiel :
- gravitationnel : ΔVG = - ∫i→f g→ . dl→
- électrique : ΔV = - ∫i→f E→ . dl→ (267)
Le terme "potentiel coulombien" désigne la distribution spatiale de potentiel, associée au "champ coulombien" d’une charge électrique ponctuelle.
Pour calculer l'intégrale de circulation (267) (entre les points x→i et x→f) il faut y injecter (220), où :
- E→(x→) est le champ au vecteur position x→, dans un repère dont l'origine est centrée sur la charge q (idem pour x→i et x→f) ;
- r est la distance entre la charge q et le point de calcul (x→) du champ correspondant à cette charge ; aussi appelée "coordonnée radiale", elle est mesurée relativement au vecteur unitaire radial 1r→.
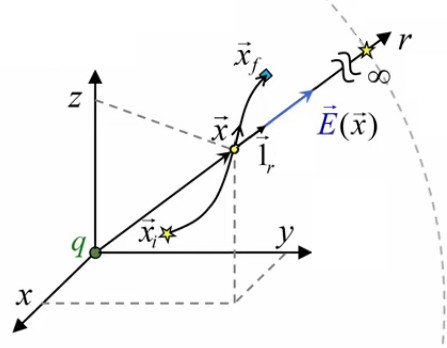
Potentiel
absolu
On pourra alors calculer la distribution de potentiel (ou encore "fonction potentiel") V(x→). Celle-ci est telle que :
ΔV = - ∫x→i→x→f E→ . dl→ = V(x→f) - V(x→i) ⇒
si l'on suppose que le référentiel de potentiel zéro est tel que :
V( x→i ) = 0 ⇒
ΔV = - ∫x→i→x→f E→ . dl→ = V(x→f)
que l'on appelle "potentiel absolu".
Mais ce que l'on cherche c'est le potentiel en x→ et non pas en x→f ⇒
ΔV = - ∫x→i→x→ E→ . dl→ = V(x→)
Il reste à situer le référentiel de potentiel nul de façon pertinente pour calculer le potentiel de la charge q. Serait-il pertinent de le fixer sur la charge elle-même, à l'instar de ce qu'on avait avec la plaque chargée (cf. #potentiel-resistance-electrique) ? Non, ici ce n'est pas la bonne solution car alors r=0 ⇒ E(0)=∞ par (220). On va plutôt, dans la continuité de l'analogie avec la force de gravitation, faire le même choix que pour calculer le potentiel gravitationnel (cf. supra #gravitation-universelle), à savoir l'infini ⇒ E(∞)=0 : ce référentiel est idéal car un charge d'essai située à l'infini ne subit aucune force.
Tous les points situés sur la sphère de l'infini sont donc à un potentiel nul. Notre équation devient alors :
ΔV = - ∫∞→x→ E→ . dl→ = V(x→)
On va commencer par faire ce calcul (passer de l'infini à x→, par succession de petits pas dl→ ) sur l'axe de coordonnée radiale (après on étudiera le cas d'une trajectoire quelconque). Pour ce faire on considère :
• un point courant x'→, de coordonnée radiale r', et circulant de l'infini au point x→ ;
• E→ et dl→ en ce même point courant x'→ ;
⇒ on substitue (220) dans (268) ⇒
ΔV = - ∫∞→x→ q / ( 4 * π * ε0 * r' 2 ) * 1r→ . dl→ = V(x→)
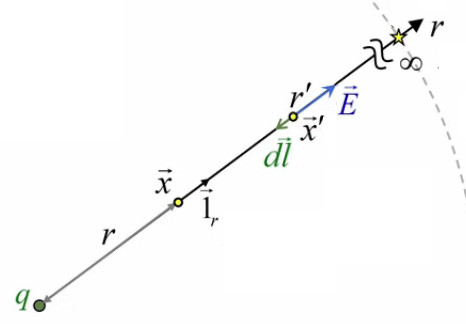
Reste à traiter l'autre facteur de (268), dl→ , qui est tel que :
dl→ = dr' * 1r→
où dr'<0 puisqu'on se dirige de l'infini vers x→ ⇒
ΔV = - ∫∞→x→ q / ( 4 * π * ε0 * r' 2 ) * 1r→ . dr' * 1r→ ⇔
ΔV = - ∫∞→x→ q / ( 4 * π * ε0 * r' 2 ) * dr' * 1r→ . 1r→ ⇔
ΔV = - ∫∞r q / ( 4 * π * ε0 * r'2 ) * dr' ⇔
NB : la valeur de la borne inférieure de l'intégrale est supérieure à la valeur de la borne supérieure, ce qui est cohérent avec le fait que les dr' sont négatifs (on ne doit donc pas mettre de signe "-" devant dr' : cela est implicite dans le calcul de l'intégrale, qui a toujours un sens, de la borne inférieure vers la borne supérieure).
ΔV = - q / ( 4 * π * ε0 ) * ∫∞r 1 / r'2 * dr' ⇒
en remplaçant r' par x pour simplifier la notation ⇒
ΔV = - q / ( 4 * π * ε0 ) * ∫∞r 1 / x2 * dx ⇒ (cf. #integrale)
ΔV = q / ( 4 * π * ε0 ) * [ 1 / x ]∞r ⇔
ΔV = V(x→) = q / ( 4 * π * ε0 ) / r
On notera que cette équation du potentiel coulombien est proche de celle du champ coulombien E→(x→) = q / ( 4 * π * ε0 * r 2 ) * 1r→
(220)
... avec cependant deux différences importantes :
• le champ est vectoriel tandis que le potentiel est scalaire ;
• le champ est dépendant en 1/r2 tandis que le potentiel est dépendant en 1/r.
Soulignons le fait que la formule du potentiel est bien celle d'une distribution : x→ est quelconque : l'ensemble des points situés à une distance r de la charge q constitue une sphère équipotentielle (N.d.A. : on pourrait la comparer à un oignon dont chaque couche de pelure représente un niveau de potentiel).
Interprétation
physique
Pour illustrer la signification physique de cette notion de potentiel, calculons le travail nécessaire pour amener une charge d'essai q0 depuis l'infini jusqu'à la distance r correspondant au point x→ : pour ce faire je dois combattre la force électrique qui vaut q0 * E→ ⇒ on obtient la valeur de ce travail en multipliant (268) par q0 ⇒
- ∫∞→x→ q0 * E→ . dl→ = q0 * V(x→)
où l'on voit que le potentiel c'est ce travail (c-à-d l'énergie) divisé par la charge d'essai q0.
Généralisons enfin ce résultat au cas d'un trajet quelconque, et non plus seulement le long d'un axe radial (sans quoi la notion de potentiel n'aurait pas grande utilité). Que se passe-t-il lorsqu'on passe d'une charge d'essai de l'infini au point x→ ? Dans ce cas les dl→ ne sont plus alignés sur l'axe radial : ils sont quelconques.
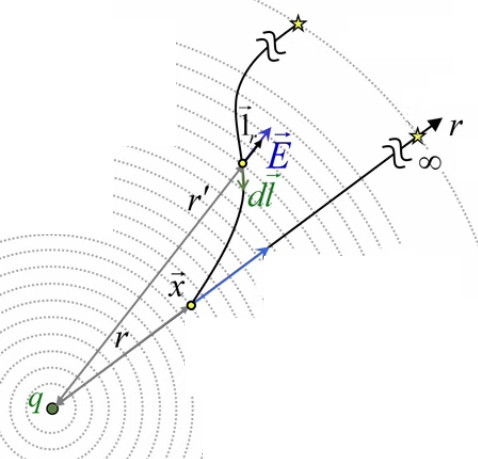
Le champ situé à une distance r' de la charge q se calcule par E→(x→) = q / ( 4 * π * ε0 * r' 2 ) * 1r→ (220). Quant aux dl→, on a pas besoin de les calculer car ils apparaissent au travers du produit scalaire de ΔV = - ∫∞→x→ E→ . dl→ = V(x→) (268).
Or celui-ci est tel que :
E→ . dl→ = q / ( 4 * π * ε0 * r' 2 ) * 1r→ . dl→
or par (58), on sait que le produit scalaire de deux vecteur est la projection de l'un sur l'autre ; or en l'occurrence dr' est la composante radiale de dl→ :
1r→ . dl→ = dr' ⇒
E→ . dl→ = q / ( 4 * π * ε0 * r' 2 ) * dr' ⇒
qui correspond bien à (269) ⇔ un déplacement quelconque (et donc l'intégrale de circulation correspondante) est équivalent à un déplacement radial.
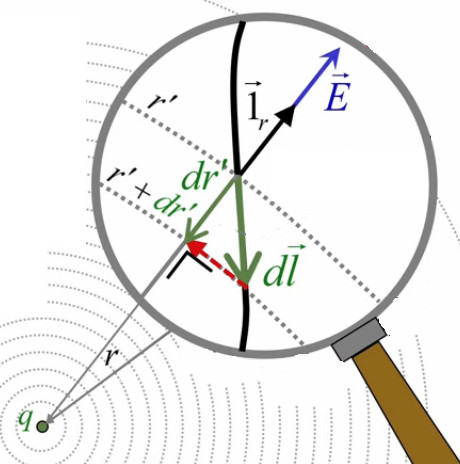
Cela est illustré par le schéma suivant, qui montre que tous les vecteurs dl→ des deux trajectoires quelconques de i à f ont la même composante radiale. Autrement dit, le travail effectué pour amener la charge de i en f est indépendant du chemin suivi.
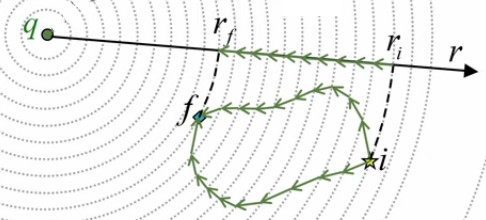
Et de même, dans le cas d'une trajectoire circulaire, l'intégrale de circulation du champ électrique est nulle : ∮ E→ . dl = 0 ⇔ si on multiplie les deux membres par une charge d'essai quelconque q0 on voit que le travail total pour déplacer la charge sur un aller-retour est nul : l'énergie utilisée pour aller de i à f sera regagnée lors du trajet retour. Autrement dit, le champ électrique est conservatif. On voit ainsi que le concept de potentiel est notamment utile pour expliquer et formuler le principe de conservation.
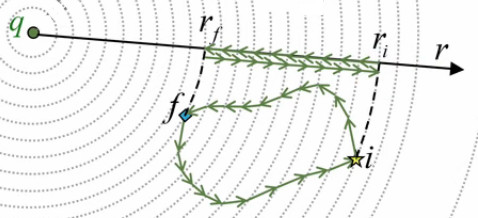
Notation, définition et calcul d'une grandeur physique
- ΔV = - ∫∞→r E→ . dl→ (268) est une définition du potentiel.
- V(r) = q / ( 4 * π * ε0 ) / r (270) est une façon de calculer le potentiel.
- ΔV = V(r) sont les deux notations du potentiel (à une distance r de la charge q générant le champ E→, et tel que V(∞)=0 : cf. notion de potentiel absolu).
Le graphe ci-dessous est celui du potentiel coulombien V(r) = q / ( 4 * π * ε0 ) / r (270), d'une charge d'essai q0 (ici positive), située à une distance r d'une charge q (ici positive) générant un champ électrique (extraverti puisque q>0).
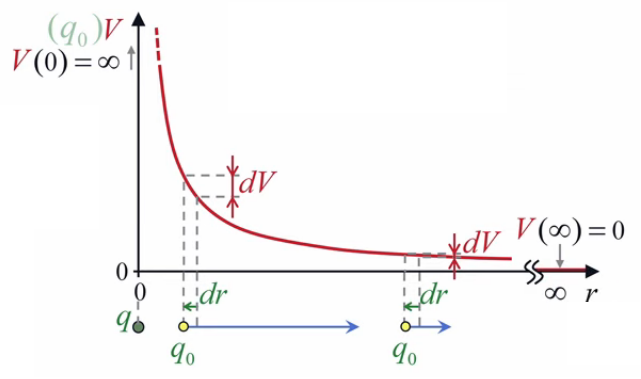
La pente de cette courbe est sa dérivée :
dV / dr = - q / (4 * π * ε0 * r2 )
qui est au, signe près, la composante radiale du champ
E→(x→) = q / ( 4 * π * ε0 * r2 ) * 1r→ (220)
ce qui est logique puisque par définition
V(r) = - ∫∞→r E→ . dl→
(268) ⇔
V(r) = - ∫∞→r E→ . 1r→ * dr ⇔
V(r) = - ∫∞→r E * dr ⇒
V(r) est bien la primitive du champ (avec un signe négatif) E, c-à-d que sa dérivée donne le champ (avec un signe négatif). La pente est bien le module du champ, et elle diminue rapidement avec r car elle diminue en 1/r2 [cf. (271)]. C'est également le cas de la force répulsive (flèches bleues dans le graphe supra) en vertu de :
E→ = F→ / qe (206) ⇔
F→ = E→ * qe ⇔
F→ = qe * q / ( 4 * π * ε0 * r2 ) * 1r→
NB : il s'agit d'une force répulsive dans un champ extraverti (puisque q>0).
dV / dr = - q / (4 * π * ε0 * r2 ) (271) exprime donc un lien différentiel entre le potentiel et le champ, que l'on généralise pour tout potentiel sous la forme dite du "gradient de potentiel" :
∇→ = - E→
qui permet d'obtenir le champ à partir de la connaissance du potentiel.
Charge
négative
Nous avons considéré jusqu'ici le cas de deux charges positives q et q0. Le graphe suivant ajoute le cas de q<0 (partie inférieure), la charge d'essai q0 demeurant positive. Dans cette configuration, le champ généré par q est intraverti puisque q<0, et la force subie par la charge d'essai est attractive puisque q0 et q sont de signes opposés (cf. supra #champ-electrique).
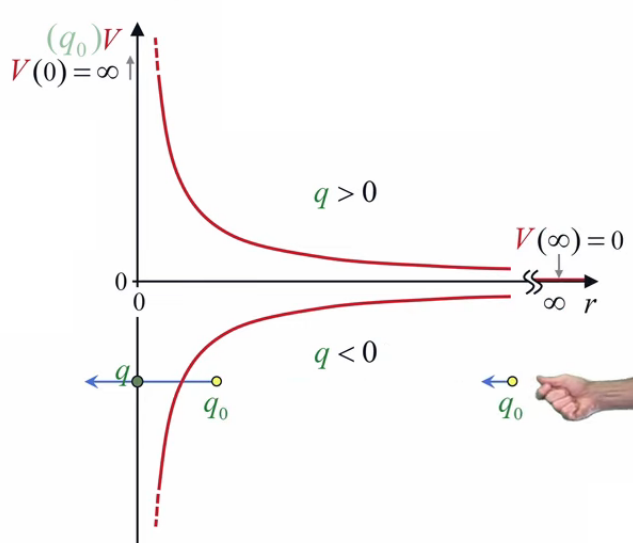
Analyse synthétique dans le cas d'une charge d'essai q0 positive :
- partie supérieure (q > 0) :
force : le champ généré par q est extraverti (puisque q>0), et la force subie par la charge d'essai q0 est répulsive (puisque q0 et q sont de mêmes signes) ;
énergie : la force subie par la charge d'essai q0 étant répulsive ⇒ pour rapprocher q0 de q il faut exercer un travail, ce qui créé de l'énergie potentielle ; et comme l'intensité du champ augmente avec le rapprochement, la force à exercer (et le potentiel ΔV ainsi créé) devient de plus en plus grand au fur et à mesure que q0 est rapprochée de q (notion de "potentiel répulsif").
- dans la partie inférieure (q < 0) :
force : le champ généré par q est intraverti (puisque q<0), et la force subie par la charge d'essai q0 est attractive (puisque q0 et q sont de signes opposés) ;
énergie : la force subie par la charge d'essai q0 étant attractive ⇒ pour éloigner q0 de q il faut exercer un travail, ce qui créé de l'énergie potentielle, et comme l'intensité du champ diminue avec l'éloignement, la force à exercer (et le potentiel ΔV ainsi créé) devient de plus en plus faible (notion de "potentiel attractif").
Interprétons maintenant ces deux configurations au regard du principe de conservation.
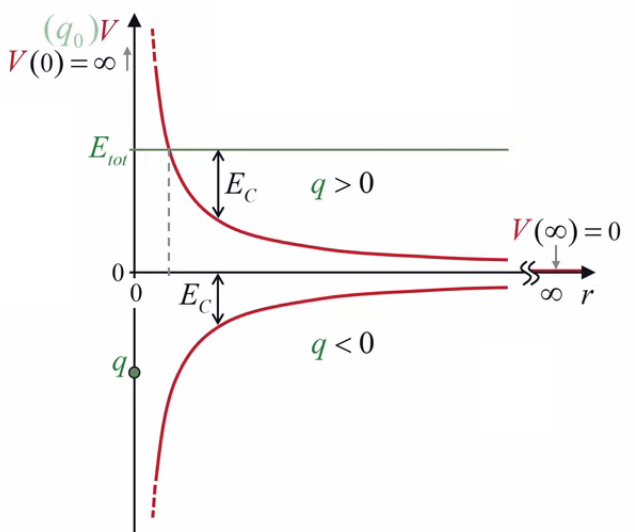
potentiel répulsif : la ligne verticale hachurée en gris correspond à une charge d'essai q0 (>0) dont l'énergie potentielle est relativement élevée : si sa vitesse est nulle (c-à-d si elle est maintenue) alors cette énergie potentielle représente toute son énergie totale ⇒ si cette charge d'essai est lâchée ⇒ elle subit la force de répulsion ⇒ sa vitesse (et donc son énergie cinétique) augmentent, alors que son énergie potentielle diminue d'autant ⇒ à l'infini l'énergie cinétique est égale à la valeur que l'énergie potentielle avait au départ. Notons enfin que plus la charge d'essai est lâchée à une distance éloignée de q, moins grande sera l'énergie cinétique accumulée par q0 à l'infini.
potentiel attractif : considérons maintenant que la charge d'essai q0 (>0) est maintenue (c-à-d que sa vitesse est nulle) à l'infini (vide intersidéral ⇒ son énergie totale est nulle) : si elle est lâchée ⇒ elle est attirée par le champ ⇒ son énergie cinétique augmente vers l'infini ⇔ son énergie potentielle diminue à l'infini (notion de "puits de potentiel").
Physique
atomique
Nous allons étudier maintenant un cas concret, à l'échelle d'un noyau atomique, dont l'ordre de 10-14m (cf. supra #modele-atomique). Nous avons vu que le noyau atomique est composé de protons (charges +) et de neutrons (charges 0), les derniers exerçant un force de cohésion (dite "interaction nucléaire" ou encore "interaction forte") entre les premiers (cf. supra #cohesion-nucleaire). Cette "interaction forte" s'oppose donc aux forces électriques répulsives entre les protons du noyau ⇒ on peut en déduire qu'un noyau contient de l'énergie. Nous allons pouvoir mesurer celle-ci à l'aide de V(r) = q / ( 4 * π * ε0 ) / r (270).
Pour simplifier l'analyse on va considérer le cas d'un noyau contenant seulement deux protons, ce qui est le cas de l'atome d'hélium (He : cf. supra #tableau-periodique).
Atome d'helium.
On pose que la distance qui les sépare est de 10-14m (en réalité c'est un peu moins). Pour créer les atomes d'hélium des étoiles ont du exercer une force (cf. supra #orbites-electroniques) pour abaisser à 10-14m une distance que l'on suppose originellement égale à l'infini. L'énergie requise pour ce faire est donnée par :
VE = EP / q [J/C = V (volt)] (254) ⇔
EP = VE * q
⇒ par (270) :
EP = q2 / ( 4 * π * ε0 ) / r ⇒ par (218) :
EP = q2 * k0 / r ⇒
EP = ( 1,6 10-19 )2 * 9 109 / 10-14 ≈ 2,3 10-14 J
ce qui est un très petite quantité d'énergie ... sauf que la matière est composée d'un très grand nombre de nucléons : 1g de n'importe quelle matière contient 6,02 1023 nucléons (cf. supra #modele-atomique) ⇒ l'énergie contenue dans 1g de n'importe quelle matière vaut :
6,02 1023 * 2,3 10-14 ≈ 14 109 J
ce qui est considérable !
Cette énergie "atomique" est de nature électrique : en libérant les protons de leur force de cohésion induite par le champ coulombien, donc en brisant le noyau (fission nucléaire), on créé de l'énergie cinétique. Comme celle-ci provient de l'énergie potentielle, on peut calculer la vitesse des protons libérés lorsqu'ils arrivent à l'infini :
Ep = m * v2 / 2 ⇔
v = √( 2 * Ep / m ) ⇒ par (193)
v = √( 2 * 2,3 10-14 / 1,67 10 -27 ) ≈ 5,25 106 m/s
La vitesse de la lumière, considérée comme la vitesse maximale physiquement possible, est d'environ 3 108 m/s).
Dans une centrale atomique cette vitesse, c-à-d cette énergie cinétique, à l'échelle microscopique correspond à de l'agitation thermique considérable c-à-d à une forte création de chaleur ⇒ qui chauffe de l'eau ⇒ qui produit de la vapeur ⇒ celle-ci est pressurisée ⇒ conduite vers des turbines ⇒ qui font tourner des alternateurs ⇒ qui produisent de l'électricité.
Mécanique
céleste
Nous avons déjà souligné l'équivalence entre les travaux de Laplace en matière d'électricité et ceux de Lagrange en matière de mécanique céleste. Le tableau suivant synthétise ces équivalences :
| Force électrique | Force gravitationnelle | |
|---|---|---|
| Champ | E→(x→) = q / ( 4 * π * ε0 * r 2 ) * 1r→ (220) | g→ = - G * M / r 2 * 1→r (252) |
| Potentiel | V(x→) = q / ( 4 * π * ε0 * r ) (270) | V(x→) = - G * M * / r (253) |
Ainsi pour calculer la force subie par la Lune dans le champ gravitationnel de la Terre (c-à-d le poids de la Lune dans ce champ), il suffit de multiplier (252) par la masse de la Lune ⇒
m * g→ = - G * M * m / r 2 * 1→r
De même, pour calculer l'énergie potentielle de la Lune il suffit de multiplier (253) par la masse de la Lune ⇒ :
Ep = V * m = - G * M * m / r
où l'on voit par le signe négatif qu'il s'agit d'un potentiel attractif : la Lune est prise dans le puits de potentiel de la Terre.
Faisons maintenant les deux mêmes calculs pour l'atome d'hydrogène, le plus simple des atomes puisqu'il ne comporte qu'un proton et un électron (cf. supra #tableau-periodique). Cet électron joue donc le rôle d'une charge d'essai négative, de sorte qu'il y a attraction vers le noyau (qui génère un champ extraverti puisqu'un proton est de signe +).
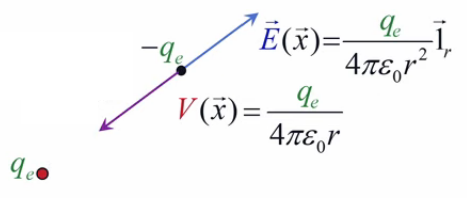
En vertu de E→ = F→ / q0 (206), la force subie par l'électron est donc donnée par :
F→ = - qe * E→(x→) ⇔
F→ = - qe2 / ( 4 * π * ε0 * r 2 ) * 1r→
Et en vertu de VE = EP / qe (254) l'énergie potentielle de l'électron est donnée par :
Ep = V * (- qe ) ⇔
Ep = - qe2 / ( 4 * π * ε0 * r )
où l'on retrouve bien également un potentiel attractif : l'électron est pris dans le puits de potentiel du proton.
C'est le "modèle planétaire de l'atome" que Bohr a élaboré en 1913, en décrivant notamment les propriétés d'émission lumineuse de l'atome. Et en 1925 Schrödinger formule les bases de la mécanique quantique, selon laquelle l'électron ne serait pas une particule mais une onde. Sa célèbre équation, qui comporte le potentiel coulombien, montre qu'un atome génère de la lumière à des fréquences (longueurs d'onde) bien précises. L'expérimentation a montré que l'équation de Schrödinger permet de prédire ces fréquence avec une très grande précision.
Champ et gradient du potentiel
Nous avions vu également qu'il en est de même de la distribution de potentiel : on peut calculer le potentiel en un point quelconque, en fonction du champ qu'il subit. Pour ce faire il suffit de considérer que le point initial du déplacement est située à l'infini ⇒ V(x→) = - ∫∞→x→ E→ . dl→ (268), que l'on appelle "potentiel absolu".
Rappelons que Coulomb avait mesuré le champ électrique expérimentalement. Ensuite, à partir de sa loi expérimentale E→ = q / ( 4 * π * ε0 * r 2 ) * 1r→ (220), il en a déduit la formulation du potentiel en suivant l'idée de Laplace selon laquelle à toute distribution de champ électrique est associée une distribution de potentiels V(x→) = - ∫∞→x→ E→ . dl→ (268), (empruntée à la notion de #potentiel-gravitationnel de Lagrange).
Nous allons ici démontrer la démarche inverse : calculer la valeur du champ en tout point de l'espace à partir du potentiel électrique en ce point. Notons que la voie à suivre pour ce faire n'est pas évidente : le champ étant la variable d'une intégrale, on ne voit pas à priori comme l'en extraire. Pour résoudre ce problème on va recourir à la notion de gradient.
Rappel. Commençons par rappeler l'interprétation physique du potentiel. Soit une charge d'essai q0 ; elle subit la force q0 * E→ ; pour la maintenir en place on doit lui exercer la force - q0 * E→ ; et si l'on veut déplacer la charge le long d'une trajectoire quelconque, il faudra fournir une certaine force exercée sur une distance dl, c-à-d un certain travail (dW).
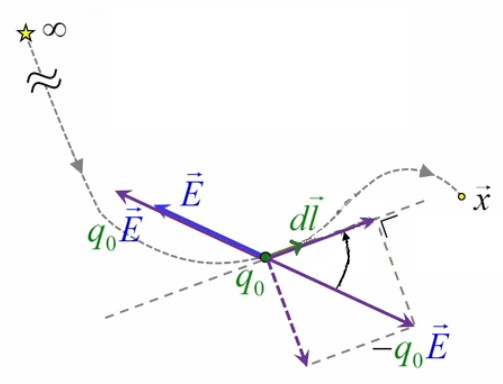
Cette force n'est pas - q0 * E→, mais sa composante tangentielle à la trajectoire (la composante normale à la trajectoire comptant pour rien dans l'effort à fournir) ; cette composante est le produit scalaire - q0 * E→ . dl→ = dW (173).
L'énergie associée à ce travail est évidemment conservée : elle a été transformée en énergie potentielle :
dEp = dW ⇒
dEp / q0 = - q0 * E→ . dl→ / q0 ⇔
dEp / q0 = - E→ . dl→
⇒ par :
V = E / q0 (254) ⇒
dV = - E→ . dl→ (263)
(NB : la différence de potentiel dV correspond au déplacement dl).
qui, substitué dans :
V(x→) = - ∫∞→x→ E→ . dl→ (268) ⇒
vérifie bien que :
V(x→) = ∫∞→x→ dV
Ce rappel étant fait, entrons maintenant dans le vif du sujet. Pour calculer la valeur du champ en tout point de l'espace à partir du potentiel électrique, commençons par constater qu'il n'est pas nécessaire de considérer ici une intégrale de circulation (cf. supra #champ-non-uniforme) : il suffit d'un seul déplacement infinitésimal de la charge d'essai. Or si ce déplacement est infinitésimal, on peut considérer que le champ y est constant.
Dans ces conditions, l'égalité entre les deux membres de droite des deux égalité précédentes :
- ∫∞→x→ E→ . dl→ = ∫∞→x→ dV
se simplifie :
- E→ . dl→ = dV (263)
On va alors exprimer dV en fonction de dl→ en représentant celui-ci dans un repère cartésien, et en l'exprimant en fonction de ses composantes (également infinitésimales) :
dl→ = dx * 1x→ + dy * 1y→ + dz * 1x→ (56).
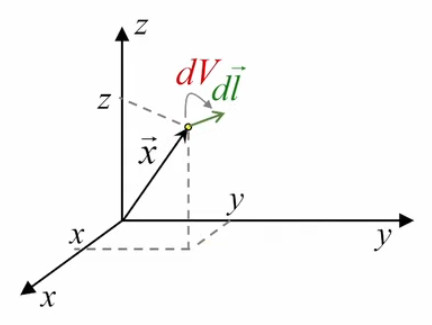
On va alors parcourir dl→ en trois étapes correspondant chacune à un élément de cette somme. Chacun de ces déplacement correspond à celui d'une des trois coordonnées, alors que les deux autres sont inchangées. Autrement dit, chaque déplacement se fait perpendiculairement au plan des deux autres axes de coordonnées.
On peut alors exprimer les variations de potentiel correspondant à chacun de ces déplacements. Le cas exprimé dans la figure ci-contre correspond à la dérivées partielles de V en x : ∂V / ∂x * dx. La variation de V sur l'axe vertical est bien égale au produit de dx par la pente ∂V/∂x en ce point.
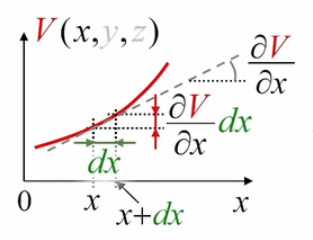
Au bout des trois opérations, la différentielle totale de V vaut alors : dV = ∂V/∂x * dx + ∂V/∂y * dy + ∂V/∂z * dz
On fait alors appel à la notion de gradient : ∇→V = ∂V/∂x * 1x→ + ∂V/∂y * 1y→ + ∂V/∂z * 1z→ (93) ⇒ en comparant les trois dernières égalités on constate que l'une est le produit scalaire des deux autres :
dV = ∇→V . dl→
...que l'on compare alors avec :
- E→ . dl→ = dV (263) ⇒
∇→V . dl→ = - E→ . dl→
Avec cette dernière égalité, nous avons fait pas mal de progrès dans notre tentative de calculer le champ à partir du potentiel. D'une part, connaissant le potentiel, on peut calculer le gradient. D'autre part, on pourrait être tenté de simplifier en supprimant dl→, mais rappelons-nous qu'on ne peut diviser par un vecteur (cf. #proprietes-produit-scalaire) !
Dans le cadre du présent développement, il est utile de montrer ici cette (non) propriété. Nous avons vu que le produit scalaire est le produit de la norme d'un vecteur par la norme de la projection d'un autre vecteur (cf. supra #produit-scalaire). Or Le schéma ci-dessous montre que différents vecteur peuvent avoir la même projection.
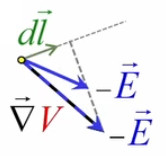
Il en résulte que l'égalité des produits scalaires de deux vecteurs avec un troisième (en l'occurrence dl→) n'implique par que les deux premiers sont nécessairement égaux. Autrement dit, la simplification qui consisterait à supprimer dl→ dans les deux membres de l'égalité ∇→V . dl→ = - E→ . dl→ n'est pas autorisée.
Cependant, dans le cas présent caractérisé par le fait que dl→ est quelconque, cette simplification est autorisée. En effet, puisque dl→ est quelconque, on peut le choisir dans n'importe quelle direction, par exemple uniquement en x :
dl→ = dx . 1x→
(on a donc que dy=dz=0)
or :
- E→ = - Ex . 1x→ - Ey . 1y→ - Ez . 1z→ (56)
∇→V = ∂V/∂x * 1x→ + ∂V/∂y * 1y→ + ∂V/∂z * 1z→ (93)
⇒ par définition du produit scalaire, l'égalité :
∇→V . dl→ = - E→ . dl→
devient :
∂V / ∂x . dx = - Ex . dx ⇔
∂V / ∂x = - Ex
Or on obtient évidemment le même type de résultat si on avait choisi :
dl→ = dy . 1y ⇒
∂V / ∂y = - Ey
Idem pour la composante z.
On constate donc que ∇→V et -E→ ont les mêmes composantes en x,y,z, ce qui signifie évidemment leur égalité :
∇→V = - E→ ⇔
E→ = - ∇→V
Et voilà ! Nous avons ainsi démontré que la connaissance du potentiel V(x,y,z) permet de calculer le champ E→ en tout point.
Nous allons d'abord illustrer le fait que E→ = - ∇→V (274) permet de calculer la valeur du champ en un point, à partir de la fonction de distribution du potentiel (fonction des coordonnées du point de calcul dans l'espace). Il suffit pour cela de calculer le gradient ∇→V = ∂V/∂x * 1x→ + ∂V/∂y * 1y→ + ∂V/∂z * 1z→ (93) , et donc les dérivées partielles qui le constituent (NB : il faut donc que la fonction soit dérivable au point considéré).
Soit la fonction de distribution du potentiel V(x,y,z) = a * x * ( y2 + z2 ) :
∂V / ∂x = a * ( y2 + z2 )
∂V / ∂y = 2 * a * y
∂V / ∂z = 2 * a * z
⇒ à partir de la valeur de a (exprimée en volt/m3) et x,y,z (exprimées en mètres), on calcule facilement ces dérivées partielles ⇒ on connaît les composantes du vecteur gradient :
∇→V = a * ( y2 + z2 ) * 1x→ + 2 * a * y * 1y→ + 2 * a * z * 1z→
... et l'on peut faire cela en tout point.
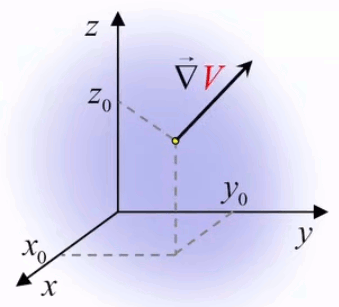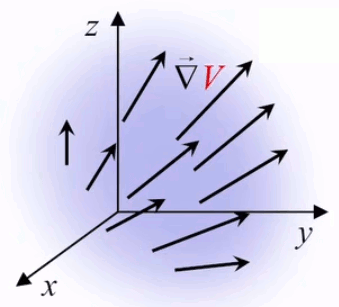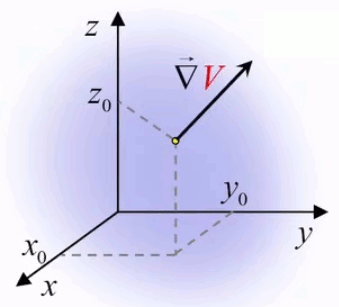
Interprétons maintenant l'illustration de façon qualitative. On suppose la connaissance d'une distribution, représentée dans l'illustration ci-contre par des surfaces équipotentielles vues en coupes (et apparaissant donc comme des lignes).
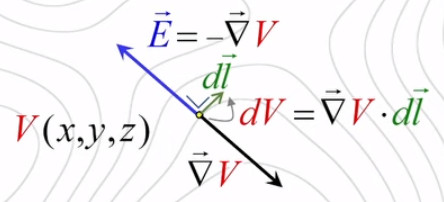
Il résulte de E→ = - ∇→V (274) un lien entre entre champ électrique et ces équipotentielles : le gradient étant perpendiculaire aux surfaces équipotentielles (cf. supra #gradient-lignes-niveau), le champ l'est donc aussi. Par conséquent il résulte de dV = ∇→V . dl→ (273) et de (61) que pour un déplacement dl→ perpendiculaire au champ, alors dV=0 (en effet, si on est perpendiculaire au champ (cf. illustration ci-dessus), on l'est forcément aussi par rapport au gradient puisque celui-ci est opposé au champ). Concrètement, cela veut dire que ce déplacement a lieu le long d'une équipotentielle. Autrement dit, les surfaces équipotentielles sont partout perpendiculaires au champ.
Voir aussi le lien avec la notion de dérivée directionnelle df / dl = ∇→f . 1→l (95).
On est donc maintenant capable d'interpréter, de "lire la carte" de distribution du champ électrique, en observant simplement les équipotentielles :
- orientation : le champ électrique y est perpendiculaire en chaque point ;
- intensité : plus les équipotentielles sont serrées, plus la variation de potentiel est rapide/importante (la pente de potentiel est élevée : pour un dl→ donné on aura un variation de potentiel plus grande dans les zones où les lignes de champs sont plus proches).
Illustrons cette lecture dans un cas simple : le dipôle (deux charges de mêmes valeurs absolues mais de signes opposés). Dans le schéma ci-contre les surfaces équipotentielles (sphériques) sont toujours représentées en coupes (rouges).
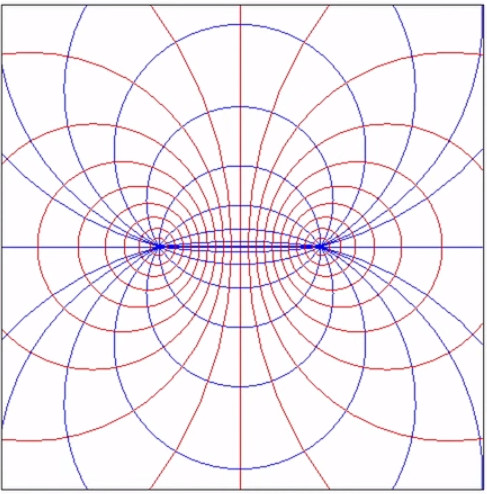
- Orientation : en partant d'un point quelconque de ces équipotentielles, dans une direction perpendiculaire, on dessine les lignes de champ (bleues). Ainsi à chaque perpendiculaire à une équipotentielle correspond une tangente à une ligne de champ. ;
- Intensité :
- rouge : la taille des cercles augmente au fur et à mesure que l'on s'éloigne des charges ;
- bleu : plus les lignes de champ sont espacées plus le champ est faible.
La où les lignes de champ sont serrées (ce qui indique un champ important), on a aussi des équipotentielles serrées indiquant la direction de plus grande variation de potentiel, le champ allant dans la direction de plus grande variation négative (chute de potentiel) puisque E→ = - ∇→V (274) (le gradient indique la direction de variation positive du potentiel).
Voilà qui illustre clairement que la connaissance de la distribution de potentiel induit la connaissance des lignes de champ.
Passons maintenant à un dernier exemple : le calcul du champ électrique produit par une charge ponctuelle. Pour ce faire faire on va donc partir du potentiel coulombien :
V(x→) = q / ( 4 * π * ε0 ) / r (270)
pour en déduire le champ coulombien :
E→ = q / ( 4 * π * ε0 * r 2 ) * 1r→ (220).
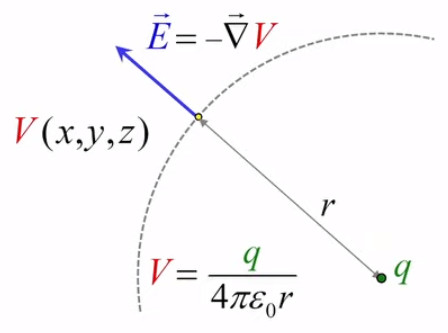
Coupe d'une sphère.
On applique à nouveau E→ = - ∇→V (274) pour calculer le champ à partir du gradient ∇→V = ∂V/∂x * 1x→ + ∂V/∂y * 1y→ + ∂V/∂z * 1z→ (93). Celui-ci se calcule via les dérivées partielles de la fonction V(x,y,z) ⇒ il faut exprimer le rayon r en fonction de ses coordonnées cartésiennes de l'espace. Pour ce faire on va placer le repère cartésien sur la charge elle-même (c-à-d que celle-ci se trouve à l'origine du repère).
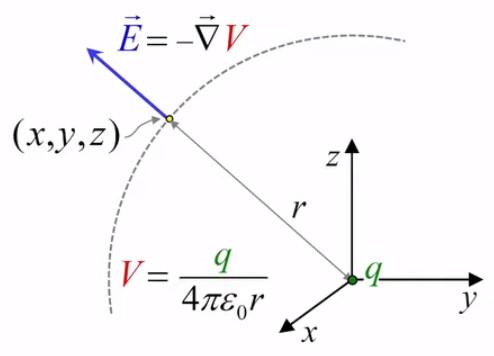
Ainsi, le point (x,y,z), dont on veut calculer le champ, permet d'exprimer r le plus simplement : grâce au théorème de Pythagore (23) on sait que :
r = (x2 + y2 + z2)1/2
⇒
∂V / ∂x = ∂( q / ( 4 * π * ε0 ) / (x2 + y2 + z2)1/2 ) / ∂x ⇒
par ( F[ G(x) ] )' = F'( G(x) ) * G'(x) (88), on calcule facilement que :
∂V / ∂x = q / ( 4 * π * ε0 ) * (-1/2) * (x2 + y2 + z2)-3/2 * 2 * x ⇔
∂V / ∂x = - q / ( 4 * π * ε0 ) * x / (x2 + y2 + z2)3/2 ⇔
∂V / ∂x = - q / ( 4 * π * ε0 * r3 ) * x
et de même :
∂V / ∂y = - q / ( 4 * π * ε0 * r3 ) * y
∂V / ∂z = - q / ( 4 * π * ε0 * r3 ) * z
⇒
∇→V = - q / ( 4 * π * ε0 * r3 ) * ( x * 1x→ + y * 1y→ + z * 1z )
Or x * 1x→ + y * 1y→ + z * 1z (56) est précisément le vecteur position du point de calcul.
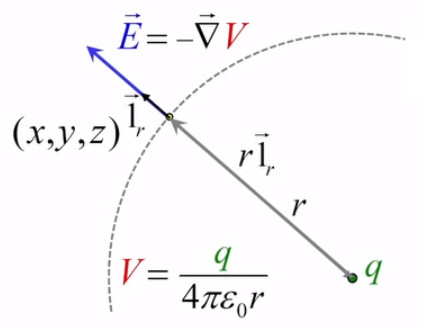
La norme de ce vecteur position étant r, on peut le remplacer par r * 1r→ où 1r→ est le vecteur unitaire radial (204) ⇒
∇→V = - q / ( 4 * π * ε0 * r3 ) * r * 1r→ ⇔
∇→V = - q / ( 4 * π * ε0 * r2 ) * 1r→
qui combiné avec
E→ = - ∇→V (274)
permet de retrouver que :
E→ = q / ( 4 * π * ε0 * r 2 ) * 1r→ (220)
CQFD.
Interprétation. Le vecteur gradient est dirigé vers -1r→ (le vecteur unitaire radial s'éloigne toujours de l'origine, par définition). Le gradient du potentiel pointe dans la direction de croissance du potentiel : le potentiel coulombien varie en effet en 1/r ⇔ plus r est petit, plus le potentiel est grand. Le champ quant à lui est donc dirigé vers les valeurs décroissante du potentiel.
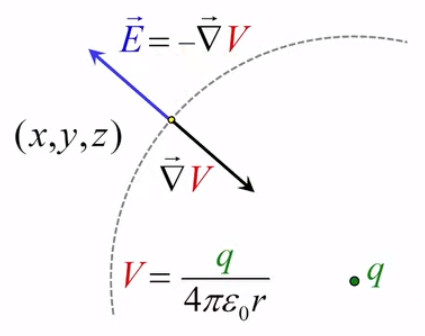
Équations de Poisson et Laplace
Nous allons développer ici les équations de Poisson et Laplace, dans le domaine électrostatique (les équations de Poisson et Laplace sont en fait génériques : elles sont utilisées dans bien d'autres domaines de la physique).
Ces deux équations relient les variables que sont le potentiel électrique V et la densité volumique de charge électrique ρ. L'équation de Laplace est ici un cas particulier de l'équation de Poisson, en l'occurrence l'absence de charge électrique (ce qui est le cas dans le vide) de sorte que ρ = 0 (PS : les travaux de Laplace sont antérieurs à ceux de Poisson, qui généralisera les travaux de Laplace en la matière).
Nous allons voir ici comment Poisson a exprimé la forme locale de la loi de Gauss
∇→ . E→ = 1/ε0 * ρ
(232) ...
où :
• ε0 (constante) est la permittivité du vide (218)
• ρ (variable) est la densité volumique de charge (223)
... en fonction du potentiel électrique V, cela en exploitant E→ = - ∇→V (274).
Le développement est assez simple. Par (232) et (231) (la divergence est la somme des dérivées partielles) :
∇→ . E→ = 1/ε0 * ρ = ∂Ex / ∂x + ∂Ey / ∂y + ∂Ez / ∂z
Or d'une part, (274) et (93) donnent que :
E→ = - ∂V/∂x * 1x→ - ∂V/∂y * 1y→ - ∂V/∂z * 1z→
Et d'autre part, par (56) :
E→ = Ex * 1x→ + Ey * 1y→ + Ez * 1z→
⇒ Ex = - ∂V/∂x ; idem pour y et z
⇒ ∂Ex / ∂x = - ∂2Vx / ∂x2 ; idem pour y et z
⇒ (276) donnne :
∇→ . E→ = 1/ε0 * ρ = - ∂2Vx / ∂x2 - ∂2Vy / ∂y2 - ∂2Vz / ∂z2
soit l'équation de Poisson :
- 1/ε0 * ρ = ∂2Vx / ∂x2 + ∂2Vy / ∂y2 + ∂2Vz / ∂z2
... qui exprime donc la divergence en terme de potentiel.
Opérateur
On aurait développer plus simplement, en faisant appel à la notion d'opérateur, en l'occurrence ∇→ , opérateur différentiel vectoriel. Il s'agit tout simplement de substituer :
E→ = - ∇→V (274)
dans :
∇→ . E→ = 1/ε0 * ρ
(232)
⇒
∇→ . ∇→V = - 1/ε0 * ρ ⇒
Nabla (∇→) étant un opérateur vectoriel, on peut lui appliquer toutes les opérations de l'algèbre vectoriel ⇒
∇→ . ∇→ * V = - 1/ε0 * ρ
N.d.A. Donc, si je comprends bien, cela induit que l'on peut considérer que le gradient de V est équivalent au produit du nabla et de V : ∇→V ≡ ∇→ * V, et que par conséquent ∂v/∂x = ∂/∂x * V... Soit, mais comment intégrer cela avec la définition de la dérivée (81) ?
Occupons-nous alors du produit scalaire de nabla par lui-même, qui par (59) vaut :
∇→ . ∇→ = ∂2 / ∂x2 + ∂2 / ∂y2 + ∂2 / ∂z2
On peut voir le membre de droite de cette égalité comme un opérateur, cette fois scalaire. Par conséquent l'égalité précédant celle-ci-dessus devient :
( ∂2 / ∂x2 + ∂2 / ∂y2 + ∂2 / ∂z2 ) * V = - 1/ε0 * ρ ⇒
( ∂2 * V / ∂x2 + ∂2 * V / ∂y2 + ∂2 * V / ∂z2 ) = - 1/ε0 * ρ ⇒
∂2V / ∂x2 + ∂2V / ∂y2 + ∂2V / ∂z2 = - 1/ε0 * ρ
N.d.A. Ce passage me pose vraiment problème...
soit à nouveau l'équation de Poisson.
Notons que l'opérateur :
∇→ . ∇→ = ∂2 / ∂x2 + ∂2 / ∂y2 + ∂2 / ∂z2
est appelé "laplacien". Il est malheureusement noté Δ, ce qui peut prêter à confusion car il ne doit pas être confondu avec le signe de différentielle.
Idéalement le laplacien pourrait être noté || ∇→|| 2 en vertu de (60), mais cette notation est rejetée par les scientifiques en raison de sa lourdeur.
Le terme "laplacien" se justifie par le cas particulier que Laplace avait posé, soit celui du vide, pour lequel l'équation de Poisson devient :
0 = ∂2Vx / ∂x2 + ∂2Vy / ∂y2 + ∂2Vz / ∂z2 ⇒
l'équation de Laplace :
0 = ΔV
ce qui, si je comprends bien, devrait, étant donné notre système de notation de l'opérateur de multiplication (cf. supra #fractions), être ici noté : 0 = Δ * V, ce qui par ailleurs lève l'ambiguïté par rapport au signe de différentielle (il s'agit bien ici d'un opérateur). Je vais néanmoins appliquer la notation de Clipedia.
La forme courte de l'équation de Poisson est donc :
ΔV = - ρ / ε0
où l'on notera que les unité du laplacien ne sont pas les unités du potentiel, mais 1 sur des longueurs au carré ⇒ les unités permettent d'interpréter le signe Δ.
L'équation de Laplace ΔV = 0 (279) n'est valable que dans le vide. Le graphique ci-contre illustre le cas d'un système de charges discrètes. L'équation de Laplace étant de nature locale, elle s'applique à tout point de cette illustration, à l'exception des zones de distribution de charges (cercles rouge et bleu), pour lesquelles c'est alors l'équation de Poisson ΔV = - ρ / ε0 (280) qui décrit la situation.
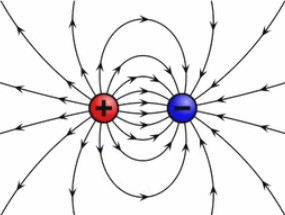
Pour interpréter le sens des flèches, relire #algebre-electricite.
De même c'est l'équation de Poisson qu'il faut appliquer pour calculer la distribution de potentiel, dans l'exemple illustré ci-contre, d'un faisceau de charge positives (protons). En l'occurrence il s'agit donc de calculer les dérivées secondes du potentiel, en fonction de la densité volumique de charge ρ caractérisant cette distribution.
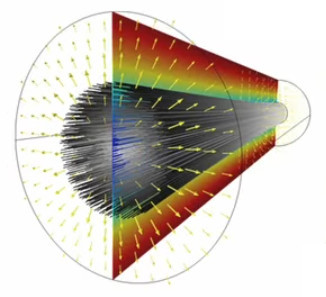
Rappelons la signification géométrique du signe de la dérivée seconde :
- f '' > 0 : la pente est croissante ⇔ en tout point la courbe est au dessus de la tangente en ce point ;
- f '' < 0 : la pente est décroissante ⇔ en tout point la courbe est en dessous de la tangente en ce point ;
- f '' = 0 correspond au point d'inflexion, qui est tel que d'un côté la courbe est supérieur à la tangente en ce point, tandis que de l'autre côté elle est inférieure.
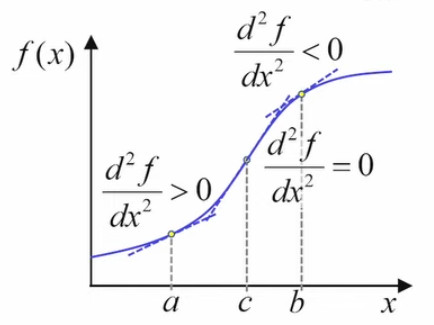
L'interprétation de l'équation de Laplace ∂2Vx / ∂x2 + ∂2Vy / ∂y2 + ∂2Vz / ∂z2 = 0 est un peu plus complexe à interpréter géométriquement : les courbures de variations du potentiel dans les trois directions de l'espace se combinent de telle sorte que la somme des trois dérivées secondes vaut zéro.
Nous allons illustrer cela en reprenant le cas du dipôle, mais en considérant que les charge ponctuelles sont deux cylindres vus en coupe : dans le repère cartésien l'axe Z sort hors du plan XY (cf. la pointe de flèche "⊙" à l'intersection des axes X et Y), et les cylindres sont de longueur infinie.
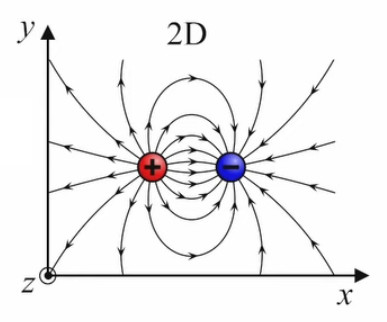
Donc rien ne varie en z ⇒ si la charge ne varie pas en z alors le potentiel non plus ⇒ les dérivées en z sont nulles ⇒ ∂2Vx / ∂x2 + ∂2Vy / ∂y2 = 0. L'interprétation algébrique devient alors plus intuitive : les courbures en x et y sont opposées : si en se déplaçant dans la direction x on a une courbure du potentiel positive, alors la courbure du déplacement en y est nécessairement négative.
L'interprétation géométrique correspondante est illustrée par le graphe ci-dessous de la distribution de potentiel des deux cylindres de charges opposées. On y constate bien qu'en chaque point d'un déplacement le long d'une courbe en x (c-à-d parallèlement à l'axe X) correspond un courbe de signe opposé en y. Là où il n'y a pas de charges, c-à-d dans le vide, on aura toujours cette relation des courbures du potentiel.
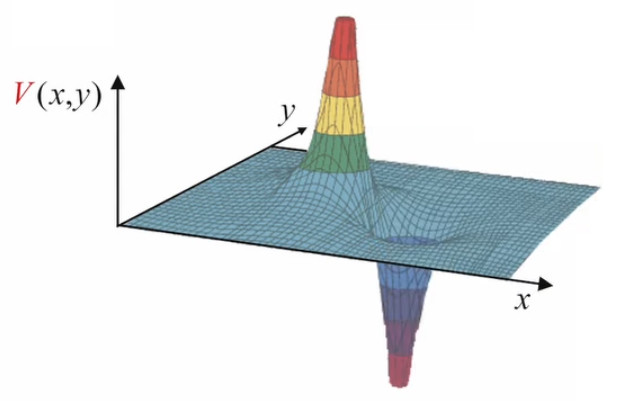
Ci-dessous, un second exemple représentant le graphe d'une fonction V(x,y) = a * x * y. Les dérivées secondes en x et y sont clairement toutes deux nulles. Les courbures ont-elles pour autant disparu, de sorte que le graphe serait plat ? Non, évidemment. Ainsi si l'on se déplace sur la bissectrice x=y on obtient une fonction V(x,y) = a * x2 soit une dépendance parabolique.
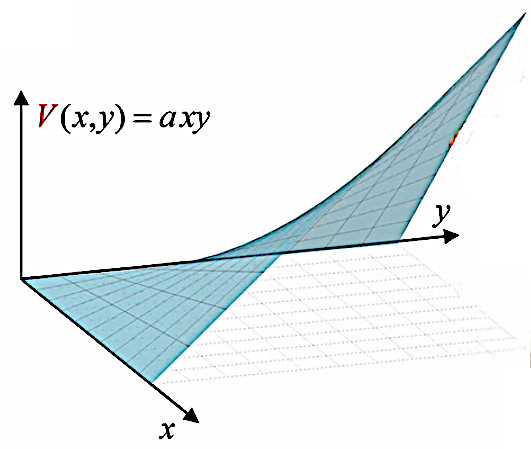
En chaque point de cette bissectrice, sur la surface, on a bien une courbure positive ainsi que, dans la direction orthogonale, une courbure négative. La valeur nulle du Laplacien exprime donc que, dans le vide, toute courbure du potentiel dans une direction est composée par une courbure de signe opposé, dans la direction orthogonale.
Cette surface bleue est dite "doublement réglée" : pour une même valeur d'une des deux variables, l'autre se déplace sur la surface le long d'une droite. Ainsi la pente d'une droite parallèle à l'axe X augmente avec la valeur correspondante de y (considérée comme constante, par rapport aux valeurs de la droite en X), et de même la pente d'une droite parallèle à l'axe Y augmente avec la valeur correspondante de x.
Illustrons maintenant l'équation de Poisson ΔV = - ρ / ε0 (280) par le faisceau de protons évoqué plus haut. Il est caractérisé par une densité volumique de charges électriques (en l'occurrence, positives), soit ρ.
Ce type de faisceau est utilisé notamment dans la "protonthérapie" pour détruire des cellules cancéreuses tout en préservant les cellules environnantes. Le faisceau de proton présente l'avantage d'une précision beaucoup plus grande qu'avec les techniques habituelles des rayons gamma ou X.
Cette précision est cependant limitée. Nous allons le montrer (sommairement) au moyen de l'équation de Poisson, et en supposant que le faisceau de protons est cylindrique. On le décrit dans un repère cartésien, l'axe Z correspondant à celui du déplacement des protons.
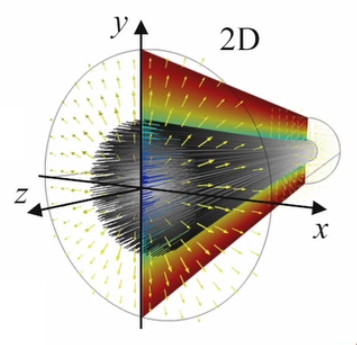
Dans cette condition, si l'on suppose que le faisceau ne s'élargit pas, on peut alors supposer que tout est invariant en z (densité et donc aussi potentiel), de sorte que
∂2Vx / ∂x2 + ∂2Vy / ∂y2 + ∂2Vz / ∂z2 = - ρ / ε0
devient :
∂2Vx / ∂x2 + ∂2Vy / ∂y2 = - ρ / ε0
Cependant dans la réalité le faisceau s'élargit, mais on peut réconcilier la formulation ci-dessus avec la réalité de l'élargissement, par le fait que, en raison de l'extrême étroitesse du cylindre, on peut supposer que les variations en z correspondant à l'élargissement sont très petites relativement aux variations en x et y.
Dans ces conditions on constate que le graphe de ρ(x) est en cloche (mesure le long d'une parallèle à l'axe X), et ses valeurs sont positives (puisqu'il s'agit de protons). Il en est de même pour y étant donné la symétrie du système. Or le membre de droite de (281) étant négatif, il en résulte que c'est également le cas du membre de gauche. Et comme la symétrie du système implique que x et y sont de même signe, il en résulte que ce membre de droite est négatif. La courbure du potentiel est donc négative.
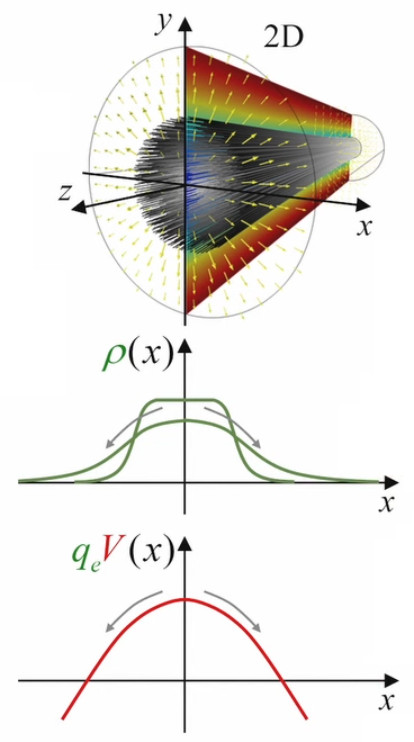
Et en vertu de EP = q * V (254) c'est également le cas de l'énergie potentielle. Par conséquent un proton situé sur l'axe central du cylindre aura une énergie potentielle maximale. Baignant dans cette énergie potentielle à courbure négative et générée par l'ensemble des protons auquel il appartient, son énergie ne peut donc faire que diminuer : un proton situé près de l'axe central aura une tendance naturelle à s'en éloigner. Ce faisant il acquiert de l'énergie cinétique de sorte que le flux des protons dans ce faisceau va s'élargir, et donc aussi la densité de charge. Ce phénomène est appelé "auto-potentiel" : les protons sont pris dans le potentiel qu'ils génèrent eux-mêmes, et s'éloignent donc du centre du faisceau.
C'est pourquoi les systèmes de protonthérapie sont équipés de lentilles magnétiques, qui permettent de focaliser le faisceau, malgré l'élargissement naturel du faisceau causée par le phénomène d'auto-potentiel.
Une explication alternative au développement ci-dessus pourrait reposer sur la distribution du champ électrique, représenté par les flèches jaunes, orientées vers l'extérieur : le champ "tire" les protons vers l'extérieur. Cependant le champ électrique étant une grandeur vectorielle, pour analyser ce genre de phénomène (faisceau de charges), le calcul est beaucoup plus simple s'il porte plutôt sur la grandeur scalaire qu'est le potentiel, et cela au moyen de l'équation de Poisson (l'alternative consistant à construire le champ étant nettement plus complexe).
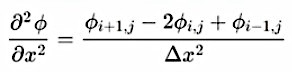
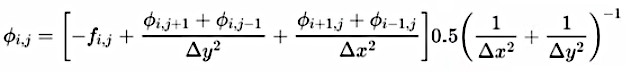
On peut donc mesurer facilement le phénomène d'élargissement du faisceau des protons. Mais l'équation de Poisson peut être appliquée dans d'autres domaines de la physique, sous des formes spécifiques :
- gravitation : ΔΦ = f où :
• Φ : potentiel gravitationnel ;
• f : distribution de masses, proportionnelle à la masse volumique de l'objet étudié ;
⇒ on peut par exemple calculer le potentiel gravitationnel au sein du soleil, et ainsi mieux comprendre le comportement des étoiles. - Physique des fluides : Δp = - div( u . ∇u ) où :
• Δp : laplacien de la distribution de pressions ;
• - div( u . ∇u) : champ de vitesses, c-à-d de la vitesse d'écoulement du fluide.
Ondes gravitationnelles
N.B. Cette section concerne une matière qui ne relève plus de la culture générale, mais de la recherche avancée. Il n'est donc pas attendu du lecteur qu'il comprenne toutes les équations mentionnées.

L'animation ci-contre illustre deux étoiles à neutrons (corps célestes dont la masse volumique est extraordinairement élevée, de l'ordre de mille milliards de tonnes par litre) qui s'étant rapprochées se sont ainsi mises en orbite autour l'une de l'autre. Ces mouvements orbitaux entraînent d'infimes ondulations, dites "ondes gravitationnelles".
La force de gravitation est la force d'attraction exercée l'une sur l'autre par deux masse M et m séparée par une distance r : FN = G * M * m / r 2 (251)
On notera la similitude de cette formule avec FC = kC * q1 * q2 / r 2 (202), décrivant la force électrique entre deux corps chargés électriquement.
Différences. La force électrique est d'un ordre de grandeur nettement plus élevé que la force gravitationnelle : FC / FN = 4,17 * 10 42 [source]. Autre différence : la force électrique peut être répulsive.
La variable d'écart r étant au dénominateur et au carré, il en résulte que ces forces diminuent exponentiellement lorsque la distance augmente.
Champ
électromagnétique
De la notion de force on passe à celle de champ gravitationnel, modélisant l'influence exercée par un corps autour de lui.
Dans la section consacrée à la forme vectoriel de la force électrique (205) nous avions évoqué, via la notion de vecteur radial, le fait que si l'on déplace l'un des deux corps autour de l'autre le vecteur partant du corps immobile décrit le cercle correspondant.

La propagation de cette influence d'un corps vers l'autre ne se fait pas instantanément. Il résulte de la nature spatio-temporelle de la dynamique des forces que la propagation génère une onde (électrique, gravitationnelle). Cette onde transmet un mouvement : dans l'animation suivante celui de la main est transmis à celui de la boule rouge.

Ce sont des principes similaires qui sont appliqués dans la communication par antennes radios dipolaires (... sauf que dans le cas des ondes électromagnétiques, il ne semble pas y avoir de médiation physique (notion d'interaction "à distance").
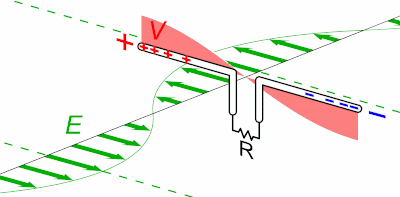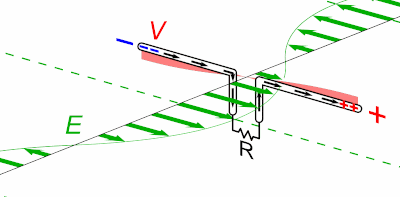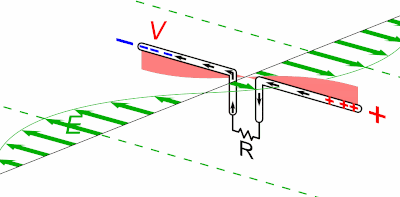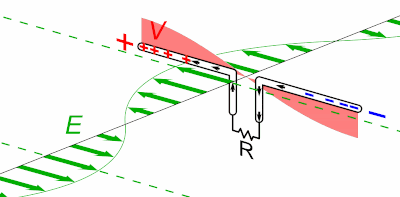
Une antenne est un fil de cuivre le long duquel les électrons se déplacent en aller-retours sous l'action de sources de tensions variables, et ce faisant provoquent une onde électrique.
L'animation suivante montre que lorsqu'un corps se déplace, le champ électromagnétique qui lui est associé n'est pas déplacé en bloc mais de proche en proche.
Dans la section #Gauss-electricite nous avions évoqué le système d'équations de Maxwell (exprimées ci-dessous dans une forme différente).
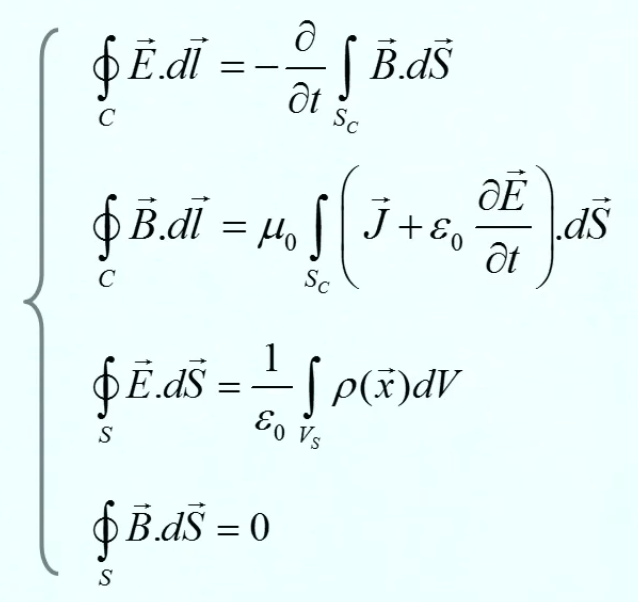
Il résulte de ce système l'équation d'onde électromagnétique ΔE→ - 1 / c 2 * ∂ 2E→ / ∂t 2 = 0 où
• ΔE→ est l'opérateur laplacien (278) du champ E→ ;
• c est la vitesse de la lumière, indiquant que les ondes électromagnétiques se propagent à la vitesse de la lumière.
Champ
gravitationnel
En réalisant un travail comparable à ceux de Maxwell sur les ondes électromagnétique, mais appliqué cette fois aux ondes gravitationnelles, Einstein a formulé théoriquement en 1916 l'existence d'ondes gravitationnelles sous la forme d'un système d'équations plus nombreuses et complexes, dont : Gμν ≡ Rμν - 1/2 * R * gμν = 8 * π * G / c 4 * Tμν
où
• Gμν est le tenseur métrique du champ gravitationnel, exprimant le fait que la gravitation est une courbure de l'espace-temps ;
• T contient la masse du corps générant le champ gravitationnel.

Le plan du graphique ci-contre représente une version simplifiée en deux dimensions de notre espace à trois dimensions, l'axe vertical représentant alors le temps (quatrième dimension). La modification de l'espace-temps par la masse de la sphère prend la forme de la courbure de l'espace représenté ici en deux dimensions ...
On notera que l'équation d'onde graviationnelle dérivée par Einstein à partir de son système d'équation est similaire à l'équation d'onde électromagnétique de Maxwell : Δh−αβ - 1 / c 2 * ∂ 2 h−αβ / ∂t 2 = 0
où
• Δh−αβ est le laplacien du tenseur qui est la solution de l'équation ;
• c est la vitesse de la lumière, indiquant que les ondes gravitationnelles se propagent aussi à la vitesse de la lumière.
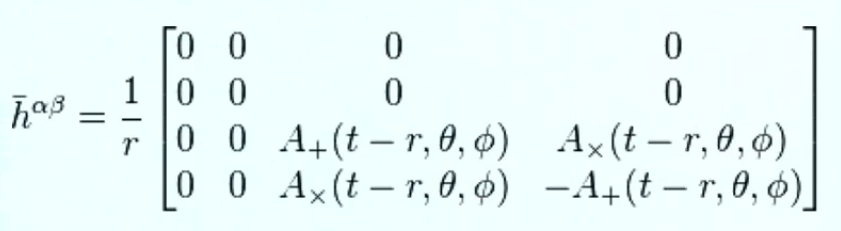
Mais il est beaucoup plus difficile de vérifier expérimentalement l'existence des ondes gravitationnelles que celles des ondes électromagnétiques, en raison de l'ordre de grandeur nettement inférieur de la force gravitationnelle. Il faut donc être en mesure d'effectuer la mesure sur des masses d'ordres de grandeur tels que les étoiles à neutron illustrée dans l'animation au début de cette section, ou encore des trous noirs.
La vidéo suivante montre que la notion de courbure de l'espace-temps à proximité d'un corps de masse non nulle permet d'expliquer le mouvement orbital.
Magnétisme
2. Pôles magnétiques
3. Champ magnétique
4. Loi de Coulomb
5. Expérience d'Oersted
6. Formule de Biot et Savart
7. Orientation du champ magnétique
8. Courant électrique et champ magnétique
9. Formule d'Ampère
10. Constante de force magnétique : définition de l’Ampère
11. Qu'est ce qu'un aimant selon Ampère ?
12. Le bonhomme d’Ampère : un mystère résolu
13. Courants de surface et physique quantique
14. Pourquoi a-t-on abandonné Ampère ?
15. Pourquoi le concept de champ ?
16. Pourquoi un champ de force pour le monopôle magnétique ?
17. Force magnétique de Laplace
18. De la force de Laplace à la force de Lorentz
De l'antiquité au moyen-âge
Soit deux aimants, l'un rectangulaire et l'autre en forme de cercle, la force d'interaction entre les deux passe de l'attraction à la répulsion selon le positionnement relatif de l'aimant en forme de cercle. Les propriétés de cette force sont donc assez complexes.
N.B. Une force d'interaction peut donc être attractive ou répulsive.

Les applications de la force magnétique sont nombreuses :
- l'électro-aimant est une masse de fer autour de laquelle passe un courant électrique ; il suffit alors de couper le courant pour que la force magnétique exercée par la masse de fer disparaisse ;
- l'aiguille de la boussole subit la force magnétique exercée dans le champ magnétique terrestre ;
- le rotor du moteur "électrique" tourne sous l'effet d'une force magnétique (PS : parler de moteur magnétique serait donc plus judicieux) ;
- lorsque le vent fait tourner une hélice éolienne, celle-ci fait tourner des aimants autour de fils électriques, y générant ainsi un courant électrique ; ...
Dès le sixième siècle av. J.-C. des savants ont décrit les propriétés apparentes du magnétisme, en observant l'attraction exercée sur le fer par une roche appelée magnétite, qui est un oxyde de fer (Fe3O4) sous forme de cristal.
Cette force d'attraction (de portée assez faible : les deux objets doivent être assez proches l'un de l'autre) est également observée si l'on frotte un morceau d'ambre (une résine fossile). Cependant les savants de l'antiquité avaient déjà remarqué que, dans le cas de l'ambre, l'interaction, que l'on qualifie aujourd'hui d'électrique, diffère de l'interaction magnétique :
- l'ambre n'exerce pas naturellement une force d'attraction : il faut pour cela la frotter ;
- l'interaction électrique est plus faible que l'interaction magnétique (l'ambre frottée peu attirer une plume mais pas un clou) ;
- la durée de l'interaction électrique n'est pas permanente, contrairement à l'interaction magnétique ;
- l'interaction électrique n'est pas transmissible, contrairement à l'interaction magnétique, qui est transmissible par contact (notion d'aimantation) ;
la durée de l'aimantation après le contact perdure (mais pas infiniment).
- l'interaction électrique s'observe sur tous types de matériaux (papier, plume, morceau de liège, ...), tandis que l'interaction magnétique ne s'observe que sur les métaux contenant du fer.
N.B. Ces propriétés reflètent l'état des connaissance à l'époque de l'Antiquité. Nous verrons cependant qu'elles doivent être nuancées.
Vers l'an cent av. J.-C., des savant chinois on conçu la boussole en constatant qu'une aiguille de magnétite flottant à la surface d'une coupelle remplie de liquide, s'orientait systématiquement dans la même direction selon un axe nord-sud. L'aiguille s'oriente ainsi toujours du côté où le soleil se situe à midi. Le chinois ont ainsi découvert, sans le comprendre, l'effet du magnétisme terrestre.
Les chinois ont découvert que pour magnétiser une aiguille de fer, il suffit de la chauffer à rouge, puis de la refroidir en la plaçant dans la direction nord-sud dans un liquide : ainsi l'aiguille a pris du magnétisme de la Terre.
Pôles magnétiques
Aux XIIIème siècle, l'ingénieur militaire français Paul de Maricourt rédiga le premier traité sur les propriétés des aimants. Ce traité fut le résultat d'expérimentations consistant notamment à fabriquer des sphères magnétiques et à observer leurs interactions. Il s'agissait de boules de bois (qui pouvaient donc flotter) sur lesquelles Maricourt fixa des morceaux de magnétite. Ceux-ci étaient orientés de telle sorte qu'une boussole appliquée sur chaque morceau de magnétite s'oriente le long d'un méridien de la sphère (pour ce faire, l'ingénieur marquait sur chaque morceau de magnétite l'orientation de l'aiguille). À l'instar du modèle planétaire, les méridiens se rejoignent en deux points, que Maricourt qualifia de "pôles".

En plaçant une telle sphère magnétique sur la surface d'une bassine remplie de liquide, Maricourt constata que la sphère s'orientait toujours dans l'axe des pôles géographiques nord et sud, et toujours par le même pôle de la sphère. Il identifia donc l'un et l'autre en les appelant tout simplement du même nom que le pôle géographique vers lequel ils s'orientent. Ce fut l'invention de la notion des pôles magnétiques.

Et lorsqu'il plaça deux sphères magnétiques dans la même bassine de liquide, Maricourt constata entre elles des forces d'interaction de deux types : attraction des pôles différents, et répulsion des pôles identiques. Ce sont là les fondements des théories actuelles du magnétisme.
Partant alors de la constatation que tout aimant est constitué de deux pôles qui ont des propriétés physiques différentes – puisque l'un est attiré par le pôle géographique nord, et l'autre vers le pôle géographique sud – Maricourt en déduisit l'existence de "substances différentes" au sein de chaque aimant, et anticipa que s'il arrivait à isoler ces deux substances, celles-ci devraient logiquement s'attirer.
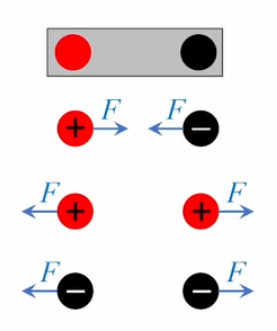
On retrouve ici des notions très semblables à celles de l'algèbre de l'électricité, fondées sur des électricités de natures différentes, qui ne seront théorisées qu'au 18° siècle (soit cinq cents ans plus tard ..., grâce aux travaux de Charles Dufay et Benjamin Franklin) avec les notions de charges positives vs négatives (cf. /matiere#cohesion-electromagnetique).
Pour vérifier sa thèse de l'existence de monopôles, Maricourt partage un aimant en deux parts. Il constate alors que celles-ci subissent certes une force d'attraction ... mais qui se transforme en répulsion dès que l'on retourne l'une des deux parts. Et reproduire l'opération de séparation sur une des parts de façon récurrente n'y changeait rien.
Maricourt n'avait donc pas réussi à isoler des monopôles. Chaque séparation d'un aimant en deux parts provoque l'apparition d'un pôle opposé/différent sur la surface de coupage. L'ingénieur constate ainsi qu'un aimant apparaît toujours sous forme de dipôle.
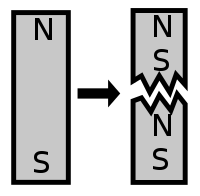
Ne renonçant pas à sa thèse malgré l'échec expérimental, Maricourt persiste, cette fois en proposant un modèle théorique, selon lequel chaque aimant serait composé de dipôles magnétiques, lesquels sont tous orientés de la même façon. Ainsi si le monopôle "nord" est toujours à gauche et le monopôle "sud" toujours à droite, alors, si l'on suppose que la surface de fracturation d'un aimant ne peut passer qu'entre deux dipôles, et non au milieu d'un dipôle, il en résulte que la face gauche sera toujours tapissées de monopôles "nord", tandis que la face sera droite sera toujours tapissées de monopôles "sud".
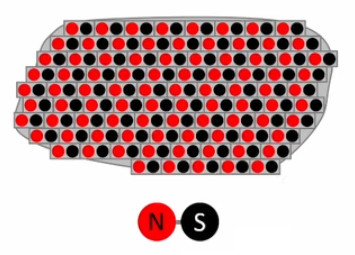
Un aimant serait composé de dipôles magnétiques, chacun composé d'un monopôle "nord" et d'un monopôle "sud". L'échec des tentatives d'isolement des monopôles s'expliquerait par la difficulté à fracturer un aimant autrement qu'en passant par les lignes des rectangles modélisant les dipôles.
Ce modèle théorique permet ainsi d'expliquer l'échec expérimental, sans pour autant abandonner la thèse de l'existence de monopôles magnétiques.
La thèse de l'existence de monopôles magnétiques fut développée mathématiquement par Paul Dirac, un des "pères" de la mécanique quantique, et prix Nobel de physique en 1933. Les monopôles magnétiques sont l'équivalent des charges électriques, mais générant un champ magnétique, et non pas électrique.

L'ensemble collisionneur-détecteur du CERN vise notamment à isoler un monopôle.
Aujourd'hui encore on n'a toujours pas réussi à isoler expérimentalement cette particule hypothétique qu'est le monopôle, malgré les moyens technologiques disponibles (cf. la taille relative de l'homme au milieu de la photo ci-contre) ...
Champ magnétique
Dans la vidéo précédente, a été introduite la notion de pôles magnétiques. Cette troisième vidéo d'introduction au magnétisme concerne la notion de champ magnétique. Celle-ci a été introduite au 16° siècle par le britannique William Gilbert, à partir du des travaux de Maricourt sur l'interaction magnétique, que l'on peut résumer comme suit :
- application technologique : le compas ;
- formalisme théorique :
- notion physique de pôles nord et sud ;
- règle de répulsion de pôles identiques vs attraction de pôles différents.
Ainsi pour Pierre de Maricourt une pierre d'aimant peut être vue comme composée de briques élémentaires (c-à-d insécables) appelées "dipôles", composées d'un pôle "nord" et d'un pôle "sud".
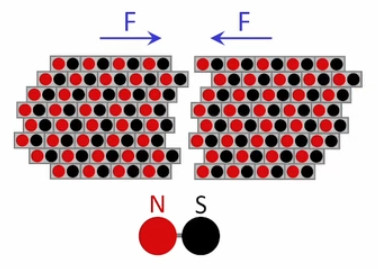
On peut ainsi expliquer théoriquement les propriétés de cet aimant, en postulant que les dipôles sont orientés dans le même sens (pôles nord d'un côté, pôles sud de l'autre). Ainsi la ligne de fracture d'un aimant brisé ne peut passer qu'entre des dipôles. Et l'on peut alors expliquer pourquoi les deux parties d'un aimant brisé s'attirent (cas du schéma ci-contre), mais se repoussent si l'on retourne l'une d'elle.

S'inspirant des travaux de Maricourt, Gilbert conçut notamment une expérience consistant à faire pendre deux clous, l'un à côté de l'autre, chacun au bout d'une ficelle. Lorsqu'on approche alors un aimant de ces deux clous, ceux-ci s'écartent. En effet, puisque le magnétisme est transmissible au fer, les deux clous sont donc magnétisés, de sorte que leurs pôles de même type se repoussent (cf. schéma ci-contre), comme prévu par le formalisme de Maricourt
Gilbert reproduit également l'expérience de Maricourt avec les sphères. Il développa l'analogie avec la Terre : la boussole se comporte de la même façon à la surface de la Terre qu'à celle de sa "Terrella" ("petite Terre"). Il en déduit logiquement que la Terre est un aimant ! Gilbert a ainsi découvert le magnétisme Terrestre.
Gilbert va cependant comprendre que Maricourt ne fut pas bien inspiré lorsqu'il choisi de nommer pôle "nord" la partie de l'aiguille aimantée s'orientant vers le pôle géographique nord de la Terre. En effet, en vertu des règles formelles de Maricourt concernant les forces d'attraction et répulsion, le pole "nord" de l'aiguille de la boussole ne peut être attiré que par le pôle magnétique ... sud de la Terre ! Par conséquent, le pôle géographique nord de la Terre correspond à son pôle magnétique sud (et inversement : au sud géographique de la Terre, se trouve son pôle magnétique nord).
Si Maricourt n'est pas allé aussi loin que Gilbert, c'est parce qu'il ne croyait pas à l'effet de la Terre sur les phénomènes qu'il observait lors de ses expériences : il n'a pas considéré la thèse que la Terre soit elle-même un aimant. Pour lui, l'aiguille de la boussole était attirée par un corps extra-terrestre, en l'occurrence l'étoile polaire (ce qui implique que l'axe de la Terre soit orienté vers celle-ci...). Et c'est précisément en raison de ce postulat non pertinent qu'il a fait le choix non pertinent d'appeler nord" le pôle de son aimant orienté vers le pôle géographique nord de la Terre. Sans cette erreur de jugement de la part de Maricourt, nous n'aurions pas eu cette inversion de nomenclature entre pôles magnétique et géographique de la Terre.
N.d.A. On peut se demander pourquoi les scientifiques n'ont pas corrigé cette nomenclature. J'image que c'est afin de préserver la cohérence avec les écrits anciens.
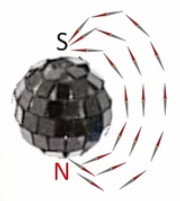
Gilbert va pousser plus loin son apport scientifique, par des expériences consistant à observer l'effet de la variation de la distance entre boussole et Terrella. Il va en déduire l'existence de lignes de force magnétique, le long desquelles l'aiguille aimantée est orientée.
L'existence de ces lignes de force fut exposée de façon très visuelle quelques années plus tard, par une expérience réalisée par Descartes, consistant à placer un aimant en dessous d'une feuille de papier sur laquelle repose de la limaille de fer. Les brins de limaille s'orientent alors comme dans l'illustration ci-contre.

Ces lignes de force sont orientées : le pôle nord de l'aiguille étant attirée vers le pôle magnétique sud de la Terre. À chaque ligne de force est donc associée une direction (rappel : une force est toujours caractérisée par une direction dans l'espace). Celle-ci est représentée par une flèche, en tous points autour de la sphère.
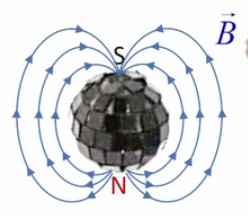
La sphère est ainsi décrite comme générant un champ magnétique. Celui-ci est noté B→. Il s'agit d'une grandeur physique assez abstraite, mais permettant de caractériser ce qui se produit dans l'environnement de la sphère aimantée, en termes de forces (N.d.A. : "cartographie" de l'orientation de l'aiguille de la boussole).
On utilise indifféremment les expressions "ligne de force magnétique" ou "ligne de champ magnétique".
On sait depuis le 19° siècle que le champ magnétique terrestre est indispensable à la vie sur Terre, car il protège celle-ci de rayonnements cosmiques ionisants (composés de particules chargées) émis par le soleil. En effet, le champ magnétique terrestre agit comme un bouclier qui détourne ce rayonnement solaire.

Willam Gilbert a également étudié l'effet de la chaleur sur le magnétisme. Il a montré qu'en chauffant suffisamment un aimant, on lui fait perdre son magnétisme : son champ magnétique disparaît. Ce phénomène s'explique toujours par le formalisme des dipôles de Maricourt : au-delà d'une certaine température, l'agitation thermique a pour effet de briser l'organisation spatiale des dipôles.

Sous l'effet de la chaleur, les dipôles ne sont plus orientés dans le même sens.
Loi de de Coulomb
Cette quatrième et dernière introduction au magnétisme est consacrée à la loi de Coulomb pour le champ magnétique. Rappelons que Coulomb est le premier à avoir (au 18° siècle) énoncé la loi de force électrique en 1 sur r carré F→ = kC * q2 * q1 / r 2 * 1r→ (205).
C'est donc deux siècles après William Gilbert que Coulomb va identifier une forte analogie entre lignes de force magnétique et lignes de force électrique. Cette analogie conduit à la notion de champ d'un dipôle magnétique (la charge positive étant associée au pôle nord, et la charge négative au pôle sud) : l'aimant génère donc dans l'espace un champ dipolaire.
Sauf qu'on ne parle toujours pas de "champ", mais seulement de "lignes de forces". Celles-ci sont des lignes abstraites de l'espace, indiquant la direction dans laquelle s'oriente une aiguille de boussole.
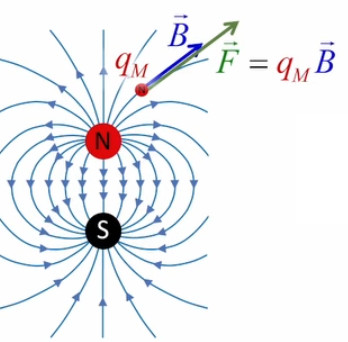
Le principe du champ magnétique est le même que pour le champ électrique : si l'on pouvait placer dans ce champ un monopôle magnétique (nord ou sud) dont on connaissait la "charge magnétique", la notion de champ permettrait alors de mesurer la force magnétique exercée sur cette charge par le champ. Ainsi, par rapport à F→ = q0 * E→ (206), on a donc simplement remplacé q0 par qM, et E→ par B→ :
F→ = qM * B→
Mais revenons à Descartes. À cet époque (17° siècle), on pensait que si l'on pouvait isoler un monopôle magnétique, celui-ci générerait des lignes de force dans l'espace, qui se distribueraient dans toutes les directions de façon isotrope, donc à l'image de ce qui se produit avec une charge électrique et le champ qu'elle génère dans son environnement. Nous avons vu que ce champ est radial (cf. (204) ), et que son module diminue en 1 sur r2, où r est la distance à partir de la charge q : E→ = kC * q / r 2 * 1r→ (207).
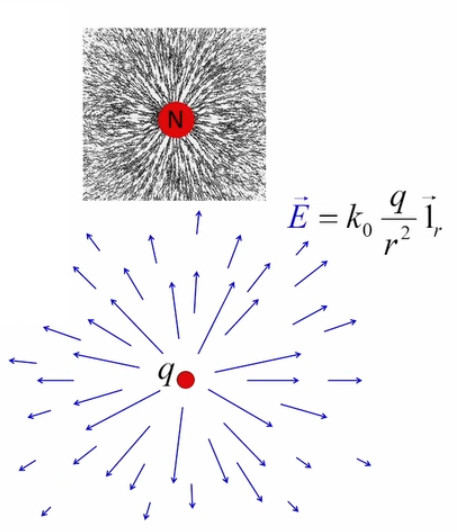
À l'époque de Coulomb, le "consensus scientifique" était que ce que nous appelons aujourd'hui le champ magnétique obéissait à la même loi. Pour le vérifier, Coulomb a utilisé le même instrument que pour mesure la force électrique : une balance à torsion.
La balance de Coulomb est composée de deux tiges aimantées, dont l'une est celle d'une sorte de boussole. L'intérêt d'utiliser deux aimants allongés est qu'ainsi les deux pôles instrumentalisés pour mesurer la force exercée par la tige verticale sur celle de la boussole ne sont influencés que de façon négligeable par le pôle opposé de la tige verticale.
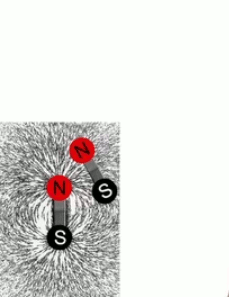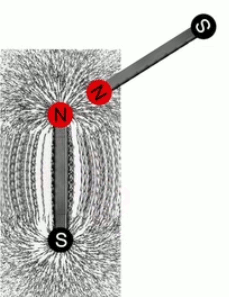
Les deux pôles nord se situent sur le plan de la règle circulaire de la boussole, de sorte qu'en faisant varier la distance r entre ceux-ci, la balance à torsion peut alors mesurer la force correspond à un déplacement de l'aiguille de boussole le long de sa règle circulaire. Coulomb a ainsi pu mesurer que cette force varie en 1 sur r2 : F→ ∝ 1 / r 2 * 1r→
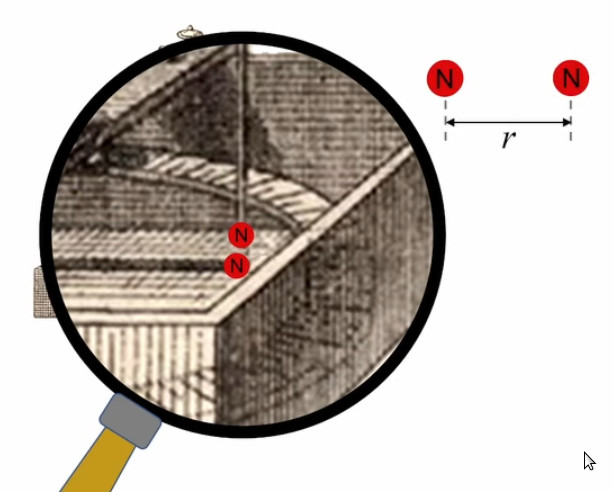
Cette constatation expérimentale conduit Coulomb à une extension de la théorie, fondée sur une analogie entre forces magnétique et électrique : dans E→ = kC * q / r 2 * 1r→ (207), il remplace simplement q par qM, kC par kM, et bien sûr E→ par B→ ⇒
B→ = kM * qM / r 2 * 1r→
soit le champs magnétique d'un monopôle magnétique de charge qM.
Dans la prochaine vidéo, nous verrons que l'analogie entre forces magnétique et électrique a été remise en question par le suédois Hans Ørsted (19° siècle), qui a exposé non pas une analogie mais une interaction entre électricité et magnétisme. Mais avant de poursuivre, voyons un autre exemple illustrant les limites de l'analogie ...
Magnétisme
animal
Terminons cette dernière séance d'introduction en évoquant un contemporain de Coulomb, le médecin allemand Franz Mesmer. Celui-ci affirmait soigner ses patients à l'aide du champ magnétique d'un aimant. Mais ses affirmations n'étaient que des croyances car, contrairement à Coulomb, elles ne reposaient pas sur une méthode scientifique de mesures et vérifications des mesures.

Cependant la méthode de Mesmer connaissait un succès non négligeable auprès des patients, ce qui l'encouragea à développer sa méthode thérapeutique en s'inspirant de la théorie du magnétisme. Ainsi son raisonnement était que puisque le corps humain est sensible au champ magnétique, c'est donc que lui-même possède des propriétés magnétiques (le corps humain serait donc fait de dipôles magnétiques). Il en conclut qu'un aimant n'était pas nécessaire pour soigner, et que ses mains suffisaient, c-à-d qu'il pouvait utiliser son propre magnétisme.
Cependant le consensus scientifique fut rapidement que le corps humain n'est pas composé de dipôles magnétiques : ainsi le corps humain n'a pas d'effet sur une boussole. La réponse de Mesmer consista à inventer la notion de "magnétisme animal" (aussi appelé "mesmérisme"), par opposition au "magnétisme minéral", et dont la nature serait différente (ce qui expliquerait l'absence d'effet sur une boussole).
Une explication plus rationnelle des succès thérapeutiques de Mesmer (nombre des patients de Mesmer se sont déclarés guéris par sa méthode "magnétique") est que les séances de magnétisme qu'il appliquait à ses patients étaient – en raison de son intime conviction, et du pouvoir de conviction qu'elle peut induire – des "de facto" séances d'hypnose. Or on sait aujourd'hui que l'hypnose peut avoir des effets thérapeutiques. Mesmer aurait ainsi découvert un véritable procédé thérapeutique (hypnose), mais en croyant exploiter un phénomène d'une autre nature (magnétisme animal).
En anglais, une personne hypnotisée est parfois dite "mesmerized".
Ceci dit, on sait aujourd'hui qu'il existe une forme de magnétisme "animal", mais qui est en fait fondé sur le magnétisme minéral. Ainsi la photo ci-contre montre une bactérie, appelée Magnetospirillum, contenant une chaîne de cristaux de magnétite, permettant à la bactérie de s'orienter parallèlement aux lignes du champ magnétique terrestre.
D'autres animaux sont équipés d'organes magnétorécepteurs (c-à-d sensibles aux champs magnétiques) leur permettant de s'orienter, tels les oiseaux migrateurs, dont la rétine contient une molécule composée d'une grande protéine (cf. /biologie#proteines) appelée cryptochrome, qui est sensible aux champs magnétique en présence de lumière.
Expérience d'Oersted
Au début du 19° siècle le suédois Hans Œrsted a réalisé une expérience révélant une interaction entre électricité et magnétisme, deux phénomènes alors considérés comme séparés. Cette expérience consistait à constater que l'échauffement (mesuré par Δ T) d'un câble reliant les deux bornes d'une pile de volta (inventée quelques années plus tôt) s'accompagnait d'un effet sur une boussole placée à proximité : son aiguille est déviée.
À priori, cette interaction pouvait être vue pour assez banale, car on avait déjà observé que les éclairs naturels avaient le même effet sur les boussoles (ce qui avait d'ailleurs été la cause de naufrages). Mais on avaient alors expliqué cette interaction par un rôle intermédiaire attribué à la chaleur très importante générée par la foudre qui tombe (plusieurs dizaines de milliers de degrés). Par ailleurs, William Gilbert avait déjà constaté que la chaleur peut modifier le champs magnétique d'un aimant (suffisamment élevée, elle peut même provoquer sa disparition) :
ΔE→ ⇒ Δ T ⇒ ΔB→
Or dans l'expérience d'Œrsted, la température dégagée est trop faible que pour pouvoir être considérée comme étant la cause de l'effet coïncidant sur le magnétique terrestre. L'expérienc d'Œrsted révélait donc un lien direct, c-à-d une interaction entre électricité et magnétisme :
ΔE→ ⇒ ΔB→
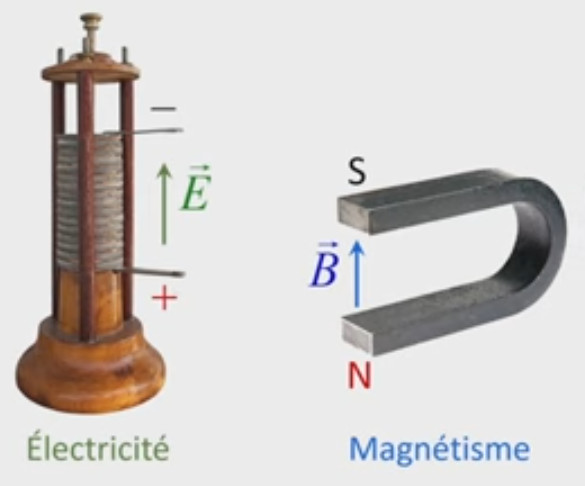
Mais il restait à expliquer pourquoi la boussole – supposée ne réagir qu'au champ magnétique, lui même du aux charges magnétiques selon B→ = kM * qM / r 2 * 1r→ (283), et n'affectant que des charges magnétiques (pôle nord de l'aiguille de boussole, attirée par le champ généré par le pole nord d'un aimant) – est déviée, alors que la pile de volta n'est pas un objet magnétique. La pile ne génère qu'un champs électrique, lequel ne concerne que les charges électriques, selon E→ = kC * q / r 2 * 1r→ (207).
Or quand le circuit de la pile est est fermé, cela provoque une réaction de l'aiguille de la boussole. On devine alors que cette réaction pourrait être provoquée par le courant électrique (de la borne + vers la borne -), généré par la fermeture du circuit selon la loi d'Ohm V = R * I (261). C'est donc que ce courant électrique génère un champ magnétique ! Mais la loi d'Ohm ne sera formulée que sept ans après l'expérience d'Œrsted ...
Formule de Biot et Savart
Biot et Savart ont poussé plus loin l'expérience d'Œrsted, en mesurant le phénomène, et en établissant une équation permettant de le formuler mathématiquement.
Pour reproduire l'expérience d'Œrsted, Biot et Savart ont placé, à côté de la pile de volta, une longue tige métallique, au travers de laquelle ils faisaient passer un courant électrique en la reliant à la pile de volta au moyen de câbles électriques. Enfin une aiguille de boussole, placée au sommet d'une fine tige, allait leur permettre de mesurer les forces magnétique générée dans l'environnement du courant électrique. En effet, dans un tel montage, l'aiguille se place dans une position imposée par ces forces magnétiques (cf. infra, les détails du système expérimental).
Deux forces magnétiques opposées apparaissent, sur les pôles nord et sud de l'aiguille. La direction de celle-ci indique la direction du champ magnétique puisque le pôle nord est associé à une charge magnétique qM positive, et le pôle sud à une charge négative : F→ = qM * B→ (282).
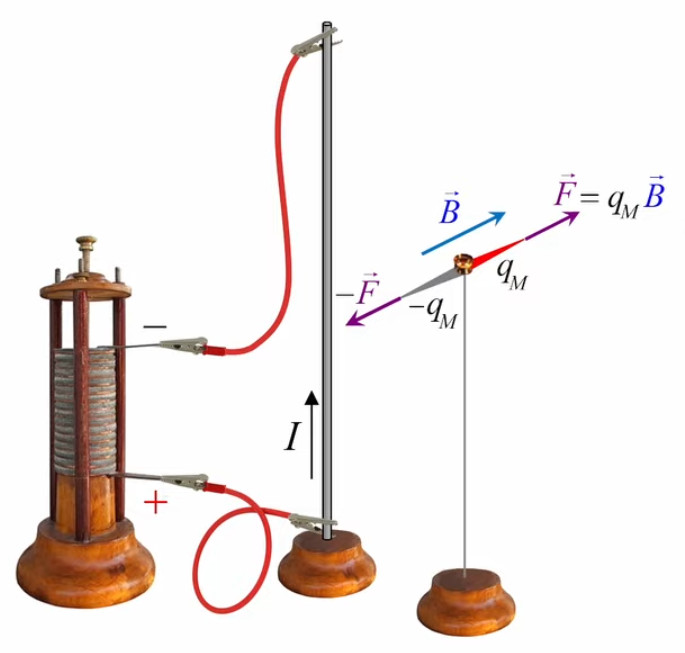
Pour garantir que l'aiguille se place dans une position imposée par ces forces magnétiques, le système expérimental devait être affranchi :
des forces de frottement ⇒ afin de les rendre négligeables, la tige mince se termine en une pointe sur laquelle repose une encoche conique située au centre de l'aiguille magnétique ;
de la gravitation ⇒ le point d'application de la tige verticale dans l'encoche de l'aiguille magnétique est située au centre de gravité de celle-ci, de sorte que la gravitation n'a pas d'effet sur sa position ;
du champ magnétique terrestre (qui oriente l'aiguille vers le pôle nord géographique de la Terre) ⇒ Biot et Savart ont placé une série d'aimants dans l'environnement du système expérimental, de manière à compenser le champs magnétique terrestre ⇒ en l'absence de courant, ce champ magnétique inverse a pour effet que l'on obtient finalement un champ virtuellement nul.
Dans ces conditions, l'aiguille magnétique peut alors être placée dans toutes les positions, et y demeurer, tant qu'elle ne subit pas de force due au courant.
Lorsque celui-ci est activé, on constate alors que l'aiguille se place :
- horizontalement c-à-d, plus précisément, perpendiculairement à sa tige. Celle-ci étant parallèle à la tige du courant, on en déduit que les forces exercée par ce courant sont aussi perpendiculaires à celui-ci ;
- dans un plan perpendiculaire au rayon reliant les deux tiges, de sorte que l'aiguille est dite parallèle (fait face) au courant.
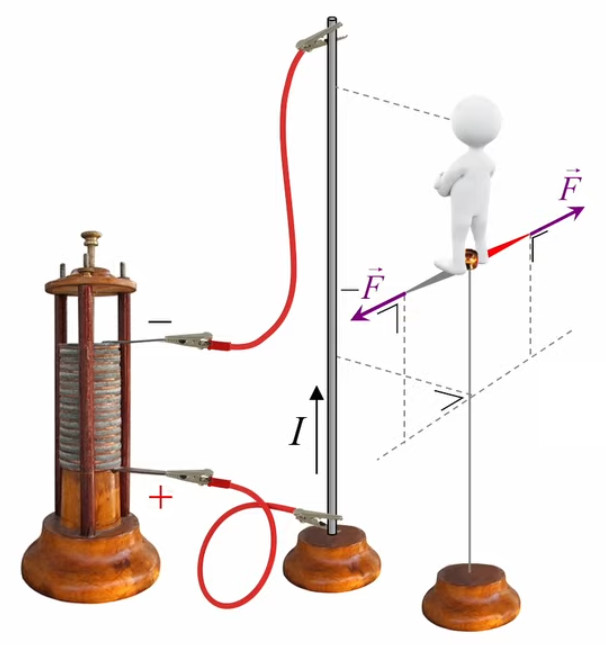
Ces faits sont observés, quelle que soit la position de la tige fine dans l'environnement de la tige du courant.
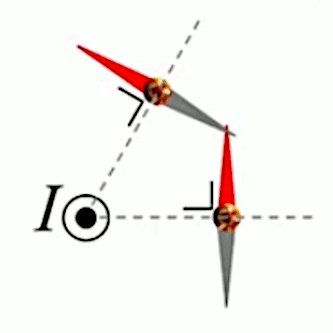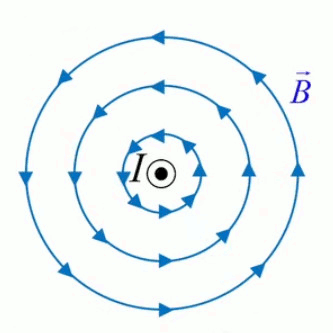
Si l'on observe par le haut ces variations de position de la tige fine, on constate que les lignes du champ magnétique généré sont circulaires, puisque l'aiguille est systématiquement perpendiculaire au rayon entre les deux tiges.
Le symbole "pointe de flèche" au centre du schéma ci-contre montre que le courant est dirigé vers un point d'observation situé à la verticale du système.
Ces lignes de champ magnétique circulaires sont toujours orientées dans le sens "pôle nord vers pôle sud" des aiguilles.

Pourtant, la loi de Coulomb des champs magnétiques B→ = kM * qM / r 2 * 1r→ (283), correspond plutôt à des lignes de champ radiales, émergeant du pôle nord, et se rejoignant au pôle sud des sphères expérimentales de Maricourt et de Gilbert. Or avec l'expérience de Biot et Savart, il n'y a plus de pôles !
L'équation ci-dessus repose sur une supposition (dérivée du champ électrique) : l'existence de pôles magnétiques. Or on n'arrivait pas (et c'est encore le cas aujourd'hui) à isoler de pôles magnétiques ...
Moteur
magique ?
Cette différence dans la configuration du champ a une conséquence notable : un monopôle magnétique subit une force qui par définition est tangentielle à la ligne de champ, de sorte que si cette charge est reliée à l'axe du courant au moyen d'un bras de levier (cf. illustration ci-dessous), alors ce monopôle est entraîné dans un mouvement fournissant un travail qui accélère sans fin cette charge magnétique (pour autant que les forces de frottement soient non significatives) : force constante en déplacement --> travail qui accélère la vitesse --> énergie cinétique qui semble croître à l'infini.
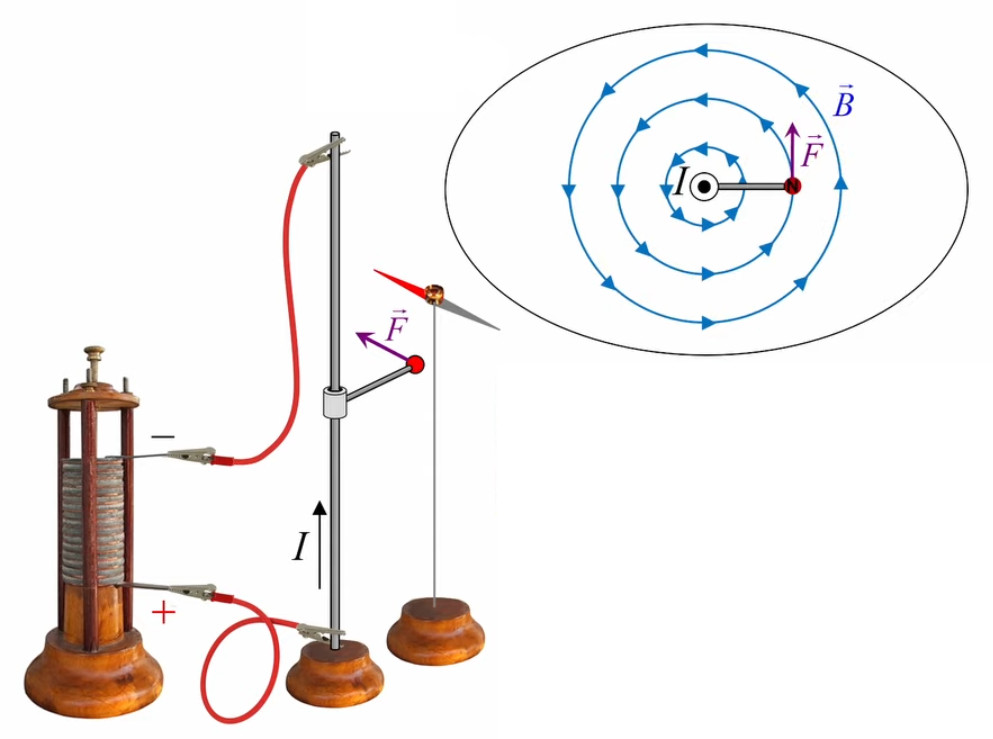
La petite boule rouge représente un supposé monopôle magnétique nord (charge magnétique positive). Celui-ci serait théoriquement entraîné dans un mouvement rotatif autour de l'axe, infiniment accéléré ... (NB : ce n'est pas le cas de l'aiguille aimantée car celle-ci constitue un dipôle, et subit donc deux forces opposées, qui s'annulent donc).
Dans un champ électrique (E→), cette situation ne se produirait pas, précisément parce que la force subie par la charge est radiale, de sorte qu'il n'y a pas de mouvement rotatif. Certes, en dissociant axe rotatif et charge générant le champ (cf. illustration 2D ci-contre), un mouvement rotatif sera enclenché par la force du champs électrique, mais très rapidement contrecarré par cette même force.
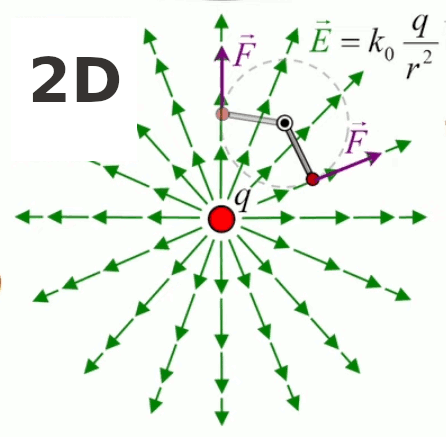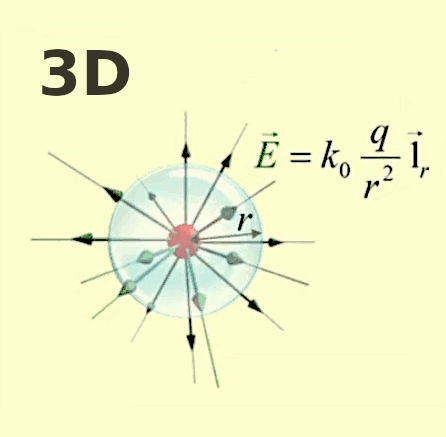
Champ électrique : symétrie radiale, encore dite sphérique.
C'est pourquoi le champ électrique est dit conservatif, tandis que le champ magnétique est dit non conservatif (on arrive donc à créer de l'énergie ex nihilo, et à l'accumuler, à priori, infiniment).
Le champ magnétique est ainsi caractérisé par une symétrie cylindrique : soit un rayon déterminé r, tous les points situés sur la surface du cylindre, correspondant à ce rayon r autour de l'axe du courant, subit la même force magnétique, quelle que soit la longueur de l'axe : l'effet de celui-ci est invariant par translation verticale, comme par rotation horizontale.
L'illustration précédente montre que la structure du champ électrique est également symétrique, mais de forme sphérique (champ radial).
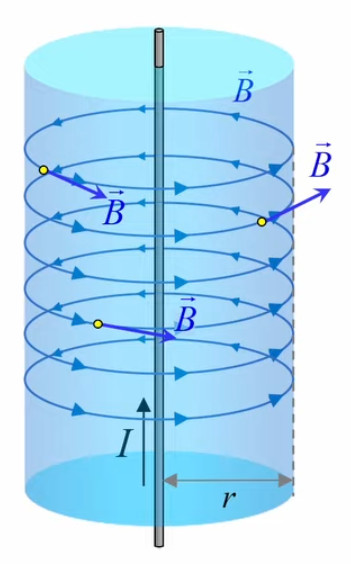
Champ magnétique : symétrie cylindrique.
Ainsi, alors que le champ électrique n'est fonction que du rayon (distance par rapport à la source du champ), le champ magnétique est fonction du rayon r et du courant I (intensité de la source du champ) : B→(I, r).
Pour modéliser ces propriétés en une équation, il faudrait procéder à des mesures sur un système composé d'une charge magnétique isolée : puisque F→ = qM * B→ (282), il suffirait alors de mesurer F→, puis de diviser cette valeur par la charge qM pour trouver la valeur du champ.
L'intérêt de connaître la valeur du champ magnétique B→ correspondant à un certain courant est que la connaissance de cette valeur permet de prédire les forces qui apparaîtront dans un système magnétique de courant I, sur une charge située à une distance r de celui-ci : .
Malheureusement, encore à ce jour, on a toujours pas réussi à isoler de monopole magnétique ... Tout ce dont disposaient Biot et Savart, c'était des dipôles magnétiques : les aiguilles magnétique composées de pôles nord et sud. Avec ces aiguilles magnétiques, ils disposaient donc bien d'un objet pour mesurer les forces en action. Mais la force totale s'exerçant sur l'aiguille est nulle ...
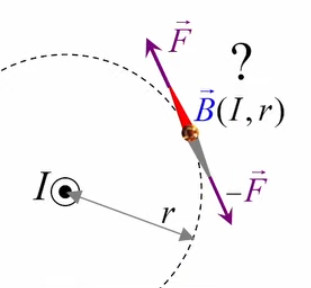
Pour contourner ce problème, Bio s'est inspiré de ce qu'il avait appris lorsqu'il était assistant de Coulomb. Ce dernier avait développé une technique de mesure indirecte, basée sur la théorie de Newton. Son principe est que lorsqu'on éloigne l'aiguille de sa position d'équilibre, elle tend à y revenir. Et comme l'aiguille peut tourner librement autour de son axe, ce retour va se faire sous forme d'une oscillation. Or la mécanique de Newton montre que cette oscillation est proportionnelle aux forces F→ et -F→ exercées respectivement sur les pôles nord et sud : F ∝ f 2 où f est la fréquence d'oscillation. Biot et Savart ont ainsi constaté qu'en divisant le rayon par un facteur n (modification de la "condition initiale" r), ils augmentaient l'oscillation d'un facteur √n, ce qui, en vertu de la règle de proportionnalité précédente, implique que la force est multipliée par (√n)2 = n. Notre équation de proportionnalité devient donc F ∝ 1 / r
Biot et Savart appliquent ensuite le même principe, en faisant varier une autre condition initiale : non plus le rayon r mais le courant I. Ils constatent ainsi qu'en multipliant le courant par un facteur n, la fréquence d'oscillation est augmentée par le même facteur √n, de sorte que la force est nécessairement multipliée par le même facteur (√n)2 = n. Notre relation de proportionnalité devient donc F ∝ I / r où la valeur du courant I apparaît au dénominateur.
Et comme F→ = qM * B→ (282), il en résulte que la même relation de proportionnalité vaut pour B ∝ I / r.
Coulomb avait montré la même relation de proportionnalité pour le champ électrique.
On obtient alors la formule de Biot et Savart en formalisant la proportionnalité au moyen d'une constante de force magnétique kM ⇒ B = kM * I / r
Biot et Savart n'ont pas mesuré la constante kM de force magnétique. Cela sera rendu possible grâce aux travaux d'Ampère, que nous verront plus loin.
La version vectorielle s'écrit en introduisant le vecteur unitaire perpendiculaire 1→⊥ :
B→ = kM * I / r * 1→⊥
Ce vecteur unitaire est perpendiculaire car la force magnétique exercée par le courant est perpendiculaire au rayon (et au courant).
Or Coulomb, qui faisait une analogie avec le champ électrique, avait plutôt proposé B→ = kM * qM / r 2 * 1r→ (283), dont la formule de Biot et Savart diffère en trois points :
- la charge électrique qM est remplacée par le courant I ;
- r 2 devient r ;
- le rayon unitaire radial devient perpendiculaire.
Alors qu'en est-il finalement ? C'est ce que nous verrons dans les vidéos suivantes, consacrées aux travaux d'Ampère sur les liens entre courant électrique et champ magnétique.
Orientation du champ magnétique
Comment déterminer formellement l'orientation du champs magnétique dans l'expérience d'Œrsted ?
Le vecteur unitaire perpendiculaire 1→⊥ de la formule de Biot et Savart B→ = kM * I / r * 1→⊥ (284) indique que l'aiguille de la boussole se place toujours dans un plan perpendiculaire à un rayon émanant du conducteur.
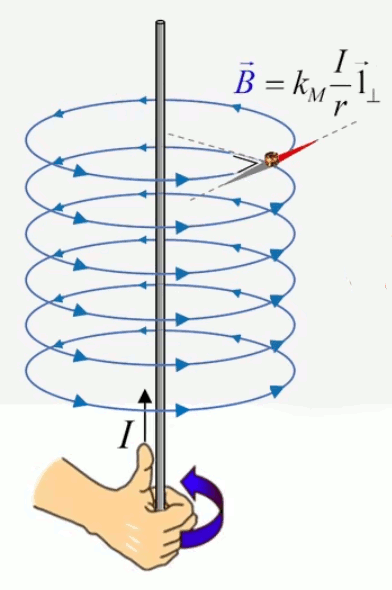
D'autre part, le pôle nord de l'aiguille est toujours orienté dans le sens illustré sur l'image ci-contre, étant donné le sens du courant dans le conducteur. Le pôle nord étant toujours tiré dans le sens du champ magnétique (et le pôle sud dans le sens opposé), il indique donc ce sens.
Cependant, le vecteur unitaire perpendiculaire ne dit rien à cet égard : si le pôle nord était orienté dans l'autre sens, on aurait toujours la perpendicularité ! Pour déterminer ce sens, il suffit d'appliquer la règle de la main droite (comme dans le cas du produit vectoriel : /geometrie#produit-vectoriel-definitionn) : en empoignant de la main droite l'axe conducteur avec le pouce dans le sens du courant, alors les doigts repliés de la main indiquent le sens du champs magnétique généré par ce courant.
Mais pourquoi la nature a-t-elle "choisi" ce sens là, plutôt que l'autre ? Ampère fournira une réponse à cette question...
Courant électrique et champ magnétique
L'expérience de Oersted avait déjà mis en évidence le lien entre courant électrique et champ magnétique (cf. supra). Cependant, la formule de Biot et Savart B→ = kM * I / r * 1→⊥ (284) – qui est la traduction mathématique de cette expérience – n'était pas entièrement maîtrisée car la notion physique de courant électrique n'avait pas encore été découverte. Ce n'est qu'un an plus tard, grâce aux travaux d'Ampère, que le terme I de cette formule sera considéré comme exprimant la notion de courant.
Cette vidéo est consacrée au cheminement intellectuel d'Ampère dans sa démarche vers la découverte du lien entre courant électrique et champ magnétique.
Violation
Newton
Commençons ce cheminement en évoquant la règle de la main droite (cf. vidéo précédente), qui conduisait à un problème conceptuel. En effet, si l'on considère un monopôle magnétique positif (nord) qM (cf. schéma ci-dessous), celui-ci subit une force dans le sens du champ magnétique, et cela tout au long de la ligne de champ circulaire, et cela infiniment, même avec des forces de frottement, de sorte que l'on pourrait ainsi accumuler de l'énergie (en l'occurrence cinétique) ... infiniment ! Or cela viole le principe de conservation de l'énergie.
Analysons ce problème au regard de la troisième loi de Newton (169) : cette loi, qui stipule que les forces apparaissent par couple de forces opposées, n'est clairement pas vérifiée dans le système d'interaction entre le conducteur et la particule, ce qui conduit au viol du principe de conservation de l'énergie.
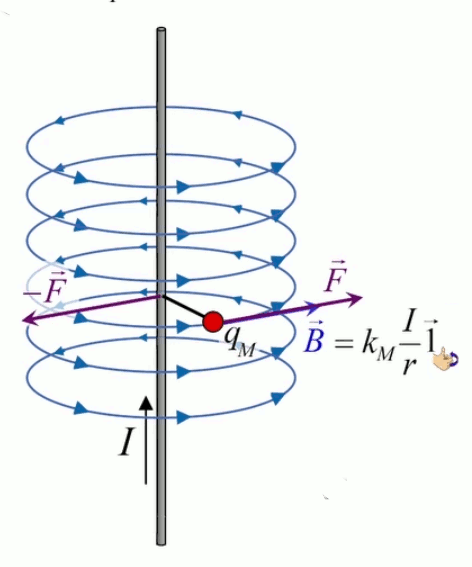
Objectif : imaginer un modèle théorique compatible avec la troisième loi de Newton.
Et la raison pour laquelle la troisième loi de Newton n'est pas vérifiée, c'est que dans ce système les forces en présence ne sont pas sur la même droite support, de sorte qu'il n'y a pas réciprocité. Ainsi, comme illustré dans l'illustration ci-dessus, si l'on faisait subir à l'axe conducteur un force de direction opposée à celle que subit le monopôle du fait du champs magnétique, celle-ci ne serait pas pour autant neutralisée car, bien qu'étant de directions opposées, les deux forces en présence ne le sont pas sur la même droite support. Par conséquent, si le fil conducteur était relié au monopôle, le système qu'il formerait se mettrait en rotation ... infinie.
Pour analyser cette situation "en creux, observons comment/pourquoi la loi de force électrique F→ = kC * q2 * q1 / r 2 * 1r→ (205) obéit à la troisième loi de Newton.
L'animation ci-dessous illustre le fait que dans l'interaction entre deux charges électrique q1 et q2, il y a réciprocité : chacune génère un champ, auquel l'autre charge est sensible. Or, comme le champ électrique est radial, les forces F→1,2 et F→2,1 que subissent respectivement les charges q1 et q2 en raison du champ généré par l'autre, sont nécessairement de mêmes modules et de directions opposées. Autrement dit, l'interaction électrique obéit à la troisième loi de Newton.
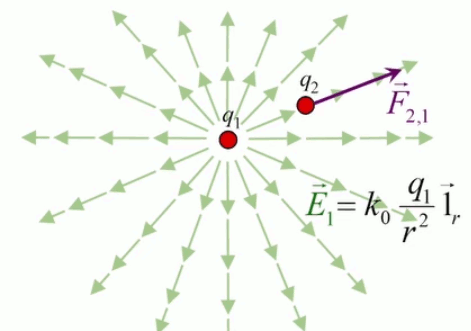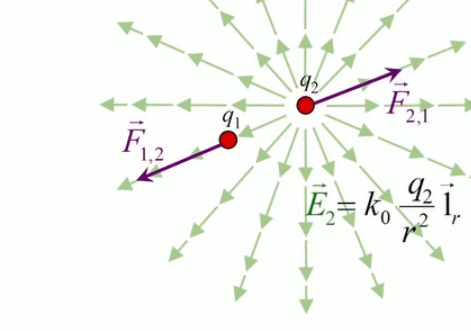
L'interaction électrique est réciproque, et respecte donc la troisième loi de Newton.
Mais l'interaction magnétique est manifestement différente de l'interaction électrique :
- la force générée par le champ magnétique n'est pas radiale mais perpendiculaire au rayon joignant l'axe et le monopôle ;
il n'y a pas réciprocité car les deux corps en interactions ne sont plus ici de même nature : alors que l'interaction électrique concerne deux charges électrique, l'interaction magnétique concerne un courant électrique et un monopôle magnétique. Or, à priori, il n'y a aucune raison pour que le courant électrique soit sensible au champ magnétique (ce sont les supposés monopôles magnétiques qui le sont, pensait-on).
Courant
Pour résoudre la violation théorique de la troisième loi de Newton, Ampère va abandonner la notion de dipôle magnétique (qui constituait le "consensus scientifique" depuis six siècles !), pour lui substituer la notion de courant ("moléculaire"), comme source des lignes de force magnétique. Selon lui, l'axe du système serait un conducteur, c-à-d qu'il laisse passer en son sein des particules provenant de la pile, et qui sont libérées par la connexion entre ses pôles. Et, imagine Ampère, c'est précisément ce courant (et non des dipôles magnétiques), qui génère un champ magnétique.
Rappelons qu'à l'époque, la notion de courant électrique (cf. la flèche verticale dans le schéma) n'existait pas encore. Le I de B→ = kM * I / r * 1→⊥ (284) désigne l'intensité du "choc moléculaire", terme utilisé par Oersted (sans pour autant connaître la nature physique de ce choc) pour énoncer le phénomène se produisant lorsque l'axe conducteur est relié à la pile de volta. Ampère va introduire la notion de courant, cependant celui-ci n'est pas encore qualifié d'électrique (car les électrons sont encore inconnus) mais de "moléculaire".
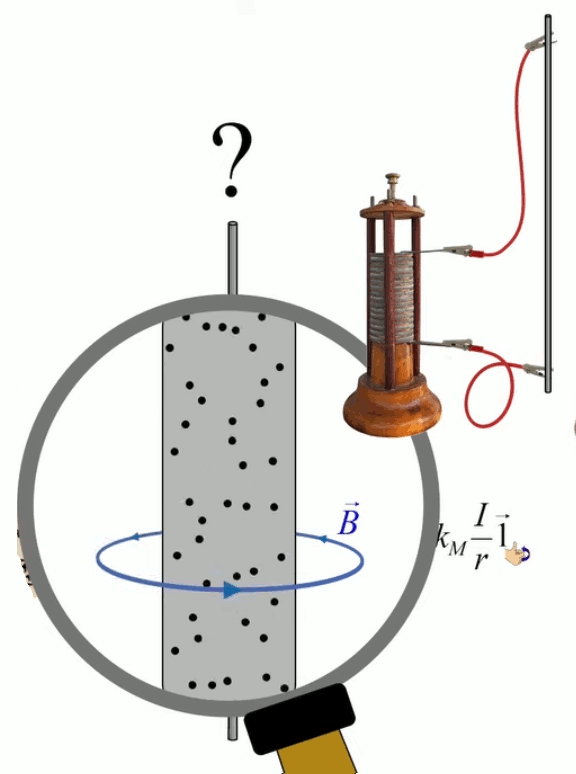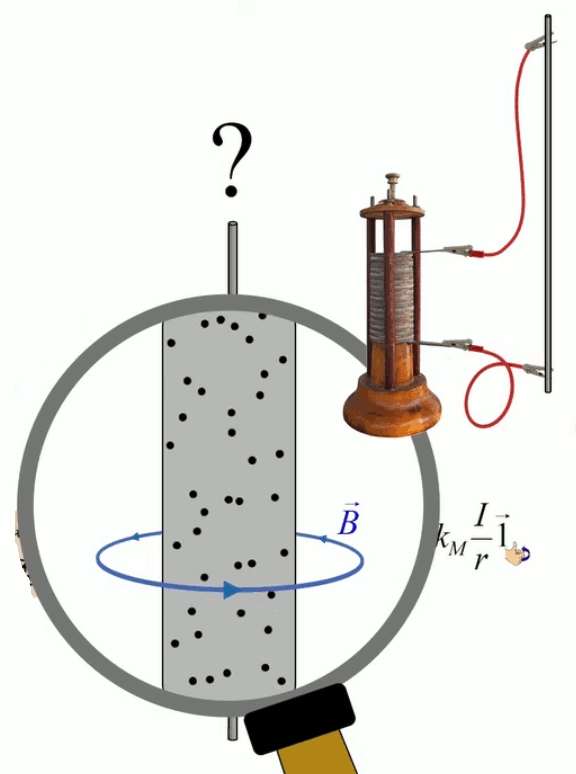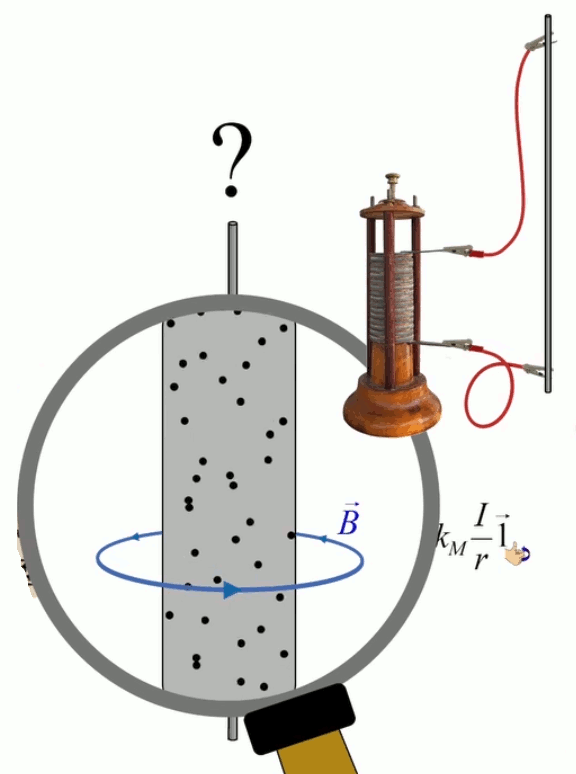
Le courant électrique génère le champ magnétique B→
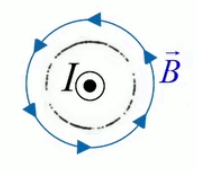
Le même système vu à la verticale
Ce changement de paradigme – par lequel la force magnétique générée par le champ magnétique s'exerce non pas sur un monopôle magnétique mais sur un courant de particules – va permettre de faire un parallèle très proche avec la théorie de l'électricité, et partant, d'en étendre le principe de réciprocité à l'interaction magnétique :
- le champs électrique est généré par une charge électrique ;
- le champ magnétique est généré par un courant électrique (et non par des dipôles magnétiques) ;
- tout comme la charge électrique est à la fois agent et objet du (c-à-d sensible au) champ électrique, le courant électrique est à la fois agent et objet du champ magnétique.
Ampère adapte donc son système expérimental, en remplaçant l'aiguille aimantée tournant autour d'une axe conducteur, par un second axe conducteur de courant. Les deux schémas suivants montrent deux points de vue du même système expérimental : de profil et à la verticale. On y voit clairement les deux forces, opposées et radiales, qui par conséquent vérifient la troisième loi de Newton.
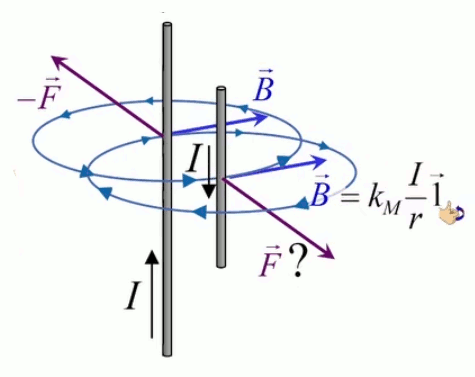
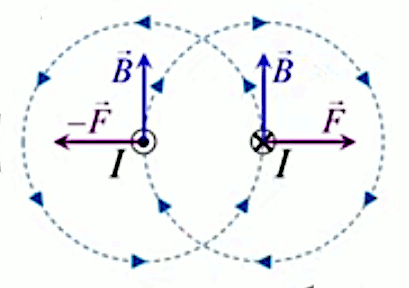
Et Ampère constate ainsi expérimentalement que son modèle respecte la troisième loi de Newton, par cette symétrie de réciprocité : il observe effectivement des forces radiales, à l'instar du champ électriques. La vidéo suivante montre le résultat de cette expérience. Le système est composé de deux fils conducteurs verticaux. L'un est relié au pôle positif (rouge) d'une source de tension, l'autre au pôle négatif (bleu). À leur base les deux fils conducteur sont fermés sur eux-mêmes, de sorte qu'un courant y peut circuler (du + vers le -). Ces fils constituent donc deux axes dans lesquels circule un courant dans des directions opposées. Et l'on constate que, effectivement, lorsque l'opérateur augmente la tension, les deux fils s'écartent légèrement.
Mais il subsiste une question : si les monopôles magnétiques n'existent pas, comment alors un aiment peut-il générer un champ magnétique ? Comment des courants (en l'occurrence, transverses) pourraient circuler en permanence dans tout aimant, sans source de courant ?
Il sera répondu à cette question dans la prochaine vidéo. Mais avant de poursuivre, reformulons les travaux d'Ampère de façon moderne, c-à-d au regard de nos connaissances actuelles.
Aujourd'hui on explique ce qu'est le courant électrique par la nature de ce qu'est un conducteur électrique, à savoir un matériaux composé d'atomes. Ceux-ci ont pour particularité de donner un électron à la matrice cristalline qu'ils forment, passant ainsi de l'état de "particule neutre" à celui "d'ion positif". Or ces électrons sont "libres", c-à-d potentiellement mobiles (notion de "nuage" d'électrons). Lorsque nous avons étudié la loi d'Ohm V = R * I (261), nous avons vu que cette mobilité est orientée en un courant, en appliquant une différence de potentielle entre les deux extrémités d'un conducteur. Quant au fil électrique, il contient autant de charges positives que négatives, de sorte que les forces qu'elles subissent sous l'effet du champ électrique s'annulent. Ainsi dans le schéma ci-dessous, les charges positives que sont les ions génèrent un champ extraverti, tandis que les charges négatives génèrent un champ intraverti (cf. supra #champ-electrique). Ainsi un fil qui conduit l'électricité est un corps électriquement neutre.
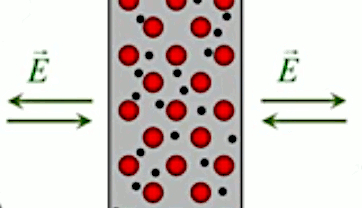
Un conducteur est composé d'ions positifs (en rouge) qui génèrent un champ extraverti, et de leurs électrons libres (en noir) qui génèrent un champ intraverti.
En montrant que le courant fait apparaître un champ magnétique, Ampère rompt avec l'idée selon laquelle la source du champ magnétique, ce serait un monopôle magnétique. Non, dit Ampère, la source du champ magnétique ce sont des charges électriques ... en mouvement !
Champ
vs force
Ça c'est pour le champ magnétique. Maintenant, comment interpréter, de façon moderne, l'origine de la force magnétique ?
Pour simplifier le raisonnement qui suit, on va supposer ici que les électrons sont positifs, comme nous l'avions fait dans le développement de la loi d'Ohm.
Reprenons le schéma de notre système. Le fil dont le courant va vers le haut se trouve dans la partie droite du champ de vision de l'observateur-chien. Celui-ci, grâce à ses super-lunettes, voit les vecteurs-champ des lignes de champ magnétique alentours, orientés dans sa direction (cf. pointes de flèche bleues).
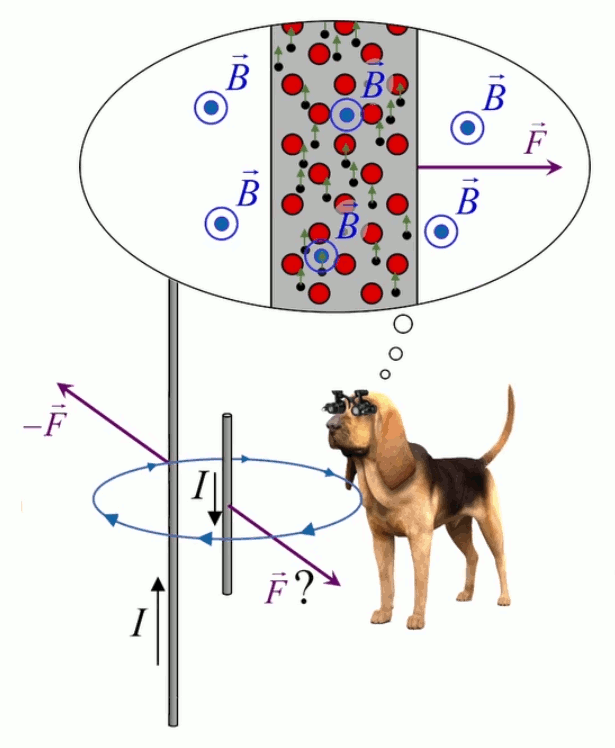
La bulle représente la vision, par l'observateurs-chien, de l'axe dont le courant va vers le haut (gauche sur le schéma, mais à droite pour le chien).
La réponse d'Ampère à la question posée est alors claire : dès lors que cette force magnétique est due aux mouvement des électrons, ce sont ces mêmes électrons qui subissent la force magnétique. Les électrons de la bulle du schéma ci-dessus sont ainsi tirés vers la droite, et partant, le fil aussi. Le même type de raisonnement s'applique au fil de gauche (dont le courant est opposé), de sorte que l'on obtient l'explication de leur écartement, exposé dans la vidéo.
Ampère a ainsi découvert la nature fondamentale de la force magnétique. Elle ne s'exerce pas sur des monopôles magnétiques, mais sur des charges électriques ... en mouvement. C'est la charge électrique en mouvement qui est à la fois responsable du champ magnétique, et sensible à ce même champ (c-à-d qui subira la force magnétique) !
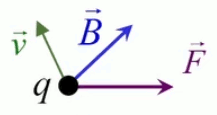
Le champ magnétique B→ est provoqué non par un monopôle magnétique qM mais par un courant (de vecteur vitesse v→) de charges électriques q.
Et, contrairement à l'interaction électrique, la direction de cette force n'est pas celle de son champ, car c'est une force radiale, alors que le champ est transverse !
N'oublions pas qu'à cette époque, la notion de champ – notamment en tant que matérialité physique – n'existe pas encore. Ce que représente ici le vecteur B→, c'est simplement la direction prise par l'aiguille aimantée.
Résumons ce que nous avons vu dans cette vidéo :
dans B→ = kM * I / r * 1→⊥ (284) le courant électrique I est au champ magnétique B→ (qui est perpendiculaire à la force)
ce que
dans E→ = kC * q / r 2 * 1r→ (207), la charge q est au champ électrique E→ (qui est parallèle à la force)
Autrement dit, de même que la charge électrique génère et subit le champ électrique, le courant électrique génère et subit le champ magnétique.
Enfin, alors que la force électrique est simplement le produit de la charge par le champ, on devine que la loi de force magnétique sera plus complexe ...
Formule d'Ampère
Dans la vidéo précédente, nous avons vu que deux fils parallèles véhiculant deux courants de sens opposés subissent des forces d'interaction répulsives. Cette expérience confirme l'intuition qu'avait eue Ampère, qu'un courant génère non seulement un champ magnétique, mais est aussi sensible au champ magnétique. Ainsi dans cette expérience, chaque courant est plongé dans le champ magnétique généré par l'autre courant.
Dans la présente vidéo, on va caractériser la force d'interaction magnétique, en fonction des paramètres des deux courants impliqués dans ces forces. Cela nous conduira à la formule d'Ampère.
Pour ce faire, nous allons étudier la force exercée sur le fil de droite, due au champ magnétique dans lequel il est plongé, et qui est généré par le fil de gauche. La partie droite du schéma suivant montre le point de vue d'un observateur situé au-dessus du système. Le sens du courant est indiqué par les symboles "pointe de flèche" (à gauche, qui sort du plan de l'image) et "plume de flèche" (à droite, qui rentre dans le plan de l'image).
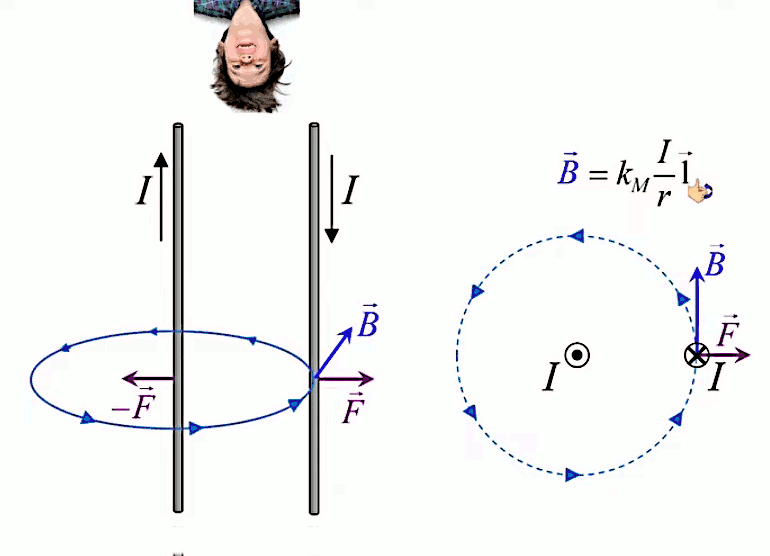
Le champs magnétique B→ est donné par la formule de Biot et Savart B→ = kM * I / r * 1→⊥ (284), liée au courant de gauche. Son sens est identifiable par la règle de la main droite : en plaçant le pouce dans la direction du courant, le sens de repliement des doigt indique alors celui du champ magnétique. Ainsi, sur le fil de droite, il est dirigé vers "le haut" (selon la partie droite du schéma).
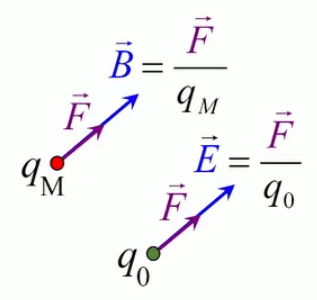
Si l'on considère que le champ magnétique s'exerce sur des charges magnétiques plutôt que sur des courants électriques, on retrouve alors un structure géométrique identique à celle du champ électrique.
Quant à la force exercée sur le fil de droite, elle est répulsive et radiale. Étant radiale, elle n'est pas parallèle au champ magnétique. Sa relation avec le champ magnétique est donc de nature différente de l'extrapolation faite par Coulomb à partir de la relation entre champ et force électrique, et qu'il avait formulée par F→ = qM * B→ (282), considérant le cas d'une charge magnétique qM. Or dans le présent système expérimental, qui concerne non pas une charge magnétique, mais un courant électrique, le champ magnétique semble avoir perdu son statut de champ de force. Cette complexité du champ électromagnétique est due au fait que son objet est non plus une charge mais un courant électrique. Alors que la charge peut être mathématiquement associée à un point, de sorte que l'on peut lui associer un scalaire (c-à-d un nombre) représentant cette charge ⇒ en divisant la force par la charge, on obtient la valeur du champ électrique : E→ = F→ / q0 (206).
Règle de la
main droite
Dans le cas de notre système magnétique, le courant est bien associé à un nombre (son intensité), mais il est en outre caractérisé par un sens, ce qui en fait un vecteur. Or nous avons vu que l'on ne peut diviser par un vecteur (cf. geometrie#proprietes-produit-scalaire). Dès lors, comment va-t-on mesurer le champ magnétique ? Les mathématiques du champ magnétique seront donc nécessairement plus complexes que celles du champ électrique. Ainsi le système associé au point représenté sur le fil de droite est composé de trois vecteurs.
Pour nous familiariser avec cette complexité, nous allons étudier la force subie par le courant de gauche. L'expérience nous a montré que cette force est répulsive, c-à-d opposée à celle subie par le courant de droite, de sorte que ce système obéit à la troisième loi de Newton (169) .
Pour identifier le sens de la force électromagnétique F agissant sur un courant électrique I0 plongé dans un champ magnétique B, nous allons appliquer une règle de la main droite spécifique : si les doigts sont placés dans le sens du courant, avec la paume tournée dans le sens du champ, alors le pouce indique le sens de la force.
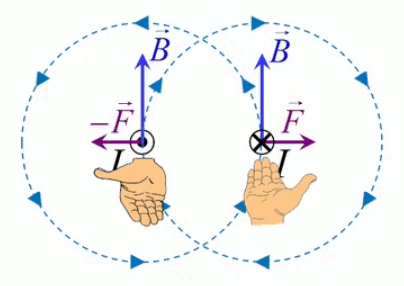
N.d.A. Les deux règles de la main droite
Nous avons donc une interaction entre :
- un courant électrique rectiligne, caractérisé par une direction et un sens ;
- un champ magnétique (dont la direction n'est pas nécessairement parallèle à celle de la force qu'il exerce sur le courant).
L'identification des sens de cette interaction se fait au moyen de deux règles de la main droite :
- sens du champ généré par un courant rectiligne (I) :
sens du pouce ≡ sens du courant ;
⇒
sens de repliement des doigts ≡ sens du champ - sens de la force électromagnétique exercée sur un courant (I0) par un courant parallèle de sens opposé :
- sens des doigts ≡ sens du courant I0 ;
- et paume vers sens du champ.
sens du pouce ≡ sens de la force électromagnétique
... ou bien règle du bonhomme d'Ampère (plus intuitive) :- tête ≡ pointe de flèche du courant I0 ;
- et face vers sens du champ.
sens du bras gauche ≡ sens de la force électromagnétique
Maintenant que nous maîtrisons la règle de la main droite, nous allons pouvoir caractériser les différents paramètres de notre système expérimental, ce qui nous conduira à établir la formule d'Ampère.
Sens du
courant
Un premier paramètre est le sens du courant. Nous avons vu plus haut que deux courants de sens opposés génèrent des forces répulsives. Qu'en est-il de courants de même sens ? : quelle sera la nature de la force d'interaction ? La lectrice est invitée à tester sa maîtrise de la règle de la main droite, en vérifiant dans l'animation ci-contre que, les courants étant de même sens, les champs sont alors opposés, et les forces attractives.
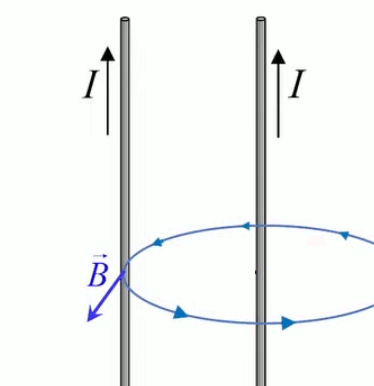
Conclusion : deux courants de même sens s'attirent, tandis que deux courants de sens opposés se repoussent.
Configuration
du système
Revenons à un système avec deux courants opposés, et intéressons-nous à un second paramètre : la longueur du courant. Mais comment peut-on déterminer la longueur d'un courant électrique ? En principe, la longueur du courant, c'est celle de la boucle qui part et revient à la source de tension.
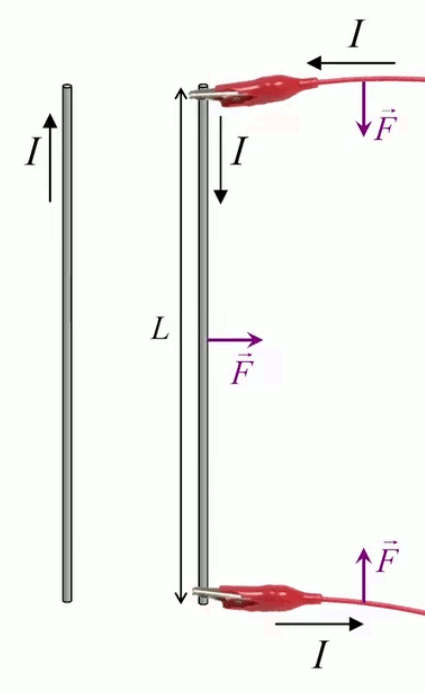
Cependant, si l'on oriente les deux fils de cette boucle, perpendiculairement à notre système de deux courants électriques parallèles, on peut montrer que la force qu'ils subissent est compressive. En effet, dans le schéma supra, le fil du dessus, étant soumis au champ rentrant (dans le plan de l'image) émis par le fil de gauche, subit une force le tirant vers le bas (vérifier avec la main droite, doigts dans le sens du courant vers le système, et paume orientée dans le sens rentrant dans le plan de l'image ⇒ le pouce est bien orienté vers le bas). Et pour la mêle raison, le fils du bas, dont le courant est opposé à celui du haut, tout en étant soumis au même champ magnétique rentrant, est logiquement tiré vers le haut. Au total le fil vertical de droite va donc subir une force de compression. Mais celle-ci n'aura pas d'impact sur la force horizontale exercée sur le fil vertical.
Ainsi la partie du fil vertical située entre les deux pinces peut être qualifié "d'élément de courant" (caractérisé par un courant I et une longueur L), de sortes que les deux fils conducteurs reliant notre système à la source de tension peuvent être ignorés.
Il reste cependant un autre problème expérimental à neutraliser : le fil de gauche (à l'origine du champ magnétique à l'origine de la force exercée sur le fil de droite) est perturbé par les fils conducteurs qui le relient à sa source de potentiel. Ces fils génère un champs (sortant du plan de l'image) qui va exercer des forces attractives sur le fil de gauche (vérifier avec la main droite, doigts vers le bas, et paume orientée dans le sens sortant ⇒ le pouce est bien orienté vers la gauche).
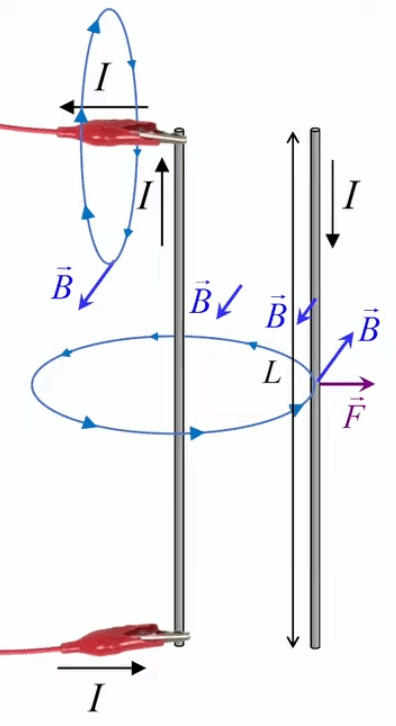
Pour neutraliser ce phénomène, il suffit cependant d'utiliser pour le fil de gauche une distance entre les fils de connexion suffisamment grande pour que le champ qu'il génère soit négligeable dans l'environnement proche du fil de droite (rappel : la formule de Biot et Savart B→ = kM * I / r * 1→⊥ (284) nous dit que l'intensité du champs diminue "par 1 sur r").
r
Dans ces conditions expérimentales, on pourra alors utiliser telle quelle la formule de Biot et Savart pour calculer l'effet de la distance r entre les deux fils verticaux, sur la force subie par le fil de droite. Et comme ces deux fils sont parallèles, le champ entourant le fil de droite y a partout la même intensité, de sorte que l'on pourra faire une correspondance entre le champ et la force.
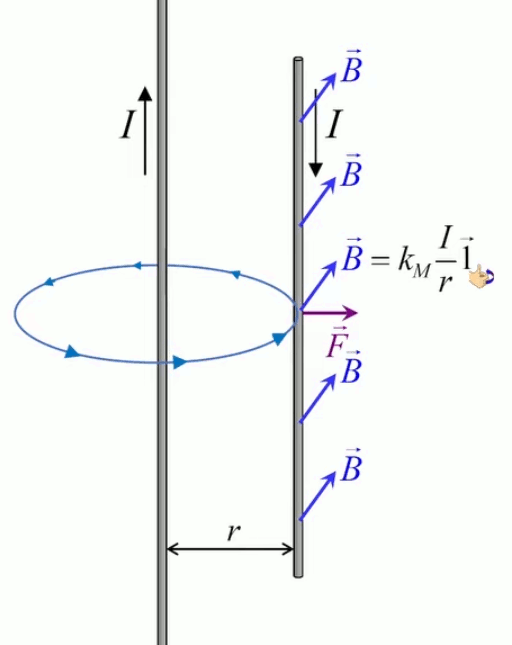
Cependant, nous avons vu que l'objet physique considéré dans la formule de Biot et Savart, c'est un monopôle magnétique (cf. supra #formule-Biot-Savart). Ampère va montrer expérimentalement que la loi en 1/r de la formule de Biot et Savart B→ = kM * I / r * 1→⊥ (284) s'applique également au cas d'un courant électrique (cf animation ci-contre).
Le premier élément de la formule d'Ampère est donc F ∝ 1 / r.
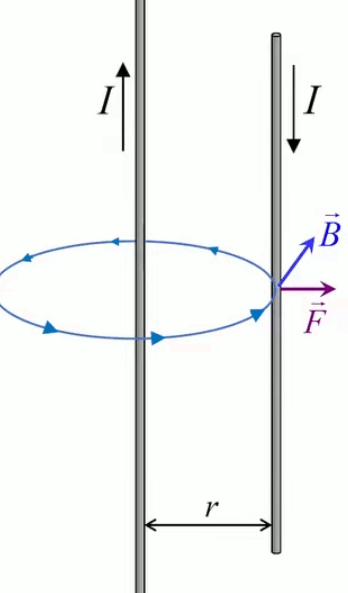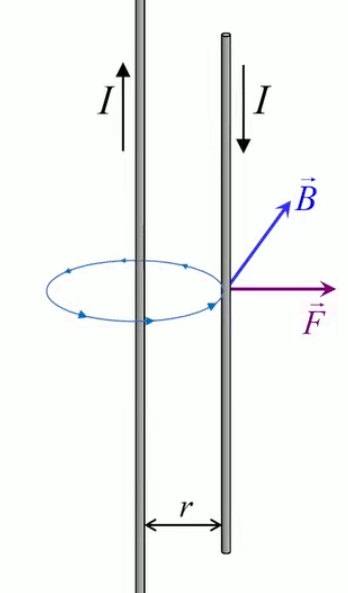
I
Passons maintenant à un second paramètre de la formule de Biot et Savart : le courant. N.B. : il s'agit du courant qui est la source du champ (fil de gauche), et non celui soumis à ce champs (fil de droite). Ce dernier est d'ailleurs noté I0 et appelé "courant d'essai", par analogie avec la charge d'essai q0 dans la formule de Coulomb FC = kC * q * q0 / r 2 (202) (PS : on notera la différence : 1/r pour la force magnétique, 1/r2 pour la force électrique).
L'expérimentation montre que, à nouveau à l'instar de la formule de Biot et Savart, il y a proportionnalité entre F et I, même en considérant un courant électrique plutôt qu'un monopôle. La formule d'Ampère devient donc F ∝ I / r.
L
Passons maintenant au troisième paramètre : la longueur de notre élément de courant. La force exercée sur le fil de droite est également distribuée le long de cet élément (notion de "force distribuée"), puisque le courant subit le même champ magnétique sur toute sa longueur, (chaque portion de courant subit la même force).
La formule d'Ampère devient alors F ∝ I / r * L
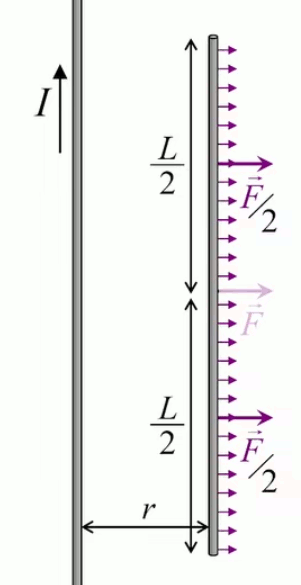
I0
Venons-enfin au dernier paramètre, le courant d'essai : I0. Par expérience de pensée, dédoublons le fil de droite, et collons ensemble ces deux fils jumeaux. L'ensemble qu'ils forment alors subit donc deux fois la force F, et véhicule un courant égal à 2*I0. Ainsi lorsqu'on multiplie le courant par un facteur n, on multiplie la force par le même facteur n.
Formule
d'Ampère
La version finale de la formule d'Ampère est alors
FM = kM * I / r * I0 * L
où la constante kM traduit la proportionnalité.
Interprétation. Le champ magnétique est causé par des courants électriques, et ce sont les courants électriques, sensibles au champs magnétiques, qui provoquent cette force. L'élément de courant, caractérisé par la grandeur I0 * L, subit une force FM lorsqu'il est plongé dans le (champ émis par) le courant I, situé à la distance r.
Notons que cette formule est en fait une version très simplifiée de la formule d'Ampère, correspondant à des fils parallèles, et dont un est d'extension infinie. La véritable formule d'Ampère est générale, s'appliquant à des deux courants de longueurs limitées et orientés dans n'importe quelles directions. Cette dernière généralité requiert d'introduire trois angles dans la formalisation. Cette approche, dite électrodynamique a cependant été remplacée par un autre formalisme, celui de la théorie moderne de l'électromagnétisme.
Constante de force magnétique : définition de l’Ampère
Il y a un parallèle évident entre la formule de la force magnétique d'Ampère FM = kM * I / r * I0 * L (285) et la formule de la force électrique de Coulomb FE = k0 * q * q0 / r 2 (202) :
- constantes de force électrique (k0) vs magnétique (kM) ;
- charge d'essai (q0) vs courant d'essai (I0 * L) ;
- effet du paramètre distance : 1/r2 vs 1/r.
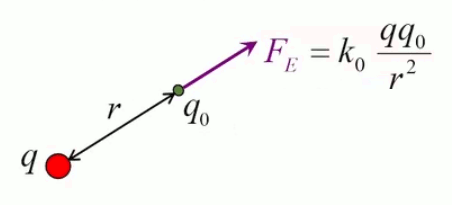
Force électrique de Coulomb
Pour évaluer la valeur de la constante de force magnétique kM, il suffit de l'isoler dans un membre :
FM = kM * I / r * I0 * L ⇔
kM = FM * r / I / I0 / L ⇒
on attribue ensuite des valeurs quelconques à r, I, I0 et L, par exemple :
• r = L = 1 m ;
• I = I0 = 1 A = 1 C/s ;
⇒ on mesure expérimentalement la valeur correspondante de F (par exemple au moyen de la balance à torsion de Coulomb) ⇒ on obtient :
FM = 2 10-7 N ⇒
on calcule la valeur de la constante de force magnetique kM à partir de l'égalité précédente :
kM = 2 10-7 N * 1m / 1A / 1A / 1m = 2 10-7 N / A2
Or, nous avons vu que kC = 8,99 * 109 N * m2 / C2 (203), qui est donc d'un ordre de grandeur plus de 16 fois supérieur à la constante de force magnétique !
Cette énorme différence se répercute évidemment sur les forces électrique et magnétique, calculées pour des valeurs unitaires des paramètres. Ainsi la force électrique correspondant aux valeurs de paramètres :
• q = q0 = 1 C
• r = 1 m
vaut : FE = 8,99*109 N, soit près de 9 milliards de N, c-à-d environ 1 milliard de kilogrammes-force (cf. /dynamique#force), ce qui est énorme !
Comparée à la force électrique, la force magnétique et donc négligeable (16 ordres de grandeurs de différence).
Une autre caractéristique notable de la formule d'Ampère est la valeur entière de sa constante kM : 2 "tour rond" 10-7. Ce fait étonnant – étant donné la nature généralement non entière des constantes universelles – est du au fait que l'ampère est défini sur base de cette valeur calculée au moyen de la formule d'Ampère. En effet, le courant de 1A, c'est le courant qui, dans cette configuration unitaire, produit une force de 2 10-7 N : « 1 ampère (ou 1 C/s) est la vitesse du courant qui – circulant dans deux fils, l'un de 1 mètre, l'autre de longueur extensible à l'infini, les deux espacés de 1 mètre – correspond à une force de 2 10-7 N exercée sur le fil de 1 mètre ».
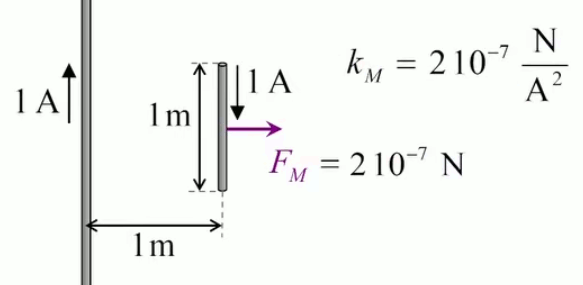
Système expérimental de définition de l'ampère.
Ce choix arbitraire concernant la définition de l'ampère, exprime le fait que cette unité est d'ampleur considérable. Dès lors que l'ampère est défini avant le coulomb, la relation entre ces deux unités devrait plutôt s'écrire C = A * s : un débit de charge d'1A pendant 1 seconde correspond à une accumulation de charges d'une valeur de 1 C. Or, 1 coulomb, c'est une charge gigantesque ! Ainsi, si pendant seulement une seconde, l'on charge les deux boules du schéma ci-dessous par un courant de 1 A, on obtiendra une charge d'un coulomb dans chacune des ces boules (que l'on appelle accumulateurs électrostatiques). Or, nous venons de voir que ce système correspond à une force de près de 1 milliard de kilogrammes-force. C'est plus que la force nécessaire pour soulever un porte-avion à pleine charge (c-à-d rempli avec équipage et équipements complets) !
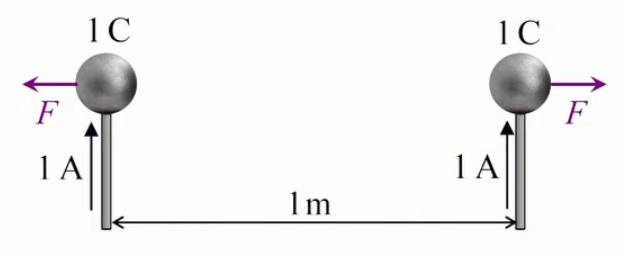
Et pourtant, 1 Ampère, on peut l'atteindre avec un simple fer à repasser ! Cette contradiction entre la facilité d'observer un courant de 1 A et la gigantesque vitesse d'accumulation de charges qu'il permet d'injecter dans un accumulateur, n'est qu'apparente. En effet, ce 1 A correspond à un transfert de charge dans un fil conducteur, qui est un objet neutre (il contient autant de charges positives que négatives), de sorte qu'il n'y a pas de champ électrique, donc pas de forces pour s'opposer au transfert d'une quantité de charges de 1 coulomb au travers de la structure cristalline du conducteur. Par contre, dans les deux boules métalliques de notre système, le courant y accumule des charges de sorte que celles-ci deviennent beaucoup plus nombreuses que le nombre de protons, provoquant des tensions croissantes par les forces répulsives entre électrons. Ainsi, sur des boules de la taille de l'illustration ci-dessus, ces tensions provoqueront des arcs électriques (expulsions d'électrons) bien avant d'atteindre le 1 C de charges.
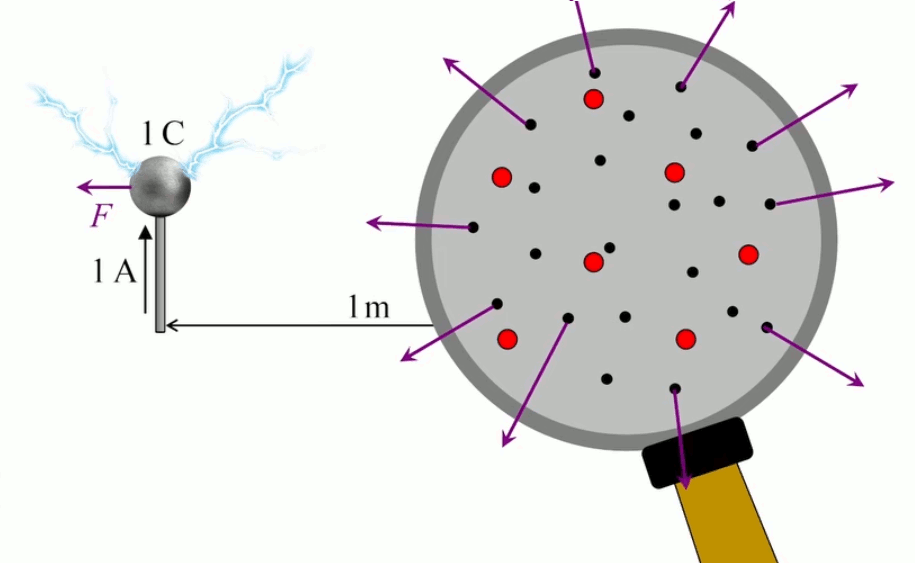
Revenons enfin à la définition de l'ampère. On entend parfois dire que « l'ampère est le courant qui, circulant dans deux fils de 1 mètre de longueur et espacés de 1 mètre, correspond à une force de 2 10-7 N ». Or cette affirmation est incorrecte. En effet, si le fil de gauche de notre système expérimental n'est pas d'extension infinie, alors le champ baignant le fil de droite n'y sera plus homogène, son intensité diminuant du centre vers les extrêmes, de sorte que la force qu'il subira sera inférieure à 2 10-7 N.
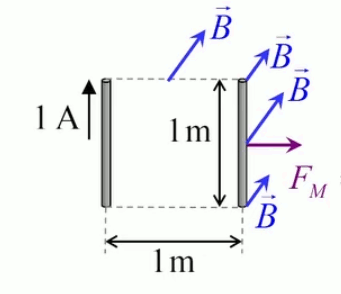
Il faudrait donc rapprocher suffisamment les deux fils (par exemple à 1 cm), afin que la réduction du champ soit limitée à ses extrémités et d'ampleur négligeable, de sorte qu'il y aurait quasi homogénéité sur toute sa longueur de 1 mètre. Mais dans ces conditions, la valeur de la force est augmentée d'un facteur 100 puisque r apparaît au dénominateur de la formule d'Ampère FM = kM * I / r * I0 * L (285).
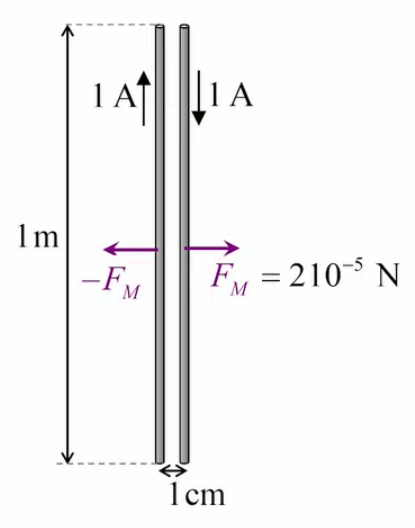
L'affirmation incorrecte énoncée plus haute devrait donc être remplacée par « 1 ampère est le courant qui, circulant dans deux fils de 1 mètre de longueur et espacés de 1 cm, correspond à une force de 2 10-5 N ».
Qu’est ce qu’un aimant selon Ampère ?
Décrire de façon complète et détaillée la théorie de l'origine du magnétisme dans la matière relève d'une micro-physique complexe, et qui par conséquent sort du cadre de ce cours. C'est pourquoi nous allons ici le faire sur base des seuls concepts élaborés par Ampère au début du 19° siècle.
Nous avons vu que le champ magnétique n'est pas créé par une charge magnétique mais par un courant électrique. Ampère en déduit-donc qu'un aimant est parcouru par un courant électrique permanent (NB : Ampère parlait alors de courant "moléculaire", car l'atome et ses électrons n'étaient pas encore connus).
Cependant, contrairement au courant dans un conducteur non magnétique, le courant d'un aimant n'est pas longitudinal mais transverse : c'est la notion de "courants de surface" ou encore "nappe de courants".
Le schéma suivant illustre une coupe transverse (tranche) de l'aimant illustré dans l'image précédente. Les lignes de champ générées par le courant sur les deux faces visibles sont déterminés par la règle de la main droite, correspondant à la formule de Biot et Savart B→ = kM * I / r * 1→⊥ (284).
Une coupe transversale (tranche) de l'aimant représenté dans l'image précédente.
Le schéma suivant compare les modèle d'Ampère (gauche) et Biot (droite). L'aimant y est vu du dessus. La différence se situe au niveau du sens du champs le long de l'aimant :
- modèle de Biot (droite) : du pôle positif/nord/rouge vers le pôle négatif/sud/noir ;
- modèle d'Ampère (gauche) : du pôle négatif/sud/noir vers le pôle positif/nord/rouge.
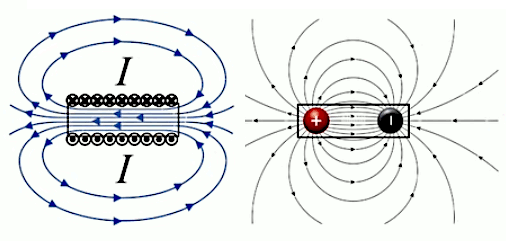
Gauche : aimant selon Ampère ; droite : aimant selon Biot.
Les instruments de mesure du champ magnétique dont nous disposons aujourd'hui confirment que c'est le modèle d'Ampère qui correspond à la réalité.
Notons que, dans le modèle d'Ampère, les lignes de champ forment une boucle fermée.
Quant au sens du courant de surface d'un aimant, on l'identifie facilement au moyen de la règle de la main droite : en pointant le pouce dans la direction du pôle nord de l'aimant, le sens de repliement des doigts indique le sens du courant (cf. supra #formule-Ampere).
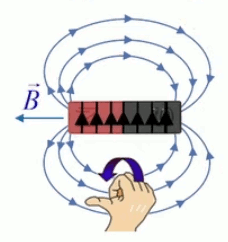
N.d.A. Les trois règles de la main droite
Nous avions déjà vu l'interaction entre :
- un courant électrique rectiligne, caractérisé par une direction et un sens ;
- un champ magnétique (dont la direction n'est pas nécessairement parallèle à celle de la force qu'il exerce sur le courant).
L'identification des sens de cette interaction se fait au moyen de deux règles de la main droite :
- sens du champ généré par un courant rectiligne (I) :
sens du pouce ≡ sens du courant ;
⇒
sens de repliement des doigts ≡ sens du champ - sens de la force électromagnétique exercée sur un courant (I0) par un courant parallèle de sens opposé :
- sens des doigts ≡ sens du courant I0 ;
- et paume vers sens du champ.
sens du pouce ≡ sens de la force électromagnétique
... ou bien règle du bonhomme d'Ampère (plus intuitive) :- tête ≡ pointe de flèche du courant I0 ;
- et face vers sens du champ.
sens du bras gauche ≡ sens de la force électromagnétique
Nous venons d'ajouter le cas de l'interaction avec un courant de surface :
- sens du champ généré par un courant circulaire (I) :
sens de repliement des doigts ≡ sens du courant
⇒
sens du pouce ≡ sens du champ
Interaction
Qu'en est-il de l'interaction entre aimants ? Comment expliquer – sur base de la thèse des courants de surface – que deux aimants s'attirent s'ils ont même orientation, et se repoussent dans le cas contraire. La réponse découle alors de la constatation expérimentale que deux courants opposés se repoussent tandis qu'ils s'attirent s'ils sont de même sens (cf. supra #formule-Ampere).
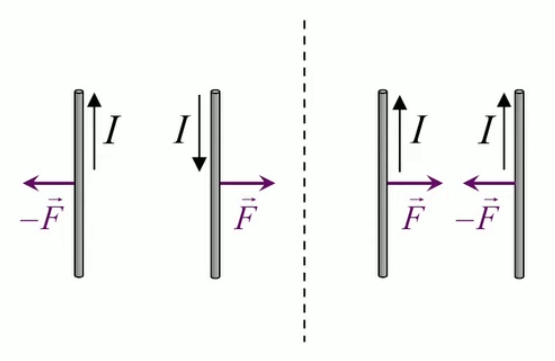
Le schéma suivant illustre que les courants de surface de deux aimants de même orientation s'attirent, à l'instar des deux fils de la partie droite du schéma ci-dessus, traversés par des courants électriques de même sens.
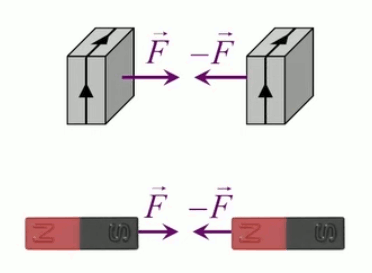
De même, pour deux aimants d'orientations opposées : leur courant étant de sens opposés, ils se repoussent donc.
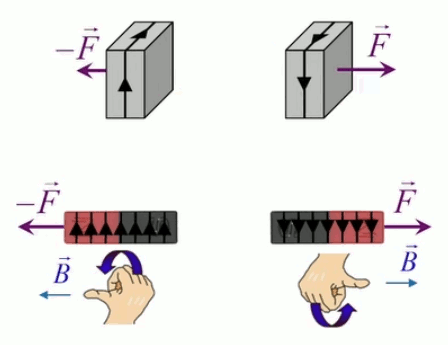
Ampère brise ainsi un consensus scientifique qui perdurait depuis cinq siècles. Il faudra cependant attendre un siècle de plus avant de pouvoir identifier les déterminants physiques de sa thèse : les atomes composant la matière, eux-mêmes composés d'un noyau autour duquel gravitent des électrons en mouvement. Ce sont ces électrons qui sont à l'origine du courant de surface des aimants. Dans la prochaine vidéo, nous verrons comment les électrons s'organisent pour créer les courants de surface des aimants.
Qu'est ce qui détermine le sens du champ magnétique ?
Qu'est ce qui détermine le sens du champ magnétique, toujours dans le même sens ? Cette asymétrie du phénomène magnétique ("pourquoi un sens plutôt que l'autre ?") est étonnante, dès lors que la source du phénomène, c-à-d le courant électrique, est symétrique ...
La règle de la main droite nous permet d'identifier ce sens : il suffit de diriger le pouce dans le sens du courant; de sorte que le sens de repliement des autres doigts indique celui du champ magnétique (cf. supra #orientation-champ-magnetique).
Cependant, identifier n'est pas expliquer. Nous allons voir que c'est l'hypothèse des courants de surface, qui permet d'expliquer le sens du champ magnétique.
Dans la section précédente, nous avons vu que le sens du courant de surface d'un aimant est indiqué par la règle de la main droite (pour un courant circulaire) : pouce dans sens du champ magnétique (pôle nord) ⇒ repliement des autres doigts dans le sens du courant de surface.
Supposons un aimant (≡ aiguille de boussole) plat dans une position quelconque par rapport à un conducteur rectiligne. Les pointes et plumes de flèche indiquent le sens du courant sur ses faces verticales (vues du dessus dans la bulle de pensée de la chauve-souris).
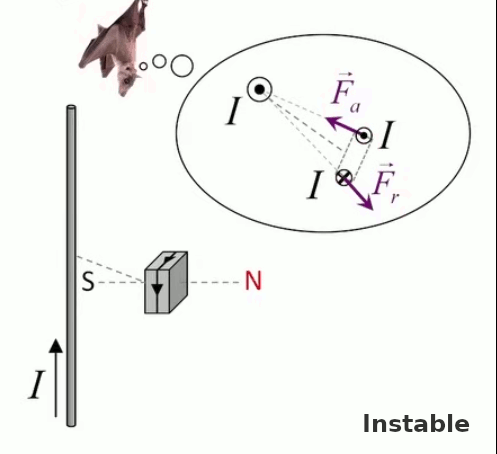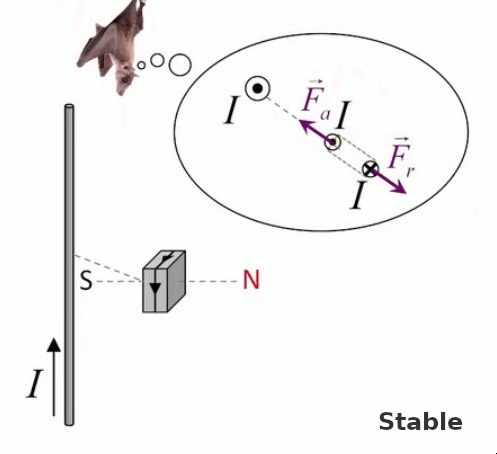
L'attraction (/répulsion) entre courants de sens identiques (/opposés) [cf. supra #formule-Ampere] a pour effet que cette position quelconque n'est pas stable, et qu'elle va nécessairement se stabiliser sur une position d'équilibre telle que ces deux forces s'annulent c-à-d telles que l'axe nord-sud de l'aimant est perpendiculaire au rayon qui émane du courant.
On détermine alors la direction et le sens du champ au moyen de la main droite : les doigts se replient dans le sens plongeant du courant, c-à-d vers l'extérieur, de sorte que le pouce indique alors la direction du pôle nord, c-à-d le sens du champ (PS : à ce stade de la présentation, on ne qualifie pas ce champ de magnétique, car Ampère ne postule par l'existence de charges magnétique, donc de forces, donc de champ magnétique non plus).
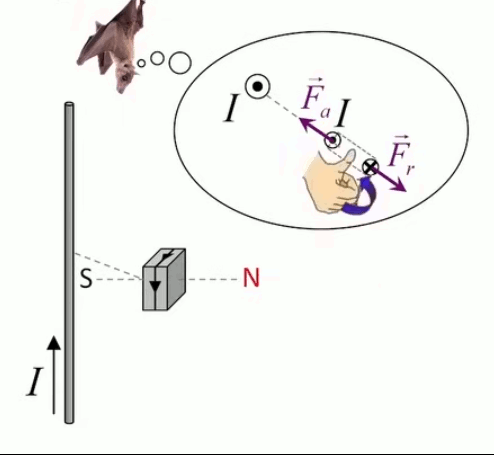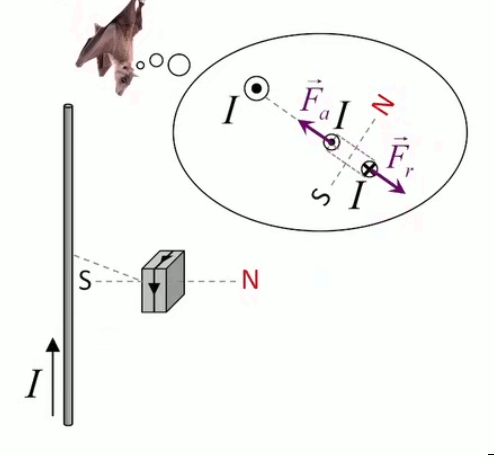
Ce qui détermine le sens du champ, ce ne sont donc pas des charges magnétique de signes opposés et situées aux extrémités de l'aimant (pôles nord et sud), mais le fait qu'en situation d'équilibre, le courant de sa face la plus rapprochée, correspond donc à une attraction, c-à-d un sens identique à celui du conducteur, de sorte que le courant de l'aimant remonte vers l'extérieur. La règle de la main droite pour un courant circulaire indique alors le sens du champ à l'équilibre, qui correspond à celui indiqué par la règle de la main droite pour le courant rectiligne (le conducteur).
Autrement dit, ce ne sont pas les force longitudinales attribuées aux pôles magnétiques qui s'exercent ici, mais des forces radiales (ou transverses) résultant des courants du conducteur et de l'aimant.
Ces principes valent également pour un aimant non plat. Les force radiales – attractives et répulsives – étant distribuées symétriquement, elles se ramènent, via leur somme, au cas de l'aimant plat.
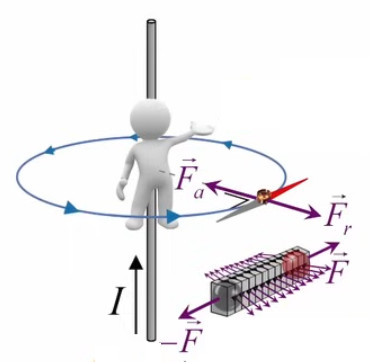
Le fait qu'Ampère faisait abstraction de la notion de champ magnétique, et ne considérait que des courants, ne posait pas problème tant que l'on restait dans le cadre de courants parallèles, mais conduisait à des développements mathématiques complexes lorsqu'il s'agissait d'étendre la théorie aux cas de courants de directions quelconques.
D'autre part, la notion de "champ de forces" (électriques), qui est utile pour représenter mathématiquement les forces entre charges électriques, ne permet pas d'étendre la théorie aux cas de courants de directions quelconques (c-à-d qui forment des angles entre eux).
Dans la prochaine vidéo nous verrons pourquoi on a malgré tout conservé la notion de champ magnétique – et cela malgré qu'on ne peut le considérer comme un champ de force dès lors qu'on a pas la preuve de l'existence de charges magnétiques.
Courants de surface et physique quantique
Comment expliquer la présence de courants électriques à la surface des aimants, alors qu'il n'y a pas de source apparente ?
Du macro
au micro
La réponse se trouve dans les atomes qui composent la matière. Ainsi l'atome d'hydrogène, le plus simple des atomes, est composé d'un proton et d'un électron (cf. supra #modele-atomique). L'électron (dont la masse est négligeable) est attiré par le proton, comme la lune est attirée par la Terre. Autre similitude : l'élément avec la masse la plus faible n'est pas seulement attiré, mais en outre il tourne de façon permanente autour de l'élément de masse supérieure. Cette permanence du "mouvement orbital" résulte de l'équilibre entre forces centripète et centrifuge.
Une différence réside dans le type de force centripète (attraction) :
- gravitationnelle au niveau macroscopique des planètes :
FG = G * m1 * m1 / r 2 (251) - électrique au niveau microscopique des particules "élémentaires" constitutives de la matière :
F(r) = kC * q1 * q2 / r 2 (202)
L'électron en mouvement crée donc un courant (électrique puisqu'il s'agit d'une chargée électrique). C'est la notion de "courant orbital". On comprend alors que celui-ci constitue la source des courants de surface des corps macroscopiques. Mais comment expliquer que ces courants se limitent à la surface ? La réponse réside dans le mode d'organisation des atomes composant la matière.
L'analogie du courant orbital des électrons autour du noyau atomique, avec le cycle orbital de la lune autour de la Terre, est une vision "naïve" (une interprétation) de la réalité microscopique, à l'aulne du modèle macroscopique de Bohr, dit "classique" (cf. supra #physique-atomique). Celui-ci n'est pas suffisant pour expliquer les propriétés complexes des "particules" "élémentaires" . On sait, depuis le début du 20° siècle, qu'il faut pour cela décrire l'atome dans le cadre de la mécanique quantique.
Fonction
d'onde
En mécanique quantique, l'électron est décrit comme un onde, c-à-d qu'en tant que particule, sa localisation ne peut être déterminée avec une précision supérieure à celle de la localisation du nuage électronique, qu'en termes probabilistes (c'est pourquoi la particule est dite "délocalisée").
N.d.A. Autrement dit, tant qu'on observe pas l'électron à un endroit déterminé, la seule chose qu'on sait sur sa possible (et unique) position c'est que les différentes possibilités sont équiprobables. Cette notion de délocalisation (ou incertitude de position) ne doit pas être confondue avec celles de (i) "non-localisation", ou intrication : corrélation instantanée de deux particules, même à de grandes distances, et (ii) "superposition" : phénomène par lequel une particule est dans plusieurs états à la fois (par exemple spin "up" et "down"). NB : aucune de ces trois notions n'implique celle d'ubiquité.
Le nuage électronique (notion physique) est exprimé mathématiquement par la "fonction d'onde" (N.d.A. : ses variables sont tout ou partie de : position, temps, spin, moment angulaire, énergie, ...).
Cette approche quantique soulève une première question : dès lors que la charge n'est plus localisée mais remplacée par un espace de positions (l'onde), et dès lors que celui-ci est stationnaire, l'électron n'est par conséquent plus soumis à une force centrifuge, de sorte que l'atome devrait s'effondrer sur lui-même, sous l'effet de la seule force centripète. La réponse à cette contradiction entre théorie et observation est que la fonction d'onde (le nuage électronique) contient une forme de rotation, et à laquelle correspond par conséquent une force centrifuge.
Pour faciliter la compréhension, nous allons illustrer nos propos dans un espace à seulement deux dimensions.
Mathématiquement, cette force centrifuge liée au nuage électronique s'exprime par le fait que la fonction d'onde est caractérisée par un "moment cinétique", grandeur proportionnelle à la masse et à la vitesse de l'électron (définition classique). Par conséquent, dès lors qu'il y a mouvement des électrons, il y a débit de charges au travers d'un plan, c-à-d un courant d'électrons.
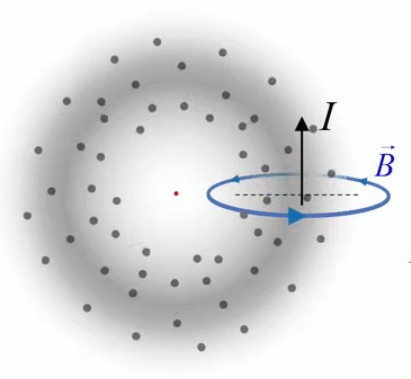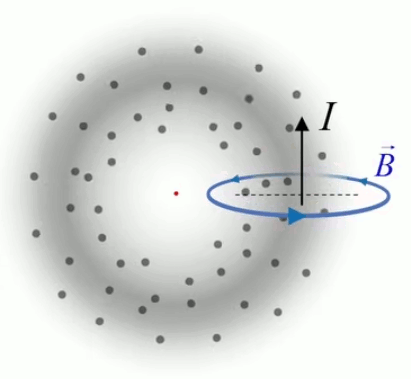
Voyez les électrons tourner dans le sens indiqué par la flèche.
Cependant, contrairement au courant de la pile de volta, qui est de dimension macroscopique, conductif (via la structure cristalline du conducteur) et temporaire (il disparaît lorsque le circuit est ouvert), le courant du nuage électronique est microscopique, orbital et permanent (inhérent à l'atome).
Le nuage électronique – la fonction d'onde, en terme mathématique – génère donc un champ magnétique.
Le sens de ce champ magnétique est déterminé par la même règle de la main droite (PS : on suppose que l'électron a une charge ... positive, afin de ne pas devoir chaque fois inverser la règle de la main droite). Dans le graphique ci-contre, pour avoir un idée de la visualisation en 3D, on passe de la vue "du haut" à la vue "de face" ⇒ on constate que la situation est comparable au champ magnétique de la Terre.
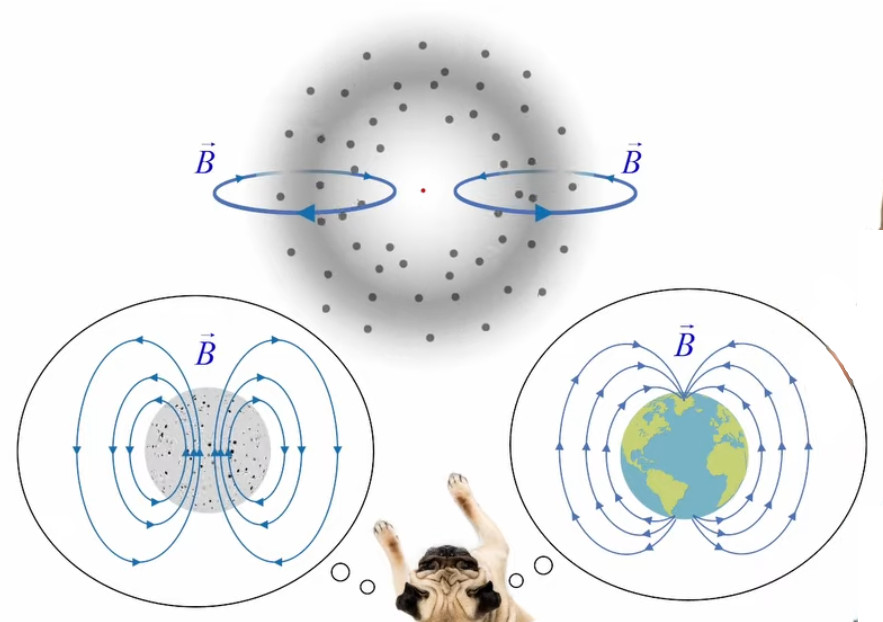
N.d.A. En haut, la vue du haut. En bas la vue de face, où un courant de surface perpendiculaire à l'axe nord-sud rentre sur le côté droit.
Au niveau de la Terre, le champ magnétique dipolaire est du à des mouvements de convection dans son noyau liquide, mais on retrouve bien la même notion de mouvement circulaire.
L'atome n'est donc pas seulement caractérisé par un "moment cinétique" (correspondant au courant électrique dans le nuage), mais également par un "moment magnétique", grandeur physique traduisant le module c-à-d l'intensité du champ magnétique (dipolaire) généré par ce courant.
Spin
Passons maintenant à un niveau de complexité supérieur, avec l'atome de fer (métal composant certains aimants), qui comprend un proton et plusieurs électrons. Nous avons vu que les électrons sont positionnés en couches composées de 2 électrons pour la première (la plus proche du noyau) et 8 par couche supplémentaire, sauf la dernière qui contient un nombre d'électrons inférieur ou égal à huit. (cf. supra /matiere#orbites-electroniques).
D'autre part, les électrons sont appariés, et circulent en sens opposés sur leur orbite. Par conséquent, lorsque le nombre total d'électrons est pair, la fonction d'onde globale est alors composée de deux flux d'électrons dont le débit net est nul (I=0), de sorte qu'il n'y a pas de champ (B→=0). Conclusion théorique : un atome ne génère pas de champ magnétique s'il est composé d'un nombre pair d'électrons.
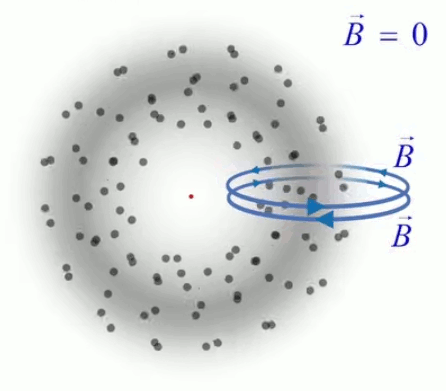
Cependant cette conclusion théorique ne correspond pas aux observations. En effet, le fer est composé d'un nombre pair d'électrons (26 en l'occurrence : cf. /matiere#tableau-periodique), et pourtant il génère bien un courant de surface.
Pour comprendre la signification de cette contradiction apparente, il faut pouvoir analyser la structure de l'électron. Celle-ci été été découverte en 1925, ce qui a donné naissance à la notion de "spin", qui est le moment cinétique intrinsèque des particules quantiques. Par "intrinsèque" on entend que le spin est une propriété purement quantique, c-à-d propre à cette échelle microscopique. Elle correspond, dans une interprétation classique (c-à-d macroscopique), à une rotation de l'électron sur lui-même.
N.d.A. Cette analogie avec une interprétation classique a pour but de maintenir la continuité du fil rouge dans approche vulgarisatrice. Cependant, elle ne correspond pas à la réalité. Le spin est "semblable à une sorte de moment cinétique", mais il ne peut pas être représenté comme une rotation spatiale de l'électron autour de son axe. C'est en cela que la notion de spin est dite intrinsèque à la physique quantique.
Nous allons montrer que ce mouvement rotatif des électrons, correspond donc à des courants, qui génèrent un champ magnétique. Ainsi l'électron génère non seulement un champ électrique (radial), mais également un champ magnétique (dipolaire). L'électron est donc caractérisé par un moment magnétique, ce qui peut être générateur du magnétisme dans la matière, puisque la matière est constituée d'électrons.
Couplage
spin-orbite
En raison de la délocalisation des électrons, leur propriété "rotative" exprimée par leur spin se retrouve au niveau du nuage. Ainsi d'une certaine manière, la fonction d'onde va posséder cette propriété de moment magnétique du spin. C'est la notion de "couplage spin-orbite" (très complexe au niveau calculatoire).
Mais pour montrer cela, il nous faut résoudre un nouveau problème théorique : lorsque deux électrons s'apparient, ils inversent leurs spins (c-à-d qu'ils adoptent des sens opposés), en vertu du principe physique "d'énergie la plus faible", par lequel tout corps tend naturellement vers un niveau d'énergie minimal (exemple de la chute d'un corps vers un état où son énergie gravitationnelle est minimale). En effet, l'opposition des spins correspond à l'état d'énergie le plus faible d'une paire d'électrons.
Donc, au total, on retombe théoriquement sur une fonction d'onde telle que son moment magnétique total est nul (ni orbital, ni de spin) :
- au niveau orbital, car les électrons appariés circulent sur leur orbite dans des sens opposés ;
- au niveau du spin, car les électrons appariés tournent sur eux-mêmes dans des sens opposés.

Et pourtant, l'aimant de fer génère bien un champ magnétique ! Comment compléter la théorie pour résoudre cette contradiction entre théorie et observations ?
L'explication réside dans le fait que le fer apparaît sous forme, non pas d'un unique atome, mais d'un groupe d'atomes. En l'occurrence, le fer s'organise spatialement sous la forme d'un "réseau à mailles cubiques centrées", dans lequel les électrons "collent" l'un à l'autre sous l'effet de l'interaction de leur couche de valence, c-à-d leur orbite la plus excentrée (cf. supra /matiere#orbites-electroniques).
Cette fois, le principe de minimisation de l'état énergétique correspond au phénomène par lequel les 2*2 électrons des deux couches de valence, adoptent spontanément le même spin que l'un deux (cf. schéma ci-contre), donc à l'opposé de l'appariement. Les 2*2 électrons tournent ainsi dans le même sens. Il en résulte que le spin total ("moment cinétique") de chacun des deux atomes de fer est non nul. Et via le couplage spin-orbite, cette état se répercute sur le nuage électronique de chaque atome de fer.
On retrouve donc un courant non nul, mais qui n'est plus de nature orbital, puisque les électrons continuent à tourner sur leurs orbites respectives dans des sens opposés. C'est un courant qui résulte du partage d'un même spin par les électrons de valence d'atomes connexes.
La délocalisation de l'électron a pour effet que ce courant se retrouve dans la fonction d'onde de chaque atome. Et il y a donc génération d'un champ magnétique, qui résulte de l'interaction avec un atome voisin. Ainsi tous les atomes du réseau du réseau tournent dans le même sens.
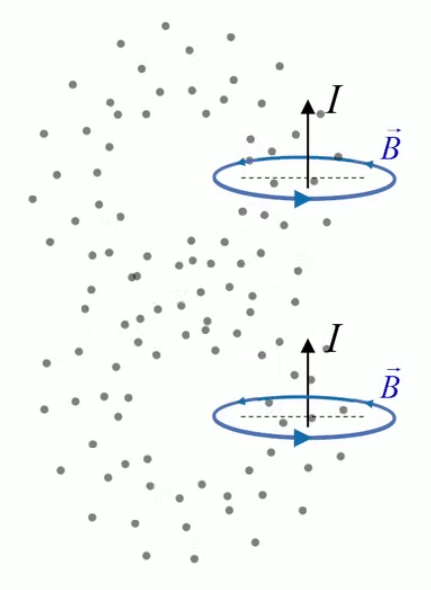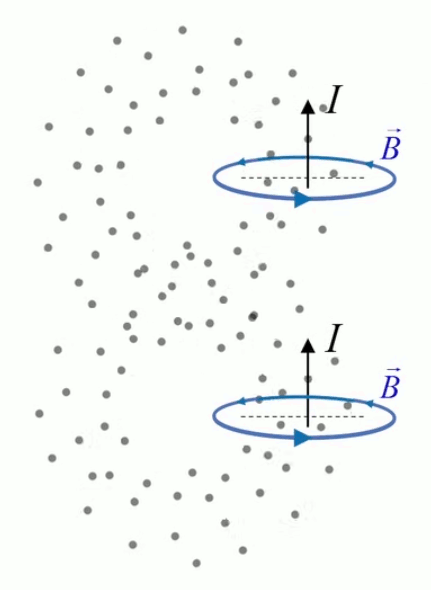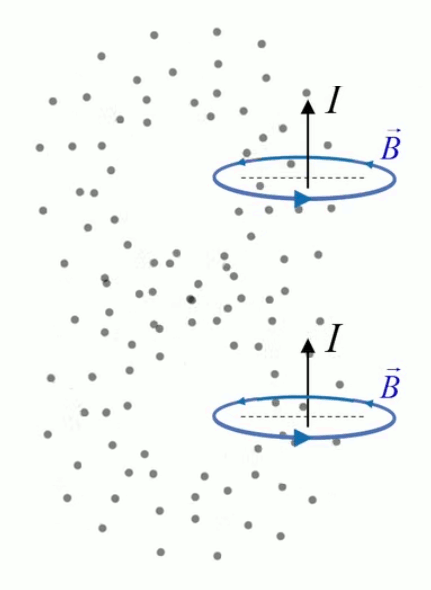
Voyez les électrons des deux atomes tourner dans le sens indiqué par la flèche.
Cependant si l'on mesure le courant entre deux atomes, on observe deux courants de sens opposés, et qui s'annulent donc : le courant dans la partie inférieure du nuage supérieur va de gauche à droite, tandis qu'il va de droite à gauche dans la partie supérieure du nuage inférieur.
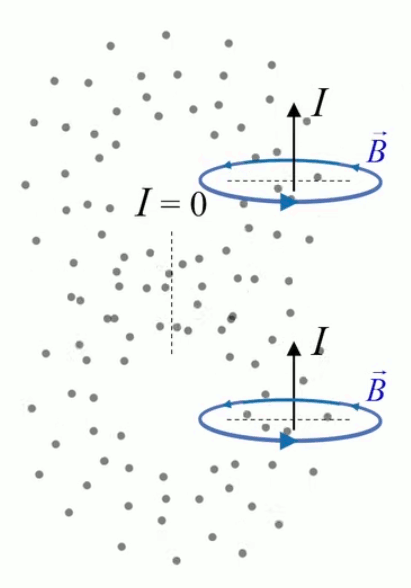
Il n'y a donc pas de source de champ magnétique entre les atomes.
Pour généraliser à plus de deux atomes, considérons une maille en 2D, carrée. Tous les atomes "tournent" donc dans le même sens puisque les spins partagent la même orientation, de sorte que leur moment magnétique est identique. On constate alors qu'il n'existe un courant qu'à la périphérie de cette maille.
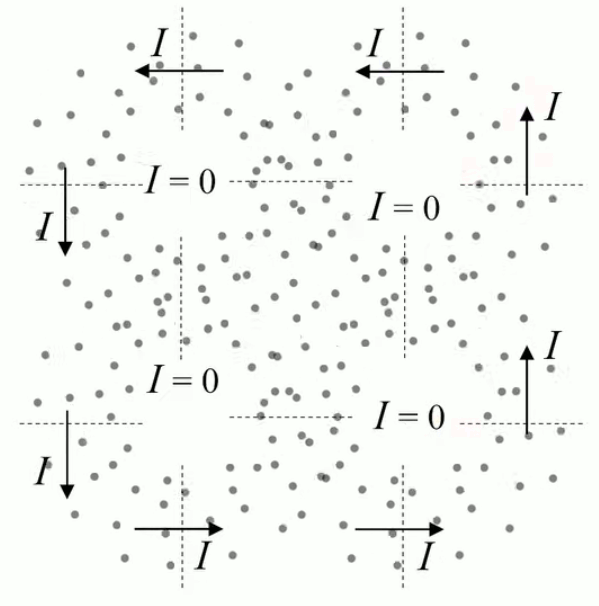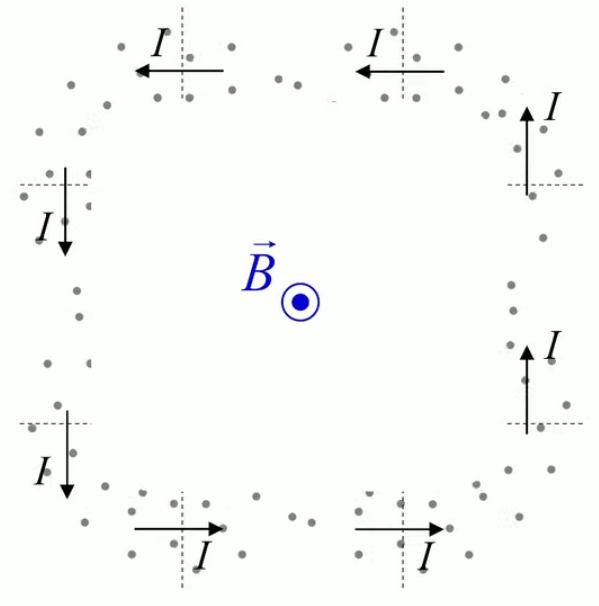
La règle de la main droite indique que la direction du champs sort du plan.
Et voilà, nous ainsi expliqué les courants de surface (certes de façon simpliste) ! Ils ont l'apparence de courants de conduction, mais ils n'en sont pas. Ce sont en réalité des courants orbitaux de spins.
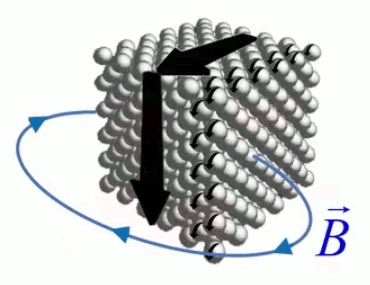
Pouce dans le sens du courant de surface (flèche noire) ⇒ le sens de repliement des doigts indique la direction du champ magnétique.
Il a fallu plus d'un siècle après Ampère avant de le découvrir. Depuis, on a découvert le même phénomène pour d'autres métaux que le fer : Cobalt (Co), Nickel (Ni), Néodyne (Ni), ou encore des alliages (métaux composites).
Le néodyme est très puissant car les couplages de spin sont très forts, et par conséquent les courants de surface, de l'ordre de centaines de milliers d'ampère (ils peuvent gravement blesser un doigt pris entre deux aimants, disponibles dans le commerce).
Résumé (N.d.A.)
Le champ magnétique des aimants est généré par le courant électrique qui circule à leur surface.
La source de ce courant, ce sont les électrons qui composent le nuage électronique de chacun des atomes constituant la matière. Au niveau microscopique des électrons, on considère qu'il y a non-localité des particules, c-à-d que celles-ci ont les propriétés d'une onde. Ainsi le nuage électronique est exprimé mathématiquement par une fonction d'onde, dont une variable est le spin des électrons ...
Le spin correspond à un moment cinétique, raison pour laquelle, les textes de vulgarisation font l'analogie (dans une interprétation classique c-à-d macroscopique) avec une rotation de l'électron sur lui-même. La transmission du moment cinétique du spin de chaque l'électron à la fonction d'onde est appelé couplage spin-orbite.
La mécanique du couplage spin-orbite est telle que le flux net de courant est nul entre les atomes, et ne subsiste donc qu'à la surface de l'aimant qu'ils constituent.
Ce courant de surface n'est donc pas conductif, mais résulte plutôt de la mécanique des spins.
Pourquoi a-t-on abandonné Ampère ?
Le début du 19° siècle est marqué par l'abandon progressif des théories d'Ampère.
Il avait mis un terme (temporaire) aux théories postulant l'existence d'un monopole magnétique, qui avaient constitué le consensus scientifique durant six siècles :
- 13° siècle : Pierre de Maricourt
- 16° siècle : William Gilbert, René Descarte
- 18° siècle : Charles-Augustin Coulomb
- 19° siècle : Jean-Baptiste Biot
Pour réfuter la pertinence du monopole magnétique, Ampère lui avait opposé deux arguments :
- ses expérimentations ont conduit à l'explication de la force magnétique comme force d'interaction entre courants électriques (et non pas entre monopôles magnétiques) ;
- les interactions entre aimants sont expliquées par l'action de courants de surface (et non de monopôles magnétiques).
Rappel : Ampère avait substitué le courant au monopôle afin de résoudre la violation du principe de conservation de l'énergie ("troisième loi de Newton") qu'implique le principe du monopôle (cf. supra #courant-champ-magnetique).
Sur base de ces deux éléments, Ampère a développé un formalisme mathématique, baptisé "théorie de l'électrodynamique", qui était tout à fait cohérente avec les expérimentations de l'époque.
Cependant, au même moment, Michael Faraday (qui connaissait les travaux d'Ampère) réalisa des expérimentations sur l'interaction entre magnétisme et électricité, et qu'il allait interpréter en revenant à la notion de monopôle magnétique !
Comme illustré ci-dessous, Farraday (qui était essentiellement un expérimentateur), en faisant mouvoir un aimant dans une bobine de fil de cuivre, constata l'apparition d'un courant électrique, c-à-d d'un différence de potentiel, et donc d'un champ électrique.
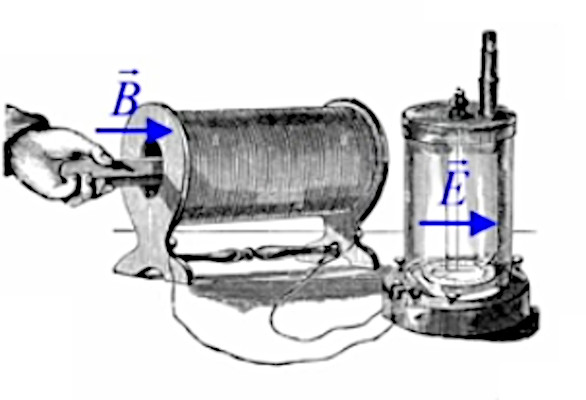
Pour expliquer ce phénomène, Farraday attribua au champ magnétique une réalité physique, alors que jusqu'alors le champ magnétique n'était qu'une notion géométrique, permettant de simplement décrire (et non pas d'expliquer) les observations expérimentales. Ainsi les lignes de force évoquées par Gilbert et Descartes n'avaient pour fonction que d'indiquer l'orientation de l'aiguille de la boussole, selon les différents points de l'espace où elle est placée. Mais pour Faraday, le champ magnétique serait véritablement une substance occupant l'espace environnant l'aimant de l'expérience. C'est le glissement de cette substance sur le fil de cuivre de la bobine qui expliquerait l'apparition d'un courant électrique dans le dispositif de droite.
Et cette "matérialité" du champ magnétique vaudrait également pour le champ électrique. L'intercation entre deux charges électriques ne serait donc pas une "simple" interaction à distance (comme on le supposait également pour la force de gravitation de Newton). Pour Faraday, s'il y a une interaction entre charge électriques, c'est parce qu'elles créent des champs électriques : si la charge électrique q du haut dans le schéma ci-dessous subit la force FE→, c'est parce que la charge q du bas génère un champ électrique E→, qui vient véritablement pousser la charge du haut.
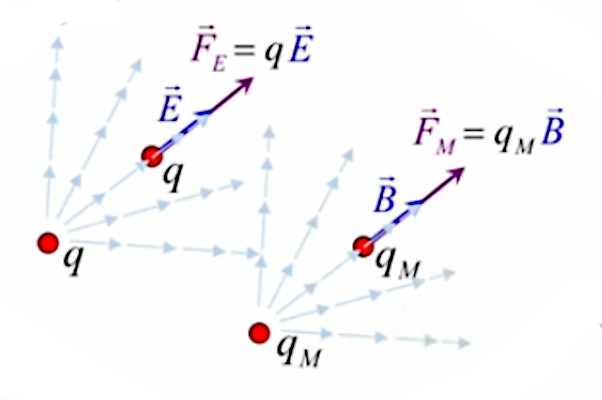
Selon Faraday, (i) les champs (électrique comme magnétique) ont une réalité physique, et (ii) le champ magnétique agit sur des particules magnétique (comme le champ électrique agit sur des particules électriques).
Farraday raisonne donc plus en terme de champs qu'en terme de forces ! C'est lui qui a introduit les notions de champs électrique et magnétique, de façon tout à fait parallèle. Ainsi le champ de force magnétique agit sur des particules magnétiques ... ce qui contredit frontalement la thèse d'Ampère selon laquelle la force magnétique agit sur des courants, et non des monopôles magnétiques.
Cette réhabilitation du monopôle magnétique va être renforcée par Maxwell, qui trente ans plus tard, vers 1860, va formaliser les travaux de Farraday pour construire la théorie de l'électromagnétisme, qui introduit la notion d'induction électromagnétique, phénomène par lequel le déplacement d'un champ magnétique provoque l'apparition d'un champ électrique.
L'apport mathématique de Maxwell a été facilité par la symétrie conceptuelle entre interaction électrique et interaction magnétique, illustrée par le schéma supra.
La théorie de l'électromagnétisme permet d'expliquer bien plus de faits expérimentaux que ne le pouvait la théorie de l'électrodynamique. Dans les séquences qui vont suivre on verra comment le champ magnétique de Faraday, bien que constituant un champ de force agissant sur les monopôles, peut être utilisé pour décrire l’interaction magnétique entre courants, découverte par Ampère.
Pourquoi le concept de champ ?
Pourquoi Faraday introduit-il la notion de champ magnétique – considéré comme un champ de forces agissant sur des charges magnétiques – alors que (i) on n'avait pas (et on a toujours pas) observé de charge/monopôle magnétique, et (ii) Ampère avait démontré que la force magnétique était une force d'interaction entre courants électriques, et non pas en entre charges magnétiques ?
Pour répondre à cette question, nous allons commencer, dans cette section, à préciser le concept de champ (électrique ou magnétique) tel qu'inventé par Faraday et Maxwell.
Rappelons qu'avant Faraday, la notion de champ (électrique comme magnétique) n'existait pas ! Ses prédécesseurs, à commencer par William Gilbert, parlaient de "lignes de force" pour indiquer la façon dont une aiguille de boussole s'oriente quand on la déplace dans l'environnement d'un objet magnétique. Dans les formalisations F→ = q0 * E→ (206) et F→ = qM * B→ (282), il n''était attribué aucune réalité physique aux notations E→ et B→. Il s'agissait seulement d'un formalisme mathématique visant à simplifier la notation.
Dans la forme vectorielle de la loi de Coulomb F→ = kC * q * q0 / r 2 * 1r→ (205), la force électrique est proportionnelle à la charge q0 qui subit la force. Pour simplifier la notation, on a alors regroupé tout ce qui n'est pas q0, sous la forme E→ = kC * q / r 2 * 1r→ ⇒ F→ = q0 * E→ (206), ce qui permet de définir mathématiquement le champ électrique par E→ = F→ / q0. Cependant, du point de vue physique, cela ne dit rien sur l'interaction entre les deux charge q et q0.
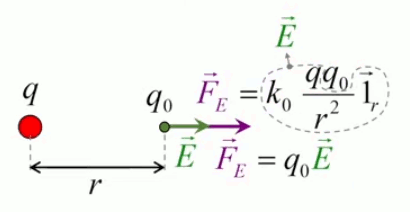
Autrement dit, avant Faraday, on supposait, suivant la théorie de Newton sur la force gravitationnelle f→ = - m * G * M / r 2 * 1→r (251), que, au niveau physique, il y a une action à distance entre les deux charges. Par "à distance", on entend que rien de matériel n'intervient entre celles-ci.
Comme l'illustre l'animation suivante, selon Newton, cette action à distance est instantanée. Ainsi, si la charge q est éloigné (augmentation de la double flèche noire) alors la force subie par q0 est immédiatement modifiée (diminution de la flèche mauve).
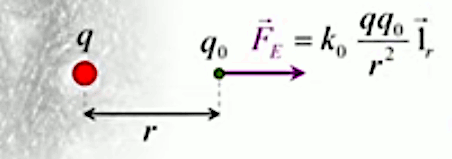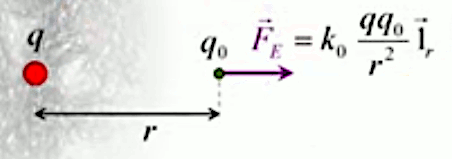
Interaction électrique (Coulomb) : à distance et instantanée
Cela vaut aussi bien pour l'interaction électrique de Coulomb (ci-dessus) que de l'interaction magnétique entre courants électrique d'Ampère (ci-dessous).
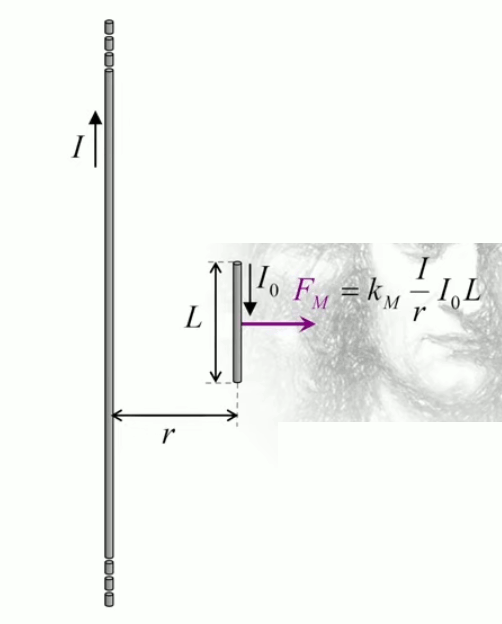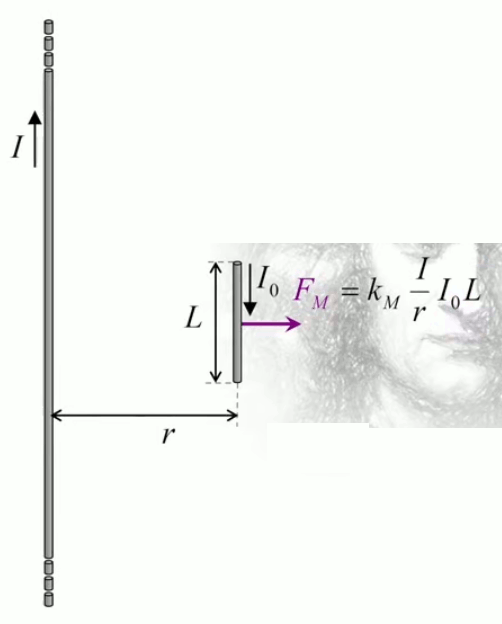
Interaction magnétique (Ampère) : à distance et instantanée
Mais tout va changer suite aux travaux expérimentaux de Faraday ...
L'expérence
de Faraday
L'animation suivante illustre l'expérience de Faraday. On y voit les lignes de champs magnétique émerger du pôle nord d'un aimant. Celui-ci est déplacé vers la droite devant une tige métallique (par exemple en cuivre). En passant à travers celle-ci, les lignes de champs y provoquent une accumulation de charges électriques positives à l'extrémité supérieure, et de charges négatives à l'extrémité inférieure. Et une fois que l'aimant est à nouveau immobile, les charges ont disparu. C'est donc le mouvement du champ magnétique qui fait apparaître les charges électriques dans la tige conductrice.
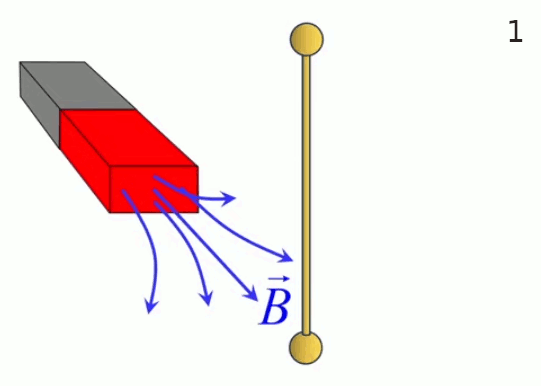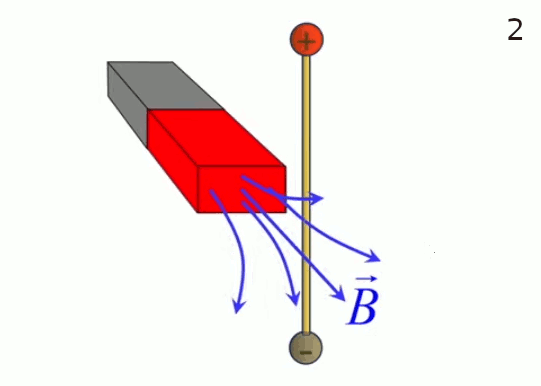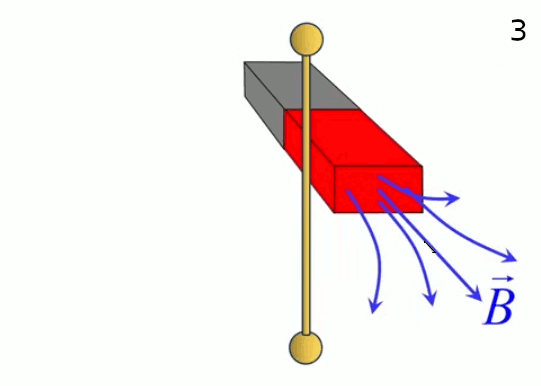
L'expérience de Faraday. Notez, dans l'étape 2/3, l'apparition des charges de signes opposés aux deux extrémité de la tige conductrice lorsque le champ traverse la tige, puis la disparition de ces charges lorsque le champ est passé au-delà de la tige.
Pour expliquer ce phénomène, Faraday se base sur la notion de courant électrique, qu'Ampère avait proposée en étudiant le magnétisme. Ampère avait proposé que dans tout matériaux conducteur il existe des particules (qu'il appelait "molécules") d'électricité (on sait aujourd'hui qu'il s'agit d'électrons). Faraday suppose donc que dans son expérience, le mouvement du champ magnétique aurait repoussé ces charges. Par conséquent, le champ magnétique joue un rôle équivalent à une charge, qui repousserait les charges de même signe contenue dans la tige, selon la loi de Coulomb F→ = kC * q * q0 / r 2 * 1r→ (205).
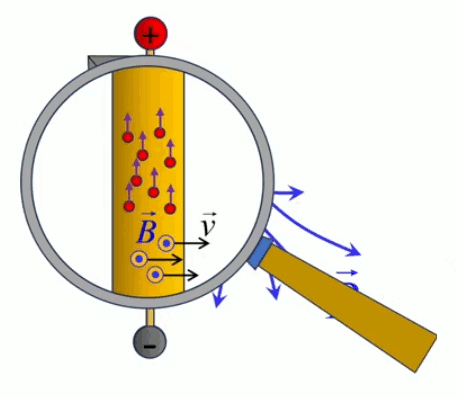
Le champ magnétique B→ se déplace vers la droite à vitesse v→, provoquant ainsi un courant de charges positives vers le haut.
Avec cette nouvelle interprétation, les "lignes de force magnétique" – notions qui n'avaient jusqu'alors qu'une signification simplement géométrique (informationnelle) – acquièrent une véritable nature physique, à l'instar de la charge électrique, dont le champ reproduit ici les effets. Le terme de "champ" inventé par Faraday exprime cette réalité physique des lignes de force magnétique. Le champ est une substance d'une nature étrange, qui passe à travers la tige de l'expérience, et ne suscite aucune sensation dans une main qui l'approche ...
La force magnétique ne s'exerce donc pas à distance. Le champ joue un rôle physique médiateur entre les charges magnétiques (partie inférieure du schéma suivant). Et Faraday étend ces suppositions aux cas des charges électriques : le champ préexiste à la charge q0, et quand celle-ci y est placée, une force est exercée sur elle (partie supérieure du schéma ci-dessous).
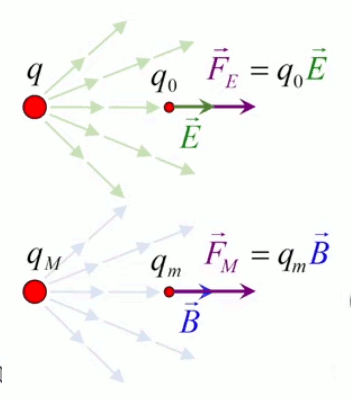
Induction
La grande surprise révélée par l'expérience de Faraday, c'est donc que le champ magnétique n'agit pas seulement sur des charges magnétiques, mais également sur des charges électriques. Et les forces que celles-ci subissent sont donc le signe que le champ magnétique (qui se dirige vers la droite) génère un champ électrique (qui se dirige vers le haut). C'est le phénomène d'induction électromagnétique.
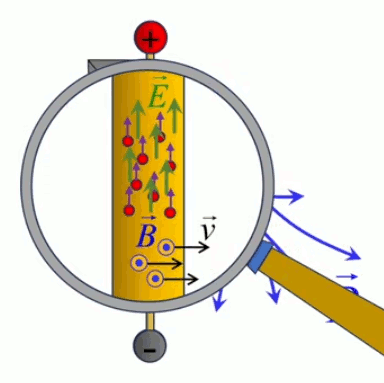
Induction électromagnétique : le champ magnétique B→ dirigé vers la droite génère le champ électrique E→ dirigé vers le haut.
Dans ce contexte de "matérialisation" des champs, il n'y a plus aucune raison de soutenir l'action à distance ni l'instantanéité de l'interaction. L'intermédiation du champ, implique une action "mécanique" (par exemple de type élastique) qui agit avec un certain temps de réponse, suite au mouvement qui l'a déclenché.
À partir de ce moment, le concept de champ (Faraday) va prendre le dessus sur celui de force (qui fonde la loi de gravitation de Newton), dans la réflexion des scientifiques. Faraday n'est cependant pas allé plus loin, cet expérimentateur est ce qu'on appelle un scientifique conceptuel. C'est Maxwell qui au début des années 1860 va proposer une modélisation mathématique, à partir de la notion de champ proposée par Faraday une trentaine d'années plus tôt. Les équations de Maxwell expriment, via les dérivées (cf. /algebre#derivee), l'effet du mouvement d'un type de champ (membres de droite) sur l'autre (membres de gauche).
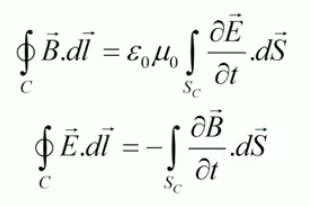
Équations de Maxwell
Cependant le B→ des deux équations ci-dessus est un champ de forces appliqué à une charge magnétique, alors qu'Ampère avait montré que la force magnétique apparaît entre courants électriques.
Or ces deux voies théoriques semblent incompatibles car, expérimentalement, elles correspondent à des directions différentes des forces (en l'occurrence, perpendiculaires) :
dans le cas d'un courant d'essai I0 par rapport à un courant I, (partie gauche du schéma ci-dessous), la force est radiale (cf. supra #formule-Ampere) ;
N.d.A. Je crois comprendre de la vidéo (i) qu'Haelterman appelle "champ de forces" un champ parallèle aux forces (sinon il s'agit d'un simple champ), et (ii) que ce qu'on entend par "matérialité du champ" (thèse de Faraday et Maxwell) est précisément que champ et force sont parallèles.
dans le cas d'une charge d'essai qm par rapport à un courant I (partie droite du schéma ci-dessous), la force est transverse (cf. supra #formule-Biot-Savart) ;
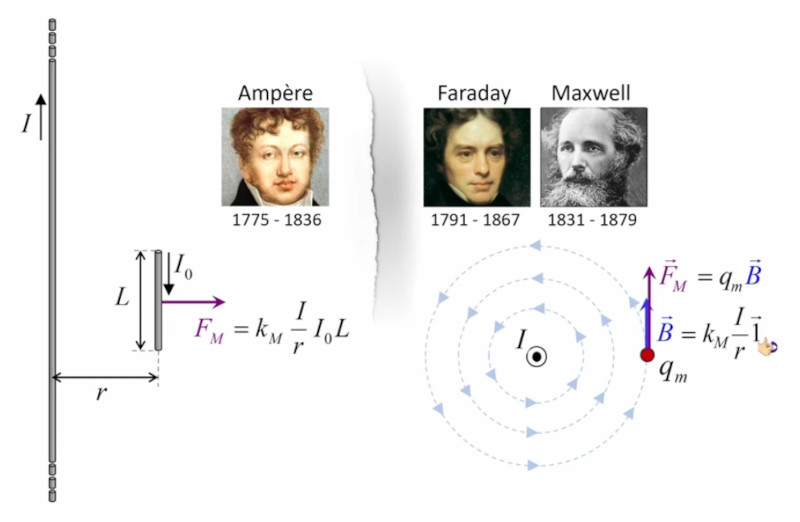
Dans la section suivante nous verrons pourquoi celle de ces deux options incompatibles qui est la bonne est celle fondée sur les charges magnétiques ... malgré qu'aucune charge magnétique n'a à ce jour été encore identifiée.
Pourquoi un champ de force pour le monopôle magnétique
Dans la section précédente, nous avons exposé la notion de champ postulée par Faraday et Maxwell, qui associent une matérialité physique au concept mathématique de champ vectoriel, faisant de celui-ci un champ de forces. Nous pouvons maintenant expliquer pourquoi ces scientifiques du 19° siècle ont choisi pour le champ magnétique (B→) un champ de forces qui agit sur des monopôles magnétiques (qM), et non pas sur des courants électriques.
Comme illustré dans la partie droite du schéma infra, Faraday et Maxwell se basent sur la loi de Coulomb de la force électrique F→ = kC * q * q0 / r 2 * 1r→
(205), étendu au cas de charges cette fois magnétiques :
F→M = kM * qM * qm / r 2 * 1r→
Faraday et Maxwell apportent une notion supplémentaire en attribuant la cause des forces F→M à l'action d'un champ physique (et non plus seulement vectoriel/mathématique), de sorte que l'on parle de champ de forces B→ = kM * qM / r 2 * 1r→ (283) tel que F→M = qm * B→ (282).
N.d.A. On comprend intuitivement que la nature radiale de ce champ (cf. le facteur 1r→, vecteur unitaire) est liée à la nature ponctuelle des objets physiques qu'il concerne, à savoir les charges magnétiques qM et qm.
Nous verrons que Maxwell et le mathématicien Laplace vont ainsi pouvoir non seulement formaliser l'interaction magnétique entre courants au moyen de la formule de Bio et Savart B→ = kM * I / r * 1→⊥ (284), mais en outre pouvoir modéliser de façon standardisée des configurations quelconques, et pas seulement de courants parallèles.
Il y a là une "étrangeté conceptuelle", consistant en deux faits contre-intuitifs : (i) on a toujours pas identifié à ce jour de charges magnétiques (qu'Ampère considérait même comme n'existant pas), et (ii) la formule de Bio et Savart associe la force magnétique à un champ transverse (cf. le facteur 1→⊥), de sorte que le champ magnétique associé aux interaction entre courants (qui sont radiales) n'est donc pas un champ de force.
Démonstration
par l'absurde
Pour comprendre ce qui a conduit Faraday et Maxwell à ne pas poursuivre la voie théorique d'Ampère – un champ de magnétique lié à des courants – nous allons tenter d'emprunter cette voie, afin d'en constater les conséquences bloquantes, lorsque l'on veut développer un modèle théorique permettant d'expliquer l'interaction magnétique entre courants d'orientations relatives quelconques.
Ce présent exercice, illustré dans la partie gauche du schéma ci-dessous, revient à postuler que F→M = kM * 1/r * I0 * L * 1→r où l'élément de courant d'essai I0*L (cf. partie gauche du schéma ci-dessous) joue le rôle de la charge magnétique d'essai qm (partie droite du schéma), de sorte que B→ = kM * I / r * 1→⊥ (284) devient donc B→ = kM * I / r * 1→r (cf. l'indice r du vecteur unité) ⇔ F→M = I0 * L * B→ .

N.B. Pour un rayon r déterminé le système de gauche correspond à un cylindre, tandis que celui de droite correspond à une sphère. Leurs projections sur le plan horizontal sont identiques (cf. schéma suivant).
Dans le schéma suivant, le système de gauche du schéma précédent est vu à la verticale, afin de montrer la similitude avec la partie droite. La bulle qui complète la partie gauche représente la voie choisie par Farraday et Maxwell. On notera que les lignes de champs sont radiales dans le premier cas et circulaires dans le second, ce qui correspond à des orientations de champ perpendiculaires.
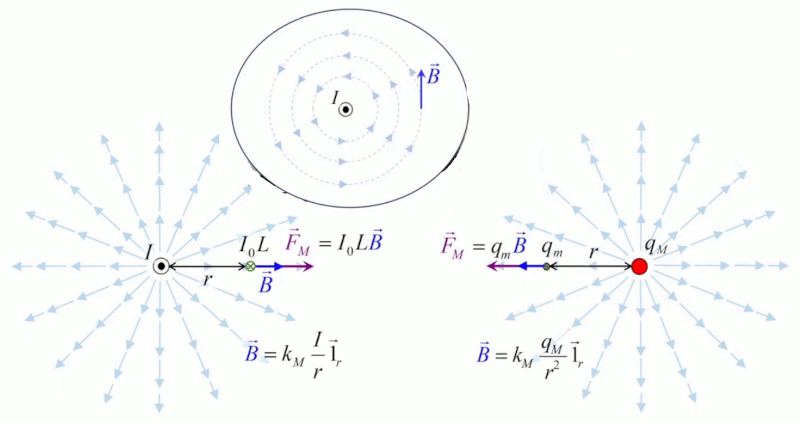
Une façon de montrer que la voie de gauche n'est pas pertinente consiste à exploiter les expériences d'Ampère lui-même, qui a vérifié toutes les configurations possibles, et pas seulement celles de courant parallèles. Or lorsque l'on tente d'élaborer un modèle de configurations quelconques (ce qu'ont réalisé Maxwell et Laplace), la voie de gauche conduit à une grande complexité voire à une impossibilité de calcul.
Prenons par exemple le cas de deux courants perpendiculaires. Dans la partie droite du schéma ci-dessous, lorsque l'on passe d'un courant d'essai vertical à horizontal, on observe que la force qu'il subit s'annule. Ce changement – que l'on observe pas dans le cas d'une charge magnétique d'essai – est du au fait que, contrairement à une charge (qui mathématiquement est ponctuelle), un courant a une direction/orientation déterminée dans l'espace, formulée par le vecteur I0 * L→.
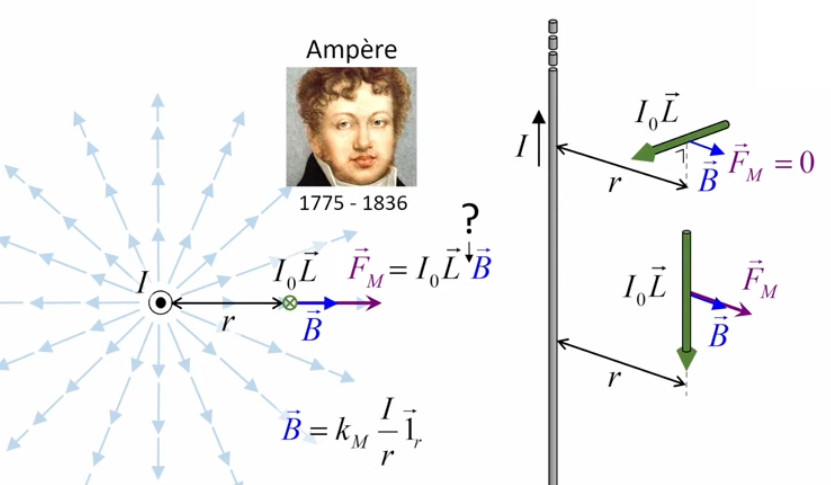
Le modèle mathématique de gauche permet-il d'exprimer la variation géométrique représentée dans le schéma de droite ?
Or il apparaît que dans ce cas, la nature de l'opération mathématique entre les vecteurs L→ et B→ de F→M = I0 * L→ * B→ est problématique (cf. point d'interrogation dans schéma de gauche ci-dessus). En effet, la partie droite du schéma ci-dessus montre que la configuration géométrique (c-à-d les positions relatives) correspondant à ce système de deux vecteurs I0*L→ et B→ est inchangée suite à sa rotation. Mais alors comment la force résultante pourrait-elle changer de non nulle à nulle ... ?
Ce qui explique la variation de la force, c'est évidemment la variation des orientations relatives des deux vecteurs "courant" I0 * L→0 (à droite dans les parties gauche et droite du schéma ci-dessous) et I * L→ (à gauche dans les parties gauche et droite du schéma), qui sont en interaction.
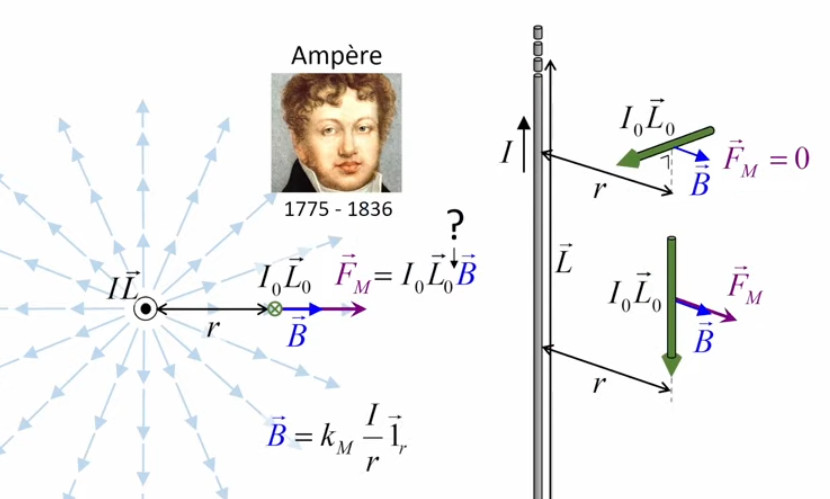
N.B. : les notations de longueur des vecteurs courant ont été adaptées, par rapport au schéma précédent.
Il faudrait donc compléter F→M = I0 * L→0 * B→ pour exprimer ces variations de positions relatives. Or cela serait extrêmement complexe. Pour s'en rendre compte, nous allons décrire,de façon très simplifiée, les travaux d'Ampère sur l'interaction entre deux éléments de courant de petites tailles. C'est l'équivalent, pour les forces magnétiques, de la situation imaginées par Coulomb pour formuler sa loi de force électrique FC = kC * q1 * q2 / r 2 (202).
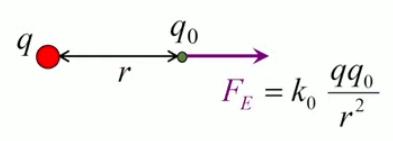
Cette dernière ne comprend que trois paramètres : q, q0, r. Par contre, la géométrie du modèle de l'électromagnétisme (cf. graphique suivant) est nettement plus complexe, car elle dépend de huit paramètres (dont des vecteurs) :
- intensités I et I0 et longueurs L et L0 des deux éléments de courant ;
- la distance r qui sépare les deux éléments de courant ;
- les angles α et β entre les deux vecteurs courant et l'axe qui les relie ;
- l'angle γ entre les plans déterminés par les deux couples vecteurs/axe.
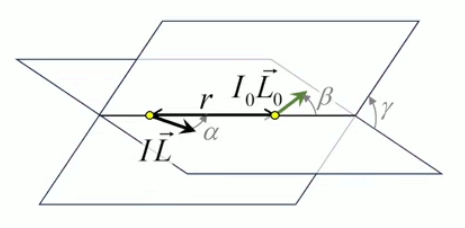
Ampère a certes pu formuler une équation correspondant à cette configuration :
FM = kM * I * L * I0 * L0 / r2 * (sinα * sinβ * cosγ - 1/2 * cosα - cosβ )
La dépendance est en r2 en raison de la petite taille des vecteurs courant.
Mais cette loi ne fonctionne que pour expliquer la loi de forces parallèles entre courant. C'est uniquement dans ce cas que l'on peut la ramener à F→M = kM * 1/r * I0 * L0 * 1→r.
Conclusion
Autrement dit, on ne peut trouver l'équation d'un champ magnétique qui soit un champ de forces pour les courants. On arrive donc à une situation apparemment paradoxale (illustrée par le schéma suivant) où, pour traiter les interactions entre courants, Maxwell et Faraday sont amenés à utiliser la notion d'un champ de force pour des ... monopôles magnétique plutôt que pour des courants électriques. Et comme dans le premier cas le champ est perpendiculaire à la force, le champs magnétique n'est donc pas un champ de forces pour le courant.

N.B. On est revenu à la notation originelle de la longueur du courant d'essai.
Le graphique montre que l'on peut utiliser la règle de la main droite pour déterminer l'orientation de cette force.
Le schéma ci-dessus représente le cas simple de courants parallèles. Mais nous allons voir que, partant du choix de l'approche de Maxwell & Faraday, et grâce aux travaux du mathématicien Laplace, nous allons pouvoir traiter les cas d'orientations quelconques. Avec la force magnétique de Laplace, on accède à la forme moderne de l'électromagnétisme.
La force magnétique de Laplace
La présente section est une introduction à la prochaine. Le schéma infra expose la base théorique duale sur laquelle Faraday a développé son modèle. Le schéma compare deux objets d'essai dans l'environnement d'un élément de courant :
à droite (modèle de Bio et Savart) : l'objet d'essai est une charge magnétique, la force qu'elle subit est proportionnelle notamment à la quantité de charge magnétique (notion de "monopôle magnétique") et sa direction est donnée par la règle de la main droite ;
à gauche (modèle d'Ampère) : l'objet d'essai est un élément de courant (ici parallèle), la force magnétique qu'elle subit est instantanée et à distance.
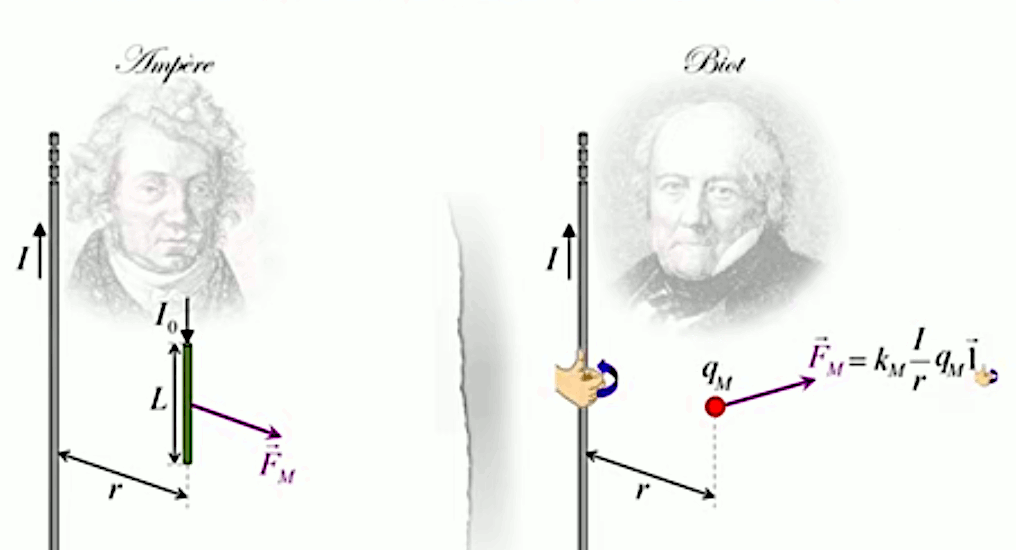
Faraday développe alors le modèle de Biot (partie droite du schéma suivant) en proposant que la force est causée par un champ magnétique enveloppant le monopôle magnétique. Ce champ magnétique étant de même direction que la force, il est dit "champ de force".

Mais il y a un "hic" : on a jamais observé de monopôle magnétique. Faraday se tourne alors logiquement vers les travaux d'Ampère (partie gauche du schéma suivant), en proposant que l'interaction entre les courants est causée par ce champ magnétique ⇔ il n'y a donc pas d'interaction instantanée et à distance entre les deux courants. Mais d'autre part, comme il apparaît que le champ magnétique n'a plus la direction de la force, il n'est plus un champ de force.
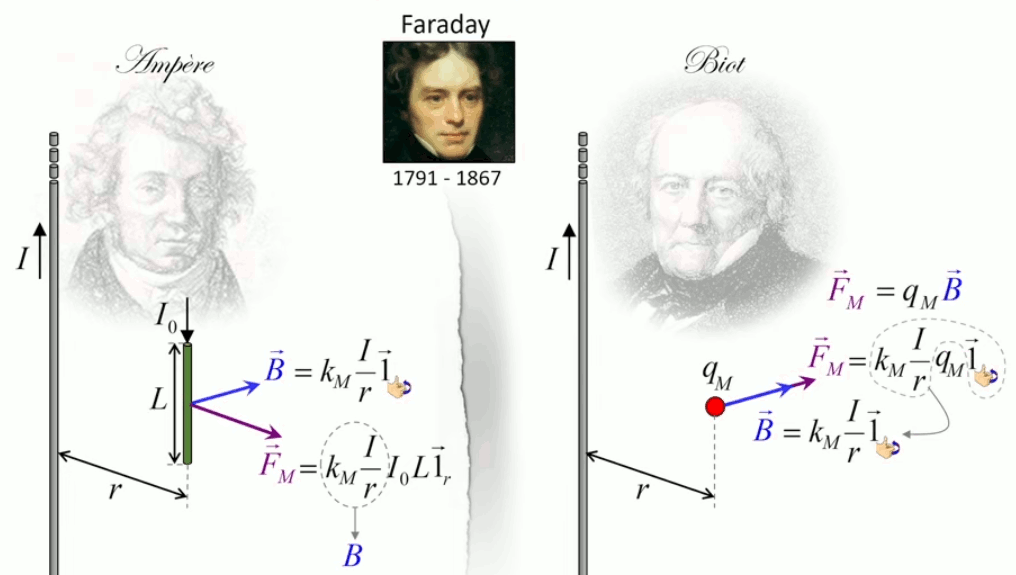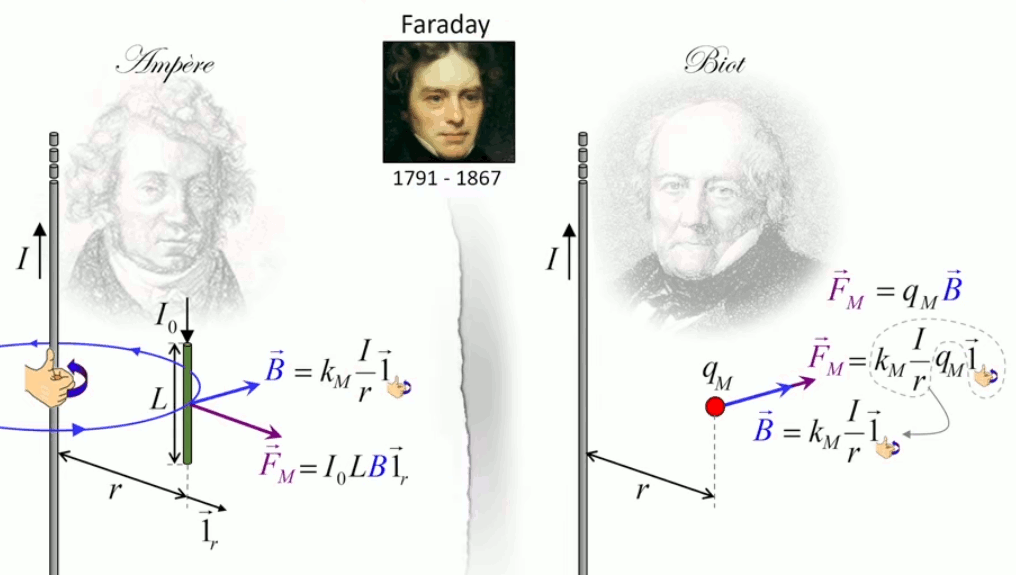
Soulignons que cette interprétation du modèle d'Ampère correspond au cas simple de deux courants parallèles (de sens opposés pour avoir une force répulsive), ce qui correspond à un champ magnétique de valeur identique tout le long de l'élément de courant I0*L (cf. schéma ci-dessous), par rapport auquel il est en outre perpendiculaire.
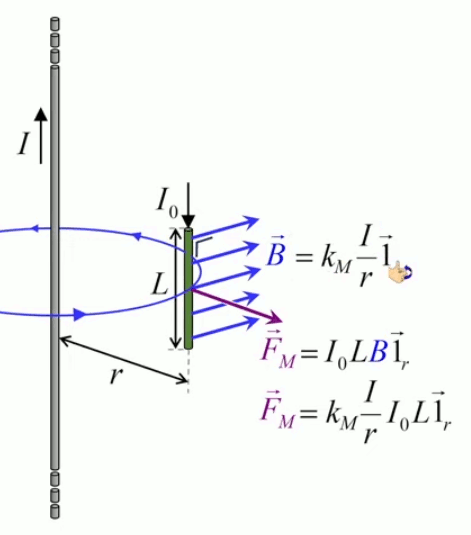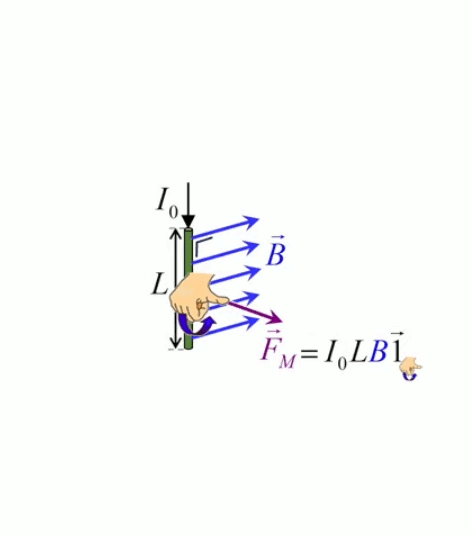
Abstraction est faite de l'objet d'environnement, et la direction de la force est alors déterminée par la règle de la main droite.
L'animation ci-dessus fait disparaître le courant d'environnement, illustrant ainsi que l'origine du champ magnétique n'est plus spécifiée. On passe donc de la thèse d'Ampère d'une interaction instantanée à distance entre deux courants, à l'action d'un champ magnétique enveloppant le courant, et qui n'est donc plus seulement un simple concept mathématique, mais revêt maintenant une véritable consistante physique.
On obtient ainsi la formule simplifiée de Laplace, où la force est calculée par rapport au module (et non pas au vecteur) du champ, sa direction étant déterminée par la règle de la main droite (cf. dans l'animation supra la modification de l'indice du vecteur unité : r est remplacé par l'icône "règle de la main droite" que nous noterons "md"):
F→M = I0 * L * B * 1→md
Comparons cette formule de la force magnétique de Laplace avec celle de la force électrique :
F→ = q0 * E→
(206)
où l'on peut réécrire le champ sous sa forme modulaire :
F→ = q0 * E * 1→E
Apparaît alors clairement l'analogie entre les objets d'essai des deux modèles : la charge q0 et l'élément de courant I0 * L, mais avec une différence fondamentale (cf. schéma ci-dessous) : dans ce second cas, la direction du champ n'est pas celle de la force qu'il suscite ... (NB : ce que rappelle les indices différents des vecteurs unités).
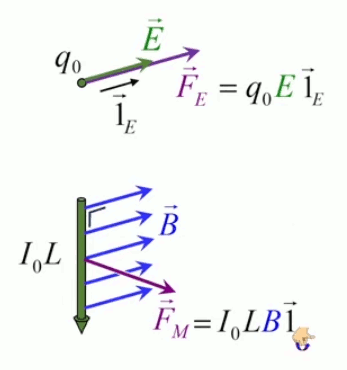
Selon l'analogie faite par Laplace, l'élément de courant I0 * L est à la charge q0 ce que le champ magnétique B est au champ électrique E (PS : dans la prochaine vidéo, nous verrons que l'élément de courant I0*L doit en réalité être considéré avec son caractère vectoriel, ce qu'illustre l'orientation de la flèche verte verticale, indiquant le sens du courant).
Pour illustrer la formule simplifiée de Laplace F→M = B * I0 * L * 1→md (289), une expérience consiste en deux aimants de mêmes orientations (cf. schéma suivant). On peut montrer que dans l'espace qui les sépare règne un champ magnétique relativement uniforme (région appelée "entrefer"). Si l'on introduit dans l'entrefer une tige conductrice d'un courant électrique, celle-ci subit alors une force. Sa direction est déterminée par la règle de la main droite (NB : la tige est perpendiculaire au champ magnétique). Le calcul de la valeur de F est alors facile : B et I sont est connus par hypothèse, et L est la longueur de la tige soumise au champs magnétique, c-à-d la largeur des aimants.
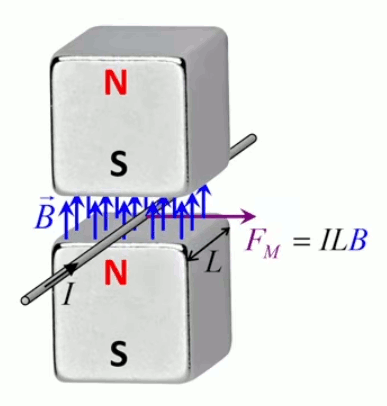
Une tige traversée par un courant est plongée perpendiculairement dans le champ magnétique d'un entrefer, et subit une force dont la direction est déterminée par la règle de la main droite.
Soulignons ici la simplicité de cette formule, surtout si on la compare avec celle d'Ampère, qui en raison de sa négation du champ magnétique, doit expliquer l'interaction entre les aimants et la tige conductrice par la thèse des courants de surface, dont non avons vu que la modélisation mathématique est hautement complexe :
FM = kM * I * L * I0 * L0 / r2 * (sinα * sinβ * cosγ - 1/2 * cosα - cosβ )
(288). En effet, le L et L0 de cette formule sont des longueurs de petits courants situés sur la tige (autant de Lo) et sur toutes les faces des aimants (autant de L), dont il faut calculer les interaction en mesurant les angles qu'ils forment ... La complexité calculatoire est donc gigantesque.
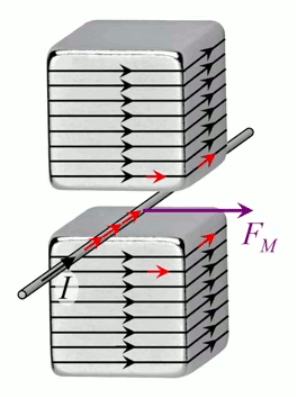
La formule de Laplace permet de calculer bien plus simplement la valeur du champ magnétique, par l'analogie avec la méthode utilisée pour le champ électrique, où une charge connue est placée dans le champ ⇒ il suffit alors de mesurer la force qu'elle subit suite à l'action du champ électrique, pour calculer la valeur de ce dernier. On va donc appliquer le même principe pour calculer le champ magnétique, et c'est l'élément de courant I*L qui joue le rôle de la charge électrique :
FM = I * L * B ⇒ B = FM / ( I * L ) qui définit la notion de champ magnétique, dans le cas particulier d'un champ magnétique perpendiculaire à la force qu'il exerce.
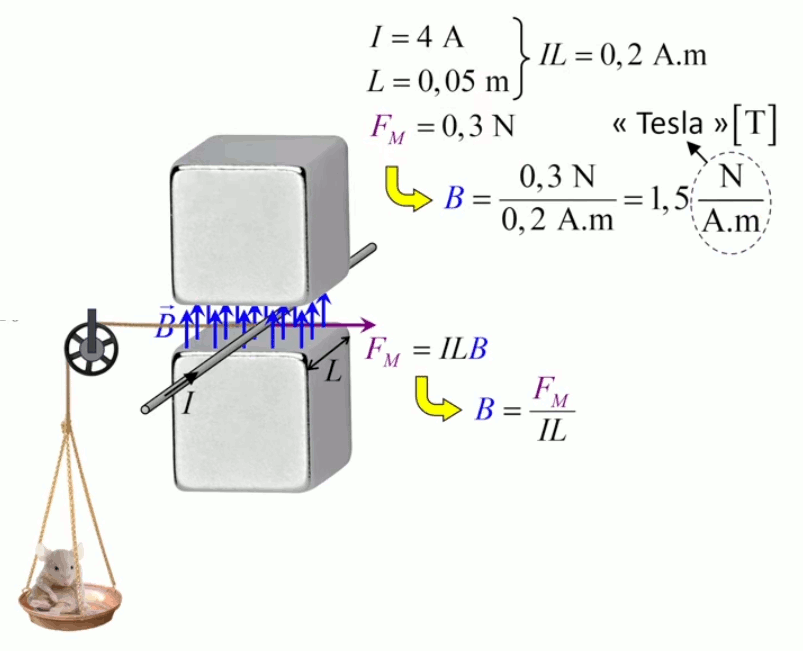
Alors que le calcul du champ électrique est simple puisqu'il est facile de mesurer une charge électrique, la situation est plus complexe pour le champ magnétique puisqu'on a toujours pas réussi à identifier une charge magnétique. On comprend alors l'aspect génial de la démarche de Faraday, qui nous permet malgré tout de calculer la valeur du champ magnétique, par association logique de l'élément de courant à la charge électrique !
Unité de
mesure
L'unité de mesure du champ magnétique est le tesla (T), c-à-d un newton par ampère*mètre (alors que l'unité du champ électrique c'est le newton par coulomb puisque l'objet d'essai est une charge électrique plutôt qu'un élément de courant).
Nikola Tesla, né le 10 juillet 1856 à Smiljan dans l'empire d'Autriche (actuelle Croatie) et mort le 7 janvier 1943 à New York, est un inventeur et ingénieur américain d'origine serbe. Il est connu pour son rôle prépondérant dans le développement et l'adoption du courant alternatif pour le transport et la distribution de l'électricité [source].
Ainsi le champ magnétique d'une valeur de 1 tesla génère une force de 1 newton sur un courant de 1 ampère de 1 mètre de long : FM = 1 A * 1 m * 1 N / ( A * m ) = 1 N. Ainsi le champ magnétique terrestre vaut 0,00005 T soit 0,05 mT (PS : cette faible force implique qu'une boussole doit minimiser suffisamment les forces de frottement pour fonctionner correctement).
Faisons maintenant le calcul pour un système composé de deux éléments de courant de 1 ampère et séparé par deux centimètres. On peut calculer la valeur du champ magnétique à partir de la formule de Bio et Savart B→ = kM * I / r * 1→⊥ (284) et de la valeur connue de la constante de force magnetique kM = 2 10-7 N / A2 (286). Le schéma suivant montre notamment que l'unité du champ B est bien le tesla.
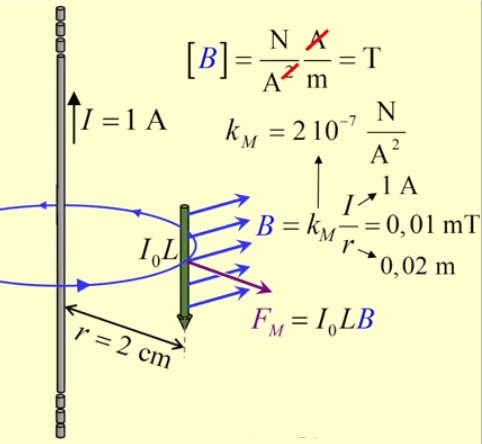
Ainsi le champ magnétique du système ci-dessus est de seulement un cent millième du champ magnétique généré par un aimant au neodyne. Cela signifie que les courants de surface par lesquels Ampère explique le magnétisme des aimants sont cent mille fois plus grands : puisque 1 ampère correspond 0,01 mT, alors 1 tesla correspond à 100.000 ampère ! Cela donne une idée de l'énorme ordre de grandeur des courants qui circulent à la surface des aimants. On comprend la difficulté qu'a du éprouver Ampère pour convaincre la communauté scientifique de l'ampleur de ces courants. Qui pourrait suspecter qu'un aimant de la taille d'une pièce de monnaie porte des dizaines voire des centaines de milliers d'Ampères ...?

La vidéo ci-dessous montre une expérience illustrant la force de Laplace. Le petit tube mobile est traversé par le courant, et subit donc la force générée par l'entrefer.
Rappelons que cette séance d'introduction se limite au cas simple d'un champ magnétique perpendiculaire à l'élément de courant, ce qui nous a permis d'étudier la formule simplifiée de Laplace c-à-d faisant abstraction de la nature vectorielle de l'élément de courant. Dans la vidéo suivante, cette nature vectorielle sera prise en compte pour faire tourner l'élément de courant.
Dans la vidéo précédente, on a introduit la formule simplifiée de la force magnétique de Laplace F→M = B * I0 * L * 1→md (289), qui correspond au cas de deux courants parallèles, et où la force est perpendiculaire au champ magnétique qui la provoque, et à l'élément de courant sur laquelle elle s'exerce (ce qu'indique l'indice "règle de la main droite" du vecteur unitaire).
Pour généraliser au cas de courants d'orientations quelconques (c-à-d pas nécessairement perpendiculaires au champ magnétique), il nous faut introduire la notion de vectorialité du champ B→ ainsi que de l'élément de courant I*L→ (qui dans la formule simplifiée sont considérés en tant que simple modules).
Pour ce faire, le système expérimental illustré ci-dessous est composé d'une tige conductrice en forme de U carré, plongée dans le champ d'un entrefer (le schéma fait ici abstraction de l'aimant supérieur, dans une vue du haut). Si la tige en U carré est orientée perpendiculairement au champ magnétique de l'entrefer, elle subit alors une force F→M = B * I0 * L * 1→md (289). La règle de la main droite permet de déterminer le sens de trois forces subies par la tige. L'animation ci-dessous montre que les forces exercées sur les deux segments parallèles s'annulent, de sorte que seule subsiste la force qui tire l'ensemble de la tige hors de l'entrefer.
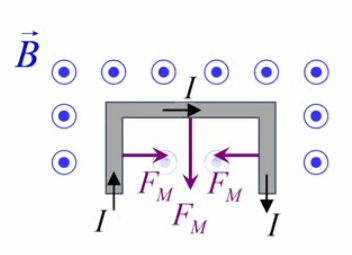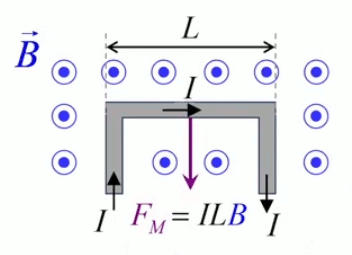
Les symboles "pointe de flèche" indiquent que le champ B→ sort du plan de ton écran, dans cette représentation vue du haut.
Nous allons maintenant étudier l'effet d'une inclinaison du plan de la tige, sur la force qu'elle subit. L'animation suivante montre que cette rotation a pour effet de réduire l'intensité de la force (NB : mais sans modifier sa direction !).

L'inclinaison de la tige en U provoque la réduction du module de la flèche mauve.
Suite à l'inclinaison illustrée ci-dessus, l'angle (noté θ) que forme l'élément de courant par rapport au champ magnétique n'est plus nécessairement un angle droit. C'est donc la grandeur de cet angle qui détermine celle de la force. Pour mesurer cette relation F(θ), le point de vue de l'animation suivante est à nouveau de face (partie gauche), et la variation de la force FM en fonction de l'angle θ est notée dans un repère orthonormé (partie droite). La partie gauche de l'animation représente les deux points extrêmes du graphe de la fonction FM(θ), pour une rotation de 0 à 90° :
la direction du courant (de la base du U) est parallèle au champ (θ=0°) ⇒ la force est nulle;
la direction du courant (de la base du U) est perpendiculaire au champ (θ=90°, situation correspondant à la formule simple de Laplace) ⇒ la force est maximale et vaut I*L*B.
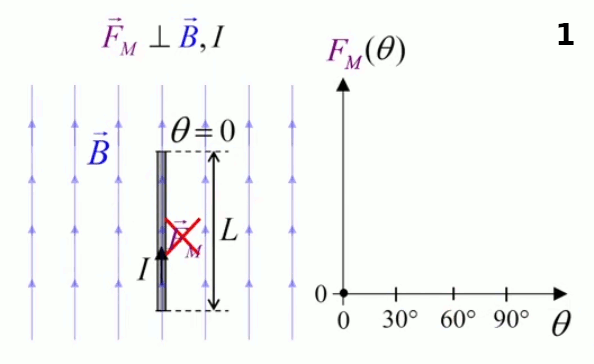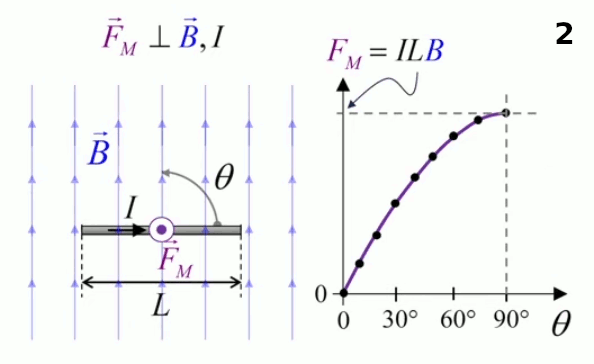
L'observation des valeurs intermédiaires (30°, 45%, 60°, ...) révèle que la direction de la force magnétique F→M est inchangée (elle reste perpendiculaire au champ B→ et à l'élément de courant I), mais que son module dépend de l'angle θ, selon la fonction sinus(θ) :
FM = I * L * B * sinθ (NB : sin(0)=0 et sin(90)=1).
En effet, nous avons vu que sin(θ) ≡ côtéOpposé / hypothénuse (31) où l’hypoténuse est ici l'élément de courant de longueur L, et le côtéOpposé à θ est la projection de cet élément de courant sur la direction perpendiculaire au champ magnétique (cf. schéma ci-dessous). D'un point de vue physique, on peut voir la projection L*sin(θ) comme la longueur de l'exposition de l'élément de courant L à l'effet du champ magnétique : ainsi quand l'élément de courant est parallèle au champ magnétique, son exposition est nulle, ce qui correspond bien à sin(0)=0, et à l'opposé, son exposition est maximale en cas de perpendicularité, ce qui correspond à sin(90)=1.
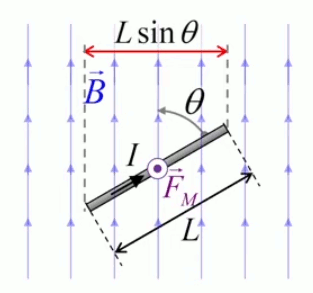
Le graphique suivant illustre un élément fondamental de la règle de la main droite : le sens de repliement des doigts correspond toujours au sens le plus cours entre les deux segments de l'angle. Autrement dit, l'angle entre deux vecteurs ne dépasse jamais 180° ! Donc la valeur "physique" d'un angle de 270°, puisqu'il est supérieur à 180°, est de 270-360=-90°. Ainsi, la partie gauche du schéma ci-dessous montre que l'angle mesuré à 270° correspond en réalité à 360-270=90° mais correspond à un courant (et, partant, une force) de sens opposé (cf. les différences de sens entre parties supérieure et inférieure de la partie gauche du schéma ci-dessous).
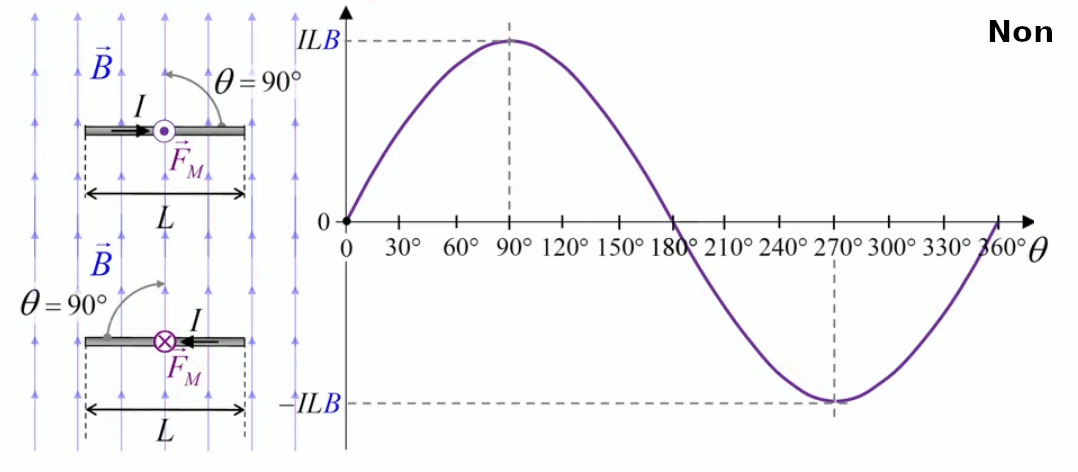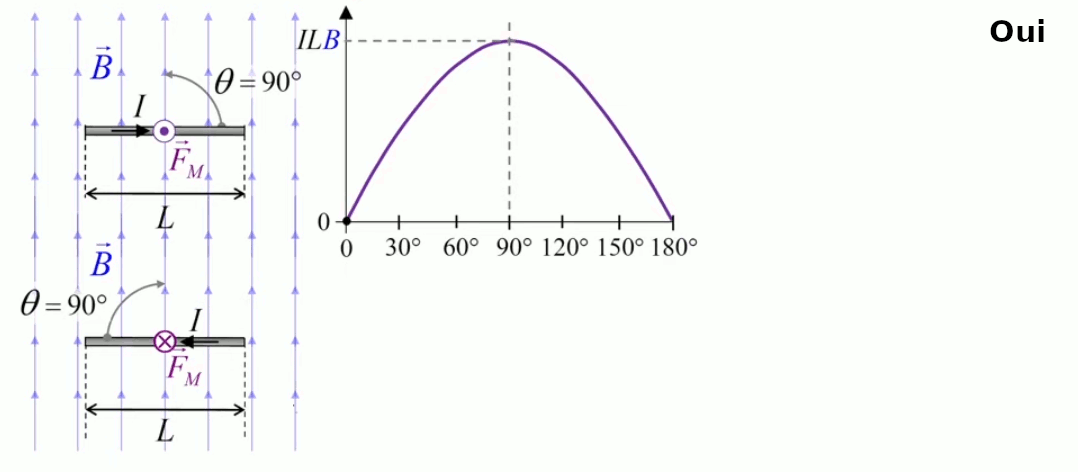
Partie droite : une force de module négatif, ça ne fait pas sens. Partie gauche : des courants opposés subissent des forces magnétiques opposées (cf. supra #courant-champ-magnetique).
Les deux lignes suivantes résument la forme généralisée de la formule de Laplace. La seconde ligne exprime que pour tout angle θ entre le champ B→ et l'élément de courant I, on peut appliquer la règle de la main droite pour déterminer le sens de la force F→, car cette force est perpendiculaire à B→ et I (qui déterminent l'angle θ).
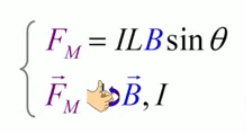
Une formulation plus rigoureuse des ces deux lignes est la notion de produit vectoriel inventée par Hermann Grassmann et développée par Williard Gibbs (PS : on parle de force de Laplace uniquement dans le monde francophone, mais de force de Grassmann dans le reste du monde ...).
Le schéma suivant montre que :
la force F→M est perpendiculaire au champ B→ et à l'élément de courant I*L→ ;
l'angle θ entre le champ B→ et l'élément de courant I*L→ est quelconque
le module de la force F est le produit entre module du champ B, module de l'élément de courant I*L, et sinus de l'angle entre champ et élément de courant ;
par conséquent, le vecteur force F→ peut être exprimé comme produit vectoriel entre l'élément de courant I*L→ et le champ magnétique B→ ;
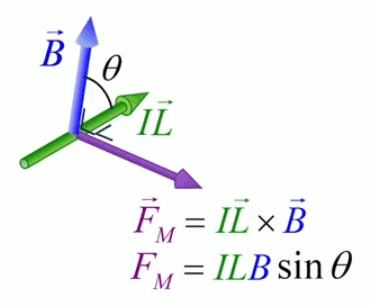
Ainsi la force de Laplace s'exprime comme le produit scalaire de l'élément de courant et du champ, et son module est obtenu par l'ajout du facteur angulaire sin(θ) :
- vecteur : F→M = I * L→ x B→
- module : FM = I * L * B * sin(θ)
Les trois vecteurs F→, L→ et B→ peuvent être représentés dans un espace cartésien, ce qui permet d'exprimer leur valeur en fonction de leur composantes spatiales (par exemple Lx, Ly et Lz pour l'élément de courant L).
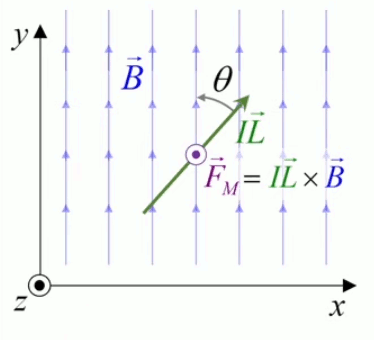
Ainsi notamment l'élément de courant peut alors être exprimé comme la somme des projections de ses composantes en x, y et z : L→= Lx * 1→x + Ly * 1→y + Lz * 1→z, ou encore plus simplement comme triplet de nombres : L→= Lx, Ly, Lz (cf. supra /geometrie#vecteur).
On va ainsi pouvoir calculer les composantes Fx, Fy et Fz à partir du pseudo-déterminant du produit vectoriel I * L→ x B→ (cf. supra /geometrie#produit-vectoriel-calcul).
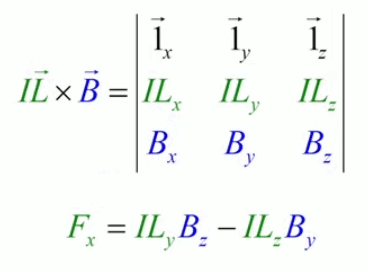
Le pseudo-déterminant permet de calculer également Fy et Fz.
De la force de Laplace à la force de Lorentz
Nous allons ici analyser l'origine physique de la forcé magnétique de Laplace, ce qui va nous conduire au concept de force électromagnétique ou encore force de Lorentz, force fondamentale de la nature.
L'analogie entre magnétisme et électricité faite par Laplace (cf. supra) a ses limites. En effet, alors que l'expression de la force électrique F→ = q0 * E→ (206) peut être appliquée au niveau fondamental d'une particule élémentaire (q0) – électron (charge négative) ou proton (charge positive) –, la formulation de la force magnétique de Laplace F→M = I * L→ x B→ (290) ne peut être appliquée à une échelle microscopique, puisque la notion de courant I, sur laquelle elle repose, correspond à un grand nombre de particules élémentaires (qu'Ampère appelait "molécules d'électricité"). Ainsi un courant est qualifié de phénomène collectif, c-à-d dire non réductible (en tant que tel) à un de ses éléments.
L'électron n'a été découvert que quatre-vingts ans après Ampère, par Joseph Thomson.
Reprenons le montage expérimental de la section précédente : un tige de courant immergée dans l'entrefer d'un aimant en U. Dans le schéma ci-dessous, le système est vu du haut (comme si l'observateur voyait à travers la partie supérieure de l'aimant en forme de U) : le champ "sort de l'écran" (cf. les symboles "pointe de flèche"), et le courant se dirige vers la droite (cf. vecteur unitaire). L'élément de courant I*L→ correspond à la longueur L de l'entrefer. La direction de la force est alors identifiée par la règle de la main droite.
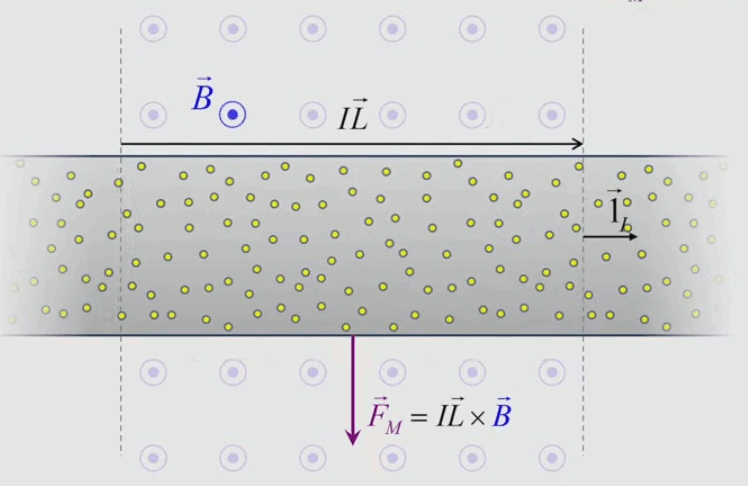
N.B. Comme déjà fait pour la loi d'Ohm, on suppose que les électrons sont de signe ... positif (raison pour laquelle ils sont représentés en jaune alors que la couleur conventionnelle pour les charges négatives est le noir), ce qui permet de poser que le courant se déplace dans le même sens que ces charges électriques. Cela permet de simplifier le raisonnement : on n'est plus obligé de préciser à chaque fois que la force va dans le sens opposé au champ.
Pour introduire ces particules élémentaires dans notre formulation, nous allons apporter quelques transformations à la force de Laplace F→M = I * L→ x B→ (290).
La première consiste à exprimer le vecteur L→ comme étant le produit de son module par le vecteur unitaire dans sa direction c-à-d dans le sens du courant :
F→M = I * L * 1→I x B→
Passons maintenant au courant électrique I. Il s'agit d'un débit de charge Q correspondant au nombre de charges q passant par la section d'entrée pendant une période de temps Δt :
I = Q / Δt [C/s = A]
Calculons maintenant la valeur Δt déterminée par le déplacement d'un électron à la vitesse v sur la longueur L de l'entrefer (distance entre sections d'entrée et sortie de l'élément de courant I * L→) : dès lors que
v = L / Δt ⇒ Δt = L / v
que l'on substitue dans l'expression de I précédente ⇒
I = Q * v / L ⇒
que l'on substitue supra dans l'expression de F→ précédente ⇒
F→ = Q * v * 1→I x B→ ⇒
en vectorisant le module v par son produit avec le vecteur unitaire 1→I ⇒
F→M = Q * v→ x B→
Les deux expressions de la force de Laplace. La comparaison ci-dessous des deux formes de la force magnétique est assez intuitive : dans la première formulation, un courant I sur une longueur L correspond, dans la seconde formulation, à une charge Q (collective, car correspondant à l'élément de courant) se déplaçant à une vitesse v :
La seconde formulation de la force magnétique est à priori surprenante : nous savions qu'un champ magnétique provoque une force sur un courant électrique (première formulation ci-dessus), mais il ressort de la seconde formulation que ce serait sur des charges électriques – composant (transportées par) le courant – que cette force serait exercée ! Mais alors quelle est la différence entre champ magnétique et champ électrique ?
La réponse saute au yeux : la différence entre
F→ = q0 * E→ (206)
et
F→M = Q * v→ x B→ (292)
c'est le facteur vitesse v→ : le champ magnétique agit sur des charges électriques par l'intermédiaire de leur vitesse.
Pour éclairer cette conclusion, une parenthèse est nécessaire : un fil conducteur de courant placé dans un champ électrique ne subit pas de force électrique ! La raison en est qu'un milieu conducteur est neutre électriquement (sa charge est nulle). En effet, par "conducteur" on entend le fait que les atomes qui constituent le fil ont libéré chacun un électron (signe négatif), de sorte que les atomes sont ainsi devenu positifs ("ions positifs"). Or comme leurs nombres sont identiques, le signe de la charge Q, composée par l'ensemble de ces charges de signes opposés, est donc nul. Par conséquent, il résulte de F→ = Q * E→ (206) que cet ensemble subit une force électrique nulle.
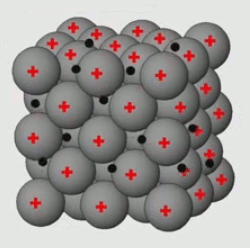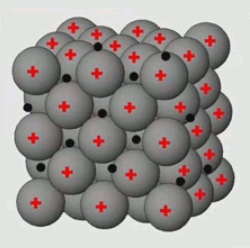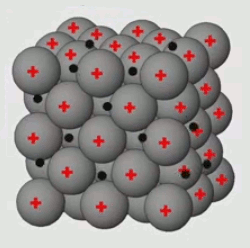
Les ions positifs (marqués par un signe + rouge) sont fixes, tandis que les électrons (en noir) sont libres (l'animation illustre leur agitation thermique).
Ainsi alors que le champ électrique agit de façon symétrique sur les électrons (signe négatif) et les ions positifs, ce n'est pas le cas du champ magnétique. Celui-ci n'agit manifestement pas de la même façon sur les charges positives que sur les charges négatives : puisqu'il exerce bien une force sur l'élément de courant, c'est nécessairement que les forces exercées sur ces charges de signes opposés ne s'annulent pas.
Mais pourquoi la force magnétique agit-elle sur les seuls électrons et pas sur les ions positifs ? La réponse réside dans F→M = Q * v→ x B→ (292) : les propriétés physiques (en l'occurrence cinétiques) des électrons sont différentes : alors que les électrons sont en mouvement (à une vitesse v>0 ⇒ F→M>0), les ions positifs sont fixes (v=0 ⇒ F→M=0).
Fermons la parenthèse, et revenons à nos moutons. Pour passer à l'échelle microscopique, il suffit alors d'exprimer le fait que la charge Q est composée de N charges élémentaires : Q = N * q ⇒
F→M = Q * v→ x B→ (292)
devient
F→M = N * q * v→ x B→
Questionnement. Cette dernière formulation soulève cependant une question fondamentale : peut-on considérer que chacun des électrons subit une même force magnétique f→M = q * v→ x B→, toutes étant dirigées dans la même direction ? (cf.illustration ci-dessous).
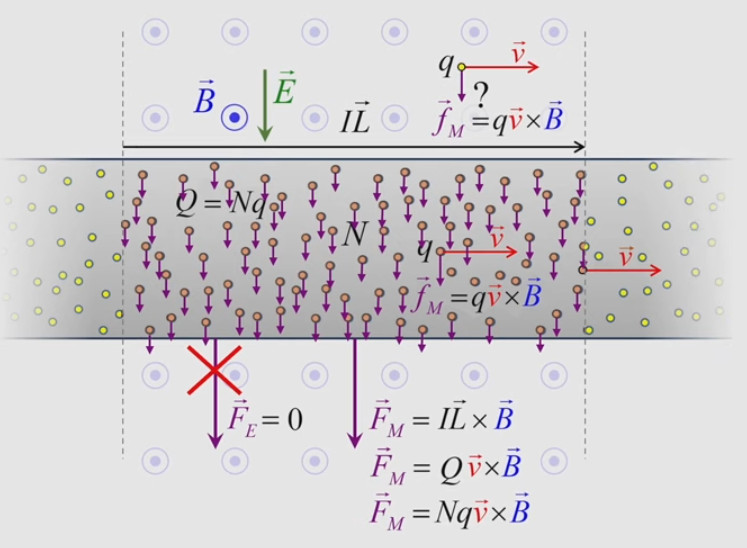
Autrement posé : dans F→M = N * q * v→ x B→ (293) peut-on poser N=1 ? Faut-il répondre par la négative, puisqu'une force magnétique est supposée agir sur un courant électrique, "phénomène collectif" par nature ?
D'autre part, dans le raisonnement que nous avons développé jusqu'ici, le vecteur v→ représente la vitesse moyenne du nuage (gaz) d'électrons libres composant la charge Q. Or en réalité la vitesse de chaque électron est d'orientation quelconque, car ces électrons sont déviés par (i) les ions immobiles, (ii) les parois constituées par les forces de cohésion, (iii) l'agitation thermique. Par conséquent, les forces subies par ces électrons ont également des orientations quelconques ⇒ il ne semble pas pertinent de supposer qu'elles vont se combiner systématiquement dans la même direction que F→M = N * q * v→ x B→ (293).
La voie rigoureuse pour répondre à la question posée consiste en un développement mathématique de physique statistique, trop complexe pour le public de clipedia. Une voie alternative consiste en une expérience de la pensée. Supposons ainsi une tige de plexiglas – donc neutre électriquement – que l'on frotte sur toute sa longueur avec un tissus, afin de la charger en électrons de façon uniforme. Substituons-là à la tige de notre système expérimental. La différence est que cette fois les électrons ne sont pas en mouvement puisque la tige, bien qu'électrisée, n'est pas conductrice de ces électrons. Par conséquent, puisque les électrons sont fixes relativement à l'élément de courant, la problématique supra est résolue. D'autre part, on peut mettre les électrons en mouvement relativement à l'entrefer en déplaçant la tige elle-même, de sorte que l'on obtient ainsi des conditions expérimentales équivalentes au cas d'une tige conductrice ! Par conséquent, si la tige électrisée subit la même force magnétique, on peut alors en déduire que le passage de F→M = Q * v→ x B→ (292) à F→M = N * q * v→ x B→ (293) n'est pas abusif.
Avant de poursuivons notre expérience de pensée, soulignons cependant une différence avec notre système expérimental originel : la tige en plexiglas n'étant pas neutre, puisqu'elle n'est pas conductrice, elle subit donc un champ électrique associé aux charges électriques négatives qui lui ont été transmises par frottement. Cependant, dans le cadre de notre expérience de pensée, nous pouvons l'ignorer.
Poursuivons notre expérience de pensée, en considérant cette fois une tige de plexiglas dont seulement une partie a été électrisée. La conséquence est qu'il n'y a plus d'élément de courant, c-à-d de courant sur toute la longueur L de l'entrefer.
L'éxpérimentation montrant que la force magnétique exercée sur la tige subsiste malgré l'absence d'un élément de courant, on en conclut que des deux formulations
c'est la seconde qui décrit généralement les déterminants physiques de la force magnétique, la première équation décrivant seulement le cas particulier de charges sur toute la longueur de l'entrefer.
Ainsi l'expérimentation montre que lorsque l'on déplace la tige, celle-ci ne subit la force magnétique que pendant le passage du nuage de charge Q dans l'entrefer.
L'étape finale de notre expérience de la pensée consiste en un nouvelle réduction d'échelle, cette fois en considérant un seul électron au lieu d'un nuage d'électrons. Et l'on constate qu'il n'y a aucune raison que cela change quoi que ce soit à la logique du phénomène étudié.
On obtient alors la formule de la force magnétique de Lorentz, qui concerne le niveau microscopique (donc fondamental, alors que la formule de Laplace se limite au niveau macroscopique) :
f→M = q * v→ x B→
On peut donc faire abstraction de la tige et considérer le cas d'un électron lancé dans l'espace d'un entrefer, à une vitesse horizontale. On comprend intuitivement que l'électron va alors être dévié vers le bas (ce que confirme l'expérimentation).
L'approche de Lorentz est générale car il prend en compte la présence du champ électrique évoqué plus haut, raison pour laquelle on parle de force électromagnétique de Lorentz :
f→EM = q * E→ + q * v→ x B→
qui concerne la force subie par une charge électrique en présence d'un champ magnétique et d'un champ électrique.

Nous allons considérer ici la force de Lorentz en l'absence de champ électrique. Autrement dit, nous allons nous intéresser à la seule composante magnétique de la force de Lorentz (que l'on peut également appeler "force magnétique de Lorentz").
Mais avant, il est utile de refaire un bilan historique. On est passé, sur une période de six siècles, par trois étapes conceptuelles majeures :de Pierre de Maricourt à Biot et Savart (13° → 19° siècle) : le monopole magnétique, est agent du champ magnétique et objet de la force magnétique ;
Ampère (19° siècle) : interaction magnétique entre courants électriques ⇒ l'élément de courant se substitue au monopôle magnétique dans la théorie du magnétisme, pendant 80 ans, jusqu'à :
Lorentz : en toute généralité : (i) une charge électrique subit une force qui comprend deux composantes : électrique et magnétique ; (ii) la charge électrique en mouvement est l'agent du champ magnétique et objet de la force magnétique.
Soulignons que la notion d'élément de courant n'est pas pour autant obsolète. Elle aujourd'hui toujours est utilisée pour décrire le phénomène magnétique au niveau macroscopique, et donc sur les applications technologiques du magnétisme (cf. moteur électrique), tandis que la notion d'électron en mouvement décrit le magnétisme, plus fondamentalement, au niveau microscopique (physique fondamentale du magnétisme).
Venons-en à la force magnétique de Lorentz f→M = q * v→ x B→ (294). Ce produit vectoriel traduit un effet géométrique, du au fait que l'élément de courant est un élément vectoriel, d'orientation quelconque par rapport au champ magnétique. L'expérimentation montre que l'angle de cette orientation détermine, via le sinus de cet angle, le module de la force magnétique : FM = I * L * B * sin(θ)(291) ⇒ on applique cette formulation géométrique à (294) ⇒
fM = q * v * B * sin(θ)
Le schéma suivant illustre le fait qu'une charge qui se déplace traverse des lignes de champ magnétique avec une certaine inclinaison, d'angle θ. On peut alors réécrire (296) en fonction de la projection sin(θ) du module vitesse v, c-à-d parallèlement au vecteur champ, de sorte que cette projection orthogonale (notée v⊥) est perpendiculaire au vecteur champ (cf fonction sinus : (31) ). Autrement dit, v⊥ = v * sin(θ) est la composante de la vitesse, perpendiculaire au champ magnétique.

Notez le symbole "pointe de flèche", montrant que la direction du vecteur force est déterminée par la règle de la main droite.
Le module de la force magnétique de Lorentz peut alors être formulé par fM = q * v⊥ * B
Interprétation. On dit que le produit vectoriel f→M = q * v→ x B→ (294). effectue la "sélection" de la composante de la vitesse, perpendiculaire au champ.
C'est donc l'opposé du produit scalaire, qui projette le premier vecteur du produit perpendiculairement au deuxième vecteur (⇒ projection parallèle), tandis que le produit vectoriel projette le premier vecteur parallèlement au second (⇒ projection perpendiculaire).
On peut voir v⊥ comme la vitesse avec laquelle la charge traverse les lignes de champ. Si elle ne les traverse pas, cela signifie qu'elle se déplace parallèlement aux lignes de champ : θ=0 ⇒ sin(θ)=0 ⇒ fM = q * v * B * sin(θ) = 0 (296). Autrement dit, si l'on veut supprimer l'interaction de la charge avec le champ, malgré sa vitesse, il faut orienter la vitesse dans la direction du champ.
Même effet si θ=180° (→ sin(θ)=0) de sorte que l'on se déplace alors vers le bas dans le schéma supra.
Il résulte de fM = q * v⊥ * B (297) que la force magnétique ne dépend donc que de la composante perpendiculaire. Ainsi l'illustration suivante montre que des vitesses plus grandes ou plus petites, mais avec une même composante perpendiculaire, provoqueront la même force magnétique (en module comme en direction) exercée sur la charge ! Il ressort de fM = q * v * B * sin(θ) (296) qu'une vitesse v plus grande (/petite) est compensée par un angle θ plus petit (/grand). C'est en cela que le produit vectoriel effectue une sélection de la composante perpendiculaire de la vitesse. Autrement dit : la composante longitudinale n'intervient pas dans la force magnétique.

D'autre part, on notera que la force la plus petite pour une force donnée est telle que θ=π/2 ⇒ sin(θ)=1 ⇒ par (296) : fM = q * v * B . Autrement dit, le mode d'interaction le plus efficace entre la charge électrique et le champ magnétique s'obtient en traversant les lignes de champ perpendiculairement : max(sinθ) ⇒ max(fM) :

La formule simplifiée de la force magnétique de Laplace FM = I * L * B * sin(θ) (291) nous permet de calculer la valeur du champ magnétique. Il suffit de prendre un élément de courant de valeur connue et de la placer perpendiculairement au champ :
FM = I * L * B ⇔
B = FM / ( I * L ) [N/(A*m)=T]
Rappel : le tesla (T) est l'unité du champ magnétique. Il représente le champ qui exerce une force de 1 N sur un élément de 1 ampère et d'un mètre de long.
Revenons à la force de Lorentz fM = q * v⊥ * B (297). Nous voyons quelle fournit une nouvelle manière de définir le champ magnétique, ou de mesurer le champ magnétique en un point de l'espace. Il suffit de mettre en mouvement une charge électrique perpendiculairement au champ ⇒
B = fM / ( q * v ) [N/(C*m/s)=N/(A*m)=T]
Nous obtenons alors une nouvelle interprétation du Tesla : c'est le champ magnétique qui exerce une force de 1N sur 1C se déplaçant à une vitesse de 1m/s, perpendiculairement au champ.
Expérimentation. Pour vérifier expérimentalement la validité de f→M = q * v→ x B→ (294), on prend un pendule constitué d'une boule en plastique, que l'on frotte avec une étoffe afin de l'électriser par frottements ⇒ on obtient la charge q. On plonge alors la boule dans le champ magnétique d'un aimant orienté de telle façon que le pôle nord soit orienté vers la boule. Si la boule est immobile, sa vitesse est nulle, et elle ne subit donc pas de force magnétique. Lui imprimer un mouvement vertical n'est pas une solution puisque dans ce cas il n'y a pas de composante vitesse perpendiculaire au champ.

On va donc placer la boule de telle sorte que l'angle θ est optimal, soit θ=π/2.

La théorie nous dit que si la boule est déplacée le long du trait hachuré, la boule sera poussée dans la direction de f→M lorsque la boule passera au-dessus de l'aimant. Cependant, en pratique, cette expérience est très difficile à réaliser, en raison de la charge gigantesque que représente 1 coulomb. Pour s'en rendre compte, tentons de rassembler deux demi-sphères qui contiennent chacune 1/2 coulomb. Pour ce faire, il faut vaincre les forces de répulsion de la loi de Coulomb F(r) = kC * q1 * q2 / r 2 (202) dont nous avons vu que la constante est gigantesque : kC = 8,99 * 109 N * m2 / C2 (203). Ainsi, pour les rapprocher à une distance de seulement 1 mètre il faudra exercer une force de près de deux milliards de newtons, ce qu'aucune machine actuelle ne pourrait réaliser !
Une charge réaliste pour cette expérience ne devrait pas dépasser le milliardième de coulomb. Avec une boule suffisamment grande, sans doute pourrait-on arriver à accumuler une dizaine de nano-coulombs, mais avec un fort risque de claquages en raison des forces de répulsion entre les électrons ⇒ éclair ⇒ la charge disparaît. D'autre part, même si on y arrivait, on obtiendrait une force également plus faible d'un ordre du milliardième : 1 nano newton, est extrêmement faible, de sorte que le déplacement de la boule serait imperceptible.
Ce résultat expérimental est assez surprenant : avec la force de Laplace, on pouvait facilement observer une force magnétique de 1 N (cf. supra #force-magnetique-Laplace), alors que dans le cas de la force magnétique de Lorentz, on pourrait seulement observer un nano-newton.
Quelle en est donc la raison ? Elle se trouve dans l'égalité I * L→ = Q * v→ (cf. supra #Laplace-Lorentz). Ce ne peut être la vitesse v des électrons dans l'élément de courant du système expérimental de Laplace, qui est très faible, de l'ordre du mm/s, soit encore mille fois plus petit que le m/s de la formule de Lorentz. C'est donc dans la charge Q que se trouve l'explication. Dans :
I * L = Q * v
prenons une vitesse de 0,001 m/s ⇒
1 Am = Q * 0.001 Cm/s ⇔
Q = 1000 C
soit douze ordres de grandeur de plus que la charge que l'on tentait d'obtenir dans notre pendule !
Mais comment se fait-il que l'on puisse rassembler 1000 C dans un fil d'un mètre de long, alors que nous n'arrivons pas à utiliser une charge douze milliards de fois plus petite dans la boule du pendule ? La raison réside dans le fait que le fil de courant est un corps neutre, c-à-d que les électrons en question sont fournis par les atomes de ce même fil. Ce n'est qu'en rapprochant ces électrons à une échelle subatomique qu'ils vont interagir (répulsion). À l'échelle macroscopique, la densité des électrons par unite de volume est donc la même que la densité des atomes, donnée par le nombre d'Avogadro : NA ≡ N(1g) = 6,022140 76 * 1023 (191) électrons par cm3. Revenons à notre expérience de la pensée consistant à tenter d'approcher deux demi-sphères de 1/2 C : si elles sont neutres, alors elles ne subissent pas de forces de répulsion.
Les matériaux conducteurs sont ainsi virtuellement "magiques" : ils permettent une gigantesque concentration d'électrons, qui en outre peuvent être mis en mouvement en leur appliquant une différence de potentiel en leurs bornes. La faible vitesse de ce mouvement est compensée par l'ampleur de la charge. C'est ce principe qui est au coeur des applications technologiques du magnétisme, fondées sur la force de Laplace.
Revenons enfin à notre question originelle : comment démontrer expérimentalement la force de Lorentz ? C'est Joseph Thomson; le découvreur de l'électron, qui y répondra, comme nous le verrons dans la vidéo suivante.
Optique
2. Loi de Snell-Descartes
3. Captation d'image
4. Lentille convergente
5. Relation de conjugaison des lentilles
6. Lentille divergente
7. La vision
La lumière
Sans forme, sans masse, qu'est-ce donc que la lumière ? Au 19° siècle Maxwell, a développé un modèle mathématique ("équations de Maxwell" ou encore "équations de l'électrodynamique") décrivant la lumière comme une onde électromagnétique plane, c-à-d l'association d'un champ électrique sinusoïdal, exprimé en volts par mètre (V/m), et d'un champ magnétique ,de même période, exprimé en ampères par mètre (A/m). Les ondes électromagnétiques sont donc la manifestation d’une interaction à distance, mais « retardée » (c-à-d non instantanée).
Équations de Maxwell et champ électromagnétique
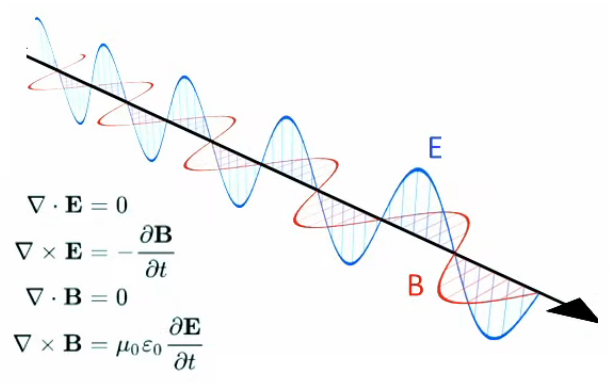
E : champ électrique ; B : champ magnétique. Nous avons étudié en détail la première de ces équations (232) : ici le membre de droite est nul car la masse est nulle ⇒ ρ=0.
N.d.A. Champ électrique vs magnétique. Un champ électrique existe par la seule présence d'une charge immobile (absence de courant, appareil électrique éteint), et lié à la tension (mesurée en V/m). Le champ est dit magnétique dans le cas de charges en mouvement (courant, appareil électrique allumé), et lié à l'intensité (mesurée en Ampères/m).
Nous allons traiter ici uniquement du champ électrique. Celui-ci est l’expression d’une interaction à distance entre charges électriques (la force électrique). Par définition chaque charge électrique génère un #champ-electrique.
Supposons donc une charge positive, par exemple un proton (noyau de l'atome d'hydrogène). Ainsi le champ électrique exprime l'influence à distance que le proton exerce dans son espace environnant, le champ électrique s'exprimant par une force sur toute autre charge située dans le champ. Remplaçons le proton par un atome d'hydrogène c-à-d ajoutons-lui son nuage d'électron. Celui-ci étant de charge négative son champ est orienté vers le noyau, et comme la charge du noyau vaut celle du nuage en valeur absolue, toute charge dans l'environnement de l'atome subit donc une force nulle. Cela est du moins le cas en situation dite d'équilibre ou de repos ...
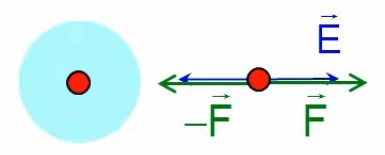
Deux champs sont exercés sur la charge de droite :
• le champ du proton, extraverti;
• le champ du nuage électronique, extraverti.
Mais si l'on déstabilise l'atome, par exemple en le chauffant, de sorte que son environnement s'agite ⇒ l'atome subit des chocs ⇒ il se met à vibrer. ⇒ cette vibration est répercutée sur le champ électrique ⇒ sur les charges qui y sont situées. Ainsi un atome dans un état asymétrique (c-à-d déformé en raison d’une perturbation extérieure) peut générer une force électrique (un champ électrique) sur une charge située dans son environnement (N.d.A. : la situation moyenne de l'atome oscillant est celle de l'atome au repos).
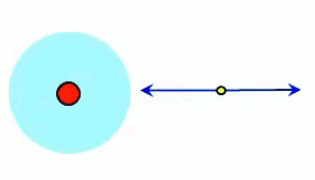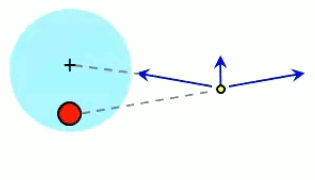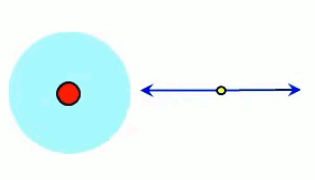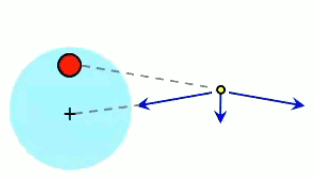
Avec l'oscillation de l'atome vibrant, les deux champs ne se compensent plus ⇒ l'oscillation de l'atome se répercute dans le champ dipolaire.
Ce que Maxwell a découvert est que cette interaction dynamique n'est pas instantanée : la vibration met un certain temps à se propager (cf. le δt dans les équations de Maxwell supra) : plus la charge est éloignée du proton, plus il faut de temps pour que la vibration l'atteigne. Maxwell montre en outre que la vitesse de propagation de cette vibration, c-à-d de cette onde, est celle de la lumière, soit environ 300.000 km/s.

Le sommet de la vague se propage à la vitesse de la lumière. NB : dans cette animation il est fait abstraction de la diminution du module du champ avec la distance.
Cette non-instantanéité de l'interaction électrique est donc directement liée à la formation des ondes électromagnétiques : celle-ci sont ainsi vues comme la simple manifestation d’une interaction à distance, variable et retardée.
Sens de
la vue
Le sens de la vue (la perception de la lumière) résulte de l’interaction électrique à distance entre des atomes de notre environnement et les molécules photosensibles de la rétine. Lorsque l'onde atteint la rétine qui se trouve au fond de l'oeil, elle transmet la vibration aux charges électriques constituant les atomes des cellules de la rétine.
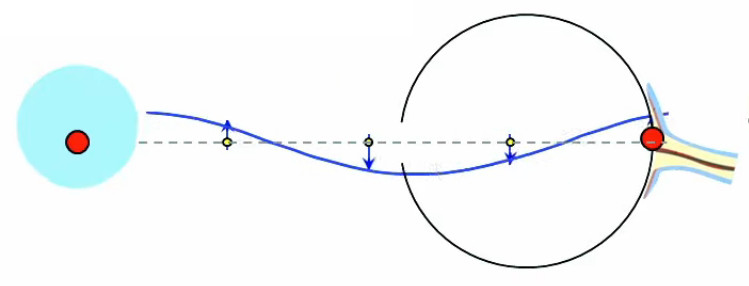
N.d.A. La relation entre l'oeil et l'objet regardé, est très semblable à la relation entre antennes réceptrice et émettrice.
Ces cellules opèrent alors une réaction électrochimique générant un signal sur le nerf oculaire. Ce signal est alors conduit à la région du cerveau traitant les signaux visuels, sur base desquels le cerveau va former une image, en l'occurrence un point lumineux (N.B. Le graphique ci-dessous montre que le cerveau doit intervenir pour rétablir le bon sens de l'image inversée qui est captée par la rétine recouvrant la paroi intérieure du globe oculaire. Ce phénomène de croisement des rayons lumineux au niveau de la pupille sera approfondi plus loin, lorsque nous étudierons les lentilles).
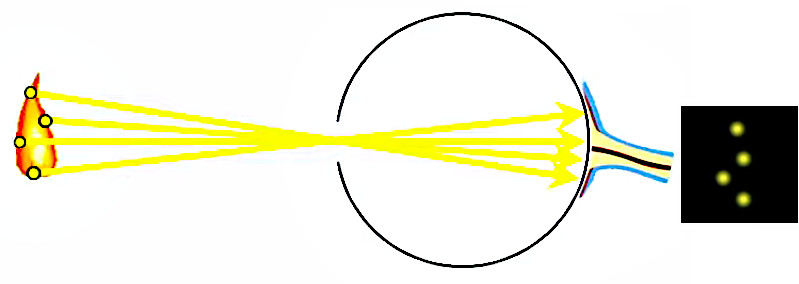
Un corps (ici une flamme) est composé de points, et il en est de même pour son image.
La notion d'onde électromagnétique doit être interprétée avec prudence : rien ne vient "frapper" la rétine ! Il ne s'agit pas d'une onde de déplacement (comme sur un corde), mais seulement de la distribution de la valeur du champ le long du rayon. La notion d'onde n'est que l'expression de la propagation, c-à-d de la non instantanéité, de l'interaction. Or si l'interaction était instantanée, il n'y a pas de raison pour qu'elle n'opère pas. Par conséquent la notion d'onde n'est pas nécessaire pour expliquer le phénomène lumineux ! La seule oscillation du champ électrique au niveau de la rétine suffit à elle seule à provoquer la vision. On ne s'étonnera donc pas de constater que la lumière est invisible ...
Nous avons vu que le champ électrique et le champ magnétique sont des concepts théoriques abstraits (cf. #champ-electrique) qui ne peuvent aucunement se voir dans la mesure où ils ne diffusent pas la lumière. La lumière est donc invisible, tout comme le champ magnétique qui attire une épingle sur un aimant. Pour bien comprendre cela il est utile de définir ce que signifie "être visible" ou encore "voir". Être visible signifie "réfléchir" la lumière. Or un corps ne peut réfléchir la lumière que s'il est composé de matière. Si la lumière est invisible c'est parce qu'elle n'est pas de la matière. Elle ne peut donc ni réfléchir d'autres rayons, ni "frapper" la rétine.
Ainsi les rayons lasers que l'on croit "voir" (par exemple dans les boîtes de nuit) ne sont que des particules en suspension dans l'air (gouttelettes d'eau, poussières, ...), qui réfléchissent la lumière propagée par la source lumineuse : les charges électriques qui composent les atomes de ces particules sont mises en oscillation par le rayon laser, de sorte qu'elle vont réfléchir le rayon laser ⇒ certains des rayons réfléchis vont aller dans la direction de l'oeil de l'observateur. C'est le même phénomène que l'on observe lorsque les rayons du soleil traversent des nuages ou pénètrent dans un sous-bois humide (mais la couleur observée est bien celle de la lumière qui éclaire). Ainsi si la lumière était visible nous ne verrions rien d’autre que la lumière elle-même car elle masquerait les objets qui nous entourent.
Loi de Snell-Descartes
Une lentille sphérique convergente a la forme d'une intersection de deux sphères (NB : l'image ci-contre ne donne qu'une vue en deux dimensions). L’axe qui passe par les centres des sphères est appelé "axe optique" de la lentille.
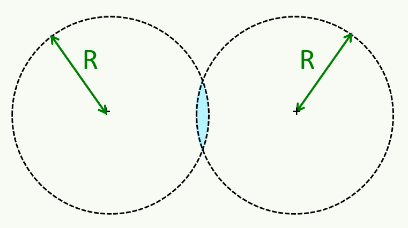
Une lentille sphérique est caractérisée par l'indice de réfraction (n spécifique au matériau constituant la lentille), par son épaisseur et par les rayons de courbure de ses faces (c.-à-d. les rayons de chacune des deux sphères). S’ils ont la même valeur (R) la lentille est dite "symétrique".
On caractérise la déviation d'un rayon passant au travers d'un dioptre (ici air-verre) relativement à la normale (c-à-d la perpendiculaire) au point d'entrée sur la lentille. Le matériau de la lentille est caractérisé par son indice de réfraction n (n(verre) = 1,5, n(vide) = 1) tel que l'angle réfracté θr est différent de l'angle incident θi. La loi de la réfraction, ou loi de Snell-Descartes nous dit que :
sin(θr) = sin(θi) / n
NB : dès lors que n > 1 ⇒ θr < θi
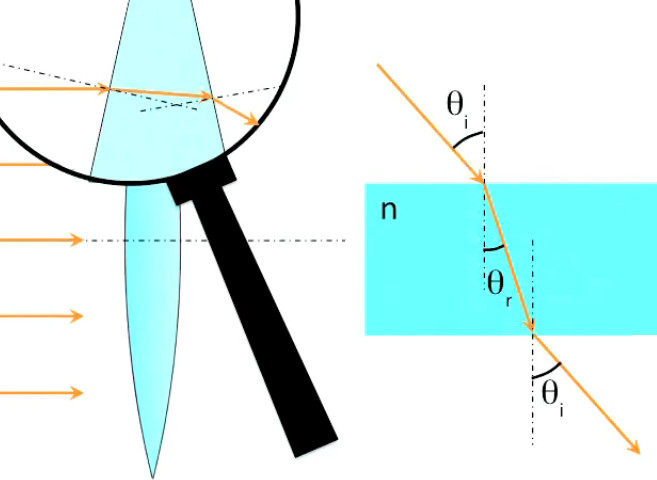
La partie droite de l'image ci-dessus montre que si les faces d'entrée et de sortie d'un dioptre sont parallèles, la réfraction (déviation) est nulle. La partie gauche de l'image montre que la courbure de la lentille a pour effet de réfracter (dévier) des rayons parallèles, en les concentrant. Ce n'est que pour le seul rayon confondu avec l'axe de la lentille que la réfraction est nulle. Plus on s'écarte de cet axe, plus l'inclinaison de la lentille est élevé par rapport à cet axe ⇒ plus la réfraction est élevée.
Focalisation
Une lentille sphérique (symétrique ou non) induit donc un effet de focalisation des rayons qui la traversent. Cette focalisation est telle que les rayons incidents parallèles à l'axe optique sont réfractés en convergeant vers un même point de l'axe optique, appelé "foyer" de la lentille. Et plus généralement, les rayons seulement parallèles entre eux se croisent dans le "plan focal" de la lentille, plan perpendiculaire à l'axe optique et passant par le foyer.
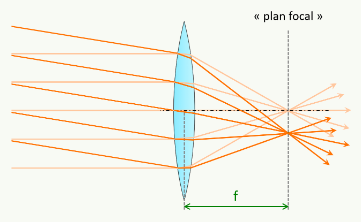
NB1 : cette illustration pourrait correspondre au cas de deux étoiles, dont l'une est dans la ligne de l'axe optique (rayon parallèles à l'axe optique), et l'autre se trouve à côté de la première (⇒ rayon non parallèles à l'axe optique). NB2 : cette illustration 2D ne montre pas la troisième dimension de la réfraction, à savoir que même les rayons (parallèles) sortant du plan de l'illustration se croisent en un même point du plan focal.
La distance f entre le foyer et l'axe la lentille est appelé "distance focale". Celle-ci dépend des caractéristiques de la lentille : la courbure des rayons (déterminée par R) et l'indice de réfraction (n) du matériau composant la lentille. On peut montrer que la relation entre ces trois grandeurs peut être approchée par :
f ≈ R / 2 * ( n - 1 )
NB : n(verre) ≈ 1,5 ⇒ R = f
Loi des
lentilles
minces
Cette approximation (299) n'est cependant valable que pour une lentille sphérique suffisamment mince, c’est-à-dire dont les centres des sphères qui la dessinent ne sont pas trop proches. Plus précisément, l'épaisseur et le diamètre de la lentille doivent être petits relativement aux deux rayons de courbure (c-à-d les rayons R1 et R2 des deux sphères qui la dessinent).
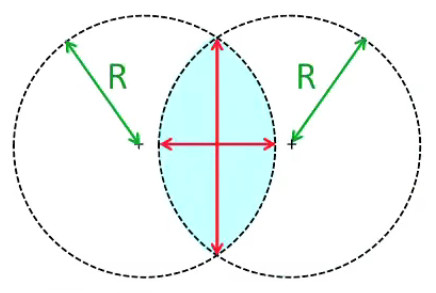
En effet, pour des lentilles trop larges relativement aux rayons de courbure, la concentration des rayons n'est plus ponctuelle, mais répartie sur une zone de réfraction (N.d.A : on comprend déjà ici intuitivement une possible cause d'image floutée). Plus un rayon lumineux est éloigné de l'axe optique, plus tôt il coupe celui-ci, par rapport aux rayons moins éloignés de l'axe optique, qui lui sont pourtant parallèles.
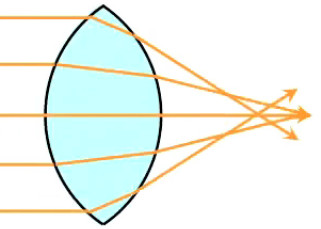
Nous étudions ici le cas des lentilles minces, dont les deux propriétés principales sont donc :
des rayons parallèles (entre eux, c-à-d pas nécessairement parallèles à l'axe optique) se croisent en un même point du plan focal
un rayon d'angle d'incidence quelconque passant par le centre de la lentille n'est pas dévié.

N.B. Il n'y a pas de déviation angulaire, mais il y a cependant une déviation de translation (N.d.A. : sauf pour le rayon confondu avec l'axe optique). Dans le cas d'une lentille mince cette déviation de translation est négligeable. Notons à cet égard que l'on modélise graphiquement une lentille mince par un simple double flèche (↕), de sorte que la double réfraction du biface est simplifiée en une réfraction unique.
Règle de
réfraction
Dans le cadre des lentilles minces, ont peut alors appliquer les deux propriétés énoncées supra, pour déduire le trajet de n'importe quel rayon réfracté par la lentille qu'il a traversée : il suffit de tracer sa parallèle passant par le centre de la lentille ⇒ son intersection avec le plan focal détermine le point focal, par lequel passe aussi le rayon dont on a pris la parallèle.
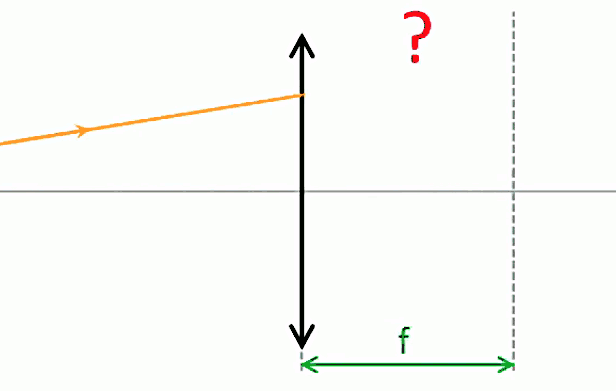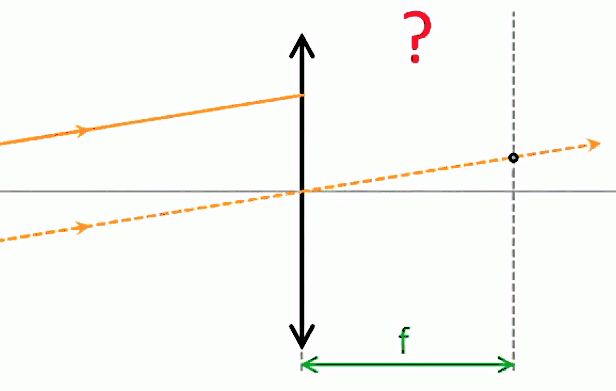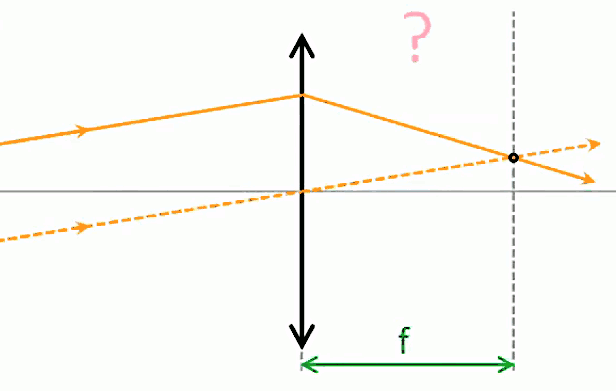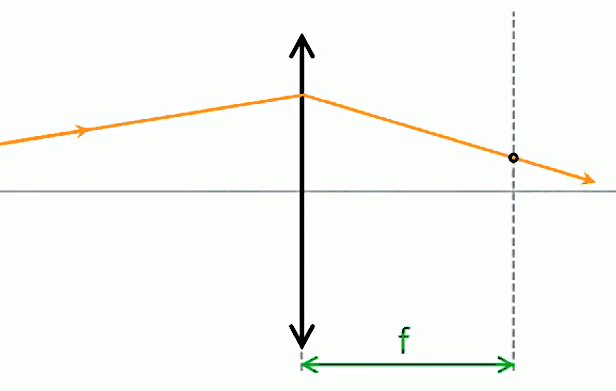
Réversibilité
de la réfraction
La symétrie du phénomène étudié ici implique que dans tous ces raisonnements on peut inverser le sens de propagation de la lumière. Pour s'en rendre compte il suffit d'étudier le cas particulier d'un rayon d'angle d'incidence quelconque, mais dont la réfraction est parallèle à l'axe optique. Le graphique ci-contre montre par construction géométrique que le point où ce rayon croise l'axe optique avant de passer par la lentille, doit être situé à une distance égale à la distance focale.
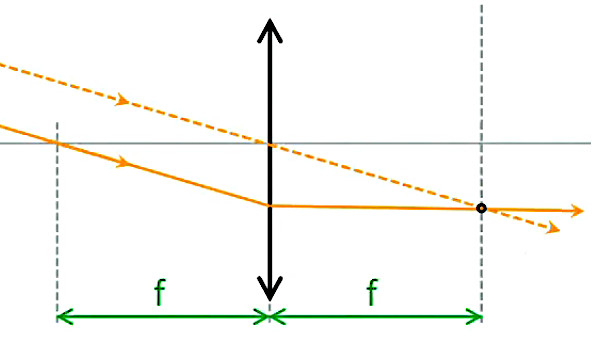
Captation d'image
Qu'est ce qui fait, d'un point de vue physique, que l'on voit un objet ? (l'explication biologique sera développée plus loin). Nous allons montrer que la lentille permet de former une image, pouvant alors être imprimée sur une surface photosensible (rétine de l'oeil ou film d'un appareil photo). Mais pour cela il faut d'abord comprendre ce qui se passe avant que la lentille capte les rayons lumineux réfléchis dans sa direction.
Alors que la surface d'un tuyau de cuivre apparaît à l'oeil nu comme parfaitement lisse, ce n'est plus du tout le cas lorsque l'observation est faite au moyen d'un microscope électronique (cf. photo ci-contre). En raison de ces multiples aspérités, c-à-d angles d'incidences, les rayons lumineux sont réfléchis dans toutes sortes de directions, phénomène appelé "diffusion".
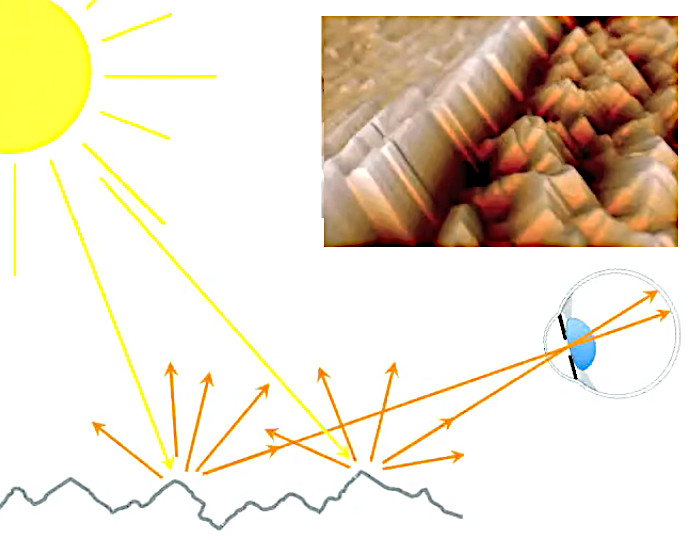
La lumière du soleil est ici représentée en jaune, mais en réalité la couleur des rayons solaires est blanche, ce qui signifie qu'elle comprend toutes les longueurs d'onde lumineuses (c-à-d toutes les couleurs de l'arc en ciel). Or, à l'instar des autres matériaux, le cuivre ne réfléchit pas de la même manière chacune de ces longueurs d'onde : en l'occurrence il réfléchit principalement les couleurs rouges orangées (les autres étant absorbées par le cuivre) : c'est ce qui fait sa couleur.
Mais comment peut-on voir la forme et les couleurs d'un objet ? On peut démontrer mathématiquement, qu'en raison des deux propriétés (*) des rayons réfractés par une lentille mince (celle constituée par l'ensemble "cornée+cristallin" de l'oeil, ou celle d'un appareil photo), tous les rayons diffusés par un même point, puis passant par cette lentille, convergent en un même point.
(*) Cf. supra : (i) des rayons parallèles se croisent en un même point du plan focal ; (ii) un rayon passant par le centre de la lentille n'est pas dévié.
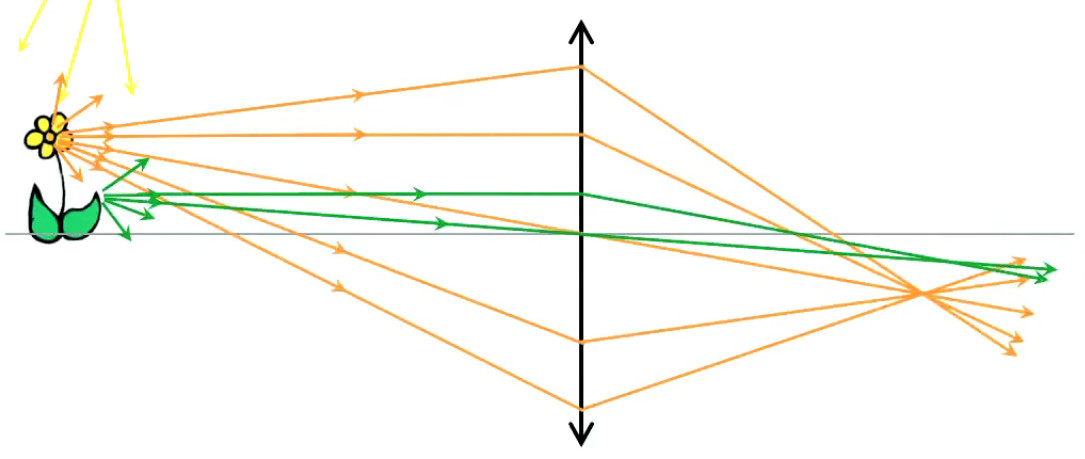
PS : nous verrons plus loin que si l'objet est éloigné de la lentille par une distance supérieure à la distance focale, la convergence a lieu vers la droite de la lentille, et inversement.
Il apparaît ainsi que la lentille a pour effet de reproduire une image de chacun des points de l'objet diffusant la lumière du soleil (N.d.A. : il s'agit donc d'une image en 3D). Par conséquent, si à l'endroit de cette image se trouve une surface photosensible, alors l'image pourra y être "imprimée" c-à-d "enregistrée".
On comprend alors la problématique, dite de "mise au point", résultant du fait que l'image de l'objet est en 3D, alors que la surface photosensible est en 2D. La mise au point consiste à placer cette surface au niveau des points de l'image (foyers image) que l'on souhaite y imprimer avec le plus de précision (les autres points ne seront pas nets, mais floutés). En pratique c'est la distance entre la surface photosensible et la lentille qui est ajustée.
Dans le cas de l'enregistrement d'images par l'oeil :
- rétine : surface photosensible ;
- cornée + cristallin : lentille ;
- cristallin : permet d'ajuster la distance focale via la courbure du cristallin.
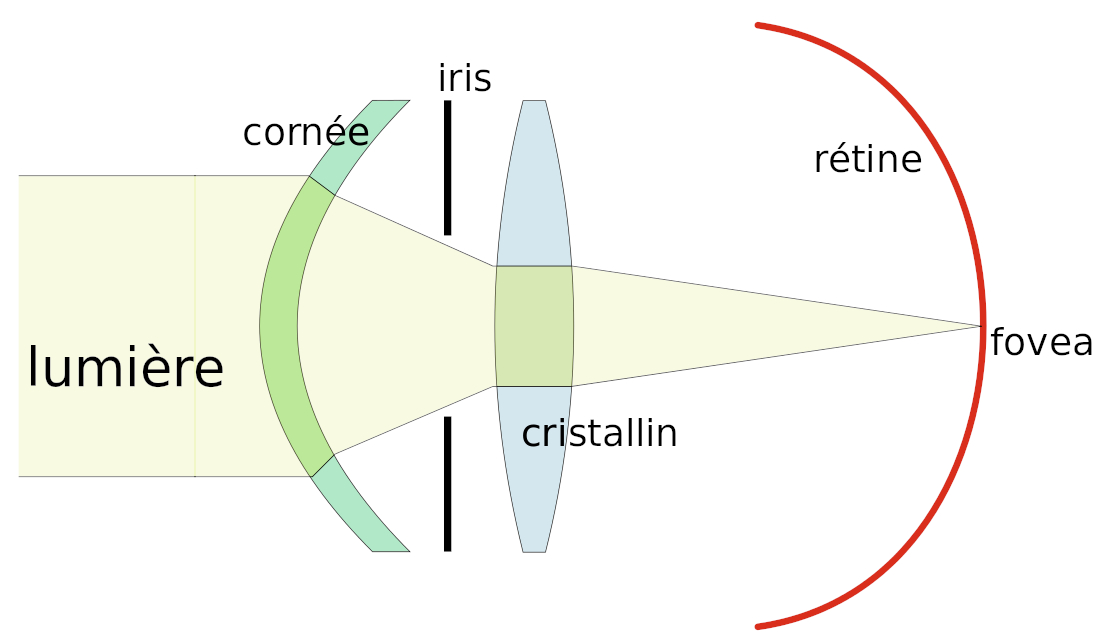
Dans le graphique ci-dessus, la pupille est le trou au milieu de l'iris. L'ensemble cornée+cristallin forme un système à deux lentilles, celle du cristallin étant adaptative grâce à sa compression par des muscles situés au-dessus et en-dessous.
Lentille convergente
Comme chaque point de l'objet diffuse de nombreux rayons lumineux, ceux qui arrivent dans la pupille de l'oeil sont divergents (sauf si le point objet est situé à l'infini, dans lequel cas les rayons qu'ils diffusent peuvent être considérés comme parallèles). Par conséquent, sans adaptation de l'oeil, ces rayons imprimeraient sur la rétine une tache lumineuse ⇔ ce point serait "flouté". Pour que les rayons soient concentrés sur un même point (foyer image) de la rétine, les muscles du cristallin se contractent pour le comprimer ⇒ accentuer son rayon de courbure ⇒ faire converger les rayons. Cependant la faculté d'ajustement du cristallin n'est évidemment pas infinie : au repos il est conçu pour induire une convergence optimale de rayons incidents parallèles, ce qui est approximativement le cas des points situés suffisamment loin de l'oeil. Il existe une distance appelée "punctum proximum" (notée p) en-deçà de laquelle un objet ne pourra pas être vu net, car le cristallin est à son maximum de contraction. Sa valeur est de 10 à 50 cm pour l'humain, selon l'âge, et avec lequel elle augmente (myopie).
Or pour voir un objet plus grand, l'oeil doit s'en rapprocher. Mais que faire s'il à déjà atteint la distance p ? Réponse : utiliser une lentille convergente, aussi appelée "loupe" !
Nous allons voir qu'une lentille convergente est telle que les rayons lumineux diffusés par un même point de l'objet, sont réfractés par la lentille de sorte que la convergence a lieu :
- vers la droite de la lentille (⇒ formation d'une image réelle, renversée) si l'objet est éloigné de la lentille par une distance supérieure à la distance focale ;
- vers la gauche de la lentille (⇒ formation d'une image virtuelle, non renversée) si l'objet est éloigné de la lentille par une distance inférieure à la distance focale (cas de la loupe).
L'illustration ci-dessous illustre ce second cas (et en outre l'observateur est positionné à la distance p de cette image virtuelle, ce qui signifie image net et cristallin contracté au maximum). L'image virtuelle est plus grande ... mais aussi plus éloignée que l'objet ⇒ son impression sur la rétine est-elle plus grande avec la loupe ? La réponse est affirmative, et l'illustration en montre la raison : la loupe a pour effet d'augmenter l'angle de vision (NB : celui-ci correspond à la pente de la réfraction du rayon incident parallèle à l'axe optique).
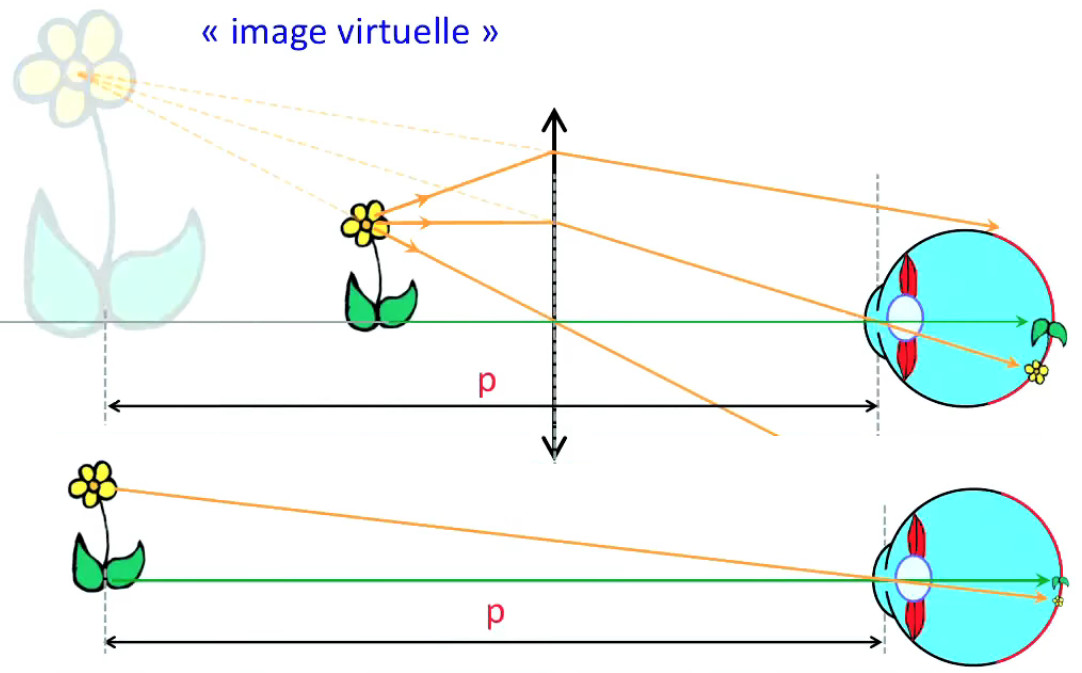
Or, étant donné que cet angle est inchangé par la position de l'objet, sa taille sur la rétine serait inchangée si on le modifiait sa position ... sauf que :
- si rapprochement ⇒ l'image ne serait plus nette puisqu'on serait alors en-dessous du p ;
- si éloignement ⇒ le cristallin pourrait être relâché puisqu'on serait alors au-delà du p.
NB : cette absence d'effet d'une modification de la distance sur la taille de l'image est du au cas particulier de l'illustration supra, qui est telle que la pupille est placée juste au niveau du foyer.
Qu'en est-il de la position particulière telle que l'objet est situé à distance focale de la loupe ? Nous avons vu que les rayons diffusés par un point situé à distance focale de la lentille sont réfractés par elle en rayons parallèles. Par conséquent l'image virtuelle est située à l'infini (et y est infiniment grande ... pour une taille inchangée sur la rétine).
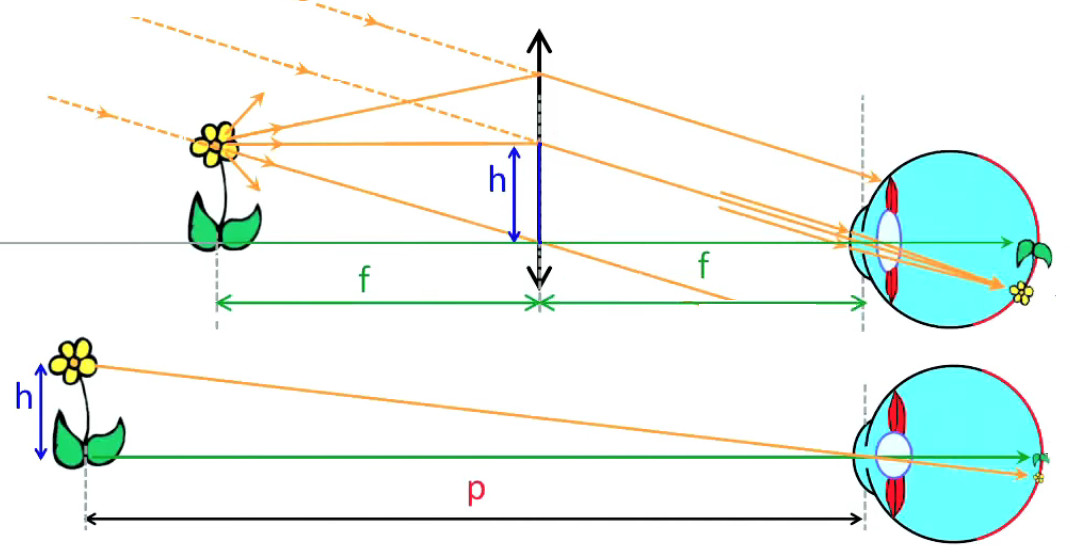

Or nous avons vu également que le cristallin est conçu pour être au repos lorsque les rayons lumineux qui le traversent sont parallèles entre eux. C'est là que réside l'intérêt de la loupe : situer le plan image au-delà du punctum proximum. Ainsi la position idéale d'une loupe est à distance focale de son support d'observation.
On appelle facteur de grossissement d'une loupe le rapport :
G = "angle de vision avec loupe" / "angle de vision sans loupe" ⇔
G = ( h / f ) / ( h / p ) ⇔
G = p / f
Ainsi une personne âgée dont p=50cm doit utiliser une loupe de focale f=5cm pour augmenter par dix la taille de l'objet observé.
NB : la distance focale f est une grandeur physique, tandis que le "punctum proximum" p est une grandeur biologique.
Enfin qu'en est-il si l'objet est placé à une distance supérieure à la distance focale de la lentille ? Dans ce cas il y a convergence vers la droite de la lentille, et donc formation d'une image réelle. Si celle-ci se situe entre le cristallin et la rétine ou après la rétine ⇒ son impression sur la rétine est floue car à un point de convergence correspondent plusieurs sur la rétine (cette situation est équivalente à la myopie, qui peut être corrigée par des lentilles divergentes).
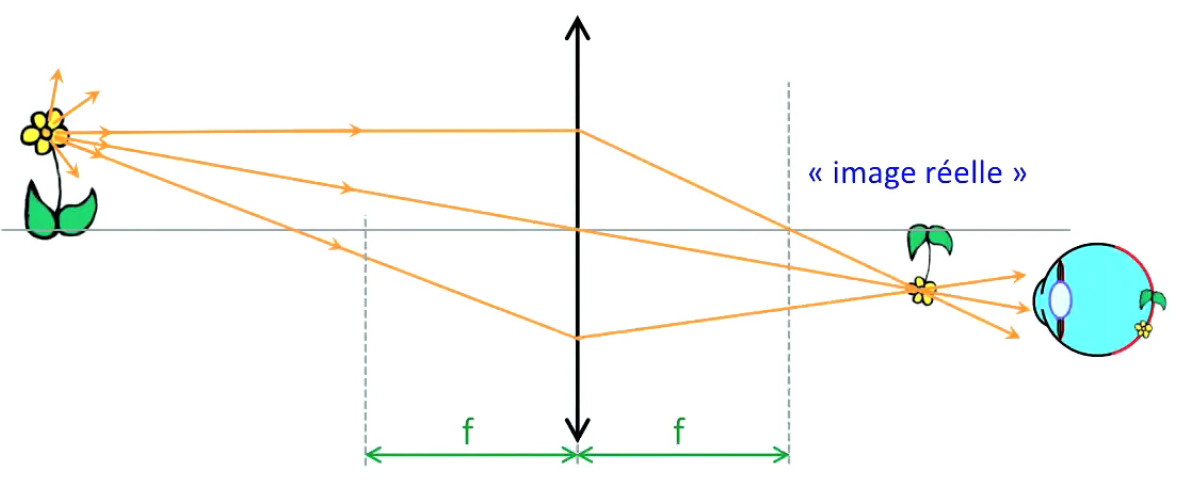
Relation de conjugaison des lentilles
Loi des lentilles. Soient les indices i pour "image" et o pour "objet", dans le graphique cartésien suivant, les couples de triangles équivalents montrent que :
yi / yo = xi / xo (formule du grandissement)
yi / yo = - ( xi - f ) / f
⇒
xi / xo = - xi / f + 1 ⇔
1 / xo = - 1 / f + 1 / xi ⇔
1 / xi - 1 / xo = 1 / f (relation de conjugaison)
Il s'agit de la conjugaison (taille et distance) entre points objet et image, qui sont dits "conjugués".
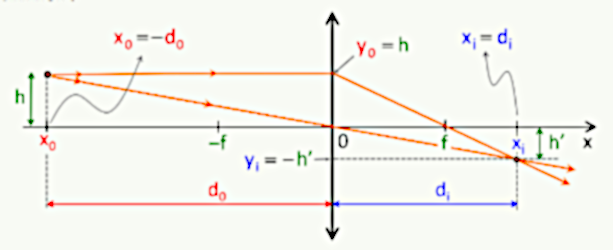
Quelques valeurs remarquables de la relation de conjugaison (et dont les valeurs son facilement vérifiables géométriquement) :
- si do = f alors di = ∞ : un objet dans le plan focal de la lentille a son image àl’infini ;
- si do < f alors di < 0 : cohérent avec le fait que (puisque do<f) la convergence se fait vers la gauche de la lentille (image virtuelle) ;
- si do = di alors do = di = 2 * f et l’image a la même taille que l’objet.
Si la distance séparant l'objet de la lentille est supérieure à 2*f, son image réfléchie par la lentille sera réduite, et inversement, tendra jusqu'à l'égalité au fur et à mesure que la distance objet (do) se rapprochera de 2f.
- si do = ∞ alors di = f : un objet à l’infini a son image dans le plan focal ;
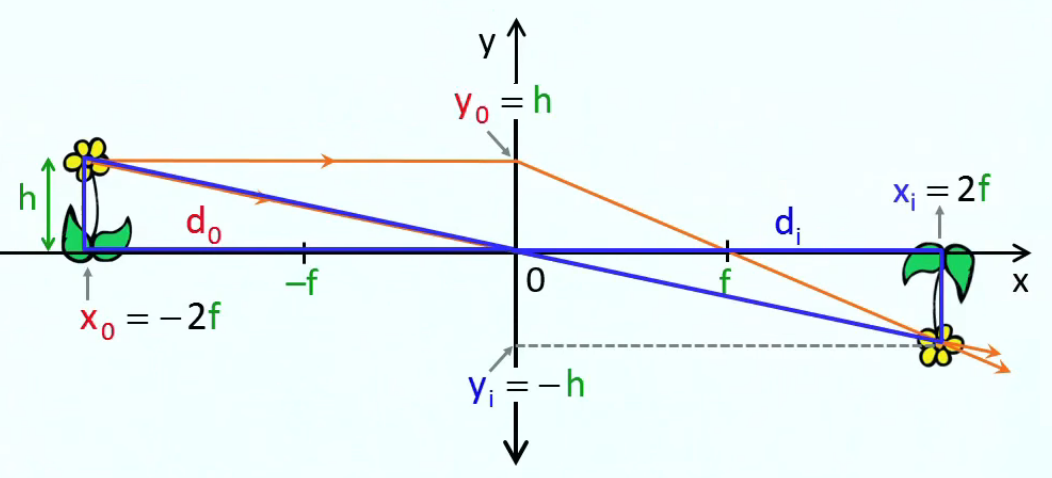
Lentille divergente
Lentille
divergente
La lentille sphérique divergente est plus épaisse en ses bords qu'en son centre, contrairement à la lentille convergente. La distance focale d'une lentille divergente est négative, et son foyer est virtuel car déterminé par la prolongation virtuelle des rayons et non par les rayons eux-mêmes.
Plan focal image d'une lentille
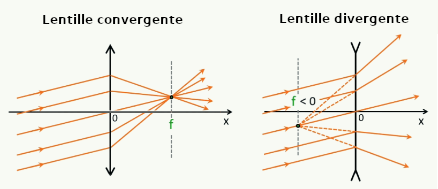
Notez l'inversion des flèches de l'axe vertical
Rappel. La notion de foyer correspond à des rayons incidents parallèles. Le foyer image (réel ou virtuel) est donc toujours l’image (réelle ou virtuelle) d’un point à l’infini sur l’axe optique. Enfin la distance focale f est définie comme la valeur de l’abscisse (x) du foyer image.

Le schéma suivant montre pourquoi l'image produite est plus petite que l'objet. Le lecteur pourra y vérifier facilement la cohérence avec la relation de conjugaison (302).
Il explique également l'effet d'optique illustré par la photo ci-contre : le foyer image est devant la lentille et l'image réduite se situe entre celle-ci et le foyer.
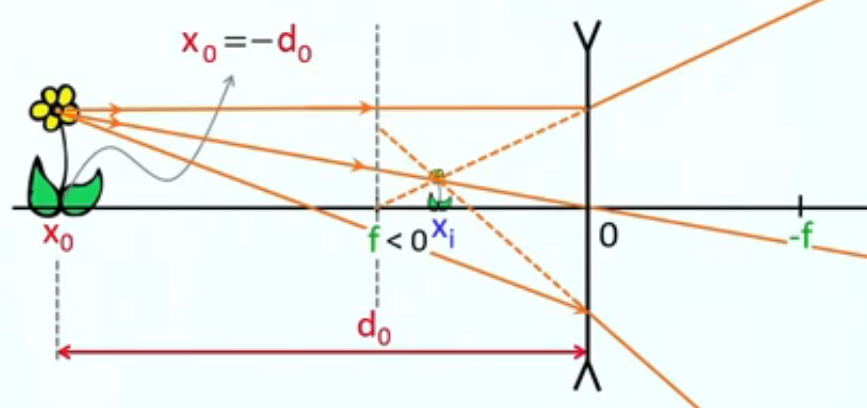
Par le même type de construction géométrique on pourra facilement vérifier que si xo = f < 0 alors xi = f / 2, et que ce résultat est cohérent avec la formule de grandissement (301).
Retour inverse. Si de la lumière est renvoyée sur elle-même, elle parcourt exactement le même rayon lumineux en sens contraire, y compris lorsqu’elle subit une réfraction. Cette propriété est la propriété de "retour inverse" de la lumière. Cette propriété est caractérisée par la notion de "foyer objet", dont le plan focal objet est symétrique au plan focal image c-à-d situé à une distance -f du centre de la lentille.
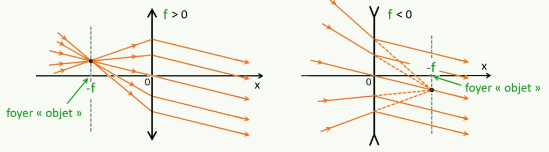
Le graphique ci-dessus montre que les rayons lumineux qui proviennent d’un point du plan focal objet d’une lentille (convergente ou divergente) en ressortent sous forme d’un faisceau de rayon parallèles entre eux. L’image de ce point se trouve à l’infini. Si la lentille est divergente, un tel objet doit être virtuel (non démontré ici).
Le tableau suivant synthétise les propriétés des lentilles divergentes et convergentes.
| Lentille convergente | Lentille divergente | |
|---|---|---|
| foyer image | réel (après) | virtuel (avant) |
| foyer objet | réel (avant) | virtuel (après) |
| distance focale | positive | négative |
La vision
Cette vidéo illustre les sections précédentes en expliquant le phénomène biologique de la vision (du seul point de vue de la physique, ainsi notamment les aspects neurologiques ne sont pas traités). C'est une excellente liaison avec le chapitre consacré à la biologie ...